Самый трудный параграф

Человеку нужны машины, а чтобы они работали, надо уметь создавать движение – двигать поршни, вращать колеса, тянуть вагоны поезда. Движение машин требует работы. Как получить ее?

Казалось бы, вопрос ясен: работа происходит за счет энергии. Надо отнять у тела или системы тел энергию – тогда получится работа.

Рецепт вполне правилен. Но как совершить такое превращение? Всегда ли возможно отобрать энергию у тела? Какие для этого нужны условия?

Мы сейчас увидим, что почти вся энергия, имеющаяся вокруг нас, совершенно бесполезна: она не может быть превращена в работу, и ее никак нельзя причислить к нашим энергетическим запасам. Разберемся в этом.

Отклоненный от положения равновесия маятник рано или поздно остановится; раскрученное рукой колесо перевернутого велосипеда сделает много оборотов, но в конце концов тоже прекратит движение. Нет никакого исключения из важного закона: все окружающие нас тела, приведенные в движение каким-либо толчком, в конце концов останавливаются.

Если имеется два тела, нагретое и холодное, то тепло будет передаваться от первого ко второму до тех пор, пока температура не уравняется. Тогда теплопередача прекратится, и состояния тел перестанут изменяться: установится тепловое равновесие.

Нет такого явления, при котором тела самопроизвольно выходили бы из состояния равновесия. Не может быть такого случая, чтобы колесо, сидящее на оси, начало бы вертеться само по себе. Не бывает и так, чтобы нагрелась сама по себе кастрюля с водой, поставленная на холодную, незажженную плиту.

Стремление к равновесию означает, что у событий имеется естественный ход: тепло переходит от горячего тела к холодному, но не может самопроизвольно перейти от холодного к горячему.

Механическая энергия колеблющегося маятника благодаря сопротивлению воздуха и трению в подвесе перейдет в тепло. Однако ни при каких условиях маятник не начнет раскачиваться за счет тепла, имеющегося в окружающей среде.

Тела приходят в состояние равновесия, но выйти из него не могут.

Этот важнейший закон природы (его называют вторым началом термодинамики) сразу же показывает, какая часть находящейся вокруг нас энергии совершенно бесполезна. Ею оказывается тепловое движение молекул тех тел, которые находятся в состоянии равновесия. Такие тела не способны превратить свою энергию в механическое движение.

«Мертвая» часть энергии огромна. Если понизить температуру килограмма земной породы на один градус, то он, имеющий теплоемкость 0,2 ккал/кг, потеряет 0,2 большой калории. Это относительно небольшая величина. Однако прикинем, какую энергию мы получили бы, если бы удалось охладить на тот же один градус весь земной шар, масса которого равна 6·10²⁴ килограммов. Умножая, мы получим 1,2·10²⁴ больших калорий. А это баснословная энергия: в настоящее время электроэнергия, вырабатываемая ежегодно электростанциями всего мира, равна 10¹⁵ – 10¹⁶ больших калорий, то есть в миллиард раз меньше.

Примирившись с тем, что нельзя предложить двигатель, создающий работу из ничего (так называемый вечный двигатель первого рода), и воодушевившись грандиозными числами, которые мы только что привели, горе-изобретатели взялись за конструирование двигателей, работающих за счет одного лишь охлаждения среды (так называемый вечный двигатель второго рода). Однако если водитель транспорта проехал на красный свет даже при минимальной скорости, ему не оправдаться тем, что он ехал с допустимой скоростью в 30 километров в час. Подчиняться надо обоим правилам.

То же относится и к конструкторам двигателей, которые попытались бы защитить свое создание ссылкой на то, что их идеи не противоречат закону сохранения энергии.

Этого мало! Утверждение, что система тел, находящихся при одной температуре, энергетически бесплодна, есть также закон природы.

Итак, для получения работы (то есть отнятия энергии) необходимо прежде всего нарушить тепловой покой. Для этого надо, в свою очередь, затратить энергию. Только тогда удастся осуществить процесс перехода тепла от одного тела к другому или превращения тепла в механическую энергию.

Создание потока энергии – вот необходимое условие получения работы. На «пути» этого потока возможно превращение энергии тел в работу.

Поэтому к энергетическим запасам, полезным для людей, относится энергия лишь «неуспокоившихся» тел.

Второе начало термодинамики, сущность которого мы изложили, фиксирует факты. Но каков внутренний смысл этого закона? Почему вся вселенная – это дорога к равновесному состоянию? Почему предоставленные самим себе тела неотвратимо приближаются к состоянию, когда механическое движение прекращается, а температуры тел уравниваются?

Вопрос этот очень важен и интересен. Кроме того, он труден, но мы подготовлены к ответу на него. Дело заключается в том, что равновесное состояние является наиболее вероятным.

Нам придется потратить одну-две странички на объяснение этой мысли. Прежде всего о самом слове «состояние». Оно употребляется в физике в двух смыслах. А чтобы между ними не путаться, введем два термина, которые несколько некрасивые и громоздкие, но, что поделаешь, зато научные и общепринятые. Итак, надо различать макросостояния тел и их микросостояния.

Термин «макросостояние» совпадает с житейским словом. Помните обычный утренний обмен фразами доктора и сестры в больнице?

– Каково состояние больного? – спрашивает врач.

– Без изменения, – отвечает сиделка, – температура та же, давление и пульс те же самые.

Макросостояние газа, жидкости или твердого тела характеризуются также в первую очередь температурой и давлением. Но, разумеется, теперь речь идет не о давлении крови, а о давлении, которое на тело оказывает окружение. Давление и температура – основные показатели, говорят – параметры, состояния. Если давление и температура не меняются, то с телом ничего не происходит, все свойства его сохраняются.

Другой подход необходим, если речь идет не о газе в баллоне, не о жидкости в сосуде и не о куске твердого тела, а о механической системе: машине, состоящей из множества рычагов и шестеренок, теперь макросостояние будет описано, если указать взаимное расположение частей механизма, а также скорости, с которыми эти части движутся.

Приходится, как видим, и в макросостояниях различать два вида состояний – термодинамическое и механическое. И описываются они разными параметрами.

До того как молекулы вышли на сцену, эти два варианта описания казались совершенно не связанными. Относились они к разным случаям: одно к покоящейся жидкости или газу, другое – к механическим устройствам и ничего общего друг с другом не имели. Параметры, употребительные в термодинамике, – это давление и температура, механические параметры – это координаты и скорости. И одно к другому никогда не сводилось.

Перевод термодинамики на молекулярный язык сразу же выявил наличие мостика между этими двумя описаниями. С точки зрения молекулярной гипотезы всякое тело есть система взаимодействующих молекул, то есть не что иное, как механическая система, нечто вроде рычагов и шестеренок. А состояние такой системы задается, как мы только что видели, взаимным расположением и скоростями ее частей – в нашем случае молекул. Что же, оказывается, дело обстоит не так уж сложно? Термодинамическое макросостояние есть не что иное, как механическое состояние системы молекул?

Осторожнее, повременим с таким заключением. Если немного подумать, то станет ясно, что дело обстоит не так уж просто.

В термостате стоит стакан с жидкостью. Ее температура и давление неизменны. Термодинамическое состояние ее в каждое мгновение одно и то же. Кажется, она – само постоянство и покой. Но ведь молекулы этой жидкости совершают свой вечный тепловой танец! Значит, механические состояния молекул, которые образуют эту самую жидкость, меняются каждое мгновение! Значит, постоянство и покой обманчивы и жидкость живет бурной жизнью?!

Раз уж механическое состояние системы молекул, составляющих жидкость, не отражает ее «макроскопического спокойствия», то назовем его иначе: термин – «микросостояние» будет подходящим по смыслу дела. Теперь мы скажем: каждое состояние (макросостояние) осуществляется беспрерывной сменой огромного числа микросостояний.

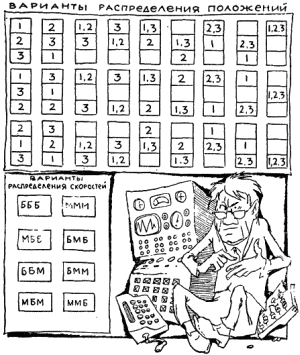
Представьте себе, что система состоит из трех перенумерованных молекул. Микросостояние системы будем описывать донельзя грубо, а именно, поделим сосуд, в котором носятся эти три молекулы, на три отсека, а что касается скорости, то разобьем их на две группы – до 1 км/сек (малая скорость) и больше 1 км/сек. Каково будет число микросостояний в этом смехотворно простом случае? Считайте, 8 вариантов распределения скоростей и 27 вариантов положений, то есть 27?8! = 216 микросостояний для модели газа, упрощенной до смешного!

Нетрудно понять, что в реальных случаях, когда для характеристики системы требуется задать точно месторасположение и скорости миллиарда миллиардов молекул, числа микросостояний, относящиеся к одному макросостоянию, становятся непредставимо большими.

В маленьком газовом баллончике модной зажигалки носятся молекулы газа, который зовется пропаном. Каждое мгновение расположение молекул и их скорости меняются, каждое мгновение – другое микросостояние.

Но хотя число микросостояний огромно, оно все же не бесконечно велико. Физики могут сосчитать число микросостояний в баллончике зажигалки. Так как мне неизвестны технические параметры этой зажигалки, то я могу сообщить лишь порядок интересующей нас величины. Число микросостояний в баллончике записывается 10¹⁷ цифрами!!! Число печатных знаков в книжке, которую вы читаете, меньше миллиона (10⁶). Значит, чтобы записать интересующее нас число микросостояний, потребовалась бы книга в сто миллиардов раз (10¹¹) более толстая, чем эта.

Надеюсь, что мне удалось поразить ваше воображение, но моя задача не в этом. Цель этого самого трудного параграфа – показать фундаментальную роль теории вероятностей в учении о равновесии тел. К этой цели мы приблизились вплотную, но, чтобы вы отдохнули, мне хочется разрешить себе немного пофилософствовать на тему о трудности популярного изложения научных истин.

В какой бы форме нам ни преподносилось научно-популярное сочинение, оно всегда будет представлять собой рассказ о научных фактах и идеях.

Разговор может идти в двух тональностях. Первая возникает тогда, когда автор ставит перед собой задачу дать ответ на вопросы «как?»; вторая – в тех случаях, когда предстоит ответить на вопросы «почему?».

Различие между этими двумя вариантами изложения научных истин велико. В первом – задача литератора состоит в том, чтобы вести неторопливый рассказ, не забыть важные детали, заботиться об образности изложения, прибегать к повторениям, заставляя этим читателя держать перед глазами всю картину события. Нет проблемы такой степени сложности, чтобы ее нельзя было осветить ответами на вопросы «как сделано?», «как построено?», «как работает?»… на любом уровне подготовки читателя.

Во втором случае задача совсем другая. Дать ответ на вопрос «почему?», значит показать, что некое событие или идея вытекают из других положений более общего характера. Но показать, что частное следует из общего, можно лишь методами логики, а еще лучше – методами математики.

Задача литератора, вступившего на тяжелый путь ответов на вопросы «почему?», неизмеримо сложнее трудностей, с которыми сталкивается автор, описывающий ледники Кавказских гор или устройство моторного катера с новыми обводами. Ему надо тщательно выделить аксиомы, лежащие в основе объяснения, уменьшить для облегчения восприятия высоту логических ступеней, ведущих от основания к вершине объяснения.

Чтобы объяснение «дошло», читатель должен держать в памяти одновременно все логические переходы, и каждый из них должен быть настолько ясным, чтобы казаться само собой разумеющимся.

Поэтому-то тяжело приходится и автору и читателю.

Подобные трудности возникают и при рассказе о применении теории вероятностей к исследованиям газов.

Напоминаем, что макросостояние тела реализуется беспрерывно меняющимися микросостояниями. Число различных микросостояний огромно, но вычислять его физики умеют. Как это нужно делать, показал Людвиг Больцман.

А зачем нужно знать эти числа, которые нельзя записать цифрами, даже истратив на это все мировые запасы бумаги? Какой смысл они имеют?

Если вы внимательно прочитали предыдущие части книги, то вы сами поспешите с ответом. То, что число способов осуществления того или иного результата события пропорционально вероятности результата, вы знаете, не правда ли? А теперь мы выяснили, что число микросостояний есть число способов реализации макросостояния.

По законам логики из этих двух позиций железно следует, что число микросостояний пропорционально вероятности макросостояния.

Вероятность состояния… Как понять сочетание этих двух слов? В самом прямом смысле. Как всегда, вероятности познаются в сравнении. Что вероятнее: стакан горячего чая с лежащим на дне куском сахара или стакан горячего чая с растворившимся в нем сахаром? Что вероятнее: раскаленный кусок железа, лежащий на земле, или кусок железа, принявший температуру почвы?

Слишком простые вопросы, скажет читатель. Согласен. Но сумели бы вы на них ответить без помощи теоремы Больцмана, которую мы сейчас разъясняем? Оказывается, переход к равновесию является дорогой к наиболее вероятному состоянию.

Мне остается убедить вас в том, что вероятность состояния (равная числу микросостояний, которыми она осуществляется) действительно достигает максимума при равновесии.

Попробуем прийти к этому выводу с помощью аналогии. Раскроем книгу на странице 68 [ссылка] и вспомним смысл чисел, образующих тридцатую строку чудесного треугольника Паскаля. Напоминаю, что каждое число показывает, сколькими комбинациями можно прийти к одному макроскопическому результату, к одному состоянию. Общее число бросков рулеточного шарика равно 30. Поэтому макросостояние в тридцать «красных» (начало строки) осуществляется 1 способом, двадцать девять «красных» и один «черный» (следующее число строки) – 30 способами, двадцать восемь «красных» и два «черных» (третье число строки) – 435 способами… 15 «красных» и 15 «черных» (середина строки) – 155 117 520 способами. Разные способы осуществления одного и того же результата (то есть одного и того же отношения «черного» и «красного»), но отличающиеся лишь разным порядком их выхода, – превосходные аналоги макросостояния.

Каковы признаки наиболее вероятного макросостояния? Примерно равное количество «красного» и «черного», отсутствие преимущества того или другого цвета, наибольший беспорядок. Действительно, можно сказать: наиболее беспорядочными являются те серии бросков, что в середине строки, то есть те случаи, когда «черное» и «красное» подравниваются. Упорядоченными сериями являются такие, в которых наблюдается большой перевес одного цвета. Полный порядок – это одноцветная серия. Треугольник Паскаля показывает, что беспорядочные серии встречаются много чаще упорядоченных. Нетрудно понять, распространив этот вывод на мир молекул, для изображения которого с помощью треугольника Паскаля потребовалось бы число его строк довести до миллиарда миллиардов, что вероятности беспорядочных серий будут в невообразимое число раз превосходить вероятность порядка.

Аналогия, конечно, не всегда совершенный способ доказательства, но все же я надеюсь, что эти выводы читатель примет без внутреннего протеста. Для системы молекул беспорядок означает отсутствие особенных направлений движения, отсутствие особых мест скопления молекул, отсутствие каких-либо часто встречающихся скоростей. На языке рулетки это и значит – примерно равное число «черного» и «красного».

Из нашей аналогии следует далее, что неравновесное состояние является менее вероятным. Раз оно неравновесно, то в нем нарушены устойчивые пропорции быстрых и медленных молекул, плотность неоднородна по объему, имеются преимущественные направления движения молекул… То есть «черного» много больше, чем «красного».

Несколько страниц назад я принялся разъяснять фразу: «равновесное состояние является наиболее вероятным». Надеюсь, что я справился с этой задачей. Мы увидели, что наблюдаемое состояние тела осуществляется огромным числом микросостояний; выяснили, что число микросостояний пропорционально вероятности макросостояний; методом аналогии показали, что вероятность состояния возрастает с беспорядком в расположении и движении частиц. Из всего этого по законам логики мы пришли к этой действительно емкой фразе, усвоение которой, я боюсь, потребовало от читателя некоторого напряжения.

В студенческие годы мне попала в руки толстая книга в ярко-синем переплете, изданная в Томске. Это был курс термодинамики. В предисловии автор писал:

«Хочу предупредить учащихся о том, что понятие энтропии усваивается с большим трудом. Я лично понял, что такое энтропия, примерно после двадцати лет педагогической деятельности».

Я помню, как изумила меня наивная и откровенная скромность автора.

Содержание только что прочитанного параграфа приведет нас, как вы сейчас увидите, к понятию энтропии. Так что, если вам было трудно, не удивляйтесь.