ДРУГИЕ АРИФМЕТИЧЕСКИЕ РАБОТЫ
ДРУГИЕ АРИФМЕТИЧЕСКИЕ РАБОТЫ
ДЕЛИМОСТЬ НА СЕМЬ [10]
Мистер Эскью в письме №1274 от 30 мая спрашивает о доказательстве метода установления делимости числа на семь, которое, как он утверждает, открыто мистером Рикардом из Бирмингема. Оно, возможно, многими открыто; к примеру, моим отцом, который обучил меня ему лет тридцать назад. Проверочное число одинаково полезно для 7, 11 и 13. Метод, разработанный моим отцом, даёт, в случае делимости числа на все эти три величины, также ещё одну величину без дальнейшего труда; и в этом отношении он имеет преимущество перед методом мистера Рикарда.
Если некое число N разметить, начиная с правого конца, на периоды в три разряда, обозначив эти периоды через a, b, c и т. д., и если M будет разницей между суммами перемежающихся периодов, то получим, записывая r вместо 1000,
N = a + br + cr + dr + и т. д.
M = a – b + c – d + и т. д.
Тогда
N – M = b(r + 1) + c(r2 – 1) + d(r3 + 1) + и т. д.
и делимо на (r + 1); следовательно, если M делимо на (r + 1) или на какой-либо его множитель, то так же и N. И в этом случае r + 1 = 1001 = 7 ? 11 ? 13.
Правило моего отца состояло в том, чтобы поместить самый правый период под следующим и произвести вычитание, поместив остаток вновь под следующим периодом и так далее. В последнем периоде вычитание производится вверх ногами, если нижнее число окажется большим. В нашем примере, поскольку мы имеем 1, которая переносится в последний период, число 931 следует читать как 932. Конечный остаток, 924, есть наше проверочное число, и поскольку оно делимо на 7 и на 11, то исходное число также на них делится.
Если случится так, что проверочное число окажется равным нулю, то вторая строка сделается частным от деления данного числа на 1001, то есть множителем, остающимся после сокращения на 7, на 11 и на 13. В самом деле, обозначим вторую строку через V; приписывая в конце три нуля, получаем 1000V; а мы знаем, что если вычесть её из верхней строки, то остатком будет V. Следовательно, N = 1001V = 7 ? 11 ? 13 ? V. Если бы в вышеприведённом примере крайний левый разряд составлял 932 вместо 8, то проверочное число оказалось бы нулём.
Если такие периоды составить из единичных разрядов, то есть если r = 10, мы получаем критерий делимости на 11 и в то же самое время частное после сокращения на 11. Изложенное правило требует поместить последнюю цифру под соседней, вычесть, разность поместить под следующей и так далее. В нашем примере проверочное число равняется нулю; следовательно, данное число — это 11 ? 5852053.
С периодами по два разряда мы получаем критерий делимости на 101; то же для четырёх или более разрядов.
Ч. Л. Доджсон
К. Ч., Оксфорд
P. S. Сумма всех периодов даёт нам, для периодов из 1, 2, 3 и т. д., разрядов, критерий делимости на 9, 99, 999 (= 27 ? 37) и т. д., или для любого множителя этих чисел. Для этого метода также можно выработать правило, аналогичное вышеизложенному; например, для критерия в отношении 999 размечаем на периоды по три, пишем 000 поверх крайнего правого периода и вычитаем, записывая разность поверх следующего и так далее. Следовательно, если так же случится, что проверочное число обратится в нуль, верхняя строка (за опусканием 000) станет частным от деления данного числа на 999.
Вероятно, похожие правила можно выработать для большинства простых чисел. Я сам разработал достаточно простые правила для 17 и 19, но подобные процедуры скорее любопытны, чем удобны.
НАЙТИ ДЕНЬ НЕДЕЛИ ДЛЯ ЛЮБОЙ ЗАДАННОЙ ДАТЫ [11]
Натолкнувшись на следующий способ вычисления в уме дня недели для любой заданной даты, шлю его Вам в надежде, что он заинтересует некоторых из Ваших читателей. Сам я считаю медленно; и поскольку, как я обнаружил, среднее время, затрачиваемое мной на решение всех таких задач, составляет двадцать секунд, то для тех, кто считает быстро, хватит, несомненно, и пятнадцати.
Берём заданную дату четырьмя частями, а именно: количество сотен, количество лет сверх, месяц, день.
Вычисляем следующие четыре величины, прибавляя каждую, по её нахождении, к общей сумме предыдущих величин. Если какая-то величина либо такой итог превышает 7, делим на 7 и сохраняем один лишь остаток.
Член «сотни». — Для старого стиля (который закончился 2 сентября 1752 года), вычитаем из 18. Для нового стиля (который начался 14 сентября [того же года] [12]) делим на 4, избыток отнимаем у 3, оставшееся умножаем на 2.
Член «годы». — Складываем вместе количество дюжин, избыток и количество четвёрок в избытке.
Член «месяц». — Если он начинается либо заканчивается на гласную, вычитаем число, обозначающее его номер в году, из 10. Результат плюс количество дней в нём дают член следующего месяца. Значение для января есть «0», для февраля или марта (третий месяц) будет «3», для декабря (двенадцатый месяц) будет «12».
Член «день» есть число месяца.
Полученный таким образом итог нужно подправить вычитанием «1» (но сперва добавив «7», если итог равен «0»), если дата приходится на январь или февраль високосного года; следует помнить, что всякий год, делящийся на 4, будет високосным, за исключением лишь тех сотенных лет для нового стиля, когда количество сотен не делится на 4 (например, 1800-й год).
Окончательный итог даёт день недели, причём «0» означает воскресенье, «1» — понедельник и так далее.
ПРИМЕРЫ
18 сентября 1783 года
17, делённое на 4, оставляет «1» сверх; 1 из 3 даёт «2»; дважды 2 будет «4».
83 есть 6 дюжин и 11, что даёт 17; плюс 2 будет 19, т. е. (после деления на 7) «5». В итоге 9, т. е. «2».
Член для августа есть «8 от 10», т. е. «2», а потому, для сентября, он есть «2 плюс 31», т. е. «5». В итоге 7, т. е. «0», который выходит.
18 даёт «4». Ответ: четверг.
23 февраля 1676 года
16 из 18 даёт «2».
76 есть 6 дюжин и 4, что даёт 10; плюс 1 будет 11, т. е. «4». В итоге «6».
Член для февраля есть «3». В итоге 9, т. е. «2».
23 даёт 2. В итоге «4».
Поправка для високосного года даёт «3». Ответ: среда.
Льюис Кэрролл [13]
ПРАВИЛО НАХОЖДЕНИЯ ДАТЫ ПАСХИ ДЛЯ ЛЮБОГО ГОДА ВПЛОТЬ ДО 2499
1. Введение
В основе данного Правила лежит формула Гаусса; Гауссово доказательство этой формулы приведено во втором томе «Monatliche Correspondenz» Цаха (август 1800 года, страницы 221—230), по каковой публикации эту формулу воспроизвёл мистер У. У. Роуз Болл в своих «Математических <эссе и> развлечениях», выпущенных издательством «Макмиллан и Ко» [14]. Единственная отличительная черта моей версии данного Правила состоит в его большей простоте. Моим способом результат может быть посчитан в уме, без особого труда, за полминуты; метод же Гаусса определённо потребовал бы гораздо большего времени, как и гораздо больших усилий при вычислении в уме.
Перед тем, как приступить к самому Правилу, читателю следует овладеть кое-какими необходимыми арифметическими процедурами, изложенными здесь же.
2. Некоторые необходимые арифметические процедуры
(1)
Прибавить 15 к данному числу. Производится в два шага—10 и 5.
{Так, если дано число 187, то говорим: «197, 202».}
(2)
Найти Остаток, получающийся от деления данного числа на 4.Делим<на 4 лишь>две последние цифры.
(3)
Найти Остаток, получающийся от деления данного числа на 7. Называем следующие одно за другим делимые. Это всё, чего требует наш монолог про себя. Остаток от каждого делимого (который, разумеется, служит десятковым порядком при следующем делимом) находится непосредственно.
{Так, если дано число 4325, то говорим: «43, 12, 55; 6».} [15]
Будет лучше изгнать семёрки, где только удобно так поступить.
{Следовательно, если делимое будет кратным семи, говорим «выходит» и пропускаем его. Так, если дано число 4225, то говорим: «42 выходит, 25; 4». Если дано число 4769, говорим: «47, 56 выходит, 9; 2».}
(4)
Найти остаток, получающийся от деления данного числа на 19. Если наше число не превышает 30, остаток находится непосредственно. Если число превышает 30, берём столько его цифр, сколько образуют число, превышающее единицу. Если это число чётное, делим его пополам и складываем со следующей цифрой; если оно нечётное, берём его меньшую половину и складываем со следующей цифрой, приставив к ней спереди единицу. Мысленно подставляем результат на место использованных таким образом цифр и продолжаем как ранее.
{Так, если дано число 88, то говорим: «4 и 8 будет 12». Если число 98, говорим: «4 и 18 будет 22; 3». Если число 147, говорим: «7 и 7 будет 14». Если число 157, говорим: «7 и 17 будет 24; 5». Если число 687, говорим: «3 и 8 будет 11; 5 и 17 будет 22; 3».}
Изгоняем девятнадцатки, где только можно.
{Так, если дано число 1992, пропускаем первые две цифры и говорим: «4 и 12 будет 16». Если число 5749, говорим: «2 и 17 будет 19, которое выходит; 2 и 9 будет 11». Если число 998, говорим: «4 и 19 будет 4; 2 и 8 будет 10». Если число 7994, говорим: «3 и 19 будет 3; 1 и 19 будет 1; 14».}
Если требуется прибавить 18, либо 17 и т. д., именуем их как «19 минус 1», либо «19 минус 2» и т. д. и пропускаем это «19».
{Так, если дано число 789, то говорим: «3 и минус 1 будет 2; 1 и 9 будет 10». Если число 967, говорим: «4 и минус 3 будет 1;17».}
Но этим способом не следует пользоваться, если число, к которому нужно прибавить 18 и т. д., меньше числа, которое предстоит вычесть.
{Так, если дано число 567, то не говорим: «2 и минус 3», но говорим: «2 и 16 будет 18; 9 и 7 будет 16».}
(5)
Помножить данное двузначное число, сумма цифр которого не превышает 9, на 11. <Ответ находится> подстановкой суммы этих цифр между ними же.
(6)
Найти дефект данного числа от наименьшего кратного 30, которое содержит это число [16].
Данное число может быть (?) кратным 30, либо (?) отличаться от наименьшего кратного 30, которое содержит это число, не более чем на 10, либо (?) отличаться от него более чем на 10.
В случае (?) либо в случае (?) дефект усматривается непосредственно.
{Так, если дано число 180, то говорим: «дефект равен 0».Если число 203, говорим: «дефект равен 7».}
В случае (?) берём избыток данного числа сверх следующего меньшего кратного 30 и вычитаем из 30.
{Так, если дано число 189, то говорим: «9 сверх; дефект равен 21».Если число 192, говорим: «12 сверх; дефект равен 18».}
3. Правило нахождение дня Пасхи для любого нужного года вплоть до 2499.
Выражение «4-Rem», используемое в отношении определённого числа, означает «остаток, получающийся от деления этого числа на 4»; аналогично в случае выражений «7-Rem» и «19-Rem» [17].
Нам потребуются три числа, два из которых, коль скоро нужный год указан,известны на память; третье подлежит вычислению. Назовём эти числа a, h, k.
Наше Правило удобно разделить на три следующие части.
(1) Называем нужный год и затем вспоминаем по памяти величины a и h, к нему относящиеся. Для старого стиля эти величины всегда равны 15 и 6. Для нового стиля они даны в следующей таблице:
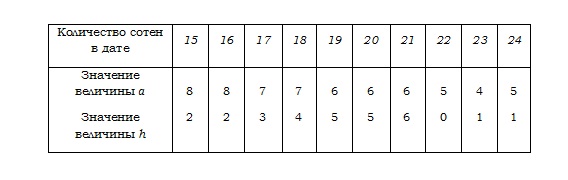
Мысленно представляем себе эту таблицу и проговариваем количества сотен, пока не доходим до нужного; затем называем значения a и h в каждом столбце.
{Так, если нужен 1582 г. (что, для нашей настоящей цели, будет по ст. ст., поскольку н. ст. не вступает ранее октября [18]), то говорим: «1582; ст. ст.; a и h суть 15 и 6».
Если нужен 1583 г. н. ст., говорим: «1583; н. ст.; 15; a и h суть 8 и 2».
Если дата — это 1583 г. ст. ст., говорим: «1583; ст. ст.; a и h суть 15 и 6».
Если дата — это 1948 г. н. ст., говорим: «1948; н. ст.; 15, 16, 17, 18, 19; a и h суть 6 и 5».}
(2) Опять же, называем нужный год и находим его 4-Rem и 7-Rem; затем берём «4-Rem плюс дважды 7-Rem», удваиваем, прибавляем h; 7-Rem от этого результата будет k.
{Так, если нужен 1582 г., то говорим: «1582; 4-Rem; 82; 2; 7-Rem; 15, 18, 42; 0; 2 и 0 будет 2; 4 и 6 будет 10; k равно 3».
Если нужен 1583 г. н. ст., говорим: «1583; 4-Rem; 83; 3; 7-Rem; 15, 18, 43; 1; 3 и 2 будет 5; 10 и 2 будет 12; k равно 5». Если это 1583 г. ст. ст., говорим: «1583; 4-Rem; 83; 3; 7-Rem; 15, 18, 43; 1; 3 и 2 будет 5; 10 и 6 будет 16; k равно 2».
Если нужен 1948 г. н. ст., говорим: «1948; 4-Rem; 48; 0; 7-Rem; 19, 54, 58; 2; 0 и 4 будет 4; 8 и 5 будет 13; k равно 6».
Если нужен 1948 г. ст. ст.. говорим: «1948; 4-Rem; 48; 0; 7-Rem; 19, 54, 58; 2; 0 и 4 будет 4; 8 и 6 будет 14; k равно 0».}
(3) Называем a и k; называем нужный год; находим его 19-Rem; умножаем на 11; прибавляем a; находим дефект результата от наименьшего кратного 30, которое его содержит; находим наибольшее кратное 7, содержащееся в дефекте и прибавляем k. Если результат не дотягивает до дефекта, то либо вычитаем 2 и называем апрель, либо (если этого нельзя сделать) прибавляем 29 и называем март. Если этот результат дотягивает до дефекта, то либо вычитаем 9 и называем апрель, либо (если этого сделать нельзя) прибавляем 22 и называем март.
{Так, если нужен 1582 г., и если известно, что a и k суть 15 и 3, то говорим: «a и k суть 15 и 3; 1582; 7 и минус 1 будет 6; 3 и 2 будет 5; 55 и 15 будет 65, 70; 10 сверху; дефект равен 20; 14 и 3 будет 17, что не дотягивает; вычитаем 2; 15 апреля».
Если нужен 1583 г. н. ст., и если известно, что a и k суть 8 и 5, говорим: «a и k суть 8 и 5; 1583; 7 и минус 1 будет 6; 3 и 3 будет 6; 66 и 8 будет 74; 14 сверху; дефект равен 16; 14 и 5 будет 19, что дотягивает; вычитаем 9; 10 апреля».
Если нужен 1583 г. ст. ст., и если известно, что a и k суть 15 и 2, говорим: «a и k суть 15 и 2; 1583; 7 и минус 1 будет 6; 3 и 3 будет 6; 66 и 15 будет 76, 81; дефект равен 9; 7 и 2 будет 9, что дотягивает; прибавляем 22; 31 марта».
Если нужен 1948 г. н. ст., и если известно, что a и k суть 6 и 6, говорим: «a и k суть 6 и 6; 1848; 9 и минус 5 будет 4; 2 и 8 будет 10; 110 и 6 будет 116; дефект равен 4; 0 и 6 будет 6, что дотягивает; прибавляем 22; 28 марта».
Если нужен 1948 г. ст. ст., и если известно, что a и k суть 15 и 0, говорим: «a и k суть 15 и 0; 1948; 9 и минус 5 будет 4; 2 и 8 будет 10; 110 и 15 будет 120, 125; 5 сверху; дефект равен 25; 21 и 0 будет 21, что не дотягивает; вычитаем 2; 19 апреля».} [19]
4. В облегчение запоминания
(1)
Запомнить нужный год, пока считаем согласно нашему Правилу. Если вы уверенно образуете мнемонические словечки, то найдёте, что это — весьма полезный способ. В противном случае нужный год вам лучше будет записать, поскольку для душевного спокойствия окажется сущим испытанием обнаружить, что, пока вы сосредоточенно выясняли дату Пасхи, тот год, для которого вы её высчитывали, выпал из вашей памяти!
{Годы, выбранные для примеров в следующем разделе, удобно запомнить посредством следующих слов: 853 «kilt», 1654 «box-leaf», 1881 «chokeboy» [20].}
(2)
Запомнить таблицу значений a и h.Первые шесть колонок — наиболее часто используемые. В отношении их заметим, что значения для a суть «две восьмёрки, две семёрки, две шестёрки» и что в первых трёх колонках a и h в сумме дают 10, а в следующих трёх 11.
Для последних четырёх колонок значения a и h даются в третьей и четвёртой строках следующей мнемонической строфы:
List my song to!
’Tis as wrong to
Save a flea
As rob a bee. [21]
Значения для текущего столетия, то есть 7 и 4, лучше будет накрепко отложить в памяти отдельной статьёй.
Запомнить значение k <до той минуты>, пока оно не понадобится. Это легко проделать с помощью руки. Для «0» держим ладонь раскрытой, для «1» сгибаем указательный палец и кладём на него большой, аналогичным образом для «2», «3» и «4»; для «5» сгибаем большой палец, а остальные кладём на него; для «6» сжимаем кулак, большой палец при этом отставив.
(3)
Если в процессе расчёта по второй части нашего Правила окажется, что «4-Rem плюс дважды 7-Rem» кратно 7, то k станет равным h; тогда сразу переходим к третьей части.
{Так, если нужен 1731 г. н. ст., то говорим: «15, 16, 17, a и h суть 7 и 3; 1731; 8 и минус 6 будет 2; 22 и 7 будет 29; дефект равен 1; 0 и 3 будет 3, что дотягивает; прибавляем 22; 25 марта».} [22]
(4)
Есть одна дата (и только одна, насколько мне известно), в отношении которой данное Правило не срабатывает. В 1954 году по новому стилю Пасха приходится на 18 апреля; настоящее же Правило даёт 25-е. Совершенно не могу объяснить этого весьма любопытного отклонения [23].
5. Примеры для образца
(1)
Год 853.
«Старый стиль; a и h суть 15 и 6; 4-Rem; 53, 5, 13; 1; 7-Rem; 853; 8, 5, 13; 6; 1 и 12 будет 13; 26 и 6 будет 32; k равно 4.
a и k суть 15 и 4; 853; 4 и 5 будет 9; 4 и 13 будет 17; 187 и 15 будет 197, 202; дефект равен 8; 7 и 4 будет 11, что дотягивает; вычитаем 9; 2 апреля».
(2)
Год 1654 (н. ст.)
«15, 16; a и h суть 8 и 2; 4-Rem; 54, 5, 14; 2; 7-Rem; 1654; 16, 25, 44; 2; 2 и 4 будет 6; 12 и 2 будет 14; k равно 0.
a и h суть 8 и 0; 1654; 8 и 5 будет 13; 6 и минус 5 будет 1; 11 и 8 будет 19; дефект равен 11; 7 и 0 будет 7, что не дотягивает; вычитаем 2; 5 апреля».
(3)
Год 1654 (ст. ст.)
«Старый стиль; a и h суть 15 и 6; 4-Rem; 54, 5, 14; 2; 7-Rem; 1654; 16, 25, 44; 2; 2 и 4 будет 6; 12 и 6 будет 18; k равно 4.
a и k суть 15 и 4; 1654; 8 и 5 будет 13; 6 и минус 5 будет 1; 11 и 15 будет 26; дефект равен 4; 0 и 4 будет 4, что дотягивает; прибавляем 22; 26 марта».
(4)
Год 1881 (н. ст.)
«a и h суть 7 и 4; 4-Rem; 81; 1; 7-Rem; 1881; 18, 48, 61; 5; 1 и 10 будет 11; 22 и 4 будет 26; k равно 5.
a и h суть 7 и 5; 1881; 9 и 8 будет 17; 8 и 11 будет 19; 0 и 7 будет 7; дефект равен 23; 21 и 5 будет 26, что дотягивает; вычитаем 9; 17 апреля».
(5)
Год 1881 (ст. ст.)
«a и h суть 15 и 6; 4-Rem; 81; 1; 7-Rem; 1881; 18, 48, 61; 5; 1 и 10 будет 11; 22 и 6 будет 28; k равно 0.
a и k суть 15 и 0; 1881; 9 и 8 будет 17; 8 и 11 будет 19; 0 и 15 будет 15; дефект равен 15; 14 и 0 будет 14, что не дотягивает; вычитаем 2; 12 апреля».
6. Примеры для упражнения
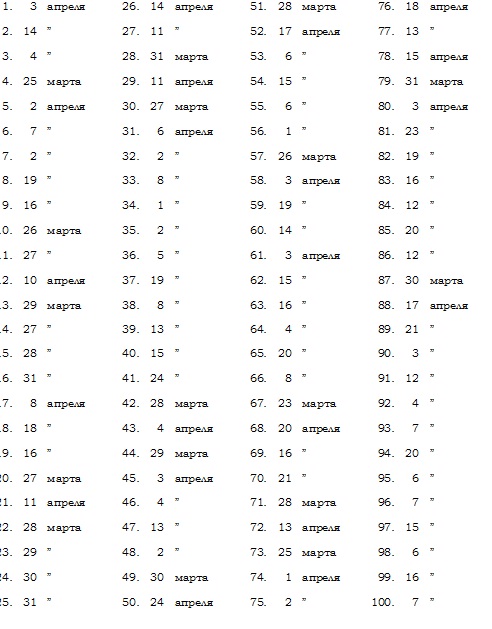
Для того из читателей, кто не обладает «Календарной книгой» профессора Де Моргана, ниже приведены сто различных дат, на которых он может поупражняться; ответы помещены в следующем разделе.
7. Ответы
