CURIOSA MATHEMATICA, ЧАСТЬ III КНИГА II Короткие способы выполнения некоторых арифметических процедур
CURIOSA MATHEMATICA, ЧАСТЬ III
КНИГА II
Короткие способы выполнения некоторых арифметических процедур
Глава 1. УМНОЖЕНИЕ ДЛИННЫХ ЧИСЕЛ
Основная идея данного способа пришла мне в голову 19 сентября 1879 года. Я размышлял над большим неудобством, возникающим при обычной процедуре умножения в столбик из-за того, что две цифры, которые требуется перемножить, часто находятся друг от друга на большом расстоянии, и о том преимуществе, каким стала бы возможность записать задачу так, чтобы все такие цифры оказывались стоящими рядом. Тогда и появилась счастливая мысль, что если написать меньшее число задом наперёд и передвигать его поверх другого числа вдоль него, то на каждом этапе такого смещения мы получим наблюдаемый непосредственно набор из пар цифр, чьи произведения потребуется только сложить друг с другом, чтобы получить единственный столбец для действия над ним уже как обычно [1].
Способ, который я вывел из этой идеи, может быть изложен следующим образом.
Записать два данных числа так, чтобы меньшее, если они неравной длины, располагалось над большим, а их разряды единиц были совмещены по вертикали. Провести под нашими числами черту. На отдельной полоске бумаги записать верхнее число задом наперёд, пометив сверху его разряд единиц. Прикрыть этой полоской бумаги верхнее из наших чисел, совместив разряды единиц [чисел, оставшихся видимыми,] по вертикали. Обозрев эту пару цифр, записать цифру разряда единиц их произведения прямо под чертой и по вертикали с меткой, а цифру разряда десятков — ещё ниже и на одну позицию левее. Сместить полоску на одну позицию влево. Обозрев две пары цифр, которые выстроились по вертикали теперь, просуммировать их произведения, начиная с той пары, что стоит правее, и записать цифру разряда единиц результата прямо под чертой и по вертикали с меткой, а цифру разряда десятков ещё ниже и на одну позицию левее. Снова сместить полоску и действовать как ранее.
Конкретный пример прояснит дело. Пусть даны числа 574 и 3891. Запишем их, как здесь показано, проведём снизу черту и запишем число 574 на отдельной полоске бумаги, поставив метку поверх цифры 4.
Прикроем нашей полоской верхнее число, так чтобы метка оказалась прямо над разрядом единиц нижнего числа.
Обозрев располагающуюся вертикально пару цифр, говорим: «36» и вписываем цифру 6 под чертой и вертикально с меткой, а цифру 3 ещё ниже и на одну позицию левее.
Смещаем полоску бумаги на одну позицию влево.
Обозрев две располагающиеся вертикально пары цифр, говорим: «63 и 4 будет 67». Вписываем 7 и 6.
Смещаем полоску бумаги на одну позицию влево.
Обозрев три располагающиеся вертикально пары цифр, говорим: «45 и 7 будет 52, да 32 будет 84». Вписываем 4 и 8.
Смещаем полоску как ранее.
Обозрев три располагающиеся вертикально пары цифр, говорим: «5 и 56 будет 61, да 12 будет 73». Вписываем 3 и 7.
Смещаем полоску как ранее.
Обозрев две располагающиеся вертикально пары цифр, говорим: «40 и 21 будет 61». Вписываем 1 и 6.
Смещаем полоску как ранее.
Обозрев вертикальную пару цифр, говорим: «15». Вписываем 5 и 1.
Теперь удаляем полоску бумаги, проводим внизу черту и складываем вместе две полученные строки.
Читатель заметит, что действие при каждой позиции нашей полоски бумаги — вещь совершенно обособленная, осуществляемая сама по себе безотносительно к остальной части решения. Следовательно, при возникновении сомнения насчёт какой-либо отдельной цифры в ответе, те цифры, суммой которых она является, могут быть проверены сами по себе; например, если у нас есть подозрение, что цифра 9 неверна, мы можем проверить цифру 7, стоящую прямо над ней, помещая полоску бумаги в позицию восьмого этапа наших выкладок, а затем и цифру 1, стоящую над 7, поместив полоску в позицию десятого этапа.
Когда верхнее из двух данных чисел содержит не более четырёх или пяти цифр, действовать согласно вышеизложенному Правилу сравнительно легко, но при по-настоящему длинном верхнем числе окажется удобным проходить каждый ряд произведений дважды — первый раз суммируя их разряды единиц и занося разряд единиц результата в верхнюю строку решения, а затем суммируя их разряды десятков. Так, ход рассуждения для шестого этапа может быть следующим: «5 и 7 будет 12, да 2 будет 14». Заносим 4, 1 в уме. «5 и 3 будет 8». Вписываем 8 [2].
При действии по такому видоизменённому способу в голове рождается следующее Правило.
Собирая разряды единиц набора произведений пар цифр, помнить, что если один из членов пары равен 1, то разряд единиц равен другому [члену пары]; если один [из них] равен 5, то разряд единиц будет 5 либо 0 соответственно тому, чётным или нечётным будет другой; если один [из них] равен 9, разряд единиц равен 10 минус другой.
Собирая десятки, помнить, что если один из членов пары равен 1 или если сумма двух членов меньше 7, то разряд десятков отсутствует; если один [из членов пары] равен 5, то разряд десятков равен количеству двоек, содержащихся в другом; если один [из них] есть 9, то разряд десятков равен другому минус 1.
Во многих случаях такие задачи на умножение длинных чисел требуют суммирования только двух строк [под чертой]; когда же появляется набор произведений, чья сумма содержит три цифры, возникает нужда в третьей строке; когда сумма набора произведений содержит четыре цифры — то в четвёртой, но такое возникает только в том случае, когда меньшее из чисел содержит по меньшей мере тринадцать цифр; а когда сумма произведений содержит пять цифр — нужен пятый ряд, но такое происходит, лишь если меньшее число содержит по крайней мере сто двадцать четыре цифры, а потому превышает триллион секстиллионов!
Данный способ легко приложим и к перемножению десятичных дробей; нужно лишь для начала поместить полоску бумаги так, чтобы метка пришлась строго по вертикали над тем разрядом десятичных, на который требуется перенести действие. Я приведу здесь два примера, выделив из хода решения каждого, во-первых, сам пример в его исходной записи; во-вторых, стадию прямо перед тем, как полоска будет смещена первый раз; в-третьих, конечное состояние — перед тем как полоска будет убрана; и в-четвёртых, итог складывания.
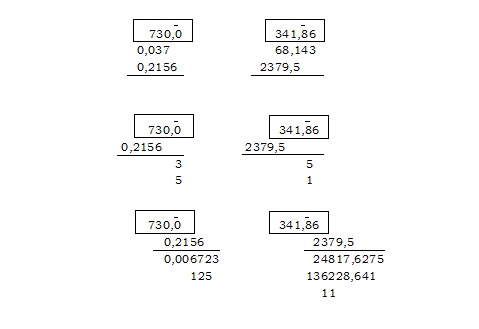
Следовательно, ответ в первом примере будет 0,0080 с точностью до четвёртого знака; во втором примере ответ, с точностью до второго знака, будет 16211446,27.
Глава 2. ДЕЛЕНИЕ ДЛИННЫХ ЧИСЕЛ, КОГДА ИСКОМЫМ ЯВЛЯЮТСЯ КАК ЧАСТНОЕ, ТАК И ОСТАТОК
§1. Делитель вида (10n ± 1) [3]
Год назад я обнаружил один любопытный [4] факт: если поставить «0» над разрядом единиц некоторого данного числа, которому случится быть кратным 9, и вычесть во всю длину, всякий раз ставя разность над следующей цифрой, то конечное вычитание даст 0 в остатке, а верхний ряд, по отбрасывании его конечного нуля, оказывается «частным-9» данного числа (то есть, частным от деления данного числа на 9).
Обнаружив этот факт, я тот час пришёл, по аналогии, к открытию того, что если поставить 0 под разрядом единиц некоторого данного числа, которому случится быть кратным 11, и действовать подобным образом, мы придём к подобному же результату.
В каждом случае я получал частное от деления столбиком более коротким и простым способом вычитания; но поскольку к этому результату можно было придти лишь в том (сравнительно редком) случае, когда данное число оказывалось точным кратным 9 или 11, это открытие виделось более любопытным, чем полезным.
Позднее я стал рассматривать случаи, когда данное число не было точным кратным. Я нашёл, что конечное вычитание при этом приносило некоторое число, иногда сразу являвшееся действительным остатком, получаемым от деления, но в любом случае дающее заготовку для нахождения такого остатка. Но поскольку оно не приносило частного (кроме как посредством некоторой весьма «экстравагантной» процедуры, значительно более длинной и трудоёмкой, чем подлинное деление), это открытие также не подлежало практическому применению.
Но совсем недавно мне пришло на ум выяснить, что будет, если после нахождения остатка поместить этот последний вместо того нуля над или под разрядом единиц, а затем вычесть как ранее. Меня поразило открытие того факта, что прежний результат повторился: конечное вычитание принесло 0 в остатке, а новая строка, по отбрасывании её разряда единиц, оказалась требуемым частным.
Существует, далее, более короткая процедура получения «остатка-9» и «остатка-11» некоторого данного числа, чем моё правило вычитания (процедура нахождения «остатка-11» есть ещё одно моё открытие). Усвоив её, я 28 сентября 1897 года довёл моё правило до завершения (я записал точную дату, поскольку это так приятно — быть открывателем новой и, как я надеюсь, практически полезной истины).
(1) Правило нахождения частного и остатка от деления данного числа на 9.
Чтобы найти «остаток-9», суммируем цифры; затем суммируем цифры результата и так далее, пока не останется единственная цифра. Если она будет меньше 9, это и будет искомый остаток; если это будет 9, искомый остаток равен нулю.
Чтобы найти «частное-9», проводим черту под нашим числом и ставим его «остаток-9» под разрядом единиц; затем вычитаем верхнее из нижнего, ставя разность под следующей цифрой, и так далее. Если крайняя левая цифра нашего числа меньше, чем 9, при её вычитании мы должны получить в остатке 0; если же она равна 9, мы должны получить в остатке 1, поставить в нижнюю строку да вычесть 1 заимствованное, что даёт в остатке 0. Теперь отчеркнём наш «остаток-9» на правом конце нижней строки, и оставшееся в ней будет «частным-9».
Примеры.
(2) Правило нахождения частного и остатка от деления данного числа на 11.
Чтобы найти «остаток-11», начинаем от разряда единиц и суммируем первую, третью и т. д. цифры, а также вторую, четвёртую и т. д.; находим «остаток-11» по разности этих сумм. Если первая сумма — большая, полученное таким образом число и будет искомым остатком; если же первая сумма — меньшая, искомый остаток будет разностью между полученным числом и числом «11»; если суммы равны, он есть 0.
Чтобы найти «частное-11», проводим черту под нашим числом и ставим его «остаток-11» под разрядом единиц; затем вычитаем <обычным порядком>, ставя разность под следующей цифрой, и так далее. Конечное вычитание должно дать в остатке 0. Теперь отчеркнём наш «остаток-11» на правом конце нижней строки, и оставшееся будет «частным-11».
Примеры.
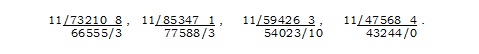
Эти новые Правила имеют ещё одно преимущество перед правилом подлинного деления, а именно что конечное вычитание обеспечивает нас критерием корректности результата: если оно не даёт в остатке 0, суммирование выполнено неверно, а если даёт, то либо суммирование выполнено верно, либо мы допустили две ошибки, — случай редкий.
Математикам не нужно и говорить, что правила, аналогичные вышеизложенным, с необходимостью будут действовать и для таких делителей, как 99, 101, 999, 1001 и т. д. Единственное видоизменение, которое необходимо будет внести — это разбить данное число на периоды по две или более цифр и обращаться с каждым таким периодом точно так же, как вышеизложенные правила требовали поступать с отдельными цифрами. Вот, для примера, целиком решение, требуемое для деления двух данных чисел на 999 и на 1001:
В первом из этих примеров число 2|437, написанное поверх, есть сумма по периодам. Поскольку она содержит 2 периода, поступаем с ней тем же образом, и итог, число 439, есть «остаток-999».
Во втором примере число 1|2269, написанное поверх, есть сумма первого и третьего периодов; число же 1383 есть сумма второго и четвёртого. Разность этих сумм равна 10886, чей «остаток-10001» равен 885 [5].
§2. Делитель вида (h10n ± k), в котором по крайней мере одно из двух чисел, h и k, больше 1 [6]
Способ, к которому мы приступаем теперь, приложим к трём отличным случаям:
(1) когда h > 1, k = 1;
(2) когда h = 1, k > 1;
(3) когда h > 1, k > 1.
При определённых ограничениях в отношении величин h, k и n, этот Способ окажется более короткой и более надёжной процедурой, чем обычное деление столбиком. Ограничения эти таковы: ни h, ни k не должны превышать 12, и когда k > 1, n не должно быть меньше, чем 3; вне этих ограничений нашему Способу присущи трудности, которые делают предпочтительной обычную процедуру.
При данном Способе требуются две раздельные процедуры — одна предназначена для случаев, когда h > 1, другая же для случаев, когда k > 1. Первая из этих процедур была, я полагаю, впервые открыта мной, а вторая — моим племянником, мистером Бертрамом Дж. Коллингвудом, который сообщил мне свой Способ, пригодный для делителей вида 10n – k.
В нижеследующем изложении я заменяю «10» буквой t [7].
Способ мистера Коллингвуда для делителей вида tn – k может быть изложен следующим образом:
«Чтобы разделить данное число на tn – k, отделяем в нём период из n цифр, начиная от разряда единиц, а затем записываем под ним увеличенное в k раз число, остающееся от первоначального при вычёркивании этого периода. Если это число содержит более чем n цифр, поступаем с ним тем же образом — и так далее, пока не будет достигнуто число, содержащее менее n цифр. Затем всё суммируем снизу доверху. Если последний период итога плюс увеличенная в k раз цифра, что была заимствована у него в процессе суммирования, будет меньше, чем наш делитель, то это и есть искомый остаток; оставшаяся часть итога есть искомое частное. Если этот [период] не меньше [делителя], то находим, какое количество раз он вмещает делитель, прибавляем это количество к частному и вычитаем это кратное делителя из остатка».
Например, чтобы разделить число 86781592485703152764092 на 9993 (то есть на t4 – 7), действуем так:
Этот новый Способ лучше всего прояснить, если начать со случая (3); легко будет видеть, какие изменения следует в нём произвести, когда дело перейдёт на случаи (1) и (2).
Правило для случая (3) и при знаке «–», может быть изложено так.
Разбить делимое, начиная с разряда единиц, на периоды по n цифр. При наличии с левой стороны избытка, меньшего, чем h, его не отграничивать, но отнести его и соседние n цифр к одному периоду.
Чтобы выстроить всю задачу, записываем делитель перед идущей за ним двойной вертикальной чертой, далее записываем делимое, разбитое на соответствующие периоды одинарными вертикальными чертами так, чтобы каждое пространство от черты до черты вмещало по n + 2 цифры. Под делимым проводим одинарную черту, а ещё ниже — двойную, оставив между ними пространство для внесения частного с расположением его разряда единиц под таковым предпоследнего периода делимого, а также остатка с расположением его разряда единиц под таковым последнего периода делимого. В этом пространстве и в пространстве ниже двойной черты проводим вертикальные черты, соответствующие таковым в делимом; а последнюю в верхнем пространстве делаем двойной, чтобы отделить частное от остатка.
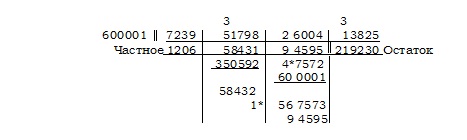
Например, если нам нужно разделить число 5984407103826 на 6997 (то есть на 7t3 – 3), то вся задача, подготовленная для решения, будет выглядеть так:
Чтобы решить этот пример, разделим первый период на h, внесём частное от этого деления в первый столбец под двойной линией и поместим остаток от него над вторым периодом, где он будет выполнять роль префикса к этому периоду. Ко второму периоду с его префиксом прибавим увеличенное в k раз число из первого столбца и внесём результат в верхнюю ячейку второго столбца [под двойной чертой]. Если это число не меньше, чем наш делитель, то найдём, какое количество раз оно вмещает делитель и внесём это количество в первый столбец и его же, увеличенное в k раз, во второй; затем проведём черту под вторым столбцом и приплюсуем это новое значение, вычитая из результата число, только что введённое в первую колонку, увеличенное в tn раз; а затем просуммируем первую колонку, вписывая результат в графу «Частное». Если число вверху второй колонки меньше, чем делитель, то число в первой колонке можно вносить в «Частное» сразу же. Число, внесённое в графу «Частное», и число в самом низу второй колонки суть наши частное и остаток, которые получились бы, если бы делимое оканчивалось своим вторым периодом. Теперь возьмём число, что в самом низу второй колонки, как новый второй период, и третий период как новый второй период и продолжим как ранее.
Верхний пример, решаемый в соответствие с этим Правилом, будет выглядеть так:
Ход рассуждения при этом следующий.
Делим число 5984 на 7, внося частное, 854, в первый столбец и помещая остаток, 6, над вторым периодом. Затем прибавляем к 6407 утроенное 854, внося результат во второй столбец следующим образом. «7 и 12 будет 19». Вносим 9, 1 в уме. «1 и 15 будет 16». Вносим 6, 1 в уме. «5 и 24 будет 29». Вносим 9, 2 в уме, которое, прибавленное к префиксу 6, даёт 8, которое также вносим. Отметив для себя, что это 8969 не меньше, чем наш делитель, и что оно содержит этот делитель единожды, вносим 1 в первый столбец, трижды 1 — во второй, затем проводим снизу черту и приплюсовываем это новое значение, не забывая вычесть из результата усемерённое t3, то есть 7000; в итоге получаем 1972. Затем суммируем первый столбец снизу вплоть до двойной черты и вносим результат, 855, в графу «Частное». Теперь берём 1972 как новый первый период, а третий период, 103, как новый второй период, и продолжаем как ранее следующим образом [8]. Проводим двойную черту под 1972 и делим его на 7, внося частное от деления, 281, под двойную черту, а остаток, 5, ставя над третьим периодом. Затем прибавляем к 5103 утроенное 281, внося результат, 5946, в третий столбец; отмечаем для себя, что он меньше делителя. Затем суммируем второй столбец снизу вплоть до ближайшей двойной черты и вносим результат, 281, в графу «Частное». Теперь берём 5946 как новый первый период, а конечный период, 826, как новый второй период, и продолжаем как ранее следующим образом. Проводим двойную черту по 5946 и делим его на 7, внося частное, 849, под двойную черту, а остаток, 3, ставя над конечным периодом. Теперь прибавляем к 3826 утроенное 849, внося результат, 6373, который, как можно было предвидеть, непременно будет меньше делителя, в ячейку «Остаток». Затем суммируем третий столбец снизу вплоть до ближайшей двойной черты и вносим результат, 849, конечным периодом в графу «Частное».
Было бы неплохо разъяснить действительную сущность трёх процедур, описанных в девятом предложении предыдущего абзаца, а именно 1) вносим 1 в первый столбец, 2) трижды 1 — во второй, 3) приплюсовываем это новое значение, не забывая вычесть 7000. Сущность 2) и 3), взятых в совокупности, заключается в увеличении второго столбца на 3 и в уменьшении его на 7000, то есть в уменьшении его на 7000 – 3, что равняется 6997. Сущность же 1) заключается в оправдании этого 6997, вычтенного, таким образом, из остатка (а последний тем самым оказался сведён к настоящему остатку), добавлением единицы к частному (которое, таким образом, превращается в настоящее частное).
Правило для случая (3) при знаке «+» может быть выведено из вышеизложенного правила простой заменой знака при k. Это, однако, вводит одно новое явление, которое должно быть предусмотрено следующей дополнительной оговоркой.
Когда вы прибавляете ко второму периоду, [взятому вместе] с его префиксом, число из первого столбца, увеличенное в (– k) раз, то есть когда вы вычитаете увеличенное в k раз это число из второго периода, [взятого вместе] с его префиксом, иногда может случиться так, что вычитаемое превосходит уменьшаемое. В этом случае вычитание будет оканчиваться цифрой-минус, которую можно пометить звёздочкой. Теперь ищем, какое количество наших делителей следует прибавить ко второму столбцу, чтобы погасить эту цифру-минус, и вносим это количество, помеченное звёздочкой, в первый столбец, а это кратное нашего делителя — во второй; затем проводим черту под вторым столбцом и приплюсовываем это новое значение.
В качестве примера возьмём новое делимое, но оставим прежний делитель, изменив знак при k, так что делителем станет число 7003 (то есть 7t3 + 3). Наша задача, подготовленная для решения, будет выглядеть так:
По окончании решения вид у неё будет такой:
Начало хода рассуждения таково.
Делим 6504 на 7 и вносим частное от деления, 929, в первый столбец, а остаток, 1, пишем поверх второго периода. Затем вычитаем из 1318 утроенное 929, внося результат во второй столбец следующим образом. «27 из 8 [вычесть] нельзя, но 27 из 28 будет 1». Вносим 1, занятое 2 в уме. «8 из 1 [вычесть] нельзя, но 8 из 11 будет 3». Вносим 3, занятое 1 в уме. «28 из 3 [вычесть] нельзя, но 28 из 33 будет пять». Вносим 5, занятое 3 в уме. «3 из 1 будет минус 2». Вносим его со звёздочкой. Отметив, что для погашения этого минус 2 достаточно будет прибавить делитель единожды, вносим (–1) в первый столбец, а 7003 — во второй; затем проводим черту под вторым столбцом и приплюсовываем это новое значение; в итоге получаем 5534. Затем суммируем первый столбец снизу доверху и вносим результат, 928, в графу «Частное». Теперь берём 5534 как новый первый период, а третий период, 972, как новый второй период, и продолжаем как ранее [9], следующим образом. Проводим двойную черту под 5534 и делим его на 7, внося частное от деления, 790, под двойную черту, а остаток, 4, ставя над третьим периодом. Затем вычитаем из 4972 утроенное 790, занося результат, 2602, в третий столбец; отмечаем для себя, что он не содержит цифр-минус. Затем суммируем второй столбец снизу вплоть до ближайшей двойной черты и вносим результат, 790, в графу «Частное». Теперь берём 2602 как новый первый период, а конечный период, 526, как новый второй период, и продолжаем как ранее следующим образом. Проводим двойную черту по 2692 и делим его на 7, внося частное, 371, под двойную черту, а остаток, 5, ставя над конечным периодом. Затем вычитаем из 2556 утроенное 371, занося результат, 4413, который, как можно было предвидеть, непременно будет меньше делителя, в ячейку «Остаток». Затем суммируем третий столбец снизу вплоть до ближайшей двойной черты и заносим результат, 371, конечным периодом в графу «Частное».
Правила для случая (1) могут быть выведены из вышеизложенного, принимая k = 1, а для случая (2) — принимая h = 1. Ниже я дам решённые примеры, а давать мысленные рассуждения здесь нужды нет.
Приняв k = 1, мы получаем делитель вида htn + 1; выберем делители 11t4 – 1 и 6t5 + 1.
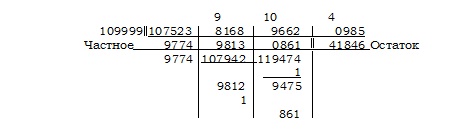
В этом последнем примере нет нужды вносить частное от деления 7239 на 7 в первый столбец; и так легко предвидеть, что число поверх второго столбца будет меньше нашего делителя, так что в первом столбце новых значений не появится; следовательно, мы сразу вносим 1206 в графу «Частное».
Принимая h = 1, получаем делители вида tn ± k; возьмём делители t4 – 7 и t5 + 12.
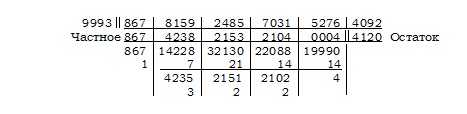
Первую из этих двух задач я привёл для того, чтобы проиллюстрировать открытый мистером Коллингвудом способ решения для делителей вида tn – k.
Читателю, возможно, интересно будет взглянуть на три способа решения вышеприведённого примера — обычное деление в столбик, способ мистера Коллингвуда и мою версию последнего — ради сравнения того количества усилий, которые каждый из них требует для своего решения:
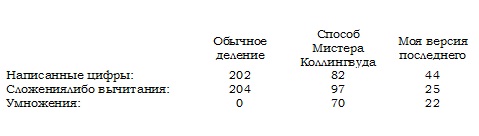
Я предполагаю, что всякий, кто станет решать это пример обычным делением, начнёт с создания таблицы кратных числа 9993 для справок, так что совершать умножения ему не придётся. Тем не менее, большое количество сложений и вычитаний, которые ему придётся совершать, влекущее гораздо больший риск ошибиться, чем каждый из двух других способов, вполне перевесит это преимущество.
Но какая бы из упомянутых процедур не привлекалась для деления длинных чисел, весьма желательно получить быстро и легко применимый способ проверки правильности ответа. В обычном случае для проверки перемножают частное с делителем, прибавляют остаток и смотрят, не будет ли всё вместе, как это и положено, образовывать исходное число.
Так, если N– это данное число, D–делитель, Q–частное, а R — остаток, то должно получиться:
N = DQ + R.
Этот способ проверки особенно легко применим, когда D = htn ± k, поскольку тогда должно быть:
N = (htn ± k)Q + R = (hQtn + R) ± kQ.
Теперь, hQtn можно найти умножением Q на h с присоединением n нулей. Следовательно, выражение hQtn + R находится подстановкой R на место этих n нулей. Если R содержит менее n цифр, недостающие вставляются перед ним нулями; если более, то избыточные следует перенести в следующий разряд и прибавить к hQ.
Вычислив наш «Критерий», то есть [значение выражения] hQtn + R, мы можем записать его на отдельной полоске бумаги и поместить ниже решения нашего примера, так чтобы он пришёлся прямо под N, которое будет располагаться сверху. Когда при D стоит знак «–», нам следует прибавить kQ к N и посмотреть, равен ли результат нашему «Критерию»; когда же знак «+», следует прибавить kQ к «Критерию» и посмотреть, равен ли результат N.
Уже указывалось, что когда, при новом Способе, решены первый и второй столбцы, то первый период частного и число внизу второго столбца суть частное и остаток, которые получились бы, если бы делимое оканчивалось своим вторым периодом. Следовательно, «Критерий» можно тут применить сразу, до переноса действия на третий столбец. Это составляет очень важную новую особенность моей версии способа мистера Коллингвуда. Каждые две соседствующие колонки содержат отдельную задачу на деление, которая может быть проверена сама по себе. Следовательно, как только, при решении моим способом, я внёс в графу «Частное» первый период, я могу её проверить и, в случае ошибки, исправить. Но тот злополучный вычислитель, который потратит, скажем, час времени, на деление некоего гигантского числа — обычным ли способом в столбик либо методом мистера Коллингвуда — и кому случится написать ошибочный результат на самом первом шагу, отчего и все последующие шаги оказываются неверны, — тот и не всполошится, пока не подойдёт к «горькому концу» и не начнёт проверять свой ответ. В то же время, следуя моей методике, он обратил бы внимание на ошибку почти тот час, как её сделал, и был бы в состоянии её исправить, пока не зашёл далеко.
В качестве пособия для читателя я целиком изложу ход рассуждения для второго и третьего столбцов первого из примеров, решённых выше.
Наш делитель есть число 6997 (где h = 7, k = 3). Здесь предполагается, что в графу «Частное» уже внесено 281. Делимое для этих двух столбцов есть 1972 | 103; частное 281, а остаток 5946. «Критерий» есть [выражение] hQtn + R (то есть 7 ? 281000 + 5946), и начало хода рассуждения таково. На отдельной полоске бумаги записываем последние три цифры R, а именно 946, и переносим 5 в следующий разряд, прибавляя её к 7 ? 281 следующим образом. «5 и 7 будет 12». Вносим 2, 1 в уме. «1 и 56 будет 57». Вносим 7, 5 в уме. «5 и 14 будет 19». Вносим. Вычислив «Критерий», проверяем, равняется ли ему [выражение] N + kQ. Вычисляем это последнее, сравнивая его по мере продвижения с нашим «Критерием» цифра за цифрой следующим образом. «3 и 3 будет 6». Сравниваем с «Критерием». «0 и 24 будет 24». Сравниваем 4, 2 в уме. «3 и 6 будет 9». Сравниваем. «1972 и 0 будет 1972». Сравниваем. «Критерий» удовлетворён.
Для делителей вида tn ± k нет нужды записывать «Критерий»: составляющие его числа уже находятся в решении и могут быть использованы на своих местах.
Глава 3. ДЕЛЕНИЕ ДЛИННЫХ ЧИСЕЛ, КОГДА ИСКОМЫМ ЯВЛЯЕТСЯ ОСТАТОК, НО НЕ ЧАСТНОЕ
§1. Делитель вида (tn ± 1)
Искомые способы были рассмотрены в §1 предыдущей главы как процедуры, предваряющие нахождение частного.
В случае делителей прочих обсуждаемых здесь видов способы, предназначенные для нахождения частного и остатка, пригодны, разумеется, и для нахождения одного лишь остатка; нам нужно будет рассмотреть здесь только те случаи, когда, коль скоро частное нам не требуется, эти способы поддаются сокращению.
§2. Делитель вида (ht ± 1)
А именно: те способы, что были рассмотрены в §1 предыдущей главы, могут быть здесь сокращены удалением всего письменного решения под двойной чертой.
Для примера такого сокращённого способа возьмём число 27910385642558361 в качестве делимого и найдём его «остаток-29» и «остаток-71».
В первом случае по решении установится вид:
ход же рассуждения будет таков. Начинаем с деления 27 на 3 и прибавления частного, 9, к числу, образованному добавлением в качестве префикса остатка, 0, к следующей цифре, 9; то есть говорим: «9 и 9 будет 18». Затем делим это 18 на 3 и прибавляем частное, 6, к числу, образованному добавлением в качестве префикса остатка, 0, к следующей цифре, 1; то есть говорим: «6 и 1 будет 7». Затем говорим: «2 и 10 будет 12, 4 и 3 будет 7, 2 и 18 будет 20, 6 и 25 будет 31». Тут мы «отбрасываем» 29 и говорим: «что даёт 2». Объединяем её со следующей цифрой, 6, продолжая так: «8 и 24 будет 32, что даёт 3; 1 и 2 будет 3, 1 и 5 будет 6, 2 и 5 будет 7, 2 и 18 будет 20, 6 и 23 будет 29, что даёт 0; 2 и 1 будет 3, 1 и 2 будет 2».
Во втором случае по решении установится вид:
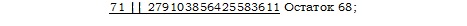
ход же рассуждения будет таков. Начинаем с деления 27 на 7 и вычитания частного, 3, из числа, образованного добавлением в качестве префикса остатка, 6, к следующей цифре, 9; то есть говорим: «3 из 69 будет 66». Затем делим это 66 на 7 и вычитаем частное, 9, из числа, образованного добавлением в качестве префикса остатка, 3, к следующей цифре, 1; то есть говорим: «9 из 31 будет 22». Затем говорим: «3 из 10 будет 7, 1 из 3 будет 2, 0 из 28 будет 28, 4 из 5 будет 1, 0 из 16 будет 16, 2 из 24 будет 22, 3 из 15 будет 12, 1 из 55 будет 54, 7 из 58 будет 51, 7 из 23 будет 16, 2 из 26 будет 24, 3 из 31 будет 28, 4 из 1 [вычесть] нельзя, но (тут мы вбрасываем добавочный делитель) 4 из 72 будет 68».
§3. Степени 10
«Остаток-10» есть последняя цифра, «остаток-102» есть число, образованное двумя последними цифрами и так далее.
Эти остатки годятся в качестве начальных делимых для всех чисел, множители которых есть степени множителей 10, тот есть [степени чисел] 2 и 5. Так, «остаток-32» можно найти, взяв число, образованное последними пятью цифрами и разделив его на 32. Точно так же 80 есть 24 ? 5; следовательно, «остаток-104» годится для того[, чтобы найти «остаток-80»].
§4. Множители делителей вида ht ± 1
«Остаток-21» годится в качестве начального делимого для 7 (множитель [числа 21] есть также множитель 9). Но этот остаток (из-за малой величины h, которая постоянно даёт вычитаемое, превосходящее уменьшаемое) находится с таким трудом, что лично я предпочитаю находить «остаток-7» обычным делением.
«Остаток-39» годится для 13, [остаток-] 51 — для 17, [остаток-] 69 — для 23.
. . . . . . . . . . .
. . . . . . . . . . .
. . . . . . . . . . .