Другіе способы дѣленія.

Другіе способы д?ленія.

1) Самымъ простымъ, общедоступнымъ путемъ д?ленія, правда длиннымъ и утомительнымъ, является зам?на д?ленія вычитаніемъ; поэтому вс? народы, которые находятся на низшихъ ступеняхъ развитія, производятъ д?леніе при ломощи вычитанія: потому также полезно было бы давать и малымъ д?тямъ н?сколько упражненій на посл?довательное вычитаніе, прежде ч?мъ переходить съ ними къ д?ленію. Прим?ровъ зам?ны д?ленія вычитаніемъ можно указать много у разныхъ народовъ, особенно же среди мало образованныхъ классовъ. Такъ, въ средніе в?ка въ Германіи среди простого народа часто употреблялся счетъ на маркахъ, т.-е. на костяшкахъ—костяшки эти клались въ колонны, въ особую колонну для каждаго разряда— въ такомъ случа? д?литель откладывался отъ д?лимаго столько разъ, сколько было возможно, и число отложенныхъ д?лителей показывало величину отв?та, потому что разд?лить—значитъ узнать, сколько разъ д?литель содержится въ д?лимомъ.

2) Зам?на д?ленія умноженіемъ н?сколько трудн?е, ч?мъ зам?на его вычитаніемъ; она не такъ доступна, понятна и наглядна; ее мы встр?чаемъ на т?хъ ступеняхъ развитія науки, когда совершается переходъ отъ простонародныхъ пріемовъ вычисленія къ точнымъ научнымъ пріемамъ. Такъ, напр., у индусовъ до выработки нормальныхъ способовъ д?ленія мы видимъ массу попытокъ привести его къ умноженію; при этомъ и само умноженіе совершается такимъ искусственнымъ порядкомъ, какой встр?чается еще въ глубокой древности у египтянъ, распространенъ былъ среди вс?хъ народовъ и пользуется до сегодня популярностью среди самоучекъ и немудрыхъ счетчиковъ. Для поясненія беремъ прим?ръ у Евтокія, греческаго писателя въ VI в. по Р. X. Требуется разд?лить 6152 на 15. Для этого Евтокій составляетъ рядъ чиселъ, кратныхъ 15-ти: 15, 30, 60, 90, 120,150, 180, 210: 240, 270, 300, 600, 900,1200, 1800, 2100, 2400, 2700, 3000, 6000. Рядъ этотъ, какъ видимъ, содержитъ не вс? кратныя числа, но онъ только пролагаетъ путь къ тому, чтобы догадаться, что 6000 кратно 15, и что въ 6000 содержится 15 четыреста разъ. Остается теперь разд?лить 152 на 15. Для этого Евтокій снова соcтавляетъ подобный же рядъ: 15, 30, 60, 90, 150 и выводитъ, что 15 въ 150-ти содержится 10 разъ. Всего въ отв?т? получится 410 и 2 въ. остатк?.

3) Сл?дующей попыткой къ упрощенію д?ленія является расчлененіе д?лителя на производителей; оно и теперь прим?няется съ большимъ усп?хомъ, особенно при устномъ счет?; именно, чтобы разд?лить, напр., на 8, можно разд?лить данное число пополамъ, полученный отв?тъ опять пополамъ и вновь полученный отв?тъ еще разъ пополамъ. Для письменнаго вычисленія такой порядокъ особенно рекомендуется итальянцемъ Леонардо Фибонначи (около 1200 г. по Р. X.); при этомъ, въ случа? дробнаго частнаго, у него получаетея рядъ дробей съ возрастающиии знаменателями.

Оригинальный пріемъ, основанный на той же иде?, даетъ Апіанъ (XVI в. по Р. X.); у него проскальзываетъ н?что въ род? десятичныхъ дробей, хотя въ его время теорія десятичныхъ дробей находилась въ самомъ зачаточномъ состояніи.

Положимъ, ему надо разд?лить 11664 на 48; онъ сперва вычисляетъ 11664:6, потомъ отъ каждаго полученнаго разряда беретъ вооьмую долю, это легко достигается т?мъ, что каждый разрядъ по-множается на 0125, такъ какъ 1:8=0,125. Все д?йствіе можно представить въ такомъ вид?.

Объясняется это вычисленіе сл?дующимъ образомъ. Д?лимъ 11 тыс. на 6, получаемъ 5 въ остатк? и 1 въ частномъ; 5 пишемъ надъ 1, а единицу частнаго умножаемъ на 0125 и пишемъ прямо подъ чертой. Дал?е, 56 сот.: 6=9 сот. и 2 сотни въ остатк?; остатокъ пом?щаемъ надъ 6-ю, а 9 надо умножить на 0125; для этого Апіанъ множитъ отд?льно 0125 на 5 и на 4, получаетъ 0625 и 05; при записываніи цифра 5 у числа 0625 подвигается вправо за черту, потому что это будутъ уже не ц?лыя единицы, а только десятыг доли. Теперь 26 десятковъ надо д?лить на 6, будетъ въ частномъ 4 десятка; помножить 4 на 0125, получится 5—столько простых единицъ, ихъ пишемъ. Наконецъ, 24:6 — 4, 4?0125 = 5, это будутъ десятыя доли, и ихъ сл?дуетъ писать за чертой вправо. Остается сложить вс? отд?льныя частныя и тогда получится общій отв?тъ 243.

4) Вс? три предыдущихъ способа уступаютъ нашему, которымъ мы, обыкновенно, пользуемся: они трудн?е и длинн?е нашего. Но вотъ методъ Тиллиха, предложенный имъ въ 1806 г. Онъ уже вытекаетъ изъ нормальнаго пріема и стремится еще бол?е его усовершенство-вать. Суть его состоитъ въ сл?дующемъ. При д?леніи на однозначное число, напр., на 3, не сносятъ остатковъ къ сл?дующему низшему разряду, а стараются разд?лить каждый разрядъ вполн?, хотя бы для этого пришлось воспользоваться и дробнымъ частнымъ. Согласно этому, д?йствіе 56789:3 располагается такъ:

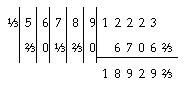
Прежде всего д?лится 5 дес. тысячъ на 3, на каждую часть придется по 1? дес. тысячъ, изъ этого 1 дес. тыс. сносится въ частное, а ? дес. тыс. пока оставляются. Зат?мъ д?лимъ 6 тысячъ на 3, будетъ по 2 тысячи, ихъ такъ и пишемъ въ частномъ. Точно такимъ же образомъ 7 сот.: 3 = 2? сотни, 8 дес.: 3 — 2? дес и наконецъ 9:3 = 3. При этомъ вс? ц?лые отв?ты сносятся въ частное, а дроби пока оставляются. Дроби эти приводятся къ нормальному виду сл?дующимъ путемъ. ? десятка тысячъ дадутъ 6 тысячъ и ?тысячи; эти ? тысячи составятъ 6? сотни, да у насъ еще ? сотни, всего получится 7 сотенъ, ихъ такъ и пишемъ. Останется только церевести ?десятка въ единицы, будетъ 6?. Окончательный отв?тъ составитъ 18929?.

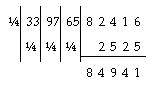
Въ иныхъ прим?рахъ можно разбивать д?лимое на группы въ 2 разряда, и это представляетъ немалое удобство. Такъ, ? отъ 339765 Тиллихъ сов?туетъ находить д?леніемъ 33 дес. тысячъ на 4, 97 сотенъ на 4 и 65-ти единицъ на 4. Тогда форма вычисленія получится сл?дующая: