Австрійскій способъ дѣленія.
Австрійскій способъ д?ленія.
Подъ именемъ австрійскаго способа разум?ется такой, который хотя и похожъ на нашъ нормальный, но отличается отъ него большімъ прим?неніемъ устнаго счета. Австрійскій способъ можно считать шагомъ впередъ сравнительно съ нашимъ способом, въ немъ меньше шісьма и самое д?йствіе совершается всл?дствіе этого гораздо быстр?е, правда, есть въ немъ и неудобство: именно, челов?къ, мало-мальски невнимательный, легко въ немъ сд?лаетъ ошибку и собьется. Для прим?ра возьмемъ 167585 : 365. Первая цифра частнаго будетъ 4; составляемъ произведеніе 365 на 4, начиная съ низшихъ разрядовъ, но не подписываемъ этого произведенія подъ д?лимымъ, а вычитаемъ каждый разрядъ его, какъ только онъ получится, и пишемъ прямо остатокъ: 4?5=20, сл?д. въ остатк? 5; 4?6=24, да 2, 26, 6 изъ 7=1, сл?д. въ остатк? 1; дал?е 3?4=12 да 2—14, 14 изъ 16 даетъ въ остатк? 2; всего получится посл? вычитанія 215; сносимъ сл?дующую цифру 3 и д?лимъ новое число 2153 такъ же, какъ и предыдущее, т.-е. одновременно производимъ умноженіе и вычитаніе.
Австрійская метода стала выдвигаться на первый планъ сравнительно недавно, съ средины XIX в?ка, но зачатки ея простираются вплоть до XVII в?ка; еще Вендлеръ даетъ образецъ такого сокращеннаго д?ленія.

Кегель въ XVII ст. даетъ бол?е грубую форму этого способа, такъ какъ онъ начинаетъ умноженіе съ высшихъ разрядовъ, а не съ низшихъ и ему приходится лишній разъ изм?нять цифры. Вотъ какъ у него идетъ д?леніе 135513 на 21:
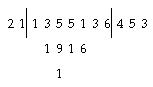
Наконецъ, Маурахеръ (XVIII в.) пользуется такимъ расположеніемъ вычисленія:

При этомъ частное 12345 пом?щается внизу, д?литель 8 сл?ва, а д?лимое 98760 прав?е д?лителя.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
Австрійскій способъ дѣленія.
Австрійскій способъ д?ленія. Подъ именемъ австрійскаго способа разум?ется такой, который хотя и похожъ на нашъ нормальный, но отличается отъ него большімъ прим?неніемъ устнаго счета. Австрійскій способъ можно считать шагомъ впередъ сравнительно съ нашимъ способом, въ
Испанскій способъ дѣленія.
Испанскій способъ д?ленія. Это самая употребительная, самая распространенная форма д?ленія. Теперь ея уже н?тъ въ учебникахъ и объ ней не вспоминаютъ, но почти въ теченіе тысячи л?тъ, съ IX в?ка до XIX, она являлась общеизв?стной и популярной формой. Начало ей положили арабы;
Римскій способъ дѣленія.
Римскій способъ д?ленія. Римляне были расположены къ счету круглыми числами, и поэтому они любили зам?нять числа, близкія къ круглымъ, при посредств? этихъ круглыхъ. Прим?ровъ этому можно привести очень много, хотя бы: 18 по ихъ нумераціи выражается черезъ 20 безъ двухъ, 90
Другіе способы дѣленія.
Другіе способы д?ленія. 1) Самымъ простымъ, общедоступнымъ путемъ д?ленія, правда длиннымъ и утомительнымъ, является зам?на д?ленія вычитаніемъ; поэтому вс? народы, которые находятся на низшихъ ступеняхъ развитія, производятъ д?леніе при ломощи вычитанія: потому также
Правило пропорціональнаго дѣленія.
Правило пропорціональнаго д?ленія. Пропорціональное д?леніе съ давнихъ временъ прилагалось тогда, когда требовалось разд?лить зав?щанный капиталъ между насл?дниками. Поэтому въ сборникахъ, обыкновенно, пом?щалось н?сколько задачъ этого рода. Вотъ задача изъ сборника