Правило пропорціональнаго дѣленія.
Правило пропорціональнаго д?ленія.
Пропорціональное д?леніе съ давнихъ временъ прилагалось тогда, когда требовалось разд?лить зав?щанный капиталъ между насл?дниками. Поэтому въ сборникахъ, обыкновенно, пом?щалось н?сколько задачъ этого рода. Вотъ задача изъ сборника Магницкаго: «Н?кій челов?къ имяше жену и три сына и дщерь едину; той челов?къ при смерти своей написа въ зав?т? своемъ посл?ди себе разд?лити пожитки, жен? осмую часть всего им?нія, сыномъ же всякому ихъ вдвое при дщери своей, изъ т?хъ 7/8 всего им?нія, по смерти же его обр?теся им?нія на 48000 рублевъ, и в?дательно есть, колико кому досталось изъ того его всего им?нія; придетъ: жен? 6000 рублевъ, д?тямъ мужеску полу 12000 рублевъ, а дщери 6000 рублевъ:
Въ прежнее время авторы учебниковъ давали очень замысловатые вопросы касательно зав?щаній. Напр., они разсчитывали доли такъ, что сумма ихъ не составляла единицы, и тутъ приходилось много мудрить, прежде ч?мъ придти къ сносному р?шенію. Д?йствительно, если осталось три насл?дника, и первому отказано ? им?нія, второму ? и посл?днему ?, то какъ же тутъ поступить, в?дь эти доли образуютъ вм?ст? больше, ч?мъ ц?лое насл?дство, именно 13/12 насл?дства; въ такихъ случаяхъ брали, обыкновенно, отношеніе частей и по нимъ д?лили; въ нашемъ прим?р? ? : ? : ? = 6 : 4 : 3, сл?довательно, старшему сыну надо дать 6/13, второму 4/13 и третьему 3/13 всего насл?дства.
Любопытную задачу въ этомъ род? далъ знаменитый римскій юристъ Сальвіанъ Юліанъ, жившій при императорахъ Адріан? и Антонин? Пі? (во II в. по Р. X.)
«Н?кто, умирая, оставилъ беременную жену и зав?щалъ: если у меня родится сынъ, то пусть ему дано будетъ ? им?нія, а жен? остальная ?, если же родится дочь, то ей ? а жен? остальныя ?, родилась двойня, — сынъ и дочь, какъ же теперь разд?лить им?ніе?»
Сальвіанъ предложилъ сыну дать 4 части, жен? 2 и дочери 1. Задача считалась очень интересной и даже вошла въ пандекты, византійскій сборникъ законовъ. Между прочимъ, Алькуинъ, придворный математикъ Карла Великаго (въ VIII в. по Р. X.), думалъ надъ этой же задачей, но она изложена у него съ другими числами. По Алькуину, сыну зав?щано ? и вдов? ?, дочери 7/12 и вдов? 5/12. Къ задач? приложено переписчикомъ р?шеніе, съ которымъ согласиться нелегко: чтобы удовлетворить сына и мать, надо 12 долей, а еще дочь и мать 24 доли; по 1-му условію сынъ получаетъ 9 долей, мать 3, по второму — мать 5 и дочь 7, всего приходится матери
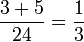
сыну —
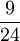
= ?, дочери

Вс? задачи на зав?щанія р?шались тройнымъ правиломъ и относились къ той групп?, которая въ старинныхъ русскихъ ари?метикахъ озаглавливалась: «статья д?ловая въ тройномъ правил?», т.-е. статья, гд? производитея д?лежъ, то былъ д?лежъ заработка, награды и т. п. За ней шла «торговая м?новая въ тройномъ правил?», т.-е. статья объ обм?н?, которая также приводилась къ тройному правилу. Потомъ «статья торговая складная и д?лительная», гд? прибыль д?лилась соотв?тственно вложенному капиталу. Зат?мъ «статья торговая складная съ прикащики и съ людьми ихъ», въ ней нужно было выд?лить кром? прибыли еще жалованіе прикащикамъ. И, наконецъ, шла «торговая складная со времены»: зд?сь принимался во вниманіе не только капиталъ, вложенный каждымъ компаньономъ въ предпріятіе, но и время оборота.
Задачи на пропорціональное д?леніе р?шались, обыкновенно, тройнымъ правиломъ, при этомъ не оставалось м?ста ни сокращеніямъ, ни упрощеніямъ и не давалось простора личной сообразительности ученика. Обыкновенно, сперва пом?щалось условіе вопроса, потомъ тутъ же р?шеніе, ученикъ все это заучивалъ и впосл?дствіи старался это прилагать, когда встр?чалъ вопросъ, похожій на заученный.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
Австрійскій способъ дѣленія.
Австрійскій способъ д?ленія. Подъ именемъ австрійскаго способа разум?ется такой, который хотя и похожъ на нашъ нормальный, но отличается отъ него большімъ прим?неніемъ устнаго счета. Австрійскій способъ можно считать шагомъ впередъ сравнительно съ нашимъ способом, въ
Испанскій способъ дѣленія.
Испанскій способъ д?ленія. Это самая употребительная, самая распространенная форма д?ленія. Теперь ея уже н?тъ въ учебникахъ и объ ней не вспоминаютъ, но почти въ теченіе тысячи л?тъ, съ IX в?ка до XIX, она являлась общеизв?стной и популярной формой. Начало ей положили арабы;
Римскій способъ дѣленія.
Римскій способъ д?ленія. Римляне были расположены къ счету круглыми числами, и поэтому они любили зам?нять числа, близкія къ круглымъ, при посредств? этихъ круглыхъ. Прим?ровъ этому можно привести очень много, хотя бы: 18 по ихъ нумераціи выражается черезъ 20 безъ двухъ, 90
Другіе способы дѣленія.
Другіе способы д?ленія. 1) Самымъ простымъ, общедоступнымъ путемъ д?ленія, правда длиннымъ и утомительнымъ, является зам?на д?ленія вычитаніемъ; поэтому вс? народы, которые находятся на низшихъ ступеняхъ развитія, производятъ д?леніе при ломощи вычитанія: потому также
Тройное правило.
Тройное правило. Н?тъ такого достаточно сильнаго выраженія, на которое поскупились бы составителя среднев?ковыхъ ари?метикъ, чтобы похвалить тройное правило. «Та строка тройная похвальная и лучшая строка изо вс?хъ иныхъ строкъ.» «Ее философы зовутъ золотою строкою». Въ
Правило процентовъ.
Правило процентовъ. Взиманіе процентовъ практиковалось еще въ древнія времена, но въ различныхъ государствахъ къ нему относились различно и вообще это д?ло было совершенно не урегулировано.У римлянъ допускались только простые проценты, онн высчитывались по одному въ
Цѣпное правило.
Ц?пное правило. Начало ц?пного правила можно просл?дить у индусовъ, именно, оно содержится въ ари?метик? индуса Брамегуиты, относящейся къ VII ст. по Р. X. Въ Германіи оно встр?чается раньше вс?хъ у Адама Ризе (въ XVI ст.); распространенію его особенно способствовалъ голландецъ
Фальшивое правило.
Фальшивое правило. Существовало и такое правило, и не только существовало, но пользовалось громаднымъ вниманіемъ. По крайней м?р?, у Магницкаго особая 4-я часть его ари?метики была посвящена правиламъ „фальшивымъ или гадательнымъ“, въ то время, какъ въ 1-й части шли