Римскій способъ дѣленія.

Римскій способъ д?ленія.

 Римляне были расположены къ счету круглыми числами, и поэтому они любили зам?нять числа, близкія къ круглымъ, при посредств? этихъ круглыхъ. Прим?ровъ этому можно привести очень много, хотя бы: 18 по ихъ нумераціи выражается черезъ 20 безъ двухъ, 90 черезъ сто безъ десяти и т. д. Естественно поэтому ожидать, что подобная наклонность къ круглымъ числамъ будетъ проявлена и при д?леніи. Прим?ръ 668 : 6 р?шается по римскому способу сл?дующимъ образомъ. Д?лимъ 668 не на 6 равныхъ частей, а на 10, тогда въ каждой части будетъ по 6 десятковъ, но в?дь мы взяли 4 лишнихъ части, и въ каждой по 6 десятковъ, всего, сл?д., взяли лишняго 24 десятка, эту сдачу надо приложить опять къ делимому, будетъ 308. Д?лимъ теперь 30 десятковъ на 10, будетъ въ каждой части по 3 десятка, и такъ какъ лишнихъ частей взято опять 4, то он? составятъ 12 дес, а поэтому всего осталось под?лить число 128. Изъ этого 12 дес. при д?леніи на 10 дадутъ въ каждой части по 1 дес. и сдачи образуется 4 дес. Всего мы, сл?д., набрали въ частномъ 6 д.+3 д.+1 д.=10 дес, или 100. Теперь надо 68 д?лить на 6. Продолжаемъ это д?лать т?мъ же самымъ пріемомъ, какимъ вели и до сихъ поръ, именно: 60 : 10, будетъ по 6 ед., сдачи 4?6=24, да 8, всего 32; д?лимъ 32 на 10, будетъ по 3, сдачи 3?4=12, да 2, всего 14; д?лимъ 14 на 10, будетъ по 1 единиц?, сдачи 4, да 4, всего 8, теперь число уже не д?лится на 10 и поэтому остается только вопомнить настоящаго д?лителя 6; и разд?лить на него, будетъ въ частномъ 1 и въ остатк? 2. Подсчитаемъ итогъ, сколько мы набрали всего-навсего единицъ: 6+3+1+1=11, и въ остатк? 2; десятковъ мы выше насчитали 10, и сл?д. окончательный отв?тъ представится въ вид? 100+11, т.-е. 111 и ост. 2. Вотъ какой длинный и кропотливый путь. Онъ составляетъ характерную принадлежность римской ари?метики, особенно же временъ упадка Рима и перехода римской цивилизаціи къ народамъ Западной Европы. Особенно подробно разработанъ этотъ способъ у Боэція (470—525 по Р. X.), знатнаго и ученаго римскаго гражданина, и у Герберта (папы Сильвестра II), жившаго около 1000 года по Р. X. Посл? Герберта этотъ способъ сталъ все бол?е и бол?е выт?сняться арабскими пріемами, т.-е. такими, которые близки къ нашему нормальному д?ленію. Не даромъ съ этихъ поръ стали называть способъ Боэція «жел?знымъ правиломъ», въ отличіе отъ «золотого» подъ которымъ чаше всего разум?ли «д?леніе вверху» .

Труденъ и очень труденъ былъ римскій способъ, значительно трудн?е, ч?мъ «д?леніе внизу» и «д?леніе вверху».

Обременительность его завис?ла прежде всего отъ его сложности, но кром? того, еще и отъ того, что педагоги и составители учебниковъ или не ум?ли, или не хот?ли объяснить д?ло, какъ сл?дуетъ. Высокимъ, ученымъ слогомъ, безъ обращенія къ чему-нибудь наглядному и понятному, они вели бес?ду такъ, какъ будто передъ ними находились тоже ученые люди или педагоги, а не малыя д?ти: тогдашняя школа м?ряла все на аршинъ учителя и не прим?нялась къ возрасту и развитію ученика.

Вотъ выписка изъ книжки Сперанскаго (Очерки по исторіи народной школы въ Западной Европ?, стр. 118, заимств. изъ Гюнтера): При д?леніи 5069 на 4, д?йствія располагаются сл?дующимъ образомъ. Мы им?емъ: 10—4=6,

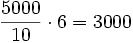
Образуемъ теперь произведеніе

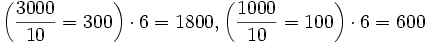
откуда мы получаем 600 + 800 = 1400. Точно также:

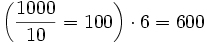
600+400=1000. Пользуясь все т?мъ же пріемомъ, вычисляемъ произведеніе

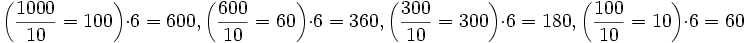
и образуемъ сумму 60+80+60+60=260. Дал?е:

а 60+20+60=140. Двигаясь т?мъ же путемъ дал?е, мы получимъ:

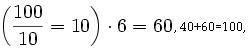
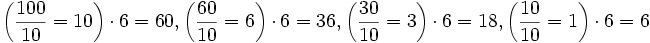
6+8+6+9=29. Зат?мъ находимъ

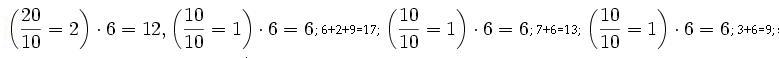
 эта сумма, подобно д?литеkю, является уже числомъ меньшимъ 10-ти. Такимъ образомъ оказывается, что остатокъ отъ д?ленія равенъ 1. Искомое частное 1267. Первоначально римскій способъ прим?нялся на абак?, при помощи римскихъ цифръ; но съ теченіемъ времени, когда въ Европу проникли арабскія цифры, онъ сталъ прим?няться и на нихъ и долго не уступалъ своего м?ста новымъ пріемамъ. Теперь онъ уже совершенно оставленъ и р?шительно нигд? не встр?чается. А между т?мъ и у него есть н?которое удобство, которое возвышаетъ его въ этомъ отношеніи: именно легкое угадываніе цифръ частнаго. Въ нашемъ нормальномъ д?леніи иногда случается задаваться не тою цифрою, какая нужна, а большей или менmiей; у римлянъ же это могло случаться гораздо р?же, потому что д?лителемъ у нихъ всегда служило круглое число, про которое легко найти, сколько разъ оно содержится въ д?лимомъ.

Приведемъ образцы письменнаго расположенія по этому способу. Прим?ры: 672 : 16 и 3276 : 84.