30. Шесть копеек

Надо разложить шесть копеечных монет в три прямых ряда так, чтобы в каждом ряду было по три копейки.

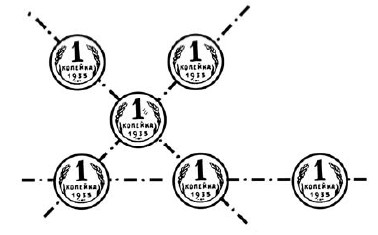
Вы думаете — это невозможно? Не хватает еще трех монет? А вот поглядите, они здесь расположены на рисунке.

Вы видите здесь три ряда монет, по три в каждом ряду. Значит, задача решена. Правда, ряды перекрещиваются, но ведь не запрещено было их перекрещивать.

Теперь попробуйте сами догадаться, как можно решить ту же задачу еще и другим способом.

Более 800 000 книг и аудиокниг! 📚

Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением

ПОЛУЧИТЬ ПОДАРОК

Данный текст является ознакомительным фрагментом.

Читайте также

Где были расположены шесть первичных Английских государств? Ответ фактически дан в предыдущем разделе. Это — государства (и народы) средневековой Европы XIII–XV веков, участвовавшие в покорении Византии и в великом = «монгольском» завоевании.1) Британия старых английских

94. Еще шесть силуэтов Попробуйте сложить из танграмов, нарисованных на рис. 92, геометрические силуэты: девушки, сидящей на траве (1), женщины, смотрящей в зеркало (2), головы в шляпе (3), Наполеона (4) и два силуэта краснокожих индейцев (5) и

116. Шесть четырехугольников В фигуре, представленной на рис. 112, нужно так переложить 6 спичек с одного места на другое, чтобы образовалась фигура, составленная из 6 одинаковых

149. Цифра шесть Спросите кого-нибудь из ваших знакомых постарше, как давно он обладает карманными часами. Положим, окажется, что часы у него уже 15 лет. Продолжайте тогда разговор примерно в таком духе:— А сколько раз в день вы обычно смотрите на свои часы?— Раз двадцать,

6. Шесть четырехугольников В фигуре, представленной на рис. 3, нужно так переложить 6 спичек с одного места на другое, чтобы образовалась фигура, составленная из 6 одинаковых

9. Цифра шесть Спросите кого-нибудь из ваших знакомых постарше, как давно он обладает карманными часами. Положим, окажется, что часы у него уже 15 лет. Продолжайте тогда разговор примерно в таком духе:– А сколько раз в день вы обычно смотрите на свои часы?– Раз двадцать,

30. Шесть копеек Надо разложить шесть копеечных монет в три прямых ряда так, чтобы в каждом ряду было по три копейки. Вы думаете — это невозможно? Не хватает еще трех монет? А вот поглядите, они здесь расположены на рисунке.Вы видите здесь три ряда монет, по три в каждом ряду.

34. Тридцать шесть нулей В клетках этой решетки расставлено, как видите, 36 нулей. Двенадцать из них надо зачеркнуть, но так, чтобы после этого в каждом вертикальном и горизонтальном ряду оставалось по одинаковому количеству незачеркнутых нулей.Какие же нули надо

34. Тридцать шесть нулей Так как из 36 нулей надо зачеркнуть 12, то должно остаться 36–12, т. е. 24, по 4 нуля в каждом ряду. Расположение незачеркнутых нулей таково (см.