7. Матрицы и действия над ними

Матрицей размерности m x n называется прямоугольная таблица вида:

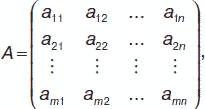
или А = (a_ij), где i = 1, 2…, m; j = 1, 2…, n. Числа a_ij – называются элементами матрицы. Если m = 1, а n > 1, то матрица является матрицей–строкой. Если m > 1, а n = 1, то матрица является матрицей–столбцом. Если m = n, то матрица называется квадратной, а число ее строк (или столбцов) называется порядком матрицы.

Две матрицы А и В называются равными, если их размер одинаков и a_ij = b_ij. Нулевая матрица – это матрица, у которой все элементы равны нулю.

Единичной матрицей называется квадратная матрица:

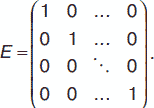
Матрицей, транспонированной к матрице А размерности m х n называется матрица А^т размерности n х m, полученная из матрицы А если ее строки записать в столбцы а столбцы – строки.

Матрицы одинакового размера (однотипные) можно складывать, вычитать, перемножать и умножать на число.

Суммой (разностью) двух однотипных матриц А и В называется матрица С, элементы которой равны сумме или разности c_ij = a_ij ± b_ij. При сложении справедливы:

А + В = В + А, (А + В) + С = А + (В + С), А + 0 = А.

Произведением матрицы А на число р называется матрица, элементы которой равны рa_ij.

Справедливы свойства:

?(?A) = (??)А;

(А + В)? = ?А + ?В;

(? + ?)А = ?А + ?А.

Произведением двух квадратных матриц А и В называется матрица С, элемент которой, находящийся на пересечении i–ой строки и k–го столбца, является суммой парных произведений элементов i–ой строки первой матрицы на элемент k–ой строки второй матрицы С = АВ. То же правило распространяется на умножение прямоугольных матриц, у которых число столбцов матрицы–множимого равно числу строк матрицы–множителя.

Матрицы, для которых АВ = ВА, называются коммутирующими.

Справедливы свойства:

1) ЕА = АЕ = А;

2) А(ВС) = (АВ)С;

3) a(АВ) = (aА)В = А(aВ);

4) (А₁ + А₂)В = А₁В + А₂В, А(В₁ + В₂) = АВ₁ + АВ₂;

5) А0 = 0А = 0;

6) (АВ)^т = А^тВ^т.

При умножении двух ненулевых матриц может получиться нулевая матрица.

Данный текст является ознакомительным фрагментом.