12. Ряд. Сумма ряда. Сходимость ряда. Арифметические действия над рядами. Ряды с положительными членами

Числовым рядом называется выражение 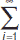a_i = а₁ + а₂ +…+ а_n +…, где a_i (i= 1, 2…, n…) – вещественные или комплексные числа.

Частичной суммой ряда (n–ой частичной суммой) называется число S_n = а₁ + а₂ +…+ а_n = 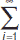a_i.

Из частичных сумм можно образовать последовательность S₁ = a₁, S₂ = a₁ + a₂, S₃ = a₁ + a₂ + a₃ и т. д. Если существует предел последовательности частичных сумм ряда, то ряд называется сходящимся, а сам предел называется суммой ряда, обозначается . Если такового предела не существует, то ряд называется расходящимся.

Теорема. На сходимость ряда не влияет отбрасывание конечного числа его членов. Если ряд сходится, то его n–ый член стремится к нулю при неограниченном возрастании n, т. е. 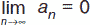. Пусть даны два ряда 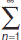a_n и 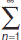b_n. Тогда в результате сложения этих двух рядов получится ряд 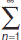(a_n + b_n), при умножении получается ряд 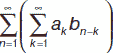, произведением ряда 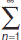a_n на число с будет ряд 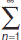ca_n (с – вещественное или комплексное число).

Теорема. Пусть даны два ряда, имеющие соответствующие суммы 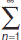a_n = S₁ и 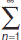b_n = S₂. Тогда справедливо: 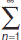(a_n +b_n) = S₁ +S₂, 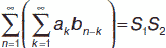, 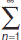ca_n = cS₁ (где с – число).

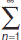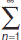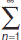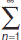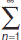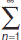Теорема (принцип сравнения). Пусть даны два ряда с положительными членами a_n и b_n. Если ряд a_n сходится и a_i ? b_i (i = 1, 2…, n), то и ряд b_nb_n сходится, причем a_n ? b_n.

Теорема. Если члены ряда 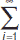a_i не меньше соответствующих членов расходящегося ряда 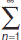b_n, то и ряд 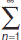a_n расходится.

Данный текст является ознакомительным фрагментом.