1.2. Процентные платежи как форма денежных потоков

В зависимости от условий проведения финансовых операций как наращение (будущая стоимость), так и дисконтирование (приведенная стоимость) могут осуществляться с применением простых, сложных и непрерывных процентов. Их использование возможно только после четкого определения следующих составляющих:

– суммы денежных средств, о которых может идти речь;

– время, когда эти суммы должны быть выплачены или получены;

– осознанные риски, связанные с инвестированием;

– соответствующая ставка дохода (ставка процента или дисконта) с учетом рыночных условий и оцененного риска.

Простые проценты – это проценты, которые выплачиваются (приносятся) лишь на исходную или основную сумму, взятую (или отданную) в долг. В частности И. А. Бланк дает следующее определение: «Простым процентом называется сумма дохода, начисляемого к основной сумме инвестированного капитала в каждом интервале времени, по которой дальнейшие расчеты платежей не осуществляются»31. Аналогичное определение дают Джеймс К. Ван Хорн и Джон М. Вахович, мл.: «Простые проценты (simple interest) – это проценты, которые выплачиваются (или приносятся) лишь на исходную, или основную, сумму (principal), взятую или отданную в долг»32. Таким образом, денежное выражение простых процентов является функцией трех переменных: исходной или основной, суммы, взятой (или отданной) в долг; процентной ставки за один период времени; и количества периодов времени, на которые основная сумма берется (или отдается) в долг.

Формула для вычисления простых процентов имеет следующий вид:

где S(r) – простые проценты в денежном выражении;

P0 – основная или исходная сумма, заимствованная (или одолженная) в первоначальный момент времени (в точке (о) в начале первого периода);

r – процентная ставка за один период времени;

n – количество периодов времени.

Чтобы определить будущую (или конечную) стоимость суммы сделки на конец периода добавляют проценты, заработанные на основную сумму, к инвестированной исходной сумме.

Как правило, простые проценты используются в краткосрочных финансовых операциях, срок проведения которых меньше или равен году. Базой для исчисления процентов за каждый период является первоначальная сумма сделки, что видно из схемы простых процентов, представленной на рис. 6.

Рис. 6. Схема простых процентов33

Если продолжительность краткосрочной операции меньше года (т. е. t), то

Дисконтирование – узловое понятие в современной теории инвестиционного анализа. Это тип финансового расчета, применяемый для определения ценности будущих приходов и расходов денег с учетом сокращения их реальной стоимости по сравнению с текущим моментом.

Смысл дисконтирования заключается в том, что текущая стоимость будущих финансовых потоков может существенно отличаться от их номинальной стоимости. Дисконтирование является важнейшим механизмом, позволяющим представить финансовое положение организации достоверно. В частности, это одна из самых сложных технических проблем, с которыми сталкивается российский бухгалтер при подготовке отчетности по МСФО. В МСФО дисконтирование может повлиять на балансовую стоимость любого элемента учета и тем самым изменить финансовые результаты компании.

Дисконтирование (встречается название математическое дисконтирование) предполагает, что в качестве нормы приведения используют ставку r, применяемую при наращении. Таким образом, математическое дисконтирование представляет собой задачу, обратную наращению (см. выше) и сводится к определению PV по известным значениям FV, r, n.

Из зависимости (5)

Из зависимости (6)

Разность (FV – PV) называют дисконтом. Используемую при этом норму приведения r – декурсивной ставкой процента.

Сам термин «простые проценты» – неудачный перевод с английского, на практике это следует понимать как упрощенный (приближенный) способ расчета сложных процентов. По мнению В. И. Решецкого: «В современных условиях при широкой доступности калькуляторов (и компьютеров) надобность в простых процентах полностью отпала, поскольку все расчеты можно делать точно, и эту культуру финансовых отношений необходимо внедрять в современной России»34.

Большинство операций в финансах, связанных со стоимостью денег во времени, не имеет вообще никакого отношения к простым процентам. Обычно в таких ситуациях используются сложные проценты. Концепция сложных процентов имеет большое значение для понимания всей финансовой математики.

Обратимся к определению, которое дает И. А. Бланк: «Сложным процентом называется сумма дохода, начисляемого к основной сумме инвестированного капитала в каждом интервале, которая не выплачивается, а присоединяется к основной сумме инвестированного капитала и в последующем платежном периоде сама приносит доход»35.

Аналогичное определение дают Джеймс К. Ван Хорн и Джон М. Вахович, мл.: «Сложные проценты – проценты, выплачиваемые (приносимые) на любые, ранее выплаченные (принесенные) проценты, а также на основную сумму долга, взятую (или отданную) в долг»36. Таким образом, суть сложных процентов в том, что проценты, выплачиваемые (приносимые) по займу (инвестиции), периодически добавляются к основной сумме. Имеет место эффект «процентов на проценты», что представлено на рис. 7.

Рис. 7. Схема сложных процентов37

Сложные проценты применяются в финансовых операциях, которые превышают один год. Вместе с тем они могут использоваться и в краткосрочных финансовых операциях, если это предусмотрено условиями сделки, либо вызвано объективной необходимостью (например, высоким уровнем инфляции, риска).

Чтобы определить будущую (конечную) стоимость, расчет делают по следующим формулам.

Если проценты начисляются один раз в год, то:

Данная формула является базовой, описывающей накопленную сумму единицы.

Все другие факторы производны от базового уравнения. Каждый из них предусматривает, что процент приносят деньги, находящиеся на депозитном счете, причем только до тех пор, пока они остаются на счете, т. е. учитывает эффект сложного процента, который будучи полученным переводится в основную сумму.

Период накопления может быть и более коротким, чем год (например, месяц, квартал, полугодие, т. е. m – раз в год). Это фиксированное (дискретное) накопление.

если проценты начисляются m – раз в год:

Определение текущей стоимости единицы (приведенной стоимости или дисконтирование) – действие обратное начислению сложных процентов. Это сегодняшняя стоимость единицы, которая должна быть получена в будущем при заданном периоде n и процентной ставке r.

из зависимости (9)

из зависимости (10)

В практических расчетах применяются так называемые дискретные проценты, т. е. проценты, начисляемые за фиксированные интервалы времени (год, полугодие и т. д.). Иначе говоря, время рассматривается как дискретная переменная. В некоторых случаях – в доказательствах и аналитических финансовых расчетах, связанных с процессами, которые можно рассматривать как непрерывные, в общих теоретических разработках и значительно реже на практике – возникает необходимость в применении непрерывных процентов, когда наращение или дисконтирование производится непрерывно, за бесконечно малые промежутки времени. В подобных ситуациях применяются специальные непрерывные процентные ставки.

Следует добавить, что при последовательном погашении задолженности возможны два способа начисления процентов. Согласно первому процентная ставка (простая или сложная) применяется к фактической сумме долга. По второму способу простые проценты начисляются сразу на первоначальную сумму долга, без учета последовательного его погашения. Последний способ применяется, например, в потребительском кредите.

Важным применением концепции приведенной стоимости является определение размера платежей, которые требуются для погашения постепенно выплачиваемого займа, так называемая амортизация займа. Амортизация займа связана с определением периодических платежей, необходимых для исчисления основной суммы займа к моменту, когда наступит срок полного его погашения; при этом должна также обеспечиваться выплата процентов по невыплаченной части основной суммы займа.

Джеймс К. Ван Хорн и Джон М. Вахович, мл. обращают внимание на то, «что часть платежа, приходящаяся на выплату процентов по займу, с течением времени уменьшается, тогда как часть платежа, приходящаяся на выплату основной суммы займа, увеличивается»38. Соотношение между процентом и основной суммой займа очень важно, поскольку налог на прибыль уменьшается лишь на суммы процентов по долгу.

Любая финансовая операция характеризуется и может быть полностью описана посредством порождаемых ею денежных потоков. В целом сущность анализа финансовых операций заключается в определении времени и сумм, генерируемых ими платежей и последующей их оценки в виде показателей, позволяющих сравнить и сопоставить альтернативные варианты.

Понятие «денежный поток» (cash flow, CF – поток наличности, поток платежей) является фундаментальным в финансовом менеджменте, поэтому весьма важным является его однозначное толкование экономистами различных специализаций. Вместе с тем Валерий Галасюк обнаружил, что понятие денежного потока (cash flow), широко используемое в финансовом менеджменте на протяжении многих десятков лет, по своему содержанию отличается от содержания понятия денежного потока, приведенного в МСФО 7 «Отчет о движении денежных средств». МСФО 7 следующим образом определяет основные элементы понятия денежного потока: «Денежные потоки – это приходы и выбытия денежных средств и их эквивалентов»39. Таким образом, МСФО 7 трактует понятие «денежные потоки» в относительно узком смысле, так как инвестиция рассматривается, как правило, как эквивалент денежных средств только в случае короткого срока ее погашения.

Рассмотрим трактовки понятия «денежный поток» специалистами по финансовому менеджменту. Р. А. Брейли и С. С. Майерс дают следующее определение: «Поток денежных средств от производственно-хозяйственной деятельности определяется вычитанием себестоимости проданных товаров, прочих расходов и налогов из выручки от реализации»40. И. А. Бланк дает следующее определение денежному потоку: «Денежный поток – поступление (положительный денежный поток) и расходование (отрицательный денежный поток) денежных средств в процессе осуществления хозяйственной деятельности предприятия»41. Г. Б. Поляк предлагает трактовать денежный поток как в широком, так и в узком смысле.

«Под денежным потоком или потоком наличности в широком смысле понимается распределенное во времени движение денежных средств, возникающее в результате хозяйственной деятельности субъекта»42. То есть денежный поток – это множество распределенных во времени выплат (оттоков) и поступлений (притоков), понимаемых в широком смысле. В качестве элемента денежного потока может выступать доход, расход, прибыль, платеж и др.

В практической деятельности объектами анализа служат потоки платежей, генерируемые тем или иным активом, их комбинацией (портфелем) либо инвестиционным проектом. В этом смысле менеджеру или аналитику, на наш взгляд, удобнее оперировать более конкретным (узким) понятием, которое было сформулировано Г. Б. Поляком в следующем виде.

«Под денежным потоком понимается распределенная во времени последовательность выплат и поступлений генерируемая тем или иным активом, портфелем активов, инвестиционным проектом в течение операции»43.

В дальнейшем, говоря о денежных потоках, мы будем рассматривать их именно в этом смысле, т. е. в контексте приведенного определения.

Денежный поток обладает рядом характеристик, которые представлены на рис. 8.

Получаемые платежи или поступления называют притоками (cash inflows – СIF), выплачиваемые – оттоками (cash outflows – COF) денежных средств. Разница между положительным и отрицательным денежным потоком называется чистым денежным потоком.

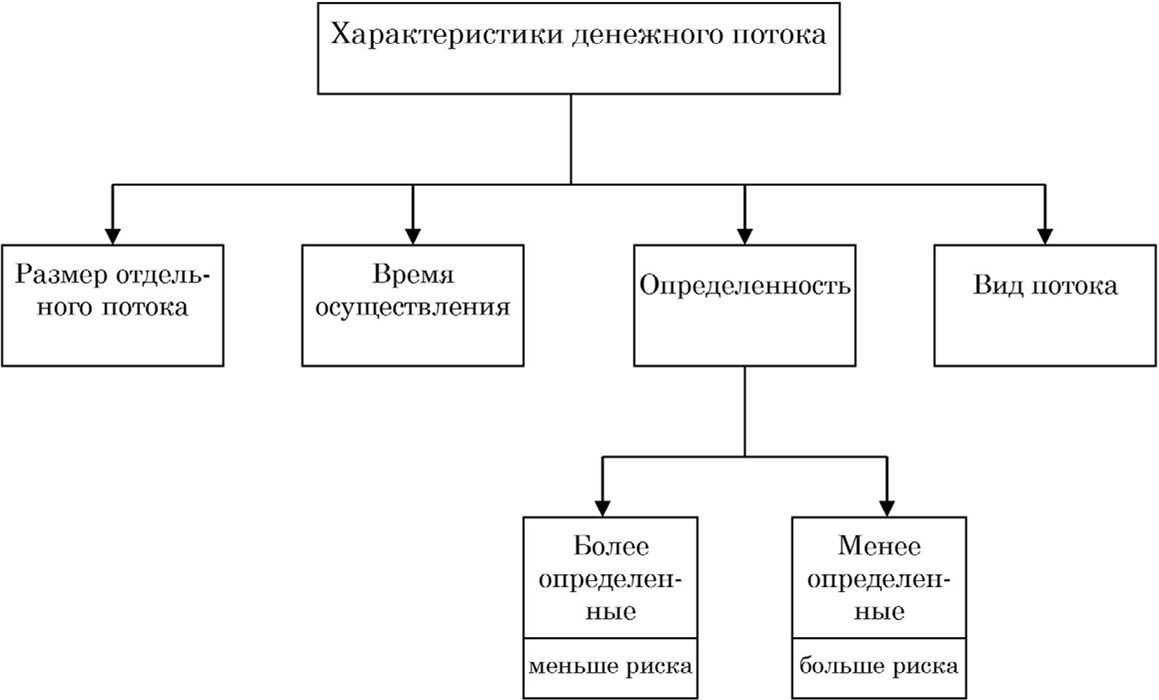
Рис. 8. Характеристики денежного потока44

Размеры выплат и поступлений (т. е. отдельных элементов денежного потока) могут быть известны с той или иной степенью определенности. Чем более определенны суммы платежей, тем меньше риск, связанный с соответствующей операцией.

Разнообразие хозяйственных операций в условиях рынка обусловливает существование самых различных видов денежных потоков. В этой связи возникает необходимость в их классификации.

Основные классифицирующие признаки и соответствующие им виды потоков платежей приведены в табл. 2.

Таблица 2

Классификация потоков платежей 45

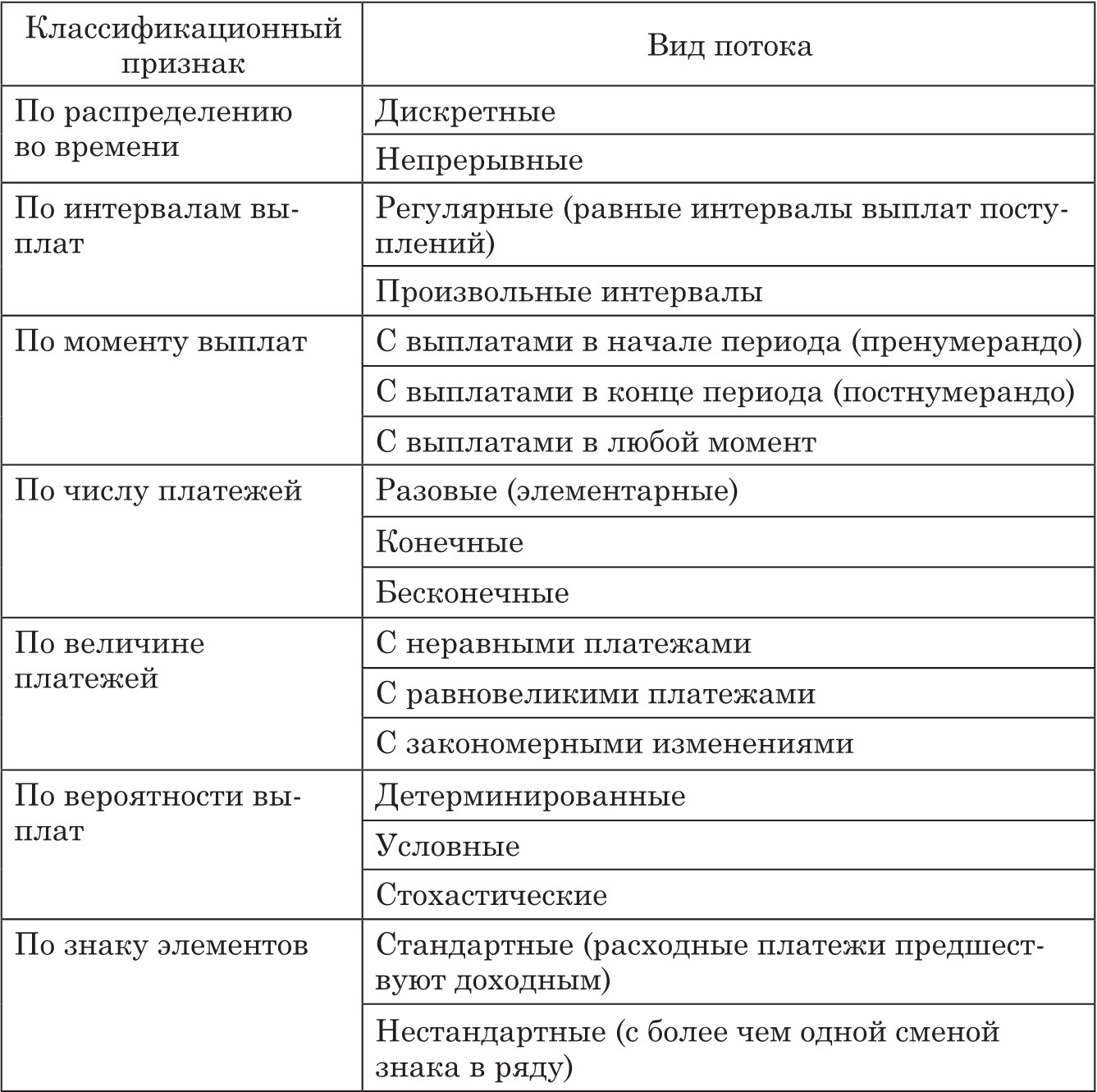
Кроме того, различают:

– релевантные (relevant cash flows, RCF) денежные потоки – это инкрементальные свободные денежные потоки, которые компания может предполагать в случае реализации проекта;

– инкрементальные (приростные, incremental cash flows, ICF) денежные потоки представляют собой изменения уже существующих денежных потоков фирмы, возникающие после принятия проекта;

– свободные денежные потоки (free cash flow, FCF) – это количество денежных средств, оставшихся после того, как компания осуществит все инвестиции в активы, необходимые для поддержания ее операций.

Ю. Бригхэм и М. Эрхардт делают следующее заключение: «Таким образом, свободное движение денег представляет собой финансовые ресурсы, действительно доступные для распределения между инвесторами. Следовательно, способ, которым менеджеры могут повысить ценность своих фирм для них, – это увеличить свободный поток денежных средств»46.

«Чистый денежный поток (чистое движение денежных средств) (Net cash flow, NCF) = (Чистая прибыль – неденежные доходы + неденежные затраты). Амортизация обычно является самой крупной неденежной статьей затрат, поэтому чистый операционный денежный поток часто рассчитывается как чистая прибыль плюс амортизация»47.

Простейший элементарный денежный поток состоит из одной выплаты и последующего поступления, либо разового поступления с последующей выплатой, разделенных n периодами времени (например, срочные депозиты, обязательства с выплатой процентов в момент погашения, некоторые виды страховок, ценных бумаг и др.). Несмотря на разнообразие хозяйственных операций, наибольшее распространение на практике получили некоторые частные случаи дискретных денежных потоков. К важнейшим из них следует отнести элементарные (двухпериодные) и регулярные (многопериодные) конечные потоки платежей. Частным случаем денежного потока являются аннуитеты. Аннуитет или финансовая рента – это серия равновеликих, равномерных (через равные промежутки времени) денежных потоков. Аннуитеты могут быть:

– срочные – это когда число равных временных интервалов ограничено;

– бессрочные (вечные) – если срок аннуитета не ограничен. Такой аннуитет называют перпетуитетом;

– простой аннуитет, обычный или отсроченный (постнумерандо) – когда платежи осуществляются в конце временных интервалов;

– авансовый или ускоренный аннуитет (пренумерандо) – когда платежи осуществляются в начале временных интервалов.

Количественный анализ денежных потоков, генерируемых за определенный период времени хозяйственной операцией, в общем случае сводится к исчислению: FV – будущей стоимости потока за n периодов и PV – современной стоимости потока за n периодов.

Часто возникает необходимость определения и ряда других параметров операций, важнейшие среди которых CFt – сумма платежа в периоде t, г – процентная ставка, n – число периодов проведения операции. Существуют различные формулы для нахождения значений будущей и приведенной стоимости как смешанных (неоднородных) денежных потоков, так и аннуитетов. Порядок расчета не вызывает сомнений (точка зрения на него единая и рассматривается многими авторами, как отечественными, так и зарубежными), поэтому не будем на нем останавливаться.

Важным практическим применением теории аннуитетов является составление различных вариантов (планов) погашения задолженности. При составлении плана погашения интерес представляют размеры периодических платежей заемщика – выплаты процентов и выплаты по погашению основной суммы долга – при различных условиях погашения.

Нетрудно заметить, что величины FV в операциях наращения, и PV в операциях дисконтирования зависят:

– от времени получения;

– от значения процентной ставки r.

Обобщая изложенный материал, перечислим основные способы анализа временной стоимости денег:

– наращение по схемам простого или сложного процента;

– нахождение текущего, приведенного значения будущего потока денежных средств или ряда таких потоков (дисконтирование);

В итоге следует заметить, что большинство финансовых операций включают ситуации, когда участники сделок осуществляют платежи в одни моменты времени, но получают возмещения в другие. Суммы в денежном выражении, уплачиваемые или получаемые в эти моменты, отличаются друг от друга, и их приходится сравнивать методами анализа временной стоимости денег (time value of money, TVM), используя сложные проценты) В настоящее время в основе базовых оценочных критериев эффективности финансовых операций, таких как чистая приведенная стоимость, внутренняя норма доходности, лежат операции дисконтирования. Фактор времени, таким образом, учитывается через операции дисконтирования. В наших исследованиях были рассмотрены операции наращения не потому, что они являются основой для математического дисконтирования, т. е. не для того, чтобы соблюсти приличия. Операции наращения при построении критерия внутренней нормы доходности инвестиций являются такими же равноправными участниками расчета, как и операции дисконтирования.

Данный текст является ознакомительным фрагментом.