Глава 14 Космос как число

В последние месяцы своего пребывания в Кротоне пифагорейцы продолжали искать решение для описания мироздания, сохраняя безразличие ко все нарастающей буре народного негодования, направленного против секретности и исключительности. Не обращая внимания на Килона и его демократически настроенных бунтовщиков,

братство продолжало разрабатывать свою неземную теорию, словно впереди была целая вечность, не осознавая, что в их распоряжении осталось всего несколько недель, чтобы завершить решение задачи. Возможно, они проявили мудрость и тут. Все, что они успели закончить и передать своим интеллектуальным последователям, оказалось менее ярким и побуждающим к мысли, чем бездна беспорядочных, причудливых умозрительных построений, которые они оставили на полпути. Родственные им души все еще продолжают искать вдохновение в незавершенных делах пифагорейцев. Другие же предаются сожалению, что Килон и его толпа не сумели добраться до всех колоний, где осели пифагорейцы, чтобы так же истребить их, как они истребили материнскую организацию в Кротоне. Более объективные критики, даже не воспринимающие учения Пифагора, просто перечисляют, что распространяло братство именем разума, и предоставляют возможность фактам говорить самим за себя. Об этом беспристрастно судил Аристотель, живший в 384–322 годах до н. э., всего два с половиной века спустя после Пифагора. Его оценки наиболее исчерпывающие. «Они занимались исключительно математикой, которую они впервые начали развивать. Пифагорейцы додумались до принципов математики, которые оказались аналогичными для других областей знания».

Само по себе это изречение ошеломляет. Но Аристотель, не будучи фанатиком математики и не выказывая своего отношения к предмету, посчитал необходимым остановиться на отдельных деталях.

«Поскольку числа, естественно, стоят выше всего остального, пифагорейцы сделали допущение, что они могут установить более тесные аналогии между числами и предметами, чем между огнем, землей или водой (три элемента из четырех у Эмпедокла) и предметами. Таким образом, справедливость стала одной комбинацией чисел, знания и разум – другой, возможность – третьей и т. д.»

«Опять же, они рассматривали возможность выражения составных частей… музыкального ряда в виде чисел.

Потому что все остальное, казалось, имеет форму чисел, и, поскольку числа в природе, как кажется, предшествуют появлению предметов, они на этом основании пришли к выводу, что природа чисел идентична природе предметов, следовательно, небеса создали число и гармонию».

«Указав на тесные аналогии между числами и астрономическими явлениями и, действительно, между числами и всеми явлениями целого космоса, они выстроили систему в астрономии. Если в системе возникали нестыковки, они прилагали все силы на нахождение связи (между числами и наблюдаемыми явлениями в астрономии). Например, поскольку «десять» казалось им числом совершенства, они утверждали, что существует десять небесных тел (включая сферу «неподвижных» звезд). В видимой части было только девять, они допустили существование десятой – Контр-Земли, чтобы отбалансировать Землю. …они заявили, что число есть прародитель предметов и причина как их материального существования, так и изменений и различных состояний…»

Это до некоторой степени язвительное обобщение всеобъемлющего решения пифагорейцев для описания мира переполнено наполовину скрытыми упоминаниями, что учение следует воспринимать по частям, чтобы раскрыть его треклятую законченность. Дабы быть кратким, нумерологическая нить, связывающая все отдельно существующие части в компактное единое целое, не вызывает сомнений, например 10 = 1 + 2 + 3 + 4. Каждое из чисел 1, 2, 3, 4, 10 в этом базовом отношении совпадения пифагорейской нумерологии имеет не просто одно значение или даже два, а буквально дюжины значений, ни одна пара из которых не имеет между собой ничего общего.

Если сказанное кажется полностью лишенным смысла для создания рациональной системы мира, то можно смягчить грубость любого порицания обращением к аналогии с современной физикой, нам же следует вернуться к естествознанию наших предков. Рассматривая каждый из нескольких прогрессивных научных трудов по разным направлениям классической физики: механики, теплопроводности, акустики, оптики, электричеству и магнетизму, замечаем, что два и более из них содержат как минимум одну пару практически идентичных равенств. Исключением могут являться буквы, которыми они записаны. Теперь, если конкретное равенство появляется, скажем, как в теории электромагнетизма, так и в теории упругости, данный феномен электромагнетизма может быть описан на языке эластичности, с которым, возможно, мы лучше знакомы. Или если равенства, суммирующие вибрации эластичного твердого тела, появляются в теории света, то можно описать свет как вибрацию гипотетического эластичного материала и назвать этот материал универсальным эфиром. Следуя этой логике, можно даже убедить самих себя в том, что этот эфир существует по-настоящему, как и осязаемый кусок сапожной ваксы. Все это в значительной степени тривиально. Но вера, которая это породила, не является ни тривиальной, ни устаревшей. Она живее и плодороднее в плане новых знаний, чем когда-либо в прошлом, и, как и во времена Пифагора, продолжает предсказывать как проверяемый факт, так и не подлежащий проверке миф. Такая вера – просто убеждение, что возможно до определенной малой степени предсказывать знания и предвидеть будущее материального мира. Древняя магия утверждала, что в состоянии это сделать, но никогда не делала. Менее древняя астрономия достигла значительных успехов. Современная наука имела больше успехов, чем поражений, в своих наиболее успешно развивающихся областях, в частности в физике, астрономии, генетике, и в достижении результатов, как успешных, так и разгромных, математические умозаключения сыграли впечатляющую роль.

Подчас, как в теории относительности, так и в современной квантовой теории, успешные предсказания удивляют даже людей, сделавших их. Когда-то успешность предсказания подтвердило открытие планеты Нептун в 1846 году, ставшее результатом математического анализа орбиты Урана. Математики подсказали астрономам, где искать новую планету, и она была найдена. Событие стало триумфом математики и закона всемирного тяготения Ньютона. Нумерология в теории Пифагора о Солнечной системе предсказала существование Антипода, который, разумеется, нельзя было рассмотреть на небесах и никогда не найти в будущем. Но вера, побудившая на предсказание, была той же, что и в случае с Нептуном. Недавний пример (1918) подобной веры в предсказании столь же ошибочен, как и в случае с Антиподом: красивая и разумная модификация основной теории относительности позволила предсказать, что атомы химических элементов должны обладать схожими характеристиками. Наблюдаемое отсутствие указанных характеристик отнесло предсказание в ту же категорию, как и у Антипода. При наличии подобных параллелей между естествознанием прошлого и естествознанием настоящего, порождающих глубокие тайны, необходимо рассмотреть несколько примеров «сущего» в пифагорейском «Все сущее есть число». Если какой-нибудь современный ученый ожидает или надеется на симпатии со стороны своих коллег в следующем столетии, то не станет презирать коллегу за преждевременную попытку (не забывайте, предпринятую двадцать пять веков тому назад) дать рациональное объяснение космосу, а проявит учтивость и удивительную толерантность.

Сердцем и умом пифагорейского космоса были декады и тетрады. Декады состояли из первых десяти натуральных чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, а тетрады – из первых четырех 1, 2, 3, 4.

Можно подчеркнуть вначале, что 1 иногда означала достоинство быть числом вообще. Но когда некие значительные обобщения требовали от 1 стать числом, дабы избежать вызывающих раздражение противоречий, 1 на время становилась таким же числом, что и остальные.

Хотя этот двойственный подход лишил 1 некоторых нумерологических привилегий, недостаток вполне можно было компенсировать приписыванием дополнительных полномочий, которых нет ни у одного из других чисел.

Поскольку 1 очевидно является автором и прародителем как тетрад, так и декад: 2 = 1 + 1; 3 = 2 + 1 = 1 + 1 + 1 и так далее, такая 1 может быть идентифицирована как универсальная и всемогущая Единица – создатель всего сущего, когда становится ясно, что все во вселенной создано, или выражено, в декадах. Следует признать неопровержимость данной логики.

В действительности из тетрад достаточно получить столько, сколько может быть задумано, поскольку тетрады порождают или создают декады: 2 = 1 + 1; 3 = 1 + 2; 4 = = 2 ? 2; 5 = 2 + 3; 6 = 2 ? 3; 7 = 3 + 4; 8 = 2 ? 4 = 2 ? 2 ? 2; 9 = 3 ? 3; 10 = 1 + 2 + 3 + 4. Представлены только некоторые из всего множества различных декад. Выбранные декады самые важные для пифагорейцев. Другими столь же значимыми были: 5 = 2 + 1 + 2; 7 = 3 + 1 + 3; 9 = 4 + 1 + 4, где очевидны общие характеристики. Следует заметить, что ни одно четное число не может быть разложено на сумму из трех чисел, из которых среднее есть 1, а первое и последнее равны между собой. Банально? Совсем нет. Данный трюизм элементарной арифметики проявится метафизической нумерологической сущностью Ограниченного и Неограниченного, Конечного и Бесконечного, Времени и Вечности, которые в течение прошедших двух тысяч лет, безусловно, находятся среди вопросов, наиболее часто становившихся объектами обсуждения среди метафизиков. Если все сущее есть число, что же такого потрясающего или удивительного мы находим в том, что метафизика есть разновидность мистической арифметики? Непосвященным кажется довольно странным, что числа более десяти высокомерно отвергаются. Но в действительности это не так. Согласно наблюдениям Пифагора, «декады содержат в себе все сущее, поскольку числа более декад просто повторяют первые десять». Мысль заключается в следующем: 11 = 10 + 1; 12 = 10 + 2… 19 = 10 + 9; 20 = 2 ? 10; 21 = 2 ? 10 + 1;…29 = 2 ? 10 + 9;… и т. д. Нумеролог из Вавилона сделал бы все числа сверх 60 отголоском истины, заключенной в числах от 1 до 60. То, что придумали пифагорейцы, равнозначно специальным методам, которыми пользуются в современной высшей арифметике. Они делили все натуральные числа на десять классов. Первый класс включал в себя все натуральные числа, которые давали в остатке 1, когда их делили на 10, второй класс включал в себя те, что давали в остатке 2, когда их делили на 10, и так далее вплоть до десятого класса, который включал все натуральные числа, которые делились на 10 без остатка. С позиций нумерологии было не обязательно относиться по-разному к числам в любом из десяти классов, потому что все они, согласно гипотезе, были, с позиции нумерологии, неотличимы.

Следующее фундаментальное допущение пифагорейцев лежит так глубоко, действительно глубоко, что цивилизованный человек едва ли может надеяться вытащить его на свет разума. Нечетные числа мужского рода, а четные числа – женского. Можно только задать вопрос почему, не ожидая ответа, за исключением, возможно, неуверенного упоминания исчезнувшего фаллицизма или забытого орфизма. Примитивные люди, кажется, были даже более педантичны, чем некоторые из современных, в отношении секса, зачастую включая его физически и духовно в свои верования. Возможно, мужская 1 и женская 2 были святынями из забытых обрядов. Каким бы ни было происхождение физиологической арифметики, она оказалась важна для пифагорейской теории мира.

Исходя из постулата, что существуют числа противоположного пола, следует (согласно пифагорейцам), что для брака число 5 – мужское, число 6 – женское, и оба числа отступают, как и должны, в полноценной декаде. Рассуждения просты. В законном браке одна женщина соединяет свою жизнь с одним мужчиной. Но 2 – это первое женское число, а 3 – первое определенно мужское число. Это один из нумерологических случаев, когда 1, хотя и нечетному числу и по этой причине предположительно мужскому, отказано в привилегиях, данным другим числам. Сложение 2 и 3 есть 2 + 3, или 5, что означает мужское свадебное число. Но ему разумно должно составлять пару женское число. Поскольку в свадьбе женщина усилена мужчиной: 2 ? 3 = 6.

Если же спросить, почему не 3 + 4, или 7, стало символом мужской свадьбы вместо 2 + 3, Пифагор ответил бы, что 4 есть справедливость, а справедливость добродетель для мужчин, а не для женщин, поэтому правильно дать браку мужское число 3. Слегка надавив на него, узнаем, почему 4 есть справедливость. Получаем легкий ответ: 4 = 2 ? 2 = 2 + 2, где просто на миг не обращают внимания, что 2 – женское число. Но какой бы ни был пол у 2, как и 4 = 2 ? 2 = 2 + 2 означает «возврат взаимной любви» или, в более конкретном выражении, «око за око и зуб за зуб» – один из неизменных канонов любой дикарской справедливости. К тому же, где бы оно ни появлялось, число 7 есть девственность, а по этой причине не подходит на роль мужского свадебного числа.

Мы находимся в мире фантазий, где все, что ни пожелаешь доказать, можно доказать, и по уважительной причине любое препятствие на пути прямой дедукции может быть устранено введением нового постулата, отменяющего препятствие. Наши созидательные силы безграничны. Ничто не может препятствовать нам, потому что никогда мы не подвергнем наши выводы радикальной проверке репродуктивного опыта в мире чувств. Действительно, они выше любой подобной проверки. Наше раздумье, создание свободного разума, строго рационально вне зависимости от того, есть ли у него противоположность в повседневном мире чувственных ощущений. Если последовать за Пифагором и Эмпедоклом и высказать постулат, что только думающая часть души может открыть истину человечеству, следует поверить Платону, что наш выдуманный мир реален, а все остальное – иллюзия.

Включившись в дело порицания пифагорейцев за манипулирование своими постулатами, стоит им только наткнуться на трудности в своей дедуктивной нумерологии, следует вспомнить, что подобная практика отнюдь не редкость для современной науки. Рассмотрим простой и частый пример: амбициозный математик взялся за нерешенную задачу. Решение этой задачи станет существенным прорывом в науке. Но после нескольких месяцев тяжелого труда он устанавливает, что реальная задача выше его сил. Поэтому он возвращается в самое начало, вносит едва заметное изменение в одно из данных условий задачи, которое блокировало каждый его шаг, и дальше продолжает без проблем. Он затем пытается убедить себя, что легкая задача, которую он решил, есть не менее значительный вклад в науку, чем та сложная, от решения которой он отказался. Чтобы не вызывать негативной реакции ссылкой на конкретные примеры современности, вернемся к первым великим мастерам в искусстве подмены трудного легким.

Дабы закруглиться с нумерологией Пифагора по вопросам брака, обратимся к детям. Сейчас почти каждый, кто манипулирует числами, сталкивается с замечательными особенностями 6 – числа женского замужества, совсем как пифагорейцы наткнулись на него в начале своей деятельности: 6 = 1 + 2 + 3. Но 1, 2, 3 есть числа меньше 6, на которые оно делится без остатка, и число 6 есть сумма всех своих делителей, которые все меньше его. По этой причине пифагорейцы нарекли число 6 совершенным числом. Такие числа встречаются очень редко, и их трудно отыскать, и до сих пор неизвестно, существует ли нечетное совершенное число. Следующее после 6 совершенное число 28, потому что 28 = 1 + 2 + 4 + 7 + 14, и 1, 2, 4, 7, 14, все они являются делителями 28, меньшими, чем само число 28, следующее число 496; за ним 8128.

В совершенстве 6 = 1 + 2 + 3 Пифагор видел временно мужскую 1, соединенную с постоянно женской 2 и вечно мистической 3 в совершенном браке. Почему 3? Потому что 3 первое, самое привычное и самое распространенное из всех неисчислимых троиц, которое доминирует в религиях с самого возникновения истории, в частности: человеческая троица, состоящая из отца, матери и ребенка, – 1, 2, 3. Но это не все. Ребенок есть результат единения отца и матери: 3 = 1 + 2. Все это, без сомнения, просто фантазии, до тех пор пока мы отрицаем их пафос. Число 3 символизирует вечную троицу, и трогательно сознавать, что ранние нумерологи, видимо, наделяли временную человеческую радость стабильностью, которую они хотели бы видеть в ней.

К слову сказать, число 3, являющееся первым мужским числом, может быть мужчиной. В мужчине по этой причине проявляется нечто божественное, поскольку число 3 – это и Святая троица. Таков пример дедукции, обнаруживаемый в раннехристианской нумерологии. Пифагорейцы пришли к еще более занимательному выводу, связанному с отождествлением числа 3 с человеком. Ничто в человеческом опыте не бывает более бесспорным, чем печальный факт, что жизнь человека проходит три фазы: юность, зрелость и смерть. А число 3 – единственное число, в котором начало и конец даже равны средней части: 3 = 1 + 1 + 1. Итак, мужчине уготовано судьбой родиться, мужать и умереть, что точно соответствует числу 3, которым он и является. Даже Аристотель, при всем своем практичном превосходстве над вводящими в заблуждение пифагорейцами, клюнул на приманку нумерологии в своем трактате «Поэтика», как и во многом другом. Его требование, чтобы трагедия состояла из трех частей: вступления, основной части и финала, – есть проявление чистейшей воды нумерологии. Так сказал сам учитель!

Совершенство 28 значительно выше, чем совершенство 6 с позиции космической истинности, но следует при этом кое-что учитывать. Неделя состоит из 7 дней, 14 – две недели, а 28 – лунный месяц, 1 и 2 – мужчина и женщина или Бог и женщина, 4 – справедливость, а 7 – «чистое число», обозначенное так потому, что 7 не создает чисел внутри декад ни путем умножения, ни путем деления, являясь суммой 1, 2 и 4. И так далее. Почти что «сущее»: от человека до луны справедливо (четверливо) одно совершенство.

В своем обзоре древней нумерологии Аристотель заметил, что «справедливость стала одной комбинацией чисел, образованность и мудрость – другой, возможность – третьей и т. д.».

Мы видели, как число 4 означает справедливость. Было бы интересно взглянуть на понятия «мнение» и «знание». Хотя Аристотель специально не упоминает их, они сродни абстракциям в его изложении. Многое из того, о чем Платон и Сократ (говорящий то, что Платон вложил в его уста) говорили по поводу мнения и знания, было позаимствовано у первых нумерологов.

Наше знакомство с лабиринтом философской арифметики началось с двойной двери Ограниченного и Безграничного – тех мистических абстракций, которым суждено было стать альфой и омегой метафизики от Платона до Гегеля и математики от Пифагора до Кантора, жившего в 1845–1918 годах основателя современной теории математической бесконечности.

Нечетные числа в пифагорейской нумерологии ограничены, конечны и детерминированы, даже числа, не подпадающие под эти мужские качества решимости. Значения технических терминов в данной работе отличны от тех значений, которые употребимы в наши дни. Так, «конечный» означает имеющий границы, или завершение, а «бесконечный» означает неограниченный, незавершенный. И «конечный» и «бесконечный» встречаются в современной математике с такими же дефинициями, но они не соответствуют этим терминам в пифагорейской нумерологии и даже близко не напоминают вложенный в них смысл.

В пифагорейской попытке дать рациональное знание «конечность» нечетных чисел и «бесконечность» четных чисел отражают два элементарных понятия, тривиальные для нас. Нечетное число 5, например, может быть представлено в виде суммы двух равных чисел и единицы, а единица может быть расположена в центре равенства: 5 = 2 + 1 + 2. То же самое справедливо для 7 = 3 + 1 + 3, при этом общее нечетное число можно записать как n + 1 + n. Созидательная Единица, 1, «ставит рубеж», или «ограничивает» два равных числа. Аналогичное разделение мужских чисел женским числом 2 невозможно, поскольку нечетное число, деленное на 2, дает остаток (¹/₂), не являющийся целым числом. Следовательно, с точки зрения нумерологии женское число может разделить два мужских, но никогда одно.

Четное число, наоборот, не ограничено в своей внутренней структуре божественно созидательной Единицей. 4 = 2 + 2; 6 = 3 + 3;…2n = n + n. Следовательно, женские числа могут быть разделены наименьшим из них (2) на 2 целых числа. Возможная скрытая особенность состоит в применении «ограниченного» и «безграничного», которые будут рассмотрены в следующем разделе, где будет показано, что «линия» есть понятие, «ограниченное» своими концами, которыми выступают точки, а точка есть 1.

Из всего сказанного напрашивается вывод, что ограниченные нечетные числа пригодны для определения «постоянного» и «знаний», в то время как неограниченные четные числа могут выражать себя только через «непостоянное мнение». В подробности доказательства лучше не вдаваться.

Далеко не все в нумерологии «ограниченного» столь наивно, как в приведенном примере. Если «все сущее есть число», как утверждал Пифагор, должна быть возможность доказать, что весь космос есть число. Пифагорейцы довели это доказательство до конца в наиболее гениальной форме применения своей теории ограниченного. Их решение проблемы пространства стало ранней попыткой дать последовательный разбор размерности. Что означают слова: конкретное пространство имеет один размер, или два, или три? Удовлетворительный ответ, пригодный для любого пространства (ограниченного или безграничного) числа размерностей, был найден только в 1920-х годах. Хотя пифагорейское решение проблемы пространства давным-давно исчезло из разумного восприятия математиков, Пифагор и его ученики заслуживают признания за то, что занялись этой гениальной проблемой. Не искажая значения слова слишком вольно, беспристрастный критик может заявить, что даже при полной ошибочности их решения оно было рационально. То решение оказалось важным шагом для определения четырех материальных элементов с числами и геометрическими фигурами. Перейдем к нумерологическому доказательству, что космос есть число.

Согласно Пифагору, точки есть базовые элементы пространства и только точка имеет место в мире. В отличие от материальных предметов у точки нет ни составных частей, ни магнитуды. Эти недостатки соответствуют числу 1, когда последнее рассматривается как монада или созидательный элемент числа. Если Пифагор думал о пространстве, состоящем из точек, значит, точки создали его космос. Но как бы он ни представлял себе пространство, точку он ассоциировал с числом 1.

Прямая линия, или сокращенно – линия, в нашей геометрии существует вне зависимости от направлений, указанных линией. Но в греческой геометрии линия была просто конечным отрезком нашей линии, и главенствовал постулат, что линия может быть продолжена на любое желаемое (конечное) расстояние. Следовательно, греческая линия имела два конца, каждый из которых был точкой, или числом 1. Итак, в нумерологии Пифагора линия была 2. Становится ясно, почему нечетное число «конечно» или «ограниченно». Например, в 7 = 3 + 1 + 3, где число 1 становится точкой, ограничивающей число 3.

Какое бы определение ни было дано космосу, будет полезно извлечь часть определения из интуитивного представления о протяженности на плоской поверхности. Пифагорейцы определили линию как длину без толщины – возможное обновление определения Фалеса. Таким образом, ни точка 1, ни линия 2 не были «пространством» для пифагорейцев, это попутно означало, что ни 1, ни 2 не получили всех своих привилегий от главенствующих мужских (нечетных) чисел. Но при помощи полностью мужского числа 3 есть возможность достичь реального ограниченного числа, а следовательно, можно надеяться на достижение чистого космоса. Это так, потому что три точки, не располагающиеся на одной линии, необходимы и достаточны для определения любой конкретной плоскости. Действительно, достаточно, чтобы имел место равносторонний треугольник, через который можно провести плоскость, и этот треугольник получается, когда все его три угла соединены между собой. Каждая вершина есть точка, или число 1. Треугольник есть союз трех вершин: 1 + 1 + 1, что равно числу 3. Следовательно, плоскость имеет значение 3.

Предположим, однако, что надо сосчитать сумму не вершин, а сторон равностороннего треугольника. Каждая из сторон есть линия, а следовательно, число 2. Сторон 3, следовательно, треугольник будет равен 3 ? 2, или совершенному числу 6. Но это не так. Ошибка состоит в том, что каждая из сторон была посчитана два раза, потому что две линии сходятся в одной вершине своими концами. Следовательно, необходимо разделить 6 на 2. Результат опять число 3 как число поверхности. Такая проверка на корректность логики должна была доставить Пифагору момент радости.

На следующем этапе появляется новый грандиозный посыл в нумерологии космоса. Линия, о которой идет речь, ограничена, или «предельна», точками. Базовый элемент (точка, 1) всего космоса появился как ограничивающий элемент для вторичного элемента (линии, 2). Это предполагает, что вторичный элемент должен являться ограничивающим или предельным элементом для элемента третьего класса в строении космоса, а именно треугольника. Имеем: треугольник ограничен 3 линиями. Получив на основании замечательного предположения громадной важности закон, применимый к любому пространству, Пифагор в предвкушении демонстрации отважно выдвинул гипотезу, что телесное пространство, пространство материальных тел, есть число 4. Затем, как добросовестный ученый, протестировал свое предсказание на фактах, которые ему казались таковыми. Если бы они подтвердили его правоту, он бы стал самым счастливым человеком на земле.

Простейшим из всех геометрических тел правильной формы является тетраэдр, у которого есть 4 точки, это его вершины, и 4 равносторонних треугольника в качестве граней. Великий принцип ограничения элементами следующего нижнего уровня применим. Но здесь много чего, очень много. Телесное пространство, только что доказанное, есть число 4, являющееся справедливостью по сути, не имеет оснований для сомнений. 4 треугольные субповерхности, ограничивающие и лимитирующие тетраэдр, сами по себе ограничены и лимитированы 6 линиями, являющимися гранями тела, а число 6 совершенно. Более того, 4 грани тетраэдра ограничивают 6 линий, ограничивающие 4 треугольника, ограничивающие тело. Ограниченный подобным образом во всех мыслимых направлениях тетраэдр, и потому еще и телесное пространство, является изначально мужским со своими числами 2, числами 4 и своим совершенным числом 6.

Сущее в данном случае выглядит следующим образом: 1 – точка, 2 – линия, 3 – плоскость, а 4 – тело. Но что-то уже было похожее? 1, 2, 3, 4 есть тетрада, их союз, следовательно, весь космос есть число самой декады: 1 + 2 + 3 + 4 = 10. Поскольку все материальные вещи существуют только в космосе, они тоже есть числа, а тетрады создают их всех. Пифагор был самым счастливым человеком на земле.

Продолжая изучать «все сущее» учителя, в мгновение оказываемся у «категорий», упомянутых Аристотелем в официальном обвинении: «…они сделали вывод на этом основании, что элементы чисел идентичны элементам категорий». Следующей проблемой стала необходимость выделить суть из тетрады 1, 2, 3, 4. Возможно, наиболее привлекательное описание релевантной нумерологии содержится в диалогах Платона. Не придавая значения тому, что сам Платон воспринимал всю эту пифагорейскую физику и химию настолько серьезно, насколько он, возможно, хотел бы убедить нас, нам остается мимоходом отметить, где он все это имел возможность достать.

Около середины V века до н. э. философ Филолай, эрудированный ученик Пифагора, ставший известным около 450 года до н. э., собрал существенный архив поучений учителя. К тому времени братство самораспустилось уже почти полвека тому назад. Как будет видно в следующей главе, распад пифагорейцев как организованного секретного сообщества стал результатом мести Килона. И хотя братство прекратило существовать как активная политическая сила, некоторые из них, кто знавал учителя живым, продолжали топтать землю в интеллектуальных колониях, первоначально основанных материнской организацией в Кротоне. Эти стареющие живые свидетели одной политической чистки, сменявшей другую, оказались в положении схожем с положением интеллектуальных евреев в Европе во времена нацистского режима.

Подозреваемые во всех видах вредительства, к которым они были не причастны, обвиняемые в преступлениях против правящих тиранов, при этом не имея намерения бороться в сложившихся безнадежных обстоятельствах, измученные пифагорейцы прибегали к уловкам, дабы сохранить свои знания, даже если им самим и суждено было погибнуть. Притворная хитрость их счастливых лет стала практической необходимостью, если они не хотели, чтобы учения погибли вместе с братством. Впоследствии всего несколько письменных произведений по пифагорейской науке и философии были найдены, и эти немногие труды передавались из рук в руки под самой торжественной клятвой оберегать секрет. Архив Филолая, как утверждают, стал наиболее полным и наиболее точным среди прочих. Даже в ранние годы Платона, когда активная враждебность к пифагорейской секте осталась в далеком прошлом, пифагорейскую «библию» Филолая было очень трудно достать. Как полагают, Платон достал копию у Архита из Таренто. Архит был восторженным ученым-пифагорейцем. Распознав родственный ум в молодом, но подающем надежды Платоне, Архит великодушно подарил ему бесценную копию пифагорейской «библии». (Один источник говорит, что Платон дал высокую цену за книгу, но по некоторым причинам это звучит неправдоподобно.) За исключением нескольких фрагментов весьма сомнительного авторства, сам труд больше не существует, но письменные упоминания и ссылки на его текст сохранились у греческих историков.

Утрата конспекта Филолая компенсируется бесспорно старательным исследованием, предпринятым со всей глубиной ума Платона, особенно в части нумерологии, представленной, например, в отдельных частях его «Тимея». При отборе для этой книги примеров пифагорейской химии и астрономии много чего было взято из диалогов Платона, к которым любое заинтересованное лицо может обратиться за дальнейшими деталями. Многое, хотя и с критических позиций, дал Аристотель в своих комментариях к науке пифагорейцев. Но по разумной, пользующейся доверием традиции позднейшие греческие историки и философы основывали свои исследования на «библии» Филолая.

Написанный спустя не менее пятидесяти лет после гибели Пифагора, насколько этот конспект заслуживает доверия как первоисточник? Схожий вопрос можно задать в отношении наших Евангелий, ведь, как утверждают некоторые критики, они были записаны не раньше семидесяти или восьмидесяти лет после распятия. В целом, как кажется, мы не сильно собьемся с пути, если отдадим должное Пифагору и его ученикам, как сделал это Платон.

Ссылаясь на труды Платона о науке Пифагора, пренебрегая хронологическим порядком, оказываемся на его месте, когда он сам пришел к этериализации нумерологии Пифагора, чтобы разглядеть ее «неуклонно и в полном объеме», такой, как она есть.

Будет показано, что материальные вещи суть числа. При доказательстве (нумерологическом, конечно), что животные есть числа, приведем пример доисторического искусства. Число любого животного, или любого вида животных, таких как «человек» или «лошадь», определяется унифицированной анатомической арифметикой. Схематичное изображение, скажем человека, нарисовано на песке. У человека, безусловно, есть отличительные признаки: две руки, две ноги, одна голова, одно сердце и т. д. На частях диаграммы поместим гальку, по одной на часть тела. Общее количество булыжников и есть требуемое число. Кстати, это пример подсчета в первоначальном значении слова, поскольку латинское слово calculus, счет, означает «галька».

Недавнее (1942) наблюдение английского натуралиста, сделанное в Индии, свидетельствует о более раннем схематичном представлении о строении человека. Согласно данным указанного обозревателя, начало этого искусства уходит корнями в дочеловеческие времена. Оказывается, еще обезьяны, наводнявшие конкретную индийскую деревню, избрали плоскую вершину холма поблизости для своей культурной деятельности: подвижных игр, ухаживаний и отдыха. Время от времени одна из шаловливых обезьян предпочитала неожиданно прерывать свои танцы, второпях опускаться на корточки, сильно упирать свою левую руку в песок и палочкой, зажатой в правой руке, как карандаш у чертежника, быстро проводила линию вокруг отпечатка левой руки. Затем, очевидно опасаясь, что делает что-то противоестественное, художница вскакивала и убегала на ближайшее дерево. После чего остальные обезьяны собирались вокруг творения, рассматривая его с трепетным восхищением. Это настоящая рука или это абстрактное изображение всех рук, универсальная Рука в сфере Божественных помыслов? Подобно нам, они не могли постичь увиденное. Они возвращались к своим обыденным занятиям.

Посередине между камнесчетом живых существ и более серьезной полугеометрической нумерологией четырех элементов расположена еще одна система счета Пифагора, значительная часть которой вошла в немистическую высшую арифметику наших дней. Она нашла отражение в истории о купце, которого Пифагор спросил, умеет ли тот считать. Получив утвердительный ответ, Пифагор попросил продолжить.

– Один, два, три, четыре… – начал купец. Тут Пифагор закричал: – Стоп! То, что вы называете четыре, на самом деле то, что вам следует назвать десять. Четвертое по порядку число не четыре, а декада, наш тетраксис и священная клятва, которой мы клянемся.

Чтобы удовлетворить Пифагора, купцу пришлось считать (в наших цифрах) 1, 3, 6, 10, 15, 21, 28, 36… Это так называемые треугольные числа; когда их представляют в виде гальки, они образуют равносторонние треугольники. Пифагор располагал эти числа следующим образом:

и далее в том же роде.

Следующие, 15, формируются выкладыванием вдоль 10-го треугольника, вдоль любой из его сторон, дополнительной гальки в количестве 5 штук, следующее число 21 соответственно добавлением 6 камешков, за ним добавляют 7, потом 8, далее 9 и т. д.

Квадраты целого числа – те же камешки гальки, выложенные по тем же правилам, где 9 получается из 4 выкладыванием камешков вдоль двух прилежащих сторон 4, а 16 выкладыванием вдоль 9. Следующее число 25 получается из 16 и так далее до бесконечности. Таким же образом – любая другая прямоугольная фигура на плоскости (все стороны равны, и все углы равны) устанавливает рамки для выкладывания гальки по классам так называемых многоугольных чисел: пятиугольное число, шестиугольное число, семиугольное число, восьмиугольное число и так далее насколько пожелаете.

Эта связь между правильными геометрическими фигурами и соответствующими последовательными рядами чисел имела важное значение для пифагорейцев, а после них для платонистов, отчасти из-за очевидного единения космической симметрии с числами, а отчасти из-за тетрад и декад, проявлявшихся неожиданно в различных обликах. Были и так называемые продолговатые числа, соответствующие камешкам гальки, разложенным в виде прямоугольника со стороной отличной от предыдущей на 1 камешек, например: 30 = 5 ? 6. Когда Пифагор обратил внимание на то, что продолговатое число равно двойному треугольному числу, как в случае с 30 = 2 ? 15, он испытал безграничный душевный подъем.

Ободренный видимым успехом с плоскими фигурами, Пифагор отважно ввязался в рискованное предприятие с геометрическими телами. В воображаемом пространстве он успешно выложил из гальки кубические числа 1, 8, 27, 64, 125… унифицированным способом, который может быть оставлен гениальному читателю, желающему открыть его вновь. И тут он застрял, потому что космос для него, как и для всех остальных греческих нумерологов и геометров, имел только три измерения. Они могли себе представить результат умножения трех чисел как объем твердого тела. Так, 3 ? 4 ? 10 = 120 есть объем короба со сторонами 3, 4, 10. Но умножение типа 3 ? 4 ? 10 ? 12 сбивало их с толку в их геометрической арифметике, поскольку выражение «умножить четыре линии» лишало само действие смысла в трехмерном пространстве. Подобные искусственные барьеры просто исчезли, когда алгебра заняла место геометрии в качестве языка чисел. Но треугольные и прочие многоугольные числа пифагорейцев, а также кубические выжили, по меньшей мере как названия в современной теории чисел. Продолговатые числа исчезли из словаря давным-давно.

Наиболее значимой деталью для всей пифагорейской науки было четвертое из треугольных чисел 1, 3, 6, 10, 15, 21… Да, 10 или декада. Но при этом и треугольник, а потому – священный тетрасис. Поскольку, согласно Пифагору, все числа находятся внутри декад, становится ясно, почему десять было совершенством для остальных чисел и, согласно Платону, исконным образцом для вселенной. Становится понятен и краеугольный камень обобщений Платона, что мир создан из треугольников. Это будет подтверждено, когда 4 элемента произойдут от 4-го члена последовательности треугольных чисел, конкретно из треугольных декад. Неудивительно, что братство пифагорейцев превратило 10, действительно 4-й треугольник, в свою клятву и свой наиболее жестко охраняемый секрет. Тот, кто дал клятву на тетрасисе и нарушил ее, предавался анафеме, поскольку он предал космос, частью которого был сам, греки бы сказали пропорцией или дробью.

Хотя может показаться занимательным распутывать всю замысловатую нумерологию (в изложении Платона, в частности в «Тимее») создания и структуры материального мира, но нет необходимости это делать, чтобы понять суть идеи пифагорейской химии, физики и космогонии. Вполне вероятно, окажется достаточно уже представленных материалов, чтобы оценить ее возможности в столь типичном отрывке: «Итак, то, что было создано, обязательно телесно, а также видимо и осязаемо. Ничего не видно там, где нет огня, и осязаемое не телесно без земли. По этой причине божественное в начале создания сотворило тело мироздания из огня и земли. Но две вещи не могут существовать без третьей, у них должно быть связующее звено. Ныне прекрасная связь – это та, которая наиболее полно объединяет связанные вещи. Пропорции хорошо подобраны для поддержания этой связи. Всякий раз среди трех чисел, какой бы телесной или иной другой она ни оказалась, не имеет значения, потому что среднее значение есть последнее условие, поскольку на первом плане – среднее значение, а когда значение есть наипервейшее условие, то и последнее условие приобретает среднее значение, и оно становится и первым, и последним, а первое и последнее становятся значимыми, все вещи по необходимости приходят к одному знаменателю, поскольку они едины и стремятся слиться воедино».

Нет сомнений, что это список с утерянной «библии» Пифагора от Филолая, поскольку это чистейший пифагореизм. Чтобы понять, о чем идет речь, следует воспользоваться помощью перевода с запутанного языка на более простой эквивалент в терминах простейшей арифметики. В действительности отрывок относится к банальным конкретным свойствам банальных дробей. До некоторой степени запутанная арифметика нам понятна. Но она была совсем не так понятна пифагорейцам V века до н. э. или даже греческим математикам времен Платона, никто из которых не владел умением толково записывать дроби. Смешно, но для гимназиста XVIII века этот невразумительный отрывок яснее, чем для выпускника колледжа наших дней.

За исключением старомодных учебников, редко встретишь «соотношения» и «пропорции» в современных научных трудах. «Соотношение» числа m к числу n записывается как m/n или 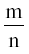. Если соотношение m: n равно соотношению r: s, в античные времена записали бы m:: n:: r: s; а в наши дни  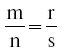или m/n = r/s. Даже использование старой манеры записи понять много легче, чем то, что использовали пифагорейцы и их греческие последователи. Они не имели столь выразительных математических символов, как у нас, а все описывали словами, как в предыдущем отрывке у Платона. «Существенными деталями являются «пропорция» и «среднее значение».

Четыре числа, скажем m, n, r, s, связаны «пропорцией», где первое соотносится со вторым, как третье с четвертым, или на языке дробей, где дробь m: n равна дроби r: s. Следовательно, m, n, r, s состоят «в отношении», если m: n:: r: s в нашем простом примере, 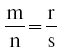, есть «условия» «пропорции».

Возникает множество специальных случаев. Такие, как средние значения n, r, равны и, следовательно, r = n и m: n:: n: s, которые были очень важны для пифагорейцев, а также для греческих геометров. В этом случае n именовалось «средним геометрическим значением» между экстремальными точками n, s «среднего пропорционального значения» для n, s. Переводя все на понятный язык дробей, имеем 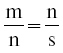, и, таким образом, как известно ученику начальной школы («освобождаемся от дробей»), m ? s = n ? n, в элементарной алгебре ms = n².

Следовательно, «среднее геометрическое значение» (n) двух чисел (m, s) есть корень квадратный (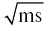) от их результата (ms). Арифметика в тексте Платона означала именно это. Из «пропорции»  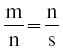незамедлительно следует, что  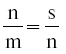(если обе дроби равны, результатом деления будет 1, поскольку каждая из них также равна). Это как раз то, что он говорит: m: n:: n: s, – из чего следует, что n: m:: s: n, где «среднее значение» n в первоначальной «пропорции» становится как первым, так и последним вторым числом, а первое и последнее m, s в первоначальной пропорции становятся «средними значениями» в «пропорции», вытекающей из первоначальной. Таким образом, элементарная арифметика у Платона в порядке.

Чтобы разобраться в других замаскированных арифметических расчетах философии Платона, надо вспомнить следующие дефиниции.

В последовательности чисел

1, 5, 9, 13, 17, 21

шаг между числами остается прежним – 4. Числа формируют «арифметическую прогрессию» с первым членом 1 и «разностью арифметической прогрессии» 4. Арифметическая прогрессия с начальным членом 6 и разностью 5 следующая:

6, 11, 16, 21, 26, 31…

Бросается в глаза, что 16 = ¹/₂ (11 + 21), 21 = ¹/₂ (16 + 26) и так далее, где каждое последующее число после первого есть половина суммы от своих правого и левого соседей. По этой причине каждое число после первого называется «средним арифметическим значением» непосредственно предшествующего числа и непосредственно последующего.

Теперь, допустим, мы делим 1 на каждое число в данной арифметической прогрессии, скажем второй сверху:

¹/6, ¹/₁₁, ¹/₁₆, ¹/₂₁, ¹/₂₆, ¹/₃₁…

Полученная последовательность чисел называется «гармонической прогрессией», где каждое число после первого является «гармоническим средним значением» своих непосредственных соседей. В качестве примера одна из последовательностей

³/4, 1, ⁵/₄, ³/₂, ⁷/₄, 2, ⁹/₄…

⁴/3, 1, ⁴/₅, ²/₃, ⁴/₇, ¹/₂, ⁴/₉…

арифметическая прогрессия, а вторая – «гармоническая прогрессия».

Третьим и последним видом прогрессии, постоянно упоминающимся Платоном, является «геометрическая», в которой каждое число после первого получается путем умножения предыдущего числа на постоянный множитель. Например:

3, 6, 12, 24, 48, 96, 192…

является геометрической прогрессией с первым числом 3 и множителем, или общим коэффициентом, 2. «Среднее геометрическое значение» 6 и 24 есть число 12, расположенное между ними, среднее геометрическое значение 48 и 192 есть 96 и т. д.

Несложные алгебраические преобразования продемонстрируют, что если A, H, G соответственно арифметическое, «гармоническое» и геометрическое средние значения чисел M, N, тогда

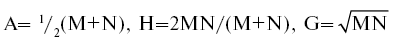
Еще чуть-чуть, и становится очевиден простой факт, который обрадовал и ввел в заблуждение древних нумерологов, включая Платона, ведь получается, что G есть среднее геометрическое значение для A and H. В целом, похоже, греческим философам повезло, что они не знали алгебры. Теперь вся элементарная и замаскированная алгебра Платона стала настолько банальной для современных школьников, что любой математик обязан восхититься упрямой изобретательностью, которая впервые задумалась над этим пусть и устно, без математических символов любого рода. Выражение, что A/G = G/H, или A: G:: G: H, было названо пифагорейцами «совершенной пропорцией». Говорят, что его принес Пифагор в Кротон из Вавилона. Любой математик с достаточно развитым воображением в состоянии лишить себя на мгновение всей накопленной техники и задуматься над риторической арифметикой VI века до н. э. и согласиться с братством пифагорейцев, что «совершенная пропорция» не могла быть изобретением человека, а только творением лично Великого арифметика вселенной.

«Гармоническая прогрессия» и среднее «гармоническое значение», не выраженное явно в важном открытии, является результатом нумерологического выражения закона музыкальных интервалов, который вдохновил Пифагора на его изречение «Все сущее есть число». Он и его ученики искали музыку и гармонию в четырех элементах всех материальных вещей и небесных тел. То, что они нашли искомое, не столь удивительно, когда мы вспомним, что вся гармония, весь космос, все предметы и все тела, небесные и земные, вписаны в декады, которые в основе всего. После того как Платон изложил теорию, продолжив по окончании доказательства, что все есть единица, а следовательно – божество: «Если теперь рамки вселенной были созданы просто как поверхность без глубины, единица приобрела значение достаточное, чтобы объединить ее с другими условиями. Но поскольку мир должен быть тверд, а твердые тела всегда плотные, и не по одной причине, а по двум, бог дал воду и воздух как среднее значение между огнем и землей и, насколько это возможно, заставил их придерживаться пропорции, поскольку огонь нужен воздуху, воздух нужен воде, а если воздух нужен воде, то вода нужна земле. Так он создал и объединил видимые и осязаемые небеса. Вне четырех элементов он расположил тела во Вселенной в совершенной гармонии и пропорции (совершенной пропорции). Будучи, таким образом, наделенным духом дружбы, в полном единении с самим собой, космос стал неразрушимым для любой другой руки, кроме руки творца».

Не вдаваясь в детали этого конкретного утверждения об основных принципах, отметим, что «дух дружбы» относится к любопытным особенностям конкретных пар чисел, открытых пифагорейцами. Если каждое из чисел m, n равно сумме делителей эфира, то т, п называются «дружественной парой чисел», а m, n становятся «дружескими», или «дружественными», числами. Что касается делителей «совершенных чисел», само число не рассматривается как делитель. Наименьшие «дружественные числа» – это 220 и 284. Пифагорейцы рассматривали этот близкий союз между «дружественными числами» как концентрированное выражение дружбы и глубоко спрятанную душу гармонии.

Платон подвел итог своему рассказу о создании мироздания абсолютно нумерологическим отрывком, в котором показал, что бог одарил мир любовью к универсальному Животному, «содержащему в себе всех других животных». Доказательство, что это Мировое Животное не знает смерти и разложения, как у других животных, включая человека в его бренном теле, было невразумительно даже для нумерологии. Цитируемая часть, однако, представляет глубокий научный интерес, при этом науку следует понимать в духе пифагорейцев. Двух-трех комментариев хватит для ясного понимания. Следующий текст – просто краткий курс пифагорейской космогонии и космологии.

Правильное твердое тело – это тело, стороны которого составляют правильные многоугольники, одинаковые по размеру и форме. Если быть точным, пять правильных тел возможны и могут быть построены в нашем трехмерном пространстве (Евклида). Первое – это тетраэдр, у которого четыре равносторонних треугольника составляют стороны, второе – куб, или шестигранник, у которого шесть квадратов составляют стороны, третье – восьмигранник, где восемь равносторонних треугольников составляют стороны, четвертое – двенадцатигранник, у которого двенадцать правильных пятиугольников составляют стороны, и пятое – это двадцатигранник, у которого двадцать равносторонних треугольников составляют стороны. Четырехгранник, шестигранник, восьмигранник, двадцатигранник, но не двенадцатигранник были известны Пифагору. И когда ранние пифагорейцы ошибочно предположили, что возможно создание и существование только четырех правильных тел (очень скоро Платон докажет существование пяти), это вдохновило их на доказательство, что все четыре соответствуют четырем базовым элементам материальных тел.

В качестве умозрительного предположения, которое они приложили к своей космической нумерологии, они представили свой постулат, что четыре элемента: огонь, воздух, земля и вода – соответственно есть четырехгранник, восьмигранник, шестигранник (или куб) и двадцатигранник. Гранями у всех фигур, кроме шестигранника, являются треугольники. Этот недостаток был легко преодолен путем деления каждой грани куба на два треугольника простым проведением диагонали по площади. Таким образом, как отмечает Платон в «Тимее», речь теперь шла только о треугольниках. Числа, соответствующие треугольникам, олицетворявшим элементы, стали 4, 8, 12, 20. Затем эти числа, коль нумерология настаивала на том, могли быть использованы как числа, которые «олицетворяли» элементы: огонь, воздух, землю и воду – соответственно.

«Неотъемлемая треугольность» материи невольно идентифицировалась с магическим числом 3, наводила на мысль, что 4, 8, 12, 20 будут соответствовать высшему достоинству в нумерологии химии Пифагора. Но не исключались и другие возможности, поскольку допускалось, что результирующие числа способны каким-то образом быть прилажены к четырем базовым элементам, известным пифагорейцам, когда они в некоторой степени в предварительном порядке объявили о своей теории элементов. Позволяя себе разумную свободу, можно легко проверить нумерологию Платона, согласно которой «бог создал воду и воздух как средние значения между огнем и землей».

Но если цель состоит в том, чтобы доказать базовую теорему, что все значимое есть треугольник, можно это сделать более элегантно и более удобно (для хорошего нумеролога) посредством следующих 6 пропорций, где F, A, E, W являются соответственно огнем (четырехугольник, 4), воздухом (восьмигранник, 8), землей (шестигранник, 12), водой (двадцатигранник, 20)

F: A:: 3: 6, A: E:: 10: 15,

F: E:: 1: 3, A: W:: 6: 15,

F: W:: 3: 15, E: W:: 6: 10.

Числа, появившиеся в этих мистических пропорциях, следующие: 1, 3, 6, 10, 15. Но это же первые пять треугольных чисел, которые сами по себе треугольники. Поскольку существует точно 5 правильных тел и точно 6 необходимых пропорций продемонстрированного вида и поскольку 6 были представлены, то следует, что допущение справедливо, как объявил Платон, потому что число 6 совершенно. Этим заканчивается доказательство, которое само по себе совершенно, так как состоит из 6 пропорций. Насколько известно, это красивое доказательство не пришло в голову пифагорейцам и их последователям.

Теперь задумаемся, что могло заставить пифагорейцев прежде всего заняться идентификацией четырех элементов Эмпедокла с четырьмя правильными фигурами, известными им? Существует множество ответов, еще больше ответов можно себе представить. К сожалению, оставив без внимания древние ответы на эту знаменитую головоломку, процитируем одного мудреца-астронома, математика и нумеролога много более поздних времен. Йоган Кеплер, живший в 1571–1630 годах, ставший бессмертным астрономом за три закона движения планет по своим орбитам. Опираясь на законы Кеплера (вполне успешно), Ньютон открыл свой закон всемирного тяготения. Последствие слишком известно, чтобы его пересказывать в данной работе. Но интересный факт: всего семьдесят лет разделяют законы Кеплера и законы Ньютона. Первый из идолов науки был явным нумерологом, в то время как второй, построивший свое достижение на надежном основании, заложенном первым, сообразно складу ума и характера был не способен признать хоть что-либо из нумерологии. В этом плане нумерология и теология схожи: незаурядные человеческие способности проявляются независимо от того, верит или не верит он, верит в одно или в другое. Некоторые из ведущих научных нумерологов XX века известны в науке не меньше своих оппонентов, которые презирали всякое проявление мистики чисел.

Решение проблемы элементов у Кеплера было гениальным и обворожительным. Среди всех правильных фигур четырехугольник имеет наименьшую величину площади поверхности, в то время как двадцатигранник наибольшую. Но этот показатель величины площади был разновидностью показателей сухости и влажности соответственно. Поскольку огонь – самый сухой из четырех элементов, а вода – самый мокрый, тогда четырехугольник – это символ огня, а двадцатиугольник – символ воды. Чтобы облегчить восприятие, Кеплер украсил рисунок четырехугольника изображением костра, а двадцатиугольника – раком с абстрактной рыбой. Очевидно, согласно Кеплеру, земля – это куб. Если, с позволения сказать, любой материальный предмет на планете Земля может расположиться более уверенно на четырехугольном основании, чем куб, даже Бог не ведает, что бы это могло быть. Кеплер украсил свой земной куб морковкой, деревом и различными садовыми растениями. Нумерологически и физически противоположностью сверх-устойчивому кубу является неустойчивый восьмигранник. Если это тело слегка придерживать за две противоположные вершины указательным пальцем и большим пальцем руки и щелкнуть его, он начнет вращаться, как волчок. Это обращение к опыту призвано доказать, что восьмигранник нестабилен, как воздух. Профессиональные знания подтвердили – это воздух. Это материальное тело было разрисовано облаками и летающими птицами. Последним оказался двенадцатигранник – крепостной химии Пифагора, со своими двенадцатью пятиконечными гранями. Он не мог стать одним из четырех элементов, поскольку они были уже приписаны к многогранникам. Чем же, черт возьми, его можно представить? Явно нечем. Он должен стать, как осознал Платон задолго до Кеплера, «небесным объектом». Но знаки зодиака символизируют чистые небеса. Поскольку знаков зодиака двенадцать, а у додекаэдра двенадцать граней, пусть двенадцатигранник символизирует вселенную. Графическое изображение тела было украшено изображениями солнца, луны и звезд.

Небесный додекаэдр был величайшей головной болью для пифагорейцев, как и проявление дисгармонии с квадратным корнем из двух, которое не является рациональным числом. Их доказательство, что элементов всего четыре и они правильные тела, было практически завершено, когда появился пятый правильный элемент – двенадцатигранник. Он оказался наименее желанным. Гипас, один из членов братства, как говорят, представил новое тело своим коллегам, принявшим новость достаточно холодно. Одна из легенд утверждает, что Гипас был брошен в лодку без парусов, весел и руля, дабы наказать за его самонадеянное утверждение, что это страшное открытие совершил он сам, а не учитель. Другая легенда гласит, что Пифагор

был настолько смущен появлением двенадцатигранника, что приказал убить первооткрывателя, тело которого зашили в мешок и сбросили в море на скалы. (Вся хронология в легендах искажена.) Но двенадцатиугольник нельзя было спрятать, и братство приняло меры, чтобы извлечь из ситуации максимальную выгоду. Чтобы объяснить, как, к своей радости, они додумались, что он все же встраивается в их нумерологию вселенной настолько удачно, насколько ключ подходит к замку, следует проанализировать знаменитый труд Платона «Брачное число». Но он слишком запутан и усложнен загадками, чтобы вскользь разбираться в нем. Достаточно сказать, что двенадцатиугольник, вместо разрушения нумерологии четырех элементов Пифагора, блестяще подтвердил ее в мелочах и раскрыл гармонию, о которой даже не догадывались, Гармонию необыкновенной красоты в имеющихся в изобилии тетрадах, огромных тетрасисах и все созидающих монадах.

Упоминание Платона о неудобном двенадцатиугольнике так поэтично, как и его «толкование» четырех «элементных» тел. «Пятое тело, – пишет он, – было использовано, чтобы украсить небеса с плеядами». Додекаэдр поэтому не стал элементом сущего, а только неуловимым «воплощением», «пятой сущностью» всех элементов и сутью вселенной. За дальнейшими деталями следует еще раз обратиться к «Тимею».

Чтобы вернуться на момент на Землю прежде, чем покинуть элементы навсегда, запомним деталь доказательства пифагорейцев, что земля есть куб, что, кстати, вошло в нашу повседневную речь. Земля есть «квадрат». Почему? Потому что у нее четыре кардинальные точки, и линия, соединяющая север и юг, пересекает линию, соединяющую восток и запад под прямым углом, опять квадратный феномен, и поэтому справедливо, поскольку 4 есть божественная справедливость Единицы.

Покидая Землю и все ее элементы, последуем за Пифагором в более высокие сферы небесных тел, чтобы приобщиться вместе с ним к части той небесной гармонии «музыки сфер», которая подбадривала Кеплера в самые мрачные часы бедности, домашней трагедии, травли и двадцати одного года подавления, когда он считал, считал, считал, чтобы открыть законы планетарных орбит. Только пифагорейская уверенность в гармонии чисел во вселенной поддерживала его в перемалывании монотонной работы и подгоняла от одного разочарования к другому, пока наконец он не превзошел свои самые амбициозные надежды. Если нумерология доставляла удовольствие Кеплеру, ее стоит простить за любые шалости, что она с ним себе позволяла, пользуясь его упрямым легковерием.

Увидев раз, как закон музыкальных интервалов вдохновил Пифагора на философию чисел, следует посмотреть его глазами на полученную в результате музыку божественных декад. К своей радости по этому поводу, Пифагор открыл, что тетрады 1, 2, 3, 4 как таковые содержат небесную гармонию. Что до «октав» в нотах, то справедливо соотношение ²/₁ с их «пятой» в соотношении ³/₂ и с их «четвертой» в соотношении ⁴/₃. Эти базовые, установленные опытным путем факты гармонии были открыты (возможно) передвижением клина монохорда и подергиванием различных долей струн.

Пифагорейцы, а после них Платон вывели из элементарной акустики: вселенная одушевленная и небеса с планетами и «зафиксированными» на сфере звездами есть число и гармония. Одной детали доказательства вполне достаточно для примера. Поскольку в музыкальной гамме Пифагора семь интервалов и поскольку на момент изобретения гаммы было известно всего пять подлинных планет, и потому что эти пять планет, если прибавить к ним Солнце и Луну, становятся числом семь, то, следовательно, планеты есть музыкальная гамма. Принимая во внимание фундаментальные постулаты учителя, что все сущее заключено в декадах и что «все сущее есть число», ни один логик или математик не стал бы спорить с доказательством Пифагора или Платона, если только он не имел намерения транспонировать их в символы, с которыми только он был знаком. Такого рода опыт убедит любого, что результат, достигнутый прямым математическим (или дедуктивным) доказательством, может не иметь отношения к миру научного или чувственного опыта или просто не отвечать здравому смыслу. Если постулаты не согласуются с проверяемым или уже проверенным опытом, выводы, основанные на них, не имеют значения в чувственном мире. Подобные утверждения, вне всякого сомнения, банальны, но от этого они не менее справедливы. Любой человек с рациональным мышлением принял бы их, однако многие рациональные ученые убеждали коллег принять фактически непроверяемые утверждения, потому что они были выведены с помощью безупречной логики, математической или иной, из допущений, которые рациональному мышлению нет нужды принимать.

Итак, нам придется опять воздержаться от презрительной усмешки в адрес науки и теологии наших предшественников.

Принимая сказанное во внимание, было бы крайне поучительно взглянуть на выводы, которые ученые мужи, чей интеллект был явно не ниже нашего, вывели из кругового движения планет. Начнем с Платона и его выводов, наиболее рафинированных из всех.

«Когда разум, – начинает Платон, – который занимается равными истинами как в круге Иного, так и в круге Такого же, в сфере самодвижущегося безмолвного движения тишины, когда разум, говорю я, находится вблизи восприятия, а круг Иного также движется по намекам разума для всей души, тогда появляются справедливые мнения и убеждения. Но когда разум попадает в зону рационального и круг Такого же, плавно продвигаясь, свидетельствует об этом, тогда образование и знания неизбежно совершенны». Все подобные утверждения поддаются прямому доказательству при допущении, что мы принимаем постулаты нумерологии пифагорейцев. Но все они потеряли ту значимость, которую когда-то могли иметь, возможно кроме чрезвычайно зачаточного описания движения планет. Тем не менее не все из подчеркнутых высказываний, сокрытых в совокупности мысленных образов Платона о сферах и движущихся кругах, утратили свое значение, когда мысль человеческая расширилась «солнечными процессами». Было бы интересно увидеть, какими могли бы быть некоторые предполагаемые факты в сокрытой астрономии метафизики Платона о «чувстве» и «разуме». Пифагорейцы отталкивались от наблюдения (возможно, теневых контуров во время затмения), что Земля есть сфера или как минимум закругленная. И это был предполагаемый факт, такой же старый, как само человечество, что звезды закреплены на поверхности широкой сферы с Землей в центре. В данном случае слово «чувство» (чувственный опыт), о котором говорил Платон, запутал разум. Никакой сферы нет, хотя чувственное, зрительное восприятие подтверждает это с такой же уверенностью, с какой астрономы, раздвинувшие человеческое видение с помощью созданных человеком инструментов, сообщают, что нет пределов по глубине «звездных небес». Тверже, чем сам Пифагор в своей вере в число, Платон пренебрег наблюдением в астрономии и вывел шарообразность Земли напрямую из допущения, что из всех тел совершенна только сфера. И подобным же образом он поступил с небесной сферой для звезд. Они обе должны быть сферами, что вытекает из того, что Единица, создатель небес и Земли, самим своим совершенством не может создать ничего несовершенного.

Пифагорейцы были не столь категоричны, как Платон, в пренебрежении индуктивным методом, основанным на чувственном восприятии. В центр своего космоса они поместили Гестию и ее Центральный огонь, чтобы распределить пламя и тепло на Солнце и другие планеты. Теперь это кажется достаточно наивным предположением. Но необходимо помнить, что надо было как-то пристраивать богов, а Гестия предложила именно то, что требовалось. Невидимый глазам простых смертных, Центральный огонь стал объектом размышлений бессмертных, видевших все, при этом оставаясь незамеченными. Отец богов и людей, следовательно, использовал Гестию как хранительницу смотровой башни, с которой можно было обозревать грешное человечество.

Хотя Гестия не была солнцем, как это могло поспешно показаться, этот гипотетический центральный очаг вселенной дал Копернику, жившему в 1473–1543 годах, толчок к его гелиоцентрической теории строения Солнечной системы. По крайней мере, он (или его любезный редактор) написал об этом в посвятительном послании тогдашнему папе римскому, возможно в попытке избежать порицания, подкрепив описание своего нововведения ссылками на Античность. Так Гестия, хотя и чистая выдумка, и слабая гипотеза, наконец оправдала Пифагора на суде науки.

Вокруг невидимого очага своей вселенной пифагорейцы расположили Землю, Луну, Солнце, пять планет, известных в то время, и сферу с неподвижными звездами. В наборе не хватало десятого элемента, как требовала совершенная десятерица. Мы уже не раз показывали, как они покрывали дефицит, подставив невидимую планету Антипод между Гестией и Землей. Это десятое тело их небесной системы было более реально для них, чем девять остальных, поскольку это было абстрактное число десять.

Скептик, не веривший в богов, едва ли мог согласиться с теологическим объяснением невидимости Центрального огня. Чтобы удовлетворить и его, пифагорейцы измыслили одну из своих наиболее оригинальных теорий. Населенные регионы Земли, указывали они, все расположены на той стороне Земли, которая всегда повернута в противоположную сторону от центра ее орбиты. Поэтому, чтобы увидеть Центральный огонь, было бы необходимо пройти дальше Индии. Поскольку даже сам Пифагор не путешествовал так далеко, маловероятно, что кто-то еще сделает это. Но предположим, такой человек нашелся. Гестия все равно останется ему не видна, потому что между ней и Землей окажется невидимый Антипод. Разве путешественник не может подождать, пока Анти-Земля пройдет мимо? Он не может: Земля и Анти-Земля держат равную скорость, вращаясь вокруг Центрального огня. Даже новаторы XIX века, заполняя космическое пространство, не могли объяснить невозможность увидеть невидимое.

Заполнив небесную декаду с нумерологической точки зрения, каждое из десяти небесных тел распределили на свою собственную вращающуюся сферу. Расстояния этих вечно вращающихся сфер от Центрального огня предположительно соответствуют простым нумерологическим отношениям одного числа к другому. Естественно, тетрады и их гармоничные отношения были открыты в этой небесной арифметике. Они были ловко внедрены в нее до начала астрономических вычислений. Декады были также спрятаны в десяти небесных телах, сферы в своем движении создавали к тому же неслышимую музыку, «музыку сфер», которая очаровывала ученых и поэтов от Пифагора и Платона до Кеплера и Шекспира: «Нет, то не круг, что у тебя в руках, / Он как полет божественных созданий, / Еще поет как хор церковный в храме» – так говорил Лоренцо Джессике. Абсурд, без сомнения, но в какой-то степени угнетает меньше, чем морской альманах. Венценосная каверзность всего этого состояла в совершенно рациональном объяснении, почему же так случилось, что смертные (за редким исключением в лице настырного и одаренного богатым воображением Кеплера) не слышали ничего о небесной гармонии сфер. Это возвращает нас обратно во времена Пифагора и легендарной наковальне. Потому что наковальня продолжает издавать свой резкий металлический звук вечно, днем и ночью, год за годом, музыка сфер производит на наш истощенный слух не больше впечатления, чем грохот в кузнице с десятью музыкальными наковальнями. Этот штрих наверняка добавил сам учитель.

Возможно от более прямой интеллектуальной честности, чем у Пифагора, Кеплер с презрением относился к попыткам уклониться от настоящих трудностей при помощи таких слишком поверхностных ухищрений. Уверенный в том, что его неземная душа, если не все буйные чувства, ощущает небесную гармонию, Кеплер записал песню сфер на нотный лист. Медлительные тела, оказавшись рядом с Центральным огнем, поют басом или контральто, как и у Пифагора, издалека, но высоким голосом поет тенор или сопрано. Мелодия едва ли сравнима по сложности с любой из необычных симфоний планет Холста. Но она устраивала Кеплера, когда он выстукивал ее для себя, делая расчеты одной за другой орбиты, плохо сочетающейся с другими орбитами, в самой удивительной работе по арифметике, когда-либо выполнявшейся подверженным ошибкам человеком для получения проверяемого научного результата. Музыка, услышанная Кеплером, должна была быть чище и проще, чем мелодии сирен, что транспонировал Платон в свою небесную метафизику.

Переходя сейчас к более высокой области пифагорейской астрономии, необходимо вернуться к далекой предыстории, задолго до того, как Египет и Вавилония были лишь предполагаемой возможностью для кочевых племен, совершавших свои переходы в местах будущих центров древних цивилизаций. В умеренном климате до сих пор не обнаружено каких-нибудь апатичных к знаниям рас, которые не обращали бы внимания на неизменное повторение весны, лета, осени и зимы. Века пассивного наблюдения особенностей поведения небес, например смены времен года, научили первобытных людей, что смена времен года и движение созвездий настолько предсказуемы, насколько предсказуема смена дня и ночи. Медленно раздвигая границы познания в астрономии, они установили более замысловатые периодичности в движении небесных тел и менее заметной смене сезонов и спустя тысячелетия добрались до наивысшего уровня в потрясающем открытии о предварении равноденствий. Следом зафиксировали на небесах Великий год (то есть полный цикл предварения равноденствий), равняющийся около 25 800 годам, в конце которого все движение начнется вновь по старым марш рутам, которые они только что завершили, пока новый Великий год не начнет свой путь по небесам, и тогда цикл повторится еще раз, и так далее, пока существуют звезды. Повторение этого вечного движения имеет точность до минуты: это не просто последовательность созидания, как представлял себе Анаксимандр.

Одно из наиболее понятных и побуждающих к мысли утверждений в данной циклической теории движения вселенной, хотя и долго непризнаваемое, разумеется, принадлежит Евдему Родосскому, неизвестно когда родившемуся, но жившему до 350 года до н. э., ученику Аристотеля, историку математики и астрономии. Его версия, по крайней мере, намекает на видение Платоном Великого года, или Вечного движения. Евдем, обращаясь к своим ученикам, говорит: «Если верить пифагорейцам, то наступит час, и я снова буду секретничать тут с вами, и в руке у меня будет такая же маленькая указка, и снова вы будете сидеть передо мной, и так будет со всем остальным». Время и вечность идут по жизни в паре, как на изображении змеи Уроборос, пожирателя своего хвоста, пожирателя, не покусившегося на «бессмертного червя». Этот мрачный сон вращения времени, как говорят, посещал вавилонян, когда они открыли предварение равноденствий. До тех пор Время не настолько было захвачено Вечностью, и оставалась надежда, что человек может стать хозяином своего будущего. Но когда стало очевидным, что небесные тела повторяют все сложные элементы своего пути бесконечное число раз, стало ясно, что Время, почти поглощенное Бесконечностью, мгновенно объединило прошлое и настоящее. На основании этого открытия все, что случилось когда-то, начинает случаться заново, поскольку оно должно происходить время от времени, раз уж Время и Вечность впервые объединились.

Должно существовать что-то непреодолимо привлекательное для пытливого ума в этом древнем изображении змея, ловящего себя за хвост. Любопытная деталь его собственного кольцевого движения в созерцательной философии от вавилонян до Ницше, жившего в 1844–1900 годах, состоит в том, что многие из веривших в круговое движение Времени также поверили в то, что они были первыми, кто когда-либо поверил в бесконечно повторяющееся движение вселенной. То, что здесь содержится очевидное положение, противоречащее самому себе, вовсе ничего не значит для тех, кто, подобно несчастному Ницше, самоистязал себя, безумно размышляя об ужасе бесконечной реинкарнации в их теперешнюю форму. Лучшим примером бездумной отваги неконтролируемого воображения при экстраполяции одного обозреваемого факта (в данном случае предварения равноденствий) на другой является Вечное движение.

Было бы интересно рассмотреть нумерологическую версию Платона о Вечном движении, особенно в беспорядочном сплетении его Великого года с Брачным числом, затянутым в крепкий узел, но следует двигаться дальше, кратко остановившись на одном или двух витках. Брачное число, как утверждает ряд экспертов по платонизму, равно 60 в четвертой степени, или 12 960 000. Это большое число было упомянуто в связи с арифметикой вавилонян, там же было отмечено, что одним из самых жестких требований к осмысленному вниманию всех нумерологов является наличие множества делителей. Мистические последствия этого факта элементарной арифметики неисчерпаемы.

Чтобы найти подсказку и определиться с возможностями, последуем за Платоном и ограничим наше исследование двумя делителями 360 и 36 000. Первое является изначально грубым примитивным приближением к количеству дней в году. Отклонение не больше чем на 5 дней практически нечитаемо для целей нумерологии, поэтому легко оправдать Платона за то, что он не обратил на него никакого внимания, как и жившие ранее шумеры и существовавшие до них дикари. Те, кто жили еще раньше, возможно, поступали похоже. Поскольку 360, согласно Платону, пифагорейский или земной год, 36 000 – это 100 таких годов. Но 100 – «законно» квадрат (10 ? 10) божественной декады (10), а следовательно, божественно божественное. Но опять некоторые из пифагорейцев, а возможно, и астрологов-вавилонян утверждали (исходя из первого в наивысшей степени ошибочного предположения по поводу требуемого периода для полного цикла равноденствий), что 36 000 земных лет и есть число, точно соответствующее равноденственному, или космическому, году. Из этого Платон сделал вывод, что полный срок жизни одного человека есть или должен быть 100 земных лет, где каждый год состоит из 360 дней. Из этого вытекает, по словам Платона, что один день в жизни человека равен одному году в жизни вселенной. Человек проживает только короткий отрезок времени, но он проживает этот отрезок быстро.

Даже такие области, как эсхатология, искусство управлять государством и эпистемология, не были оставлены вниманием пифагорейцев, как, разумеется, и должно было быть. В противном случае все сущее не стало бы числом. По одному примеру синтеза по каждому направлению будет достаточным. Первые два неинтересны для истории, в отличие от третьего. Все типичные для философии учителя, без сомнения, были основательно изложены в пропавшей «библии» Филолая.

Во-первых, в «Республике» Платона есть несколько жутковатая нумерология преисподней, о которой рассказывает «бравый парень Эр, сын Армения, памфилиец по рождению». Кто заинтересовался, пусть ищет детали там.

Затем упомянем таинственное число 5040, которое Платон приводит в своих «Законах», где этому числу соответствует количество жителей его идеального города. Всякий, кто учил перестановки и комбинации элементарной алгебры, распознает 5040 как общую сумму различных вариантов положения числа 7 в ряду, скажем, 7 книг на полке. Число равно 1 ? 2 ? 3 ? 4 ? 5 ? 6 ? 7. Записанное в таком виде, оно, к нашему смущению, очевидно раскрывает нумерологические возможности. Проявляется даже сверхсакральное число 7, не говоря уж о женском числе 2, мужском 3, числе справедливости 4, числе здорового тела 5 и совершенном числе 6. Среди прочих значений, представляющих интерес для гражданского уложения, 7 есть число вершин Платона, которые должны быть преодолены для приобретения знаний и мудрости, а в действительности 7 есть сами эти вершины. В этом энциклопедическом числе заключено бесконечно многое. Любой нумеролог космоса насчитает в 5040 точно 60 делителей, в то время как в 60–12, в 12 – совершенное 6, а в 4 – справедливость 4, когда 4 содержит точно 3, а 3 содержит точно женскую 2, которая точно содержит 2, и т. д. 2-2-2-… навеки. На основании указанных фактов можно показать, что Идеальный город заключен в Брачное число и что он вечно возвращается, будучи однажды жестко («четверно») возведенным. Внедрение зодиакального 12 слишком очевидно, чтобы говорить о нем специально. Число 3 представляет Идеальную семью в городе в течение всего Великого года.

Третий пример совсем другого толка. Это ограниченный принцип дихотомии, или последовательного деления на 2, за исключением декадического ограничения до 10 дихотомий, фундаментальный инструмент классической логики от Аристотеля до Средних веков и далее.

В предыдущей главе было указано, что первый шаг в науке – это классификация, как в истории природы деревьев и животных. Дихотомия – один из методов классифицирования сложносоставного вида на более простые подклассы и подвиды, до тех пор пока (если процесс продолжается достаточно долго) исходный вид не будет разделен на подвиды, в которых либо будет только один член, либо ни одного. На каждой стадии по меньшей мере один из подвидов разбивается на два. Теперь все вещи, согласно теории пифагорейцев, делятся на две категории противоположностей, одна из которых относится к числу ограниченных, а другая располагается на стороне неограниченных. Но поскольку декада есть часть вселенной, то должно существовать 10 пар противоположностей. Каждая пара есть дихотомия от Единицы. Например, ни одно тело во вселенной (Единица) не может быть в покое и в движении в любую единицу времени, и каждое тело находится в покое и в движении в любую единицу времени. Следовательно, Покой и Движение составляют пару противоположностей, которые призваны дихотомировать Все, или Единицу. Полная декада противоположностей, как решили пифагорейцы, должна выглядеть следующим образом:

1. Ограниченный – Неограниченный

2. Нечетный – Четный

3. Единственный – Множественный

4. Правый – Левый

5. Мужской – Женский

6. Покой – Движение

7. Прямой – Непрямой

8. Свет – Тьма

9. Добро – Зло

10. Квадрат – Овал

После того как несколько примеров пифагорейской науки были продемонстрированы, должно стать очевидным, что дихотомированная декада содержит неограниченные возможности для нумерологии в науке, философии и чистом разуме. Многие из них были выработаны нумерологами и логиками Античности и Средних веков. Миллионы человеко-часов и тысячи жизней растрачены ради этой беспредельной задачи, цели которой ни один здравствующий ныне человек не сможет определить. Весь проделанный труд оставил лишь небольшой сухой остаток в тривиальных тонкостях логики, которая долгое время представляла лишь антикварный интерес только для тех немногих, кто действительно помнит о ее существовании. И в то время как все это, несомненно, неплодородное поле деятельности культивировалось со страстью почти уникальной в истории человеческой мысли, куда более потенциально урожайное поле деятельности экспериментальной науки, о которой Пифагор также упоминал, лежало невозделанным и запущенным.

За этот неправильный выбор области приложения (если при последнем обследовании его сочтут таковым) Пифагор ответствен в первую очередь. Когда он открыл законы музыкальных интервалов, перед ним расстилались два пути. Один вел обратно в потемки мистицизма и суеверий, а другой – вперед к неоткрытым возможностям экспериментальной науки. Сделав первый шаг в неизвестном направлении, Пифагор внезапно повернулся и пошел старым избитым путем в прошлое. Но он не всегда двигался назад, подобно некоторым из его учеников. Если в своих слишком амбициозных попытках создать сложную науку о вселенной уровень его мышления был донаучным, подобное нельзя сказать о его вкладе в традиционную математику. Только из-за фанатичных стараний Пифогора подчинить все возможное, от звезд до гуманистических ценностей, власти чисел, его мышление оказалось донаучным и дологическим. В этом плане его интеллектуальная активность оказывалась отброшенной назад к каменному веку. Примитивность столь длительных сумерек между абсолютной дикостью и примитивной цивилизацией была не менее суеверной перед лицом природы, чем сам Пифагор со своей лучезарной мечтой о том, что бесконечная сложность природы проста, как арифметика для детей. И это стало его последним открытием. Дороги по-прежнему не выбраны. По какой пойдем мы? Возможно, это окажется не столь важно, когда настанет конец путешествия и мы приляжем отдохнуть в холодных лучах заходящего солнца. Но какой бы путь мы ни избрали, мы будем слишком холодными и равнодушными, если не почувствуем хоть немного того тепла, которое согревало первых поверивших в рациональность мироздания. Только одно в вечном потоке, кажется, остается неизменным, является ключом к единству, к Единице в хаосе многообразия и смятения Многого. Два огня, две планеты, двое родителей – это просто разные аспекты одного неизменного числа при неизменности вечного. Если число не было по-настоящему Богом, откуда же взялись бы силы создавать или разрушать других. Число правит космосом с неподкупной справедливостью, более беспристрастной, чем та, которую проявляют целые пантеоны капризных богов. Только число в одиночку держалось против ветра в утверждении: «Нет ничего постоянного». Оно одно выдюжило и существует, все остальное стало временным проявлением и иллюзией. Все сущее стало числом только в том смысле, что рождало понимание, а для понимания всего сущего, от движения планет до воплощения суда Божьего, необходимо и достаточно понять число.

Это была великая мечта, простая, как детство, но великая, и она не погибла. Но она была только мечтой, и ее возвращение в наши дни не может ничего добавить.