4. Новатор бесконечности Мадхава из Сангамаграмы

^{Ириннараппилли (или Ириннинавалли) Мадхава}

^{Родился: Сангамаграма, Керала, Индия, 1350 г. Умер: Индия, 1425 г.}

«Вода урагана Рита весила, как 100 миллионов слонов». Сегодня СМИ часто используют слонов как меру веса, не говоря уже о Бельгии и Уэльсе как мерах площади, олимпийских плавательных бассейнах как мерах объема и лондонских автобусах для измерения длины или высоты. А что вы скажете о таком перечне:

Боги (33), глаза (2), слоны (8), змеи (8), огни (3), качества (3), веды (4), накшатры (27), слоны (8) и руки (2) – мудрые говорят, что такова мера длины окружности, когда диаметр ее равен 900 000 000 000.

Что первым приходит в голову? На самом деле это перевод стихотворения о числе ?, написанного около 1400 г. Мадхавой из Сангамаграмы – величайшим, вероятно, средневековым индийским математиком и астрономом. Боги, слоны, змеи и т. п. – это символические обозначения чисел, которые предполагалось рисовать в виде маленьких картинок. Вместе (с конца, по списку) они представляют число

282 743 388 233.

При делении на 90 млрд получается

3,141592653592222…

Это, пожалуй, выглядит более знакомо. Отношение, о котором идет речь, представляет собой геометрическое определение числа ?, равного

3,141592653589793…

Эти два числа совпадают до 11-го знака после запятой (округляя 589 до 59 на 10-м и 11-м месте). В то время это было одним из лучших известных приближений. К 1430 г. персидский математик Джамшид аль-Каши побил этот рекорд, получив в своей книге «Мифтах аль-хисаб» («Ключ к арифметике») 16 знаков после запятой.

До нас дошли кое-какие астрономические тексты Мадхавы, но его математические работы известны только в изложении позднейших комментаторов. Вечная проблема приписывания великому основателю и учителю результатов, полученных его интеллектуальными потомками (так, к примеру, все открытое любым членом пифагорейского культа по умолчанию приписывается Пифагору), означает, что мы не можем с полной уверенностью сказать, какие результаты были получены непосредственно Мадхавой. В дальнейшем рассказе я буду принимать слова его последователей на веру.

Его величайшим достижением было введение бесконечных рядов; таким образом были сделаны первые шаги в направлении математического анализа. Он обнаружил то, что известно на Западе как ряд Грегори для функции арктангенса и ведет к выражению числа ? в виде бесконечного ряда. Самые впечатляющие его открытия – бесконечные ряды для тригонометрических функций синуса и косинуса, которые на Западе были найдены только Ньютоном, на 200 с лишним лет позже.

* * *

О жизни Мадхавы известно мало. Он жил в селении Сангамаграма, и это название по традиции добавляется к его имени, чтобы отличать от других людей с именем Мадхава, таких как астролог Видья Мадхава. В селении был храм, посвященный одноименному богу. Считается, что располагалось это селение возле современного селения браминов Ириньялакуда. Это недалеко от города Кочина в штате Керала – длинной вытянутой области на южной оконечности Индии, зажатой между Аравийским морем на западе и горной цепью Западные Гаты на востоке. Во времена позднего Средневековья Керала был крупным центром математических исследований. Большинство раннеиндийских математиков происходили из более северных мест, но по неведомой причине Керала в какой-то момент перехватил инициативу. Математику в Древней Индии, как правило, рассматривали как часть астрономии, и Мадхава основал Керальскую школу астрономии и математики.

В эту школу входило большое количество необычайно сведущих математиков. Парамешвара – индийский астроном, который использовал наблюдение затмений для проверки точности вычислительных методов того времени. Он оставил после себя по крайней мере 25 рукописей. Келаллур Нилаканта Сомаяджи в 1501 г. написал значительный астрономический трактат «Тантрасамграха», состоящий из 432 стихов на санскрите, объединенных в восемь глав. В частности, он включает поправки Нилаканты к теории движения Меркурия и Венеры великого индийского математика Арьябхаты. Он написал также обширный комментарий «Арьябхатия бхасья» на другой труд Арьябхаты, в котором обсуждаются алгебра, тригонометрия и бесконечные ряды для тригонометрических функций. Естхадева написал «Юктибхасу» – комментарий к «Тантрасамграхе», в который добавлены доказательства ее основных выводов. Некоторые считают этот текст первым трудом по дифференциальному исчислению. Мельпатур Нараяна Бхаттатир – математический лингвист – расширил в труде «Пркриясарвавом» аксиоматическую систему Панини из 3959 правил для санскритской грамматики. Прославился он «Нараяниямой» – похвальной песней Кришне, которая поется в Индии до сих пор.

* * *

Тригонометрия, или использование треугольников для измерения, восходит еще к древним грекам; особенно много ей занимались Гиппарх, Менелай и Птолемей. Есть две основные области применения тригонометрии в деятельности человека: топография и астрономия. (Позже к этому списку добавилась навигация.) Существенно здесь то, что расстояния зачастую трудно (а в случае астрономических тел просто невозможно) измерять непосредственно, зато углы можно измерять везде, где есть прямая видимость. Тригонометрия дает возможность вычислить длины сторон треугольника по его углам, при условии что хотя бы одна сторона известна. В топографии одна тщательно измеренная доступная база и множество углов ведут к появлению точной карты; то же, с некоторыми нюансами, относится и к астрономии.

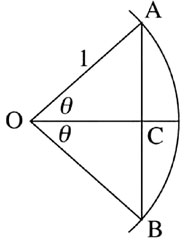
^{Пусть AB - дуга окружности радиуса 1 с центром в точке O. Хорда угла AOB (величина которого составляет 2?) есть длина отрезка AB. Синус угла AOC (величина которого равна ?) равен длине отрезка AC. Косинус угла ? равен длине отрезка OC, а тангенс - отношению AC/OC.}

Греки использовали в своих задачах хорду угла (см. рисунок). Гиппарх в 140 г. до н. э. составил первую таблицу хорд и пользовался ею как в плоской, так и в сферической тригонометрии. Последняя имеет дело с треугольниками, образованными дугами больших кругов на сфере, и это важно в астрономии, поскольку звезды и планеты при наблюдении с Земли кажутся лежащими на небесной сфере – воображаемой сфере, в центре которой находится Земля. Точнее говоря, направления на эти тела соответствуют точкам на любой подобной сфере. Во II в. Птолемей включил таблицы хорд в свой «Альмагест», и его результаты широко использовались на протяжении следующих 1200 лет.

Математики Древней Индии, опираясь на работы греков, добились больших успехов в тригонометрии. Они обнаружили, что удобнее использовать не хорды, а тесно связанные функции синуса (sin) и косинуса (cos), которыми мы пользуемся и сегодня. Синусы впервые появились в «Сурья сиддханта» – серии индийских астрономических текстов, датируемых примерно 400 г.; Ариабхата около 500 г. развил эту идею в своем труде «Ариабхатия». Аналогичные идеи возникли независимо и в Китае. Индийскую традицию продолжили Варахамихира, Брахмагупта и Бхаскара Ачарья, в работах которых имеются полезные аппроксимации функции синуса и некоторые базовые формулы, такие как

sin²? + cos²? = 1

у Варахамихиры; по существу, это тригонометрическая интерпретация теоремы Пифагора.

До недавнего времени ученые считали, что после Бхаскара Ачарья в индийской математике наступил застой, во время которого ученые ограничивались лишь комментариями к классическим работам, и лишь после того, как Британия присоединила Индию к своей активно развивающейся империи, там появилась новая математика. Возможно, это было правдой в отношении значительной части Индии, но не в отношении Кералы. Джозеф отмечает, что «качество математики, доступной в текстах [Керальской школы] … настолько высокого уровня в сравнении с тем, что было достигнуто в классический период, что кажется невозможным, чтобы одно произошло от другого». Однако сколько-нибудь сравнимые идеи появились лишь несколькими столетиями позже в Европе, так что никакого правдоподобного «недостающего звена» разглядеть не удается. Достижения Керальской школы, судя по всему, были ее собственными.

Комментарий Естхадевы «Юктибхаса» так описывает ряд, приписываемый Мадхаве:

Первый член есть произведение заданного синуса и радиуса искомой дуги, деленного на косинус этой же дуги. Последующие члены получаются методом повторений, когда первый член последовательно умножается на квадрат синуса и делится на квадрат косинуса. Все члены затем делятся на нечетные числа 1, 3, 5, … Дуга получается прибавлением и вычитанием соответственно членов с нечетными номерами и членов с четными номерами.

В современной нотации и с учетом того, что тангенс угла ? равен синусу этого угла, деленному на его же косинус, получаем

? = tg? - 1/3 tg³? + 1/5 tg⁵? - 1/7 tg⁷? + ...

Это (если записать в терминах арктангенса) и есть то, что мы на Западе называем рядом Грегори, его открыл в нашей цивилизации Джеймс Грегори в 1671 г. или, возможно, чуть раньше. Согласно трактату «Махаджьянаяна пракара» («Методы для больших синусов»), Мадхава использовал этот ряд для вычисления ?. Особый случай (? = ?/4 = 45°) приведенного ряда дает бесконечный ряд для ? – первый пример рядов такого типа.

?/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ...

Это не слишком практичный способ вычислить число ?, поскольку члены ряда убывают очень медленно и нужно пройти громадное число слагаемых, чтобы получить хотя бы несколько очередных десятичных знаков. Приняв вместо этого ? = ?/6 = 30°, Мадхава вывел вариант ряда, который сходится быстрее:

? = ?12 (1 - 1/3?3 + 1/5?3² - 1/7?3³ + ...).

Он вычислил первый 21 член ряда и получил ? с точностью до 11 знаков после запятой. Этот ряд стал первым новым методом вычисления ? после Архимеда, использовавшего все более близкие по форме к окружности правильные многоугольники.

Один из приемов Мадхавы удивительно хитроумен. Мадхава оценил ошибку, возникающую при усечении ряда на некотором конечном этапе. Мало того, он привел три выражения для ошибки, которые можно прибавлять к общему значению в качестве корректирующего члена для повышения точности. Вот его выражения для ошибки после сложения n членов ряда:

1/4n; n/4n²+1; n²+1/4n³+5n.

Третье из этих выражений он использовал для получения улучшенного значения суммы при расчете ? с точностью до 13 знаков после запятой. Ничего подобного не наблюдается нигде в математической литературе до нынешних времен.

В 1676 г. Ньютон написал письмо Генри Олденбургу – секретарю Королевского общества; в письме он информировал этого достойного человека о двух бесконечных рядах для синуса и косинуса:

 sin? = ? - ?³/3! + ?⁵/5! - ?⁷/7! + ?⁹/9! - ?¹¹/11! + ...

cos? = 1 - ?²/2! + ?⁴/4! - ?⁶/6! + ?⁸/8! - ?¹⁰/10! + ...

которые он вывел кружным путем, с использованием дифференциального исчисления. Сегодня мы знаем, что эти выражения, долгое время приписывавшиеся Ньютону, были получены Мадхавой почти на 400 лет раньше. Подробности вывода этих рядов приведены в «Юктибхасе». Метод вывода сложен, но его можно рассматривать как ранний вариант метода интегрального исчисления – суммирование подобных рядов член за членом.

В самом деле, утверждается, что Мадхава выработал некоторые базовые понятия дифференциального и интегрального исчисления задолго до Ньютона. Речь идет о дифференцировании, интеграле как площади под кривой и почленном интегрировании. Он нашел методы разложения многочленов в алгебре, вывел числовой метод решения уравнений посредством итераций и работал над бесконечными цепными дробями.

* * *

Джозеф спрашивает, могли ли идеи Мадхавы просочиться в Европу. Он указывает, что европейские исследователи, такие как Васко да Гама, хорошо знали Кералу, потому что это удобный остановочный пункт для кораблей, пересекающих Аравийское море на пути в Китай и другие страны Востока. Роль этого региона как центра торговли восходит еще к вавилонским временам. Географическая изоляция, зажатость между Западными Гатами и Аравийским морем, защищала его от бурной политической жизни остальной части средневековой Индии, что было дополнительным бонусом для чужеземных путешественников. Действительно, создается впечатление, что кое-что из достижений керальской техники и местных изделий в то время добиралось до Европы, однако до сих пор не найдено никаких свидетельств прямого переноса математических идей. Так что до тех пор, пока на свет не появятся новые свидетельства (если появятся), нам остается предполагать, что Керала и Европа открыли множество важных математических идей независимо друг от друга.

Работа таких выдающихся индийских математиков, как Ариабхата и Брахмагупта, давно признана в Европе. С трудами Керальской школы европейское научное сообщество впервые познакомилось только в 1835 г., когда Чарльз Виш написал статью о четырех самых значительных индийских текстах: это «Тантрасамграха» Нилаканты, «Юктибхаса» Естхадевы, «Карана Паддхати» Путхуманы Сомайаджи и «Садратнамала» Санкары Вармана. Виш, можно сказать, запустил лису в курятник, когда заявил, что «Тантрасамграха» содержит основы работы с производными, как Ньютон называл дифференциальное исчисление (глава 7): что в ней «полно производных форм и рядов, которые невозможно найти ни в одном труде других стран». В дни, когда всю торговлю с Индией контролировала Ост-Индская компания, а сама страна рассматривалась как легкая добыча для завоевателя, это заявление не произвело совершенно никакого впечатления. Керальская математика была быстро и прочно забыта. Только столетие спустя, в 1940-х гг., ее высокий уровень был наконец вновь описан в серии статей Кадамбура Раджагопала и его соавторов; они проанализировали математику Керальской школы и продемонстрировали, что индийские математики открыли множество важных вещей намного раньше европейцев, которым эти достижения, как правило, приписывали.