Глава 9 ОТ ЧИСЛОВОЙ ОСИ К ЧИСЛОВОЙ ПЛОСКОСТИ

Вводим число «i»

До сих пор при обсуждении квадратных корней я старательно избегал упоминания об отрицательных числах. Например, я говорил, что ?4 = 2, потому что 2 ? 2 = 4. Но точно так же справедливо выражение ?4 = -2, потому что (-2) ? (-2) = 4. (Надеюсь, вы не забыли, что при перемножении двух отрицательных чисел мы получаем положительное число.)

Следовательно, у числа 4 есть два квадратных корня, выражение можно записать следующим образом: ?4 = ±2. Символ «±» обозначает «или плюс, или минус».

Но если оба числа, + 2 и -2, являются корнями квадратными из 4, то какое же число будет корнем квадратным из -4? Конечно, +2 ? -2 = -4, но +2 и -2 — это не одно и то же. Так что перемножение этих двух разных чисел не является возведением в квадрат.

Очевидно, что среди положительных и отрицательных чисел не существует такого, которое, будучи возведено в квадрат, дало бы -4 или любое другое отрицательное число, но давайте проявим упорство, попробуем найти подходящее число и решить эту задачу.

Для начала упростим задачу, насколько это возможно. Любое число, скажем ?64 , можно разбить на множители и записать в виде ?(16?4). Это выражение можно дальше преобразовать в ?16 ? ?4. При этом окончательный ответ не меняется. ?64 = 8 и ?16 ? ?4 = 4 ? 2 = 8.

Мы можем решить еще сколько угодно подобных примеров, и всегда это правило будет справедливо. То есть если число разбить на множители, то квадратный корень из этого числа будет равен произведению квадратных корней сомножителей. Это утверждение справедливо и для иррациональных чисел. Например, ?15 = ?5 ? ?3. Можно заглянуть в специальные таблицы и найти там -?15, равный 3,872983.

В свою очередь, ?5 = 2,236068, ?3 = 1,732051 (конечно, это приближенные значения). При перемножении 2,236068 ? 1,732051 получаем 3,872983, то есть мы доказали, что ?15 = ?5 ? ?3.

Отлично, тогда мы можем предложить такую схему. Любое отрицательное число равно произведению соответствующего положительного числа на -1. Другими словами, -64 = 64 ? (-1); -276 = 276? (-1); -1,98 = 1,98 ? (-1) и так далее.

Квадратный корень из любого числа, например из -172, можно разбить на сомножители: ?-172 = ?172 ? ?-1. Следовательно, если мы найдем квадратный корень из -1, мы сможем найти квадратный корень любого отрицательного числа. Но тут мы опять сталкиваемся с неразрешимой, казалось бы, задачей:

1 ? 1 = 1; (-1) ? (-1) = 1.

Не существует такого числа, которое при перемножении на себя самое дало бы -1.

Следовательно, единственное, что мы можем сделать, — это придумать такое число, Мы можем договориться, что символ # обозначает, что # ? # равно отрицательному числу. Тогда #1 ? #1 = -1. Это выражение справедливо по определению, а поскольку оно не противоречит ни одному из математических постулатов, то нет никаких оснований, чтобы его не использовать.

Разумеется, такое число является нереальным, воображаемым. Мы легко можем себе представить, что такое +$1 и -$1. +$1 — это доход в $1, а -$1 — это расход в $1. Но как представить себе #1$? Математики, которые первыми стали работать с этими новыми числами, назвали их мнимыми. В отличие от мнимых чисел обычные отрицательные и положительные числа, как рациональные, так и иррациональные, называются действительными.

Математики не стали изобретать для этих чисел нового знака, наподобие знака + или -, хотя мне кажется, это было бы целесообразно. Вместо этого они обозначили ?-1 буквенным символом «i». Другими словами, i ? i = -1, или ?-1 = i. Кроме того, -i ? -i также равняется i², то есть -1. Мы также должны записать ?-1 = -i.

И последнее, -i ? i = -i² = -(-1) = 1.

Теперь мы легко можем извлечь квадратный корень из любого отрицательного числа.

Величина ?-4 равна ?4 ? ?—1, или ±2 ? i, что можно просто записать как ±2i.

Точно так же величина ?-64 равна ?64 ? ?-1, или ±8 ? i, что можно просто записать как ±8i, а величина ?-15 равна ?15 ? ?-1, или ±3,8729832 ? i, что можно просто записать как ±3,8729832i.

Числа и координаты по компасу

Однако теперь у нас есть отличный повод для возмущения. Что бы там ни говорили, как бы ни уславливались, совершенно непонятно, что такое эти мнимые числа, как можно их себе представить.

На самом деле такое число должно обозначать то, что мы ему приписали, то, о чем мы условились заранее. Не надо забывать, что числа — это изобретение человека и их цель — облегчить познание Вселенной, а со своими созданиями человек вправе поступать так, как считает нужным.

Вспомним, что у древних греков не было отрицательных чисел. Для них -1 была не менее таинственна и непонятна, чем для нас ?—1, когда мы приступили к изучению мнимых чисел. Обратившись к отрицательным числам, мы использовали числовую ось, на которой вверх от нулевой отметки располагались положительные числа, а вниз — отрицательные (см. главу 2).

Такая схема сработала в прошлый раз, попробуем использовать ее и сейчас. Проведем через нулевую отметку еще одну линию, перпендикулярную первой числовой оси. Справа отложим через равные интервалы + li, +2i, +3i, +4i, +5i, +6i, …, а слева -li, —2i, -3i, —4i, —5i, -5i… Мы получили две числовые оси:

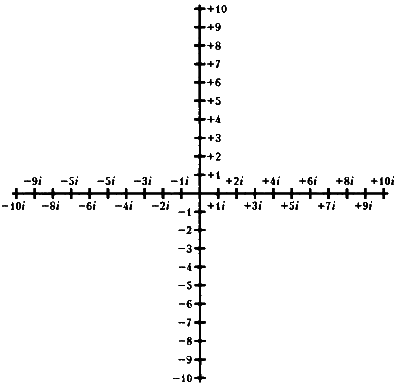
Числовые оси для действительных и мнимых чисел

Например, вместо знаков «+» и «-» мы можем использовать буквенные обозначения сторон света, как на компасе. Условимся, что положительные действительные числа — это N-числа, отрицательные действительные числа — это S-числа, положительные мнимые числа — это W-числа, а отрицательные мнимые числа — это Е-числа.

В нашей схеме совсем не нужно использовать странный термин «мнимое число», поскольку у нас все стороны света — реальны. Но у этого термина глубокие исторические корни, и теперь, пожалуй, поздновато менять название.

Теперь, используя «числа по компасу», мы можем создать свою собственную самодостаточную систему расчетов (создание такой эффективной системы — это цель многих математиков). Таблица умножения в нашей системе будет иметь такой вид:

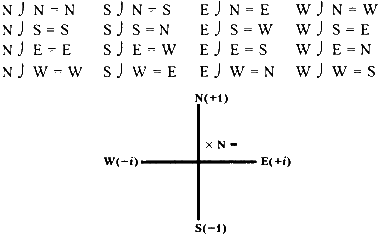
Умножаем на N вращением в направлении 0?

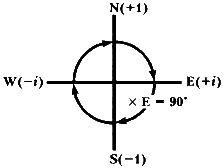
Умножаем на Е вращением на 90° по часовой стрелке

И хотя наша таблица имеет довольно странный вид, у нее есть простое геометрическое толкование, которое представлено ниже на рисунках.

Я совсем не утверждаю, что только наша система справедлива, могут существовать и другие системы, в такой же мере справедливые и наглядные. Просто предложенная система удобна и используется.

Новые точки по компасу

Раз уж мы заговорили о севере, юге, западе и востоке, то следует вспомнить и о таких направлениях, как северо-запад, юго- восток и так далее. Поскольку результат умножения действительных чисел на мнимые никогда не будет ложиться ни на одну из осей (север—юг или восток—запад). А как обстоят дела со сложением, например, чему равна сумма 1 + i? Ученые-математики не удосужились предложить специальный символ для этого выражения, поэтому его оставляют в виде 1 + i, но в нашей системе координат его можно представить наглядно.Теперь, используя «числа по компасу», мы можем создать свою собственную самодостаточную систему расчетов (создание такой эффективной системы — это цель многих математиков). Таблица умножения в нашей системе будет иметь такой вид:

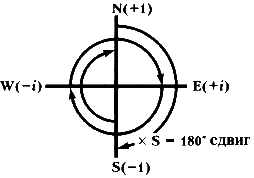
Умножение на S вращает ось на 180°

E ? S = W

S ? S = N

W ? S = E

N ? S = S

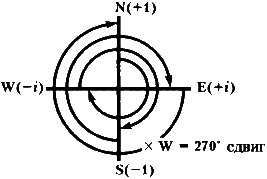
Умножение на W вращает ось на 270°

E ? W = N

S ? W = E

W ? W = S

N ? W = W

N = положительное действительное число, например +1.

Е = положительное мнимое число, например +i.

S = отрицательное действительное число, например —1.

W = отрицательное мнимое число, например —i.

Теперь давайте снова построим две оси, но вместо того, чтобы проставлять значения против каждого деления, на этот раз проведем через каждое деление новую линию.

Предположим, через каждое деление на вертикальной оси, то есть на оси действительных чисел, мы проводим горизонтальную линию. Проводим линию через деление +1, и на всей протяженности этой линии значение действительного числа равно +1. Следующую горизонтальную линию проводим через +2, и на всей протяженности этой линии значение действительного числа равно +2. Следующую горизонтальную линию проводим через -3, и на всей протяженности этой линии значение действительного числа равно -3. Таких линий можно провести сколь угодно много.

Такую же процедуру можно осуществить и с горизонтальной осью, то есть с осью мнимых чисел. Через каждое деление на горизонтальной оси, то есть на оси мнимых чисел, мы проводим вертикальную линию. Так же, как и в прошлом случае на всей протяженности линии, проведенной через деление +1i, значение мнимого числа равно +1i; на всей протяженности линии, проведенной через деление +2i, значение мнимого числа равно +2i; а на всей протяженности линии, проведенной через деление -5i, значение мнимого числа равно -5i.

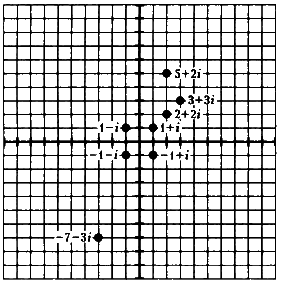
Комплексные числа

Теперь мы получили своеобразный шаблон шахматной доски, на котором для каждой линии, соответствующей мнимому числу, существует линия, соответствующая действительному числу, и наоборот, причем эти линии пересекаются.

Теперь мы сможем найти ответ на вопрос, чему равна сумма 1 + i. Число, соответствующее 1 + i, — это точка пересечения линий +1 и +i на нашем шаблоне. Поскольку расстояния между делениями на обеих осях одинаковы, 1 + i представляет собой число в направлении северо- восток. Точно так же и 2 + 2i, 3 + 3i, 4 + + 4i и так далее.

Число, подобное числу 1 - i, можно представить как +1 + (-i), и оно будет на нашем шаблоне представлять собой точку пересечения прямых +1 и -i, то есть в направлении северо-запад. Точно так же -1 + i — это юго-восток, а -1 - i — это юго-запад.

Другие направления можно представить такими числами, как 15 + 2i, -7 - 3i и так далее. По сути дела, каждая точка на нашем шаблоне (который, как вы уже догадались, можно расширять бесконечно) представляет собой какое-то число, которое является суммой действительного и мнимого числа. Более того, положение точки на шаблоне может соответствовать выражению, содержащему десятичную дробь или иррациональное число, например 9,54 + 0,015i, или 2?7 + -5?2i.

Числа, подобные тем, что представлены выше, состоящие из действительной и мнимой частей, называются комплексными. Любое действительное или мнимое число может быть представлено в виде комплексного, то есть 42 = 42 + 0i, a 5i = 0 + 5i.

Комплексные числа представляют интерес не только для инженеров и ученых, они представляют и чисто практический интерес в обыденной жизни, поскольку, в отличие от обычных чисел, указывающих только величину, они указывают также и направление.

Приведем пример, который продемонстрирует вам роль комплексных чисел. Рассмотрим такое физическое понятие, как сила. Сила может представлять собой толкающее усилие или тянущее усилие. Толкающее усилие — это положительная величина, тянущее — отрицательная. Кроме того, сила может изменяться по величине. Таким образом, мы можем использовать для величины силы действительные числа.

Но, кроме того, сила может быть направлена в разных направлениях. И толкающее усилие, и тянущее усилие могут быть направлены вверх, вниз, вбок и так далее. Выразить величину силы с учетом направления можно при помощи комплексных чисел. Таким образом, число i, которое большинству людей, не связанных с математикой, представляется таинственным, но совершенно бесполезным понятием, имеет простое практическое применение. Например, в области электроники никакая математическая обработка данных невозможна без применения комплексных чисел. Величина переменного тока меняется как по величине, так и по направлению, и для ее описания необходимо использовать комплексные числа.

Комплексные числа можно складывать и вычитать по таким же правилам, как обычные числа, причем действительные и мнимые числа складываются и вычитаются отдельно. Например, если к (+2 - 4i) прибавить (-5 + 7i), то получим (-3 + 3i). Если из ( + 2 - 4i) отнять (-5 + 7i), то получим (-7 + 11i). (Это можно продемонстрировать на нашем шаблоне, так как обычное сложение и вычитание можно показать на оси север-юг. Думаю, что теперь вы сможете это сделать самостоятельно.)

Вот при умножении комплексных чисел мы столкнемся с большими трудностями, чем в случае умножения действительных чисел. При умножении 35 на 28, как я вам уже объяснил в третьей главе, мы разбиваем числа на разряды, то есть 35 = = 30 + 5, 28 = 20 + 8. Затем числа перемножаются, каждое слагаемое одной части на каждое слагаемое другой части, а результаты умножения складываются.

Точно так же производят операцию умножения с комплексными числами. Для того чтобы умножить (3 + 5i) на (6 + i), нужно составить такую схему:

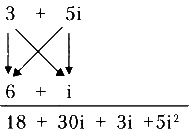
Стрелками показано, как перемножаются составные части комплексных чисел. В соответствии со схемой:

3 ? 6 = 18, 3 ? i = 3i, 5i ? 6 = 30i и 5i ? i = 5i² = -5, поскольку i² равно -1.

Два из промежуточных результатов являются действительными числами, и их можно сложить, то есть 18 — 5 = 13. Другие две составляющие являются мнимыми числами, и их также можно сложить: 30i + 3i = 33i. Таким образом, результатом умножения является комплексное число 13 + 33i.

Другие арифметические операции также можно продемонстрировать при помощи аналогичной схемы. Таким образом, мы видим, что с комплексными числами можно работать по тем же правилам, что и с обычными числами, а значит, комплексные числа больше не являются для нас таинственными и непостижимыми.

Докапываемся до корней.

Уходим дальше вглубь

Область комплексных чисел дает возможность рассмотреть некоторые сложные случаи при извлечении корней степени больше 2.

Мы с вами уже знаем, что ?+1 равен +1 или -1, ?-1 равен + i или -i.

А чему равен корень четвертой степени из +1 (⁴?+1)? Очевидно, что (+1) ? (+1) ? (+1) ? ( + 1) = +1, то есть +1 — это один из корней четвертой степени из +1. Точно так же (-1) ? (-1) ? (-1) ? (-1) = +1, то есть +1 — это также один из корней четвертой степени из +1. Но мы еще не перебрали все варианты. Как насчет выражения (+i) ? (+i) ? (+i) ? (+i)? Результат перемножения (-i) ? (-i) — это -1. Следовательно, (-i) ? (-i) ? (-i) ? (-i) = (-1) ? (-1) = +1. Это означает, что +i — это третий корень четвертой степени из +1. Точно так же мы можем показать, что —i — это четвертый корень четвертой степени из +1.

Следовательно, наша задача имеет следующий ответ: (⁴?1) = +1, -1, +i, -i. Точно так же мы можем показать, что (⁴?-1) равен +?+i, -?+i, +?-i, или -?-i, то есть эта задача имеет четыре равноценных решения.

А что же такое ?+i? Ответ прост. (?+i) — это такое число, которое, будучи умножено на себя самое, дает i. Поэтому (+?+i) ? (+?+i) = +i Следовательно, (+?+i) ? (-?+i) ? (+?-i) ? (-?-i) = (+ i) ? (+ i) = -1.

Следовательно, (+?+i) является одним из корней четвертой степени из (-1), другими корнями являются -?+i, +?-i и -?-i.

Точно таким же образом можно показать, что любое число имеет четыре корня четвертой степени.

Мы показали, что каждое число имеет два квадратных корня и четыре корня четвертой степени. Можно предположить также, что каждое число имеет три корня третьей степени, пять корней пятой степени, шесть корней шестой степени, сорок пять корней сорок пятой степени и так далее. Это утверждение абсолютно верно, но чтобы его доказать, потребуется сложный математический аппарат, которым мы не владеем, поэтому пока примем его на веру.

Правда, мы можем проверить это утверждение для корня третьей степени. Чему, например, равен корень кубический из 1, или (³?+1)? Во первых, (+1) ? (+1) ? (+1) = +1, то есть +1 является одним из кубических корней из 1.

А чему равны остальные два? Перейдем в область отрицательных чисел.

(-1) ? (-1) ? (-1) = ( + 1) ? (-1) = -1

Таким образом, -1 не является корнем кубическим из 1. Более того, можно показать, что ни одно действительное число, а также ни одно мнимое (будь то -i или -И), возведенное в третью степень, не дает в результате + 1.

Значит, корень всего один, а других двух просто нет?

Эти два корня существуют, но в области комплексных чисел. Я просто приведу их значения, а вы сможете проверить, чему равны эти числа, возведенные в куб. Остальные два корня кубических из + 1 — это (-1/2 + 1/2?3i) и (-1/2 - 1/2?3i). Давайте проверим это утверждение.

Если (-1/2 + 1/2?3i) — один из кубических корней +1, то это значит, что (-1/2 + 1/2?3i)³ или (-1/2 + 1/2?3i) ? (-1/2 + 1/2?3i) ? (-1/2 + 1/2?3i) равно 1. Умножение можно произвести по той методике, которая описана выше.

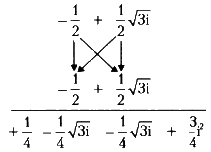
Два промежуточных мнимых результата можно сложить, сумма чисел (-1/4?3i) и (-1/4?3i) равна (-1/2?3i). Что касается 3/4i², то это действительное число, равное -3/4.Теперь сложим два действительных составляющих этого выражения: 3/4 - 1/4 = -1/2, таким образом, результат умножения -1/2 - 1/2?3i.

Этот результат нужно снова умножить на (-1/2 + 1/2?3i).

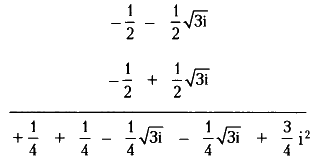
Две мнимые составляющие этого выражения (-1/4?3i) и (-1/4?3i) в сумме дают 0, так что ими можно пренебречь. Число 3/4i² является действительным числом, так как i² = -1, то есть 3/4i² = -3/4. Добавим к 3/4оставшийся промежуточный результат 1/4 и получим 1. Итак, (-1/2 + 1/2?3i)³ равно 1.

Точно так же можно возвести в третью степень число (-1/2 - 1/2?3i).

(-1/2 - 1/2?3i) ? (-1/2 - 1/2?3i) ? (-1/2 - 1/2?3i) = 1.

Точно так же можно показать, что у числа -1 есть три корня третьей степени, два из которых комплексные, по три кубических корня и у чисел i и -i.

И не только i

На нашем «шахматном» шаблоне можно изобразить также третью линию, или ось, так, чтобы помимо направлений север, юг, запад и восток у нас появились направления «внутрь» и «наружу». Таким образом, наша «шахматная доска» из плоской фигуры превращается в объемную фигуру. Теперь точно так же, как в свое время мы получили сетку на плоскости, мы можем составить мозаику из кубиков.

Третья ось состоит из гипермнимых чисел, которые обозначаются буквой j. На гипермнимой оси также имеется положительная и отрицательная области, где, соответственно, расположены положительные (+1j, +2j, +3j, +4j, +5j, +6j и т. д.) и отрицательные (-1j, -2j, -3j, - 4j, -5j, -6j и т. д.).

Теперь числа располагаются в пространстве, на точках пересечения плоскостей север—юг, запад—восток и «внутрь» и «наружу». При пересечении этих плоскостей образуются кубы, принцип тот же, что и при образовании квадратов на нашем «шахматном шаблоне». Каждая точка такого пространства имеет собственные координаты, которые являются гиперкомплексным числом.

Нам легко представить себе три оси в пространстве, поскольку это привычные три измерения: длина, ширина и высота. Однако математики оперируют с большим количеством измерений. Иногда они работают даже в таких системах, где точное количество осей не определено. Тогда говорят об «n-мерном пространстве», где n — это любое число.