Глава 4 Компьютеры в XX веке

Глава 4

Компьютеры в XX веке

Бурный XX век стал свидетелем всевозможных изменений в политике, общественной жизни и, разумеется, в науке, которые сопровождались невероятной технической революцией. Эта история великих теорий, потрясающих открытий и горьких разочарований сопровождалась прорывом в области вычислений, благодаря чему стало возможным создание нового цифрового мира. Развитие информатики было поистине удивительным, однако в архитектуре вычислительных машин не произошло значительных изменений. В современных компьютерах по-прежнему используется архитектура фон Неймана.

Серия Z Конрада Цузе

Главными героями в истории информатики и вычислительной техники в XX веке были исключительные личности, которые много лет были никому не известны. Среди них — немецкий инженер Конрад Цузе и его вычислительные машины серии Z. Большинство изобретений Цузе долгое время оставались незамеченными, так как были сделаны незадолго до начала Второй мировой войны, а работа над ними продолжалась в последующие несколько лет. Цузе, сам того не осознавая, следовал идеям Бэббиджа, с работами которого он был совершенно не знаком. Когда Джон фон Нейман позднее описал архитектуру компьютера, он не руководствовался работами Цузе. Несомненно, созданная ими архитектура вычислительных машин была оптимальной: это подтвердили специалисты в области логики. Она содержала устройство управления, память и арифметико-логическое устройство для выполнения вычислений.

Цузе создал две первые машины в период с 1935 по 1939 год, перед самым началом Второй мировой войны. Его первая патентная заявка датирована 11 апреля 1936 года. В 1938 году он подал патентную заявку в США. Она была отклонена, так как Цузе изложил свое открытие недостаточно подробно. Его вычислительные машины назывались Z1 и Z2. Сначала Цузе назвал первую машину VI (от слова Versuchsmodell, что означало «экспериментальная модель»), но затем сменил название, чтобы избежать путаницы с названиями ракет VI и V2 Вернера фон Брауна.

Первая машина Z1 имела размеры 2 х 1,5 метра. Сделанная из стали, она была достаточно ненадежной: поправки требовалось вносить каждые несколько минут. Это был всего лишь двоичный механический калькулятор с ограниченными возможностями программирования, работавший от электричества. Цузе сконструировал Z2, чтобы исправить недостатки первой машины. Для сохранения чисел и представления чисел с фиксированной запятой в ней использовались реле. Позднее, по совету Хельмута Шрайера, Цузе спроектировал машину Z3, в которой использовались электронные лампы. Эта машина работала без сбоев.

Она была представлена в Институте аэродинамических исследований 5 декабря 1941 года. В машине Z3 ввод данных выполнялся с клавиатуры, а управляющая программа записывалась на целлулоидной ленте. В памяти машины можно было сохранять до 64 чисел, представляемых в двоичной системе счисления с плавающей запятой. Для хранения каждого числа использовалось 22 бита: 1 бит для знака, 7 для показателя степени, 14 для мантиссы. Цузе обнаружил, что в представлении числа с плавающей запятой первый бит может быть всегда равным единице — достаточно подобрать соответствующий показатель степени. Эта форма представления чисел используется и сейчас. С ее помощью можно «сэкономить» один бит, который всегда равен единице. Благодаря открытию Цузе машина Z3 могла работать с числами, мантисса которых представлялась 13 битами. Тем не менее эта машина имела одно важное ограничение: в ней не были реализованы условные переходы. Скорость вычислений составляла три-четыре операции сложения в секунду, умножение выполнялось за четыре-пять секунд.

По заказу Института аэродинамических исследований Цузе немедленно приступил к работе над Z4. Окончательный вариант машины был представлен 28 апреля 1945 года. В памяти машины можно было сохранять 1024 32-битных числа. В ней также были реализованы подпрограммы и условные переходы. Кроме того, был реализован механизм чтения двух инструкций, следующих за данной. Таким образом, операции можно было менять местами, если это не влияло на результат, что обеспечивало экономию времени. Эта процедура была реализована в более поздних компьютерах и получила название lookahead («просмотр вперед»).

Перед самым окончанием войны Цузе переехал на ферму в Альпах и начал работу над докторской диссертацией, озаглавленной «Общая теория вычислений». В этой диссертации, завершенной в 1946 году, описывался язык Планкалкюль (от нем. Plankalk?l — «исчисление планов») — протоязык программирования, который тем не менее не был реализован. Планкалкюль был создан для решения числовых и других задач. Для него был характерен высокий уровень абстракции, значительно превосходящий другие языки программирования того времени. Первым языком, который действительно мог с ним сравниться, был Алгол, созданный много лет спустя.

* * *

КОНРАД ЦУЗЕ (1910–1995)

В университетские годы немецкому инженеру Конраду Цузе приходилось выполнять множество расчетов вручную. Он изнывал от скуки и задумался о создании машины, способной помочь ему в расчетах. По окончании университета он начал работать на авиационном заводе, но вскоре оставил работу и занялся постройкой своей машины в доме родителей. Вскоре он создал первый в мире работающий программируемый компьютер. Он создал машины общего назначения серии Z, машины S1 и S2 для выполнения расчетов, связанных с бомбардировками, а также машину L1 для вычисления значений логических функций. Он также разработал язык программирования Планкалкюль, который не вышел за рамки теории. Цузе основал несколько компаний для постройки своих машин. Важнейшей из них стала Zuse KG, силами которой были частично изготовлены машины серии Z. Zuse KG считается первой в истории компьютерной компанией.

* * *

В 1947 году в разрушенной послевоенной Германии Цузе возвращается к работе над своими машинами. Он наладил контакты с IBM, а позднее с Remington-Rand, с которой заключил соглашение. Он создал машины на электронных лампах, в частности Z22, и на транзисторах, в частности Z23 и Z3. Позднее ученый разработал Z64 — графопостроитель, управляемый машиной.

Единственным образцом первых машин Цузе, дошедшим до наших дней, стала Z4 — первая коммерческая вычислительная машина. Она использовалась во множестве учреждений вплоть до 1959 года. Один из экземпляров Z4 вместе с воссозданной версией Z3 сейчас хранится в Немецком музее Мюнхена. К сожалению, все остальные машины были разрушены во время бомбардировок Берлина.

Машина Тьюринга и «Колосс»

Алан Тьюринг (1912–1954) в детстве хотел стать врачом, но в итоге стал математиком, философом и специалистом по криптографии, а также создателем современной информатики. Он известен в первую очередь благодаря своим теоретическим работам, однако также сыграл очень важную роль в практической реализации одного из первых компьютеров. Тьюринг сделал свое первое открытие в теоретической математике в 1936 году, решив проблему разрешения (Entscheidungsproblem), сформулированную Давидом Гильбертом. Чтобы справиться с этой задачей, Тьюринг создал модель вычислений, в которой дал формальное определение алгоритму (или программе). Эта модель вошла в историю под названием машина Тьюринга.

В 1928 году влиятельный немецкий математик Давид Гильберт (1862–1943), который в 1900 году предложил знаменитый список задач, начал работу над проблемой разрешения, которую впервые сформулировал Лейбниц. Гильберт считал, что нерешаемых задач не существует. Он предложил гипотезу, согласно которой всегда можно составить программу (алгоритм), которая сможет дать однозначный верный ответ на любой заданный вопрос. Независимо друг от друга Алан Тьюринг и американский математик Алонзо Чёрч доказали, что Гильберт ошибался: нерешаемые задачи существуют, а предложенную Гильбертом программу (алгоритм) составить невозможно. Следовательно, математика не является разрешимой, то есть не существует метода, который позволил бы определить истинность или ложность произвольного математического утверждения.

Математик Алан Тьюринг, считающийся одним из создателей компьютеров.

Чёрч и Тьюринг в своих доказательствах использовали созданные ими модели: первый применял лямбда-исчисление, второй — разработанную им машину. Оба дали формальное определение алгоритму и использовали в своих доказательствах арифметические задачи. Существование арифметических задач, для которых решения отсутствуют, означало бы, что решить любую произвольную задачу также невозможно. Однако работа Тьюринга была намного более доступной и понятной.

Он свел проблему разрешения к проблеме остановки и доказал, что она неразрешима с помощью его машины: нельзя определить алгоритмически, завершит ли данная машина Тьюринга свою работу в какой-то момент или нет. Чёрч и Тьюринг не соперничали; напротив, оба осознавали, что их модели, несмотря на формальные различия, были одинаково мощными, и объединили усилия.

* * *

КАК РАБОТАЕТ МАШИНА ТЬЮРИНГА?

Представим себе бесконечную ленту, на которой записаны входные символы некой задачи и на которой можно печатать. Машина Тьюринга содержит считывающее устройство, расположенное в определенной части ленты. Это считывающее устройство позволяет выполнять считывание и запись на ленту, а программа машины Тьюринга может перемещать считывающее устройство в заданное положение. Возможные состояния машины представляются посредством множества состояний Q. Программирование машины представляется в виде функции перехода, которая определяет новое состояние на основе текущего состояния и входного символа.

Формально машина Тьюринга определяется на основе кортежа из семи элементов. Кортеж — это упорядоченная последовательность элементов, то есть перечень ограниченного числа объектов. Кортежи используются для описания математических объектов, имеющих структуру. Обозначим кортеж, который будет обрабатывать наша машина Тьюринга, как

МТ = (?, ?, Ь, Q, q₀, f, F).

Его элементы определяются следующим образом.

• ? — алфавит, символы которого записываются на ленте.

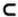• ?  ? — алфавит, символы которого подаются на вход машины. Множество возможных входных символов является подмножеством символов, которые могут быть записаны на ленте. На ленте также будут находиться символы, записанные самой машиной.

• b  ?, Ь   ?: Ь определяет пустое пространство. Это символ, не принадлежащий множеству входных символов. Изначально лента содержит конечное число символов ?; оставшаяся часть ленты (которая является бесконечной) заполнена символами Ь.

• Q — множество состояний.

• q₀   Q — начальное состояние.

• f — функция перехода. Для данного состояния и элемента, записанного на ленте, эта функция определяет новое состояние, записывает символ на ленте и перемещает считывающее устройство влево (I), вправо (D) или же оставляет неподвижным (Р). Таким образом, функция f является функцией вида f: Q x ? —> Q x ? х {I, D, Р}.

F 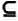 Q — множество конечных состояний.

* * *

В апреле 1936 года американский математик Алонзо Чёрч из Принстонского университета опубликовал работу о проблеме разрешения. Чёрч пришел к тому же выводу, что и Тьюринг, доказав, что не все в математике является вычислимым.

В своем доказательстве он использовал лямбда-исчисление, разработанное им совместно с коллегой Стивеном Клини, которое радикально отличалось от машины Тьюринга. Тьюринг опубликовал свое решение проблемы разрешения в августе того же 1936 года. Это была его знаменитая статья «О вычислимых числах в приложении к проблеме разрешения», в которой были переформулированы результаты Курта Гёделя (1906–1978) о пределах доказуемости и вычислений, а также содержались ссылки на работу Чёрча. Вместо того чтобы спорить, кто совершил открытие первым, в сентябре того же года Тьюринг переходит на работу в Принстонский университет, чтобы написать диссертацию о проблеме разрешения под руководством Чёрча. Он защитил диссертацию в 1938 году, получил степень доктора и вернулся в Кембридж. Этот удачный союз талантов принес немалую выгоду всему человечеству.

* * *

БЛЕТЧЛИ-ПАРК И ЭНИГМА

Легендарное шифровальное подразделение Великобритании Блетчли-парк располагалось в графстве Бакингемшир в 80 километрах от Лондона. Во время Второй мировой войны наиболее авторитетные английские ученые работали в Блетчли-парке над взломом немецких шифров. Это подразделение располагалось в одноименном викторианском поместье (сегодня музей криптографии). В Блетчли-Парке был расшифрован код шифровальной машины «Энигма». Эта машина содержала шифровальный механизм, состоящий из вращающихся роторов и колец, который позволял вооруженным силам нацистской Германии расшифровывать и зашифровывать сообщения. Усилия британских ученых по взлому шифра «Энигмы» не пропали даром: считается, что прочтение предположительно секретных сообщений немцев позволило приблизить окончание войны на несколько лет.

* * *

Эти значимые события, касающиеся наиболее теоретической области науки, происходили в один из самых драматичных моментов современной истории. Политическая ситуация в Европе накалялась, и мир двигался к войне. Опасаясь, что Англия вступит в войну с Германией, Тьюринг во время работы над диссертацией начал заниматься криптографией. Британское правительство в 1939 году пригласило его работать в Блетчли-парке вместе с другими исследователями. Перед ними стояла задача взломать секретный шифр немецкой армии — код «Энигмы». Благодаря своим знаниям Тьюринг смог взломать шифр немецких воздушных сил в середине 1941 года, однако в феврале 1942 шифр был усложнен, и сообщения немцев снова стало невозможно прочесть.

Чтобы расшифровать их, Тьюринг и его коллеги разработали несколько вычислительных машин. Тьюринг еще во время работы в Принстоне изобрел машину, позволявшую выполнять умножение. Группа Тьюринга создала машину под названием «Колосс», которая считается первым электронным программируемым компьютером в мире. Было построено десять экземпляров «Колосса». Первый из них начал работу в декабре 1943 года, на два года раньше, чем американский ENIAC. В конце 1942 — начале 1943 года Тьюринг совершил новую поездку в США, чтобы помочь американским военным взломать немецкие шифры. Во время поездки он познакомился с Клодом Шенноном, создателем теории информации и автором определения энтропии.

После окончания войны Тьюринга пригласили в Национальную физическую лабораторию (National Physical Laboratory), отвечавшую за развитие научно-технических стандартов в Великобритании. Там он разработал ACM (Automatic Computer Machine) — автоматическую компьютерную машину — и сформулировал понятие микропрограммирования как способа задания и изменения команд арифметико-логического устройства. Существует и альтернативный вариант, при котором арифметико-логическое устройство реализовано в оборудовании компьютера и его операции изменять нельзя. Тьюринг также определил понятия подпрограммы и программной библиотеки.

Весь 1947 год он отдыхал в Кембридже, где написал статью, в которой представил нейронную сеть — модель, использующую понятия из физиологии и неврологии. В следующем году, увидев, что работы над автоматической компьютерной машиной остановились, он перешел на службу в Манчестерский университет, где начал работу над программным обеспечением компьютера Mark I Максвелла Ньюмана.

В этот период он создал свои наиболее абстрактные работы. Он написал знаменитую статью «Вычислительные машины и разум», опубликованную в журнале Mind в октябре 1950 года, в которой изложил свою точку зрения на искусственный интеллект и описал знаменитый эксперимент, известный как тест Тьюринга. Целью эксперимента было определить, может ли машина мыслить.

Два оператора работают на «Колоссе» Mark 2.

* * *

ПОСТЫДНАЯ НЕСПРАВЕДЛИВОСТЬ

Математик и логик, который в немалой степени определил облик современного мира, в последние годы жизни подвергся столь постыдному и несправедливому преследованию со стороны полного предрассудков послевоенного британского общества, что это стоило ему жизни. Блестящая карьера Алана Тьюринга прервалась, когда его начали преследовать за нетрадиционную сексуальную ориентацию, которая в то время считалась в Великобритании преступлением. От подобных обвинений за 50 лет до этого пострадал Оскар Уайльд. Тьюринг знал, что ему нечего стыдиться, и начался судебный процесс, широко освещавшийся в прессе. Суд предложил ему выбор между тюремным заключением и гормональной терапией для подавления либидо. Желая избежать тюрьмы, он согласился на лечение, которое продолжалось в течение года, привело к значительным изменениям в организме ученого и сделало его импотентом. После этого Тьюринг покончил жизнь самоубийством, приняв цианид. Еще более примечательно, что в письмах коллегам он выражал беспокойство по поводу того, что эти обвинения бросят тень на его работы по искусственному интеллекту, которые он сам считал крайне важными для всего человечества. В 2009 году Гордон Браун, который в то время занимал пост премьер-министра Великобритании, публично принес извинения от имени британского правительства за преследование, которому подвергся Алан Тьюринг в последние годы жизни. С момента смерти Тьюринга, который оказал неоценимые услуги своей стране и всему цивилизованному миру в борьбе с нацизмом, прошло почти 60 лет.

* * *

В 1951 году он был избран членом Лондонского королевского общества. Однако в конце жизни он не получил того признания, которого заслуживал. В 1966 году, спустя несколько лет после его трагической гибели, Ассоциация вычислительной техники учредила премию, носящую его имя, — премию Тьюринга, которая считается эквивалентом Нобелевской премии в информатике. Среди лауреатов премии — ученые, совершившие выдающиеся открытия в области аппаратного и программного обеспечения, баз данных, теоретических основ информатики (включая криптографию) и компьютерных сетей.

Архитектура фон Неймана

Джон фон Нейман вошел в историю информатики в неспокойный период, во время Второй мировой войны, когда он работал над атомной бомбой в рамках «Проекта Манхэттен». Для проекта требовались новые вычислительные машины, которые в то время становились все более мощными и продвинутыми. Фон Нейман начал поиски ведущих исследователей в области вычислений по всей стране. Он обратился к Джону Пресперу Эккерту (1919–1995) и Джону Уильяму Мокли (1907–1980) из Пенсильванского университета, которые сконструировали компьютер ENIAC (Electronic Numerical Integrator and Computer — электронный числовой интегратор и вычислитель), американский ответ британскому «Колоссу». Они хотели разработать новую, улучшенную машину под названием EDYAC (Electronic Discrete Variable Automatic Computer — электронный автоматический вычислитель с дискретными переменными). В марте 1945 года фон Нейман изложил свои идеи в ставшем знаменитым документе «Первый черновик отчета об EDYAC», автором которого значился он один, что стало причиной разногласий Неймана с Эккертом и Мокли.

В «Первом черновике» была представлена архитектура фон Неймана, описывавшая наиболее эффективное устройство компьютера. В архитектуре фон Неймана программы хранятся во внутренней памяти компьютера, а устройства обработки и хранения данных разделены. Кроме этого, фон Нейман предложил хранить программы и данные в одной и той же памяти в целях экономии. Работа компьютера в архитектуре фон Неймана в общем виде состоит из трех этапов.

1. Извлечение инструкции из памяти.

2. Декодирование.

3. Исполнение.

* * *

ENIAC

ENIAC был завершен и представлен прессе в 1945 году, проработав десять лет до окончательной остановки в 1955 году. Учеными, внесшими основной вклад в его создание, были Герман Хайн Голдстайн, Джон Пресперт Эккерт и Джон Уильям Мокли. Этот огромный компьютер занимал площадь в 63 м², весил 30 тонн и имел 2,6 метра в высоту, 0,9 — в ширину и 26 — в длину. В нем использовалось 18000 электронных ламп, 72000 диодов, 70000 резисторов и 1500 реле. Чтобы построить ENIAC, потребовалось выполнить примерно 5 миллионов соединений ручной пайки. Его стоимость составила почти полмиллиона долларов. В нем отсутствовала память, однако в его 20 накопителях могло сохраняться 20 десятизначных чисел. Переключатели также позволяли сохранять значения функций (104 двенадцатизначных числа). Сложение выполнялось за 0,2 миллисекунды, умножение — за 2,8 миллисекунды. При работе ENIAC температура в машинном зале поднималась до 50 °C. Ходили слухи, что во время его работы в Филадельфии, где располагался компьютер, случались кратковременные отключения электричества, так как он потреблял 160 кВт электроэнергии.

* * *

Таким образом обрабатывались все инструкции, последовательно записанные в памяти компьютера, если только среди инструкций не встречалась инструкция условного перехода. Эта архитектура не слишком отличалась от той, что использовали Чарльз Бэббидж и Конрад Цузе. Эта же архитектура используется в современных компьютерах.

После публикации «Первого черновика» фон Нейман занялся поисками финансирования для постройки более мощной вычислительной машины. Этой машиной стал ADIVAC, разработанный в IAS (Institute for Advanced Study — Институт перспективных исследований) в Принстоне в 1953 году.

* * *

ДЖОН ФОН НЕЙМАН (1903–1957)

Американец венгерского происхождения Джон фон Нейман — одна из ключевых фигур в науке XX столетия. Он был пионером современных цифровых вычислений и совершил открытия во многих областях: квантовой физике, кибернетике, экономике и, разумеется, математике. Фон Неймана называли вундеркиндом; в 1926 году, когда ему было всего 23 года, он получил степень доктора математики, защитив диссертацию по аксиоматике теории множеств. В Европе он занимался исследованиями в области математики и квантовой механики.

Он преимущественно работал в Гёттингене под руководством Давида Гильберта и написал книгу ««Математические основы квантовой механики» на немецком языке. В 1930 году Нейман эмигрировал в США, в возрасте 29 лет занял одну из пяти первых профессорских должностей в принстонском Институте перспективных исследований. Еще одну из этих должностей занимал Альберт Эйнштейн. Фон Нейман считается создателем теории игр и автором понятия MAD (Mutually Assured Destruction — «Взаимное гарантированное уничтожение»). Он работал над Манхэттенским проектом и созданием водородной бомбы.

* * *

Первые компьютеры в США

ENIAC как компьютер общего назначения был огромным шагом вперед, однако некоторые технические решения, использованные при его постройке, оставляли желать лучшего. Основная проблема заключалась в том, что для смены программы требовалось изменять конфигурацию электрических цепей вручную. Так как программа не сохранялась в памяти, в отличие от современных компьютеров, то для определения того, какие расчеты и в каком порядке следует произвести, требовалось подключать и отключать переключатели, как на старинных телефонных станциях. Эта задача была очень трудоемкой и требовала столько времени, что выгода от использования компьютера была крайне сомнительной.

С целью решить проблемы ENIAC были начаты работы над новым компьютером — EDVAC. Эккерт, Мокли и фон Нейман очень подробно проанализировали, как должно производиться программирование компьютера, и пришли к выводу, что оптимальным вариантом будет хранение программы в памяти подобно тому, как в ней сохранялись числа. Трудно поверить, что в прошлом компьютерные программы и аппаратное обеспечение не были разделены. Результатом этой идеи стало рождение языков программирования и программирования как отдельной дисциплины.

Создание EDVAC стало значимым событием в истории информатики.

Работы над EDVAC были закончены в 1949 году в Институте Мура Пенсильванского университета. К тому времени Эккерт и Мокли уже не участвовали в проекте, так как покинули его в 1946 году. В EDVAC использовалось 6000 ламп и 12 000 диодов, он весил 7850 килограммов и занимал площадь в 45,5 квадратных метров. Для работы ему требовалось 56 кВт электроэнергии. Он был намного легче ENIAC, учитывая масштаб этих цифр. Он также был быстрее своего предшественника: сложение выполнялось за 864 микросекунды, умножение — за 2900 микросекунд.

В это же время на «Первый черновик» фон Неймана обратили внимание в Великобритании. Морис Уилкс из Кембриджского университета в том же 1949 году сконструировал EDSAC (Electronic Delay Storage Automatic Calculator — автоматический вычислитель на электронных линиях задержки). Это была первая электронная вычислительная машина с набором внутренних команд. Однако первым компьютером с набором внутренних программ стал SSEM. Его память состояла из 512 ячеек по 17 бит каждая. Первая компьютерная игра в мире — крестики-нолики под названием ОХО — была создана на EDSAC. На основе этой вычислительной машины был создан первый компьютер, применявшийся в коммерческих целях — LEO I.

Вырезка из британской газеты, в которой рассказывается о создании EDSAC.

Оставив Пенсильванский университет, Эккерт и Мокли основали компанию Eckert-Mauchly Computer Corporation для постройки UNIVAC — акроним от Universal Automatic Computer, универсальный автоматический компьютер, где слово «универсальный» означало, что компьютер будет способен решать научные, технические, экономические и другие задачи.

Первой организацией, которая приобрела UNIVAC Эккерта и Мокли, стало Бюро переписи населения США. По завершении работ над компьютером в 1951 году компания Эккерта и Мокли была поглощена более крупной компанией Remington Rand. Второй компьютер был куплен Пентагоном в 1952 году. Эти вычислительные машины считаются первыми коммерческими компьютерами в мире.

В большинстве случаев они использовались для обработки данных, а не для физических или математических расчетов. Бюро переписи населения США использовало UNIVAC для обработки результатов переписи и формирования классификаций.

Пульт управления UNIVAC I, хранящийся в Музее науки Бостона.

Основным преимуществом UNIVAC для многих пользователей была не только скорость вычислений, но и использование лент вместо перфокарт для чтения и записи информации. Перфокарты требовали вмешательства оператора, и их замена на ленту означала увеличение степени автоматизации расчетов. Отбор данных производился самой машиной. UNIVAC производил сложение двух чисел за 0,5 микросекунды.

До выхода UNIVAC на рынок компания IBM уделяла основное внимание выпуску калькуляторов, работавших на перфокартах. Однако увидев интерес к новому компьютеру, IBM начала развивать проекты в этом направлении. Первой вычислительной машиной подобного типа стал IBM 701, который был схож с UNIVAC и назывался «электронной машиной для обработки данных». Фон Нейман, который в то время работал над созданием своего компьютера в Принстоне, участвовал в этом проекте в качестве консультанта. Работы над IBM 701 были завершены в 1952 году, а в начале 1953-го он был отправлен в лабораторию Лос-Аламоса, где велась разработка ядерного оружия.

Число ? в XX веке

Развитие аппаратного обеспечения в течение XX века позволило вычислить ? с более высокой точностью. В настоящее время известно более триллиона знаков этого числа. Последний результат содержит почти 2,7 триллиона знаков после запятой, то есть 2,7·10¹² знаков[1].

До появления компьютеров наилучших результатов добился англичанин Д. Фергюсон, который исключительно с помощью калькулятора вычислил свыше тысячи знаков: 620 знаков в 1946 году, 808 — в 1947-м, 1120 — в 1949-м (совместно с Джоном Ренчем).

Джон Ренч в том же году впервые в истории вычислил приближенное значение ? с помощью компьютера. По инициативе Джона фон Неймана расчеты производились на компьютере ENIAC. Спустя 70 часов вычислений было получено 2037 знаков Я. Пять лет спустя, в 1954 году, Николсон и Джинель превзошли этот результат, вычислив 3092 знака Я всего за 13 минут с помощью IBM NORC — самого мощного компьютера того времени. В 1959 году, опять же спустя пять лет, на IBM 704, первом массовом компьютере, где была реализована арифметика с плавающей запятой, за 4,3 часа было вычислено 16167 знаков. Расчеты произвел Франсуа Женюи в Париже. Вскоре пал рубеж в 100000 знаков: его преодолели Дэниел Шенке и Джон Ренч в 1961 году с помощью нового компьютера IBM 7090, в котором вместо электронных ламп использовались транзисторы, что позволило в шесть раз увеличить скорость расчетов по сравнению с его предшественниками. 100265 знаков были вычислены за 8,7 часа.

Джин Гийу в 1966 году установил новый рекорд, вычислив 250 000 знаков за 41 час 55 минут. Он же в 1967 году получил 500 000 знаков за 28 часов 10 минут.

Впечатляющий показатель в миллион знаков был достигнут усилиями Джина Гийу и Мартина Буйе в 1973 году. Они использовали компьютер CDC 7600 компании Control Data Corporation — конкурента IBM на рынке компьютеров второго поколения (в них использовались транзисторы), которые выпускались в 1960-е. За 23 часа 18 минут было вычислено 1001250 знаков 71.

В 1980-е главную роль играли японцы Ясумаса Канада и Казунори Миёши: в 1981 году им удалось преодолеть отметку в 2 миллиона знаков за 137 часов, в 1982-м — 8 миллионов за 6 часов 52 минуты, в 1983-м — 16 миллионов менее чем за 30 часов, в 1987-м на японском компьютере NEC SX-2 им удалось вычислить 100 миллионов знаков за 35 часов 15 минут. В 1989 году Григорий Чудновский, который считается одним из лучших среди ныне живущих математиков, и его брат Давид вычислили свыше миллиарда знаков 71 на компьютере IBM 3090.

Отметку в триллион знаков преодолел Ясумаса Канада и возглавляемая им группа, которая использовала компьютер HITACHI SR8000/MPP. Этот рекорд был установлен в Токио в декабре 2002 года. Для вычисления 1241100000000 знаков потребовалось 600 часов, то есть 25 суток вычислений, что соответствует скорости 574583 знака в секунду. В апреле 2009 года японец Дайсуке Такахаши из университета Цукуба вычислил более 2 триллионов знаков за 29,09 часа. Нынешний рекорд, который составляет почти 2,7 триллиона знаков[2], удерживает французский программист Фабрис Беллар, который использовал обычный персональный компьютер под управлением операционной системы Linux. На выполнение расчетов ему потребовался 131 день.

Большинство этих результатов были получены благодаря открытиям удивительного и загадочного индийского математика Сринивасы Рамануджана (1887–1920). Один из полученных им рядов, опубликованный в 1914 году, дает 8 новых знаков ? на каждый член ряда. Этот ряд записывается так:

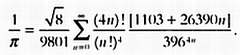
На основе результатов, полученных Рамануджаном, были найдены ряды, которые сходятся еще быстрее и позволяют получить несколько верных знаков числа ? для каждого члена ряда. Братья Джонатан и Питер Борвейн, канадцы шотландского происхождения, открыли ряд, каждый член которого дает 31 новый знак ?.

Остальные результаты, среди которых выделяются достижения Ясумасы Канады, получены с помощью формулы Карла Фридриха Гаусса (1777–1855), в которой устанавливается связь между числом ? и средним арифметико-геометрическим. Формула Гаусса записывается следующим образом:

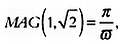
В этой формуле MAG (а, Ь) — это среднее арифметико-геометрическое чисел а и Ь.

Равенства, недавно полученные Дэвидом Бэйли, Питером Борвейном и Саймоном Плуффом, представляют собой наиболее интересные выражения, связанные с числом ?. В 1997 году эти исследователи опубликовали ряд формул, которые позволяют вычислить любой знак двоичной записи ? без необходимости вычислять предшествующие ему знаки. Эти же формулы, очевидно, можно использовать для расчета знаков ? в любой системе счисления по основанию, кратному двум, в частности в шестнадцатеричной системе счисления. Авторы подтвердили корректность своего метода, вычислив миллионный, 10-миллионный, 100-миллионный, миллиардный и 10-миллиардный знаки шестнадцатеричной записи ?. В результате были получены следующие шестнадцатеричные числа.

* * *

СРЕДНЕЕ АРИФМЕТИКО-ГЕОМЕТРИЧЕСКОЕ

Среднее арифметико-геометрическое определяется на основе двух сходящихся рядов: один из них образован средними арифметическими, другой — средними геометрическими. Напомним выражения для вычисления обеих средних величин:

МА(а, Ь) = (a + b)/2

MG(a, b) = ?(a·b).

Первые члены рядов mа и mg определяются так: ma₁ = МА(a, b), mg₁ = MG(а, b). Члены ряда в общем виде определяются так:

ma_n+1 = МА(ma_n, mg_n),

mg_n+1 = МG(ma_n, mg_n)

Эти два ряда сходятся к одному и тому же значению — среднему арифметико-геометрическому MAG(а, Ь).

* * *

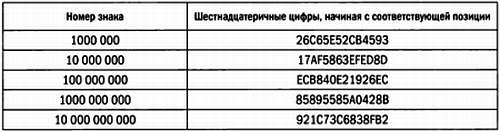
Одна из формул, предложенных Бэйли, Борвейном и Плуффом записывается так:

* * *

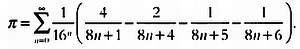
СИСТЕМЫ СЧИСЛЕНИЯ

В десятичной системе счисления, как следует из ее названия, используется десять различных цифр. Они записываются в привычном нам виде: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.

В двоичной системе счисления используются всего две цифры — 0 и 1. В шестнадцатеричной системе используется 16 цифр. Чаще всего они записываются так: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F. Символ А соответствует значению 10 в десятичной системе счисления, В — 11, С — 12, D — 13, Е — 14, F — 15.

Двоичная и шестнадцатеричная система тесно связаны между собой, так как 16 кратно 2 и перейти от одной из этих систем к другой очень просто.

Чтобы перевести число из двоичной системы в шестнадцатеричную, нужно сгруппировать биты по 4, и каждой группе будет соответствовать одна шестнадцатеричная цифра. Чтобы перевести число из шестнадцатеричной системы в двоичную, нужно заменить каждую из шестнадцатеричных цифр на четыре двоичных цифры по следующим правилам:

* * *

Сомножитель 1/16ⁿ  позволяет находить с помощью этого выражения знаки двоичной записи ?. Еще одна из предложенных ими формул выглядит так:

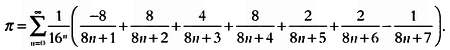
Расчеты знаков Я велись на протяжении нескольких тысяч лет, и в них участвовали наиболее выдающиеся умы в истории человечества. В настоящее время благодаря компьютерам число известных знаков ? превышает несколько триллионов, однако для большинства вычислений достаточно всего нескольких знаков.

В статье, опубликованной в специализированном журнале в 1984 году, братья Борвейн констатировали удивительный факт, не углубляясь в анализ его причин:

«На практике всего 39 знаков Я достаточно для вычисления длины окружности радиуса 2·10²⁵ метров (это расстояние больше, чем путь, который пройдет частица, движущаяся со скоростью света, в течение 20 000 миллионов лет, то есть это расстояние превышает радиус Вселенной), причем ошибка не будет превышать 10^-12 метра (это расстояние меньше радиуса атома водорода). Нет никаких сомнений, что вычисление значения ? с максимально возможной точностью имеет больше математическую, чем практическую ценность».