Глава 5 Математика в творчестве

Глава 5

Математика в творчестве

Пока что мы говорили о математическом творчестве. Но давайте посмотрим, как математика используется в областях, которые сегодня являются синонимом творчества вне рамок мира искусства, а именно в дизайне и рекламе.

Нет никаких сомнений относительно того, какую роль играла и продолжает играть геометрия в дизайне. Она неизбежно применяется при создании чего-то материального и осязаемого. С начала XX века чисто геометрические фигуры используются в дизайне самых разных товаров, особенно в дизайне мебели и упаковки. Дизайнеры, обладающие эстетическим вкусом, стремящиеся к абстракции и экономии форм, с помощью геометрических фигур делают свои работы более элегантными.

Используется математика и в мире рекламы. В последние десятилетия растущий интерес к науке вдохновил авторов рекламных кампаний на использование различных математических инструментов, чтобы повысить доверие к рекламируемому товару. Графики, формулы, геометрические фигуры, символы, числа и расчеты стали все чаще встречаться во всех средствах массовой информации, как печатных, так и аудиовизуальных.

Математика играет важную роль в дизайне и рекламе по двум причинам. С одной стороны, тот факт, что и дизайнеры, и специалисты по рекламе грамотно используют математические идеи, расширяет область применения этих идей. С другой стороны, когда математические понятия появляются в контекстах, не связанных с миром науки и технологий, они помогают по-новому понять знакомые нам идеи, делая их еще более доступными.

Можно привести множество примеров применения математических идей в сфере дизайна или рекламы. Проанализируем некоторые из них.

Математика в рекламных стратегиях

Тенденциозное использование пропорций

Непрерывная борьба за аудиторию приводит к тому, что теле- и радиокомпании в своей рекламе преувеличивают свои достижения и преуменьшают результаты конкурентов. Типичным примером является демонстрация графиков для того, чтобы сделать рекламу убедительнее. Чтобы подчеркнуть преимущество телеканала А над телеканалом В по охвату аудитории, обычно используются графики, подобные следующему:

Допустим, что приведенные на графике данные верны, и телеканал А действительно популярнее телеканала В. Тем не менее разница в размерах между столбцами диаграммы значительно преувеличивает это преимущество. Прямоугольник, обозначающий аудиторию канала А, намного больше, чем прямоугольник, обозначающий аудиторию канала В:

А: 29,6 — 27,5 = 2,1;

В: 28,8 — 27,5 = 1,3 => А/В = 2,1/1,3 = 1,615.

В действительности разница между аудиториями каналов составляет восемь десятых процента, поэтому высота одного прямоугольника должна быть менее чем на 2,8 % больше высоты другого. Корректнее было бы изобразить прямоугольники во всю длину:

Если мы будем обрезать эти прямоугольники произвольным образом, то кажущееся соотношение их размеров может увеличиться до бесконечности. Оно будет тем больше, чем ближе к краю прямоугольника В пройдет линия отреза.

Реальную разницу можно очень сильно преувеличить и даже сделать ее сколь угодно большой:

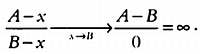
Похожая проблема связана и с графиками, иллюстрирующими колебания курсов валют. Изменение курса валют в течение недели может показаться незначительным или огромным в зависимости от выбранного масштаба вертикальной оси графика:

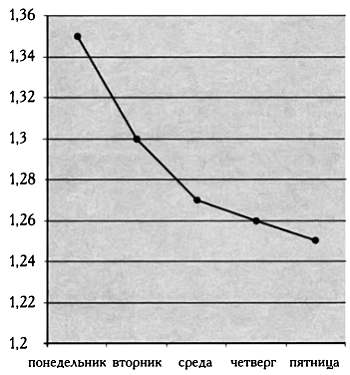
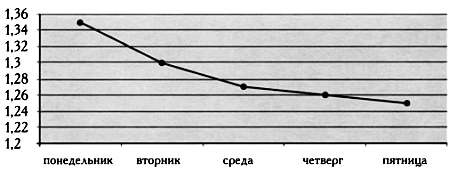
Стремление проиллюстрировать на графиках отношение величин или их разницу очень часто встречается в рекламе, но, к сожалению, результат оказывается прямо противоположным: точность графиков является мнимой. Числа и графики обладают строгостью, присущей математике, но только при объективном использовании.

Вероятность

Несколько лет назад в рекламе одной телефонной компании прозвучала фраза: «Вероятность того, что сын вашего начальника и вы — это один и тот же человек, равна 0,00000000001 %».

В математике вероятность — это численная характеристика возможности возникновения какого-либо события. Классическое определение вероятности звучит как отношение числа благоприятных исходов к общему числу возможных исходов.

Например, вероятность того, что при броске шестигранного кубика выпадет число очков x, меньшее 3, равна 2/6, так как число благоприятных исходов равно 2 (выпадет одно либо два очка), общее число исходов — 6:

Р(х < 3) = 2/6 = 1/3 = 0,333…

Чтобы рассчитать вероятность того, что некий человек — сын своего начальника, нужно найти отношение числа благоприятных исходов к общему числу возможных исходов. Так как у любого человека может быть только один отец, число благоприятных исходов в этом случае равно единице. Чтобы определить число возможных исходов, нужно узнать, сколько всего начальников в мире, что практически невозможно. Из общего числа жителей Земли, превышающего шесть миллиардов человек, нужно исключить женщин (речь идет о начальнике, а не о начальнице), бездетных, безработных и тех, кто не занимает руководящую должность. Тогда число возможных исходов будет меньше половины от шести миллиардов. Таким образом, вероятность будет равна:

P ~= (1/3·10⁹) = 3,33·10^-10.

Вероятность, указанная в рекламном слогане, равна:

Q = (0,00000000001/100) = 10^-13

Это предполагает существование 10¹³ начальников и численность населения Земли, равную 2·10¹³  человек, а это в 600 раз больше реального населения Земли:

P/Q = 3,33·10^-10/2·10^-13 = 600

Нам неизвестно, почему автор рекламного слогана выбрал именно число 0,00000000001 %, однако ему, несомненно, удалось показать, что ни один человек на планете не является сыном своего начальника. Чем больше нулей после запятой в записи десятичной дроби, тем меньше значение этой дроби. Если приписать к этому числу знак %, оно уменьшится еще в сто раз.

Перед нами — пример творчества, в котором невозможность события подчеркивается с помощью очень малой величины. Хотя 0 % описывает вероятность абсолютно невозможного события, визуальный эффект от числа 0,00000000001 % выше, поэтому автор его и использовал.

Необычная алгебра

Порой реклама автомобилей представляет собой настоящий полет творческой мысли. В последние годы все чаще основной упор делается на технологии, геометрию и математику. Это особенно заметно в рекламе дорогих автомобилей.

В одной рекламной кампании, запущенной несколько лет назад, был показан автомобиль, отражавшийся в идеально зеркальной поверхности пола. В результате казалось, что автомобиль словно парит над зеркалом. Над изображением автомобиля можно было прочесть формулу и слоган:

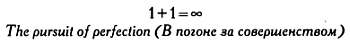
Имеет ли какое-то отношение равенство 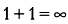 к стремлению к совершенству?

Сначала может показаться, что приравнять к бесконечности сумму двух конечных чисел, какими являются единицы, нельзя, поскольку неожиданно получается:

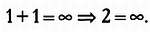
Быть может, это равенство имеет какой-то смысл? Пусть в повседневной трактовке бесконечности и в привычной трактовке суммы чисел это не так, однако существуют и другие трактовки, в которых это равенство может быть абсолютно верным.

Будем рассматривать не множество натуральных чисел в целом, а множество X, содержащее всего три элемента:

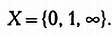
Сопоставим элемент 0 с нулем, элемент 1 — с произвольной конечной величиной, элемент ©о — с некоторой величиной, которая не является ни нулевой, ни конечной. С учетом вышесказанного логично предполагать, что

Ничто + что-то = что-то.

Конечное + конечное = конечное.

Бесконечность + что-то = бесконечность.

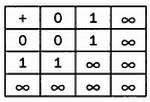
Поэтому сумма 1 + 1 должна быть не бесконечной, а конечной, а операция сложения на множестве X должна описываться следующей таблицей:

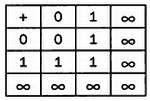
Эта операция сложения обладает привычными нам свойствами. Так, она коммутативна (описывающая ее таблица симметрична относительно диагонали), содержит нейтральный элемент (ноль), который при сложении с любым другим элементом оставляет его неизменным, кроме того, эта операция обладает ассоциативностью (порядок сложения трех элементов не влияет на итоговый результат). Сохранятся ли эти свойства, если мы заменим равенство 1 + 1 = 1 на  , как указано в рекламном слогане? Иными словами,

В этом случае таблица по-прежнему симметрична относительно диагонали. Ноль по-прежнему является нейтральным элементом. Свойство ассоциативности также сохраняется.

Однако не выполняется одно из ожидаемых свойств — ни для 1, ни для 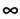 нет противоположного элемента. Не существует элемента, который в сумме с 1 давал бы 0, и не существует элемента, который в сумме с  давал бы 0. Чтобы исправить это, необходимо, чтобы в каждой строке или в каждом столбце таблицы имелся минимум один 0. Очевидно, что если заполнить таблицу нулями, проблема будет решена, однако подобное решение нас не устраивает.

Цифры в первой строке и в первом столбце таблицы неоспоримы, так как при сложении нуля с любой величиной результатом всегда является эта величина. Если мы определим  , новая таблица примет вид:

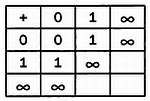
Чтобы для операции сложения были определены противоположные элементы, 0 должен встречаться в каждой строке и в каждом столбце. Если мы хотим, чтобы эта операция обладала коммутативностью, таблица должна быть симметричной относительно диагонали. Обеспечить это можно всего несколькими способами:

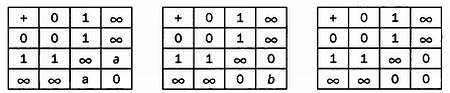
Не существует значения а такого, чтобы операция сложения, определенная в первой таблице, обладала бы ассоциативностью:

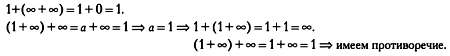
Третья таблица также не подходит:

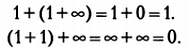
Только подставив b = 1 во вторую таблицу, мы получим верное решение. Конечно, равенства 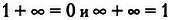противоречат нашим привычным представлениям.

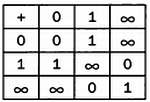
Мы создали алгебраическую структуру, состоящую из множества X = {0, 1, } и операции +, обладающей требуемыми свойствами, результаты которой всегда принадлежат множеству X. Результаты операции сложения для элементов множества X непривычны для нас, но это тема отдельного разговора.

Линейные и экспоненциальные функции

На упаковках губок одной марки в течение нескольких лет приводился график с текстом: «Не позволяйте бактериям размножаться». На нем были изображены две стрелки в координатной плоскости. Одна иллюстрировала результаты применения губки, другая — скорость размножения бактерий без использования губки.

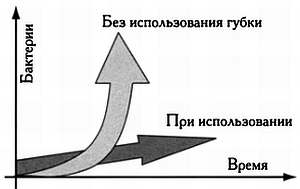
Заслуживает внимания правильное использование терминологии и графика.

Численность бактерий с течением времени возрастает. В рекламном тексте говорится, что при использовании губки численность бактерий перестанет умножаться. Допустим, в единицу времени появляется b новых бактерий, при этом b > 1. По прошествии t единиц времени их число будет равно:

B(t) = Ь·Ь·Ь… ^{(t раз)}…·Ь = b^t.

Это показательная функция с основанием степени b, графиком ее является восходящая кривая, наклон которой постепенно растет, и на бесконечности график обращается в вертикальную линию.

Если численность бактерий будет не умножаться, а складываться, то их численность по прошествии t единиц времени будет описываться формулой:

B(t) = Ь + Ь + Ь… ^{(t раз)}… + Ь = b·t.

Это линейная возрастающая функция, наклон которой постоянен (тангенс угла наклона графика равен Ь) и графиком которой является прямая. За исключением того, что начальная точка графиков показательных функций обычно не совпадает с началом координат, на упаковке воспроизведены графики обеих функций. С точки зрения математики они абсолютно верны, так как график показательной функции соответствует случаю, когда численность бактерий умножается.

Правило третей

При создании изображений работает правило, согласно которому деление на трети важнее деления на половины. Желательно не располагать основные элементы композиции точно в центре.

Например, горизонт на фотографии лучше расположить выше или ниже линии, делящей прямоугольный кадр пополам.

Если на фотографии присутствует два важных элемента, лучше расположить их в точках пересечения линий, делящих кадр на три части по горизонтали и по вертикали. В этом случае геометрическое правило помогает создать гармоничную композицию.

Как математика помогает достичь совершенства

Некоторое время назад один из производителей вина запустил рекламную кампанию, смысл которой сводился к тому, что совершенство его продукции обусловлено сочетанием математики, природы и мастерства. В рекламном ролике показывался длиннейший ряд математических формул, большинство из которых не несли особого смысла, а многие цифры и буквы в них были заменены изображениями природы или фотографиями мастеров-виноделов. Ряд формул заканчивался знаком равенства, по другую сторону которого была изображена бутылка вина. Рядом с бутылкой располагался слоган: «Кто сделал его совершенным?».

Замысел автора рекламы заключался в том, чтобы с помощью математических инструментов показать, сколь длительным и скрупулезным является процесс изготовления вина, ведь именно слова «длительность» и «скрупулезность» описывают большую часть математической деятельности.

Математика в дизайне

Двоичное время

В двоичной системе счисления для представления любых чисел используются всего две цифры — 0 и 1. Подобно десятичной системе счисления, каждый разряд числа в двоичной системе соответствует определенной степени двойки:

372₁₀ =3·10² + 7·10¹ + 2·10⁰;

101₂ =1·2² + 0·2¹ + 1·2⁰.

В таблице ниже представлены тринадцать первых натуральных чисел в обеих системах счисления:

Дизайнеры порой удивляют нас неожиданными решениями. Мы привыкли измерять время в часах, которые делятся на 60 минут, и в минутах, которые делятся на 60 секунд. Часы, показывающие время в двоичной системе счисления, поначалу могут показаться экстравагантной выдумкой. Их циферблат представляет собой прямоугольник. На верхней линии обозначаются часы, на нижней — минуты.

Внутри прямоугольника находятся четыре вертикальные линии, на которых указываются значения, соответствующие каждой степени двойки (см. рисунок ниже). Так как число часов находится в интервале от 0 до 12, для представления часов достаточно четырех цифр (см. таблицу на предыдущей странице). Для обозначения минут, число которых находится на интервале от 0 до 60, требуется шесть цифр.

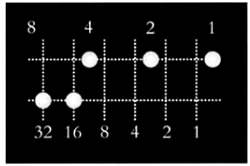
Взглянув на эти часы, сразу узнать время нельзя — сначала нужно сложить значения, отмеченные на каждой линии. Часы на рисунке выше показывают 7 часов и 48 минут. Четверть часа, полчаса и три четверти часа обозначаются так:

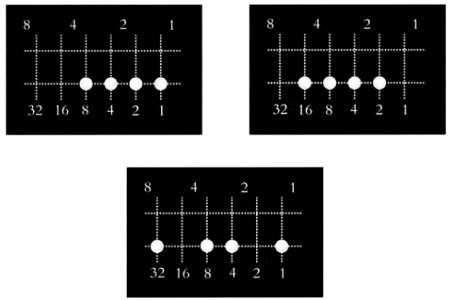
Сначала эти часы кажутся неудобными, но постепенно по ним можно научиться определять время так же быстро, как и по обычным. Эти часы — удивительный пример того, как математика стала основой дизайна вещи.

Лента Мёбиуса

Если соединить противоположные стороны прямоугольной ленты ABCD, то есть совместить пары вершин АС и BD, получится кольцо. На следующем рисунке стрелкой показано, как именно совмещаются вершины исходного прямоугольника:

А чтобы построить ленту Мёбиуса, необходимо соединить вершину А с вершиной D, В — с С:

В результате получается кольцо, у которого всего одна граница и одна сторона.

Эта необычная геометрическая фигура используется в дизайне ювелирных украшений, в частности колец. Реклама этих колец сопровождается текстами, которые подчеркивают их особенности.

— Особые топологические свойства: «Это чудесное серебряное кольцо имеет уникальную форму: у него всего одна сторона. Его форма символизирует равновесие между внутренним и внешним я.

— Свойства, которые можно считать следствием особой формы кольца: «Как маленькая золотая лента может заставить вас почувствовать, что весь мир вращается у вас вокруг пальца? Оно совершенно…»

Обычные кольца имеют цилиндрическую форму и две стороны — внешнюю и внутреннюю. С пальцем соприкасается только внутренняя сторона. Если внутренняя сторона соприкасается с пальцем, то внешняя — со всем остальным, то есть с целым миром. Кольцо Мёбиуса имеет всего одну сторону. Следовательно, та сторона кольца, которая соприкасается с пальцем, соприкасается и со всем остальным миром. Нет различий между «внутри» и «вне», поэтому действительно можно сказать, что с кольцом Мёбиуса весь мир будет вращаться вокруг вашего пальца. В этом случае речь идет не просто о математическом объекте, взятом за основу дизайна, — также были созданы корректные и непротиворечивые трактовки, помогающие понять его математические свойства.

* * *

ГЕКСАМИНО И ДИЗАЙН

На рисунке ниже изображена развертка картонной коробки, в которую укладываются шапочки для душа в гостиницах. Эта развертка называется гексамино, так как состоит из шести одинаковых фигур, или модулей, соединенных сторонами.

Посредством последовательных сгибов из этой развертки получается трехмерный многогранник — гексаэдр, то есть куб. Существует одиннадцать различных гексамино, из которых можно сложить куб.

* * *

Дух геометрии

В дизайне парфюмерных флаконов иногда используются настоящие геометрические головоломки с алгебраическими формулами. Так произошло с мужским одеколоном и дезодорантом известной японской марки. Дизайнер создал два флакона разной формы, которые, сложенные вместе, образовывали квадрат. Один из флаконов имел форму квадрата, другой представлял собой симметричную фигуру:

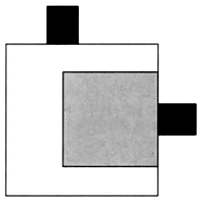
Вместимость большого флакона равнялась 75 мл, малого — 50 мл. В рекламе основной упор делался на суммарном объеме флаконов и их особой форме:

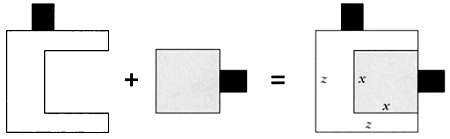
Сможете ли вы определить реальные размеры флаконов? Объем меньшего равен 50 мл, большего — 75 мл. Суммарный объем флаконов равен 125 мл. Так как флаконы идеально укладываются друг в друга, их толщина одинакова, следовательно их объемы пропорциональны площадям видимых поверхностей. Учитывая, что 1 мл воды эквивалентен 1 см³, можно вполне обоснованно считать, что сторона х малого флакона и сторона z большого флакона соответственно равны:

50 = x² => х = ?50 = 7,1 см;

125 = z² => z = ?125 ~= 11,2 см.

Почему пазлы из 2000 элементов не содержат ровно 2000 элементов

Не всегда можно создать предметы точно такой формы или из точно такого числа элементов, как этого хочется их автору. Многие из вас наверняка собирали головоломки-пазлы, но немногие подсчитывали точное число их элементов. Некоторые могут возразить, что подобный подсчет не нужен, так как число элементов всегда указано на коробке: 500, 1000, 2000, 3000, 5000, 8000. Однако изготовители головоломок обманывают нас или, по меньшей мере, не говорят всей правды.

Пазлы из 500 элементов действительно содержат 500 элементов, но пазлы из 2000 элементов не содержат 2000 элементов, и чтобы убедиться в этом, не требуется подсчитывать их все. Все пазлы образуют форму прямоугольника, их элементы имеют различную форму, однако вырезаются из прямоугольного основания, в котором проделываются выступы и выемки. При изготовлении пазла из 2000 элементов нужно найти два целых числа, обозначающих число элементов на каждой стороне прямоугольника, произведение которых будет равно 2000. Так как 2000 = 24· 53, возможны следующие варианты:

1·2000 = 2·1000 = 4·500 = 8·250 = 10·200 = 16·125 = 20·100 = 25·80 = 40·50.

Соотношение ширины и высоты собранного пазла должно быть гармоничным и приближаться к соотношению сторон листа стандартного формата А4, то есть примерно равно 1,4. Однако прямоугольники, длины сторон которых являются делителями числа 2000, будут либо слишком вытянутыми, либо слишком «квадратными»:

50/40 = 1,25

80/25 = 3,2

Поэтому вместо 2000 используется 1998 элементов: разложив 1998 на простые множители, мы увидим, что два его делителя описывают прямоугольник, соотношение сторон которого очень близко к желаемому:

1998 = 2·3³·37 => (2·3³/37) = 54/37 ~= 1,46

Это интересный пример того, как разложение натурального числа на простые множители определяет дизайн предмета.

Снятие макияжа и теорема Пифагора

Макияж обычно снимают с лица специальными небольшими салфетками. Каждый производитель изготавливает салфетки особой формы, порой весьма далекой от привычных квадратов, прямоугольников или кругов.

На следующем рисунке изображен дизайн губки для снятия макияжа. На иллюстрации представлен вид сверху, но не следует забывать, что губка является трехмерной и имеет толщину, равную примерно двум сантиметрам. Она состоит из четырех частей, которые складываются подобно элементам головоломки:

Именно эта головоломка используется в одном из самых понятных доказательств теоремы Пифагора. Пусть а — сторона квадрата (гипотенуза каждой из маленьких салфеток), b и с — стороны салфеток, перпендикулярные друг другу (катеты).

В этом случае площадь большого квадрата выражается так:

a² = 4·(b·c/2) + (b — c)²

a² = 2bx + b² — 2bc + c²

a² = b² + c²

Темы с вариациями

Композиторы знают, что один и тот же мотив, повторяясь, задает основную тему произведения, однако если тема повторяется без изменений, мелодия может оказаться монотонной и скучной. Красота хорошей музыкальной композиции проявляется не столько в самом мотиве, сколько в том, насколько разнообразны его вариации.

Дизайнеры верны этой идее, повторяя бесконечное множество раз логотип в дизайне товаров и упаковок. В подобных случаях чаще всего используется симметрия, которая не изменяет форму фигуры, а варьирует лишь ее местоположение.

Существует три преобразования на плоскости, которые сохраняют неизменными форму и размер: перенос, поворот и осевая симметрия (отражение).

Перенос изменяет местоположение, при повороте фигура вращается относительно неподвижной точки, называемой центром вращения, отражение, или осевая симметрия, заменяет исходную фигуру ее зеркальным отражением. С помощью этих трех преобразований один и тот же мотив может повторяться множеством способов, и всего существует семнадцать узоров, принципиально различных с математической точки зрения. В дизайне не требуется столько разных узоров — например, для логотипа в форме буквы Z используются только узоры, изображенные на рисунке ниже. Можно заметить, как повторяющаяся буква теряет исходный смысл и превращается в условный символ, служащий основой орнамента.

Преимущество подобного дизайна заключается в том, что марка становится узнаваемой, а паттерн легко воспроизвести автоматически, так что эту идею используют в своей продукции очень многие производители.