Глава 2 Хотите ли вы знать число π?

Порой в «Симпсонах» упоминаются малоизвестные математические концепции, и с некоторыми из них мы действительно встретимся в следующей главе. Однако в остальных случаях шуточные ситуации, смоделированные Рейссом, Джином и их коллегами в эпизодах сериала, касаются хорошо знакомых многим зрителям математических концепций. Классический пример – число ?, неоднократно появлявшееся в мультсериале за прошедших два десятилетия.

На всякий случай напоминаю, что ? – это отношение длины окружности к ее диаметру. Для того чтобы составить представление о приблизительном значении числа ?, можно нарисовать окружность, а затем отрезать кусок веревки длиной, равной ее диаметру. Если проложить этот кусок веревки по краю окружности, он поместится там немногим более трех раз – точнее говоря, 3,14 раза. Это и есть приблизительное значение числа ?. Соотношение между числом ?, длиной окружности и диаметром можно описать с помощью следующего уравнения:

длина окружности = ? ? диаметр

C = ?d

Поскольку диаметр окружности в два раза больше радиуса, это уравнение можно записать в таком виде:

длина окружности= 2 ? ? ? радиус

C = 2?r

Пожалуй, это и есть первый маленький шаг, который мы совершаем в детстве при переходе от простой арифметики к более сложным концепциям. Я до сих пор помню свою первую встречу с числом ?, настолько она тогда меня потрясла. Математика больше не сводилась исключительно к умножению в столбик и простым дробям; теперь в ней появилось нечто таинственное, элегантное и универсальное: каждый круг в этом мире подчиняется уравнению с участием числа ?, от колеса обозрения до фрисби, от лепешки до земного экватора.

Кроме того, помимо вычисления длины окружности, число ? можно использовать для расчета площади, которая ограничена этой окружностью:

площадь = ? ? радиус?

A = ?r?

В эпизоде «Человек-пирог» (Simple Simpson, сезон 15, эпизод 19; 2004 год) есть основанная на игре слов шутка, касающаяся приведенного выше уравнения. В этом эпизоде Гомер изображает супергероя по имени Человек-пирог, который наказывает злодеев, бросая им в лицо пирог. И первый его акт возмездия в данном качестве направлен на обидчика Лизы. Свидетелем сцены становится персонаж по имени Дредерик Тейтум, знаменитый бывший боксер из Спрингфилда, который заявляет: «Все мы знаем формулу ?r?, но сегодня мы говорим: “Пирог – это справедливость”. Я приветствую это».

И хотя шутку включил в сценарий Эл Джин, он неохотно приписывает себе эту заслугу (или, возможно, вину): «Да это же очень старая шутка. Я услышал ее много лет назад. Человек, которого следует поблагодарить за нее, – кто-то из 1820 года».

Джин явно преувеличивает, когда упоминает 1820 год, но слова Тейтума действительно представляют собой новую интерпретацию классической шутки, передаваемой из поколения математиков в поколение. Самая известная ее версия появилась в 1951 году в американском комедийном сериале The George Burns and Gracie Allen Show («Шоу Джорджа Бернса и Грейси Аллен»). В эпизоде под названием «Как девушка-подросток проводит уик-энд» Грейси приходит на помощь юной Эмили, которая жалуется на домашнее задание:

Эмили. Хотелось бы мне, чтобы геометрия была такой же легкой, как испанский язык.

Грейси. Так, может, я тебе помогу? Скажи мне что-нибудь на языке геометрии.

Эмили. Сказать что-нибудь на языке геометрии?

Грейси. Да, давай же.

Эмили. Ну хорошо. Ммм… ?r?.

Грейси. И этому учат сейчас в школе? ?r??

Эмили. Да.

Грейси. Эмили, пирог круглый. Печенье круглое. Крекеры квадратные.

В основе этой шутки лежит похожее звучание слова pie («пирог») и названия буквы ?, что и служит поводом для каламбура. Следовательно, комики должны быть благодарны Уильяму Джонсу за введение символа ?. Этот математик XVIII столетия, так же как и многие другие ученые, зарабатывал себе на жизнь уроками в лондонских кофейнях, посетители которых должны были заплатить за вход один пенни. Преподавая в этих так называемых грошовых университетах, Джонс параллельно работал над крупным научным трудом под названием A New Introduction to the Mathematics («Новое введение в математику»). Именно в этой книге он впервые использовал греческую букву ? в контексте обсуждения геометрии круга. В итоге появилась почва для новых математических каламбуров. Джонс выбрал символ ?, потому что это начальная буква греческого слова ????????? (периферия), что означает «окружность».

* * *

За три года до появления шутки с числом ? в эпизоде «Человек-пирог» авторы «Симпсонов» уже упоминали это число в серии «Пока, пока, зубрила» (Bye, Bye, Nerdie, сезон 12, эпизод 16; 2001 год). Но на этот раз вместо воскрешения старой шутки сценаристы создали совершенно новую, хотя и основанную на одном любопытном случае из истории числа ?. Для того чтобы оценить ее по достоинству, сперва необходимо вспомнить значение числа ? и то, как оно измерялось на протяжении столетий.

Я уже говорил, что ? = 3,14 – всего лишь приближенное значение. Дело в том, что ? – иррациональное число, то есть назвать его абсолютно точное значение невозможно, поскольку в нем бесконечное количество десятичных знаков, в которых отсутствует какая-либо закономерность. Тем не менее математики прошлого ставили перед собой задачу выйти за рамки существующей приближенной оценки 3,14 и поймать это ускользающее число, рассчитав его максимально точное значение.

Первую серьезную попытку это сделать предпринял Архимед в третьем столетии до нашей эры. Он понимал, что точность измерения ? зависит от точности измерения длины окружности. Но это весьма сложная задача, так как окружность состоит из кривых малой кривизны, а не из прямых линий. Важным достижением Архимеда стало решение обойти проблему измерения кривых путем аппроксимации окружности прямыми линиями.

Возьмем окружность, диаметр которой (d) равен единице. Мы знаем, что C = ?d, а значит, длина окружности (С) равна ?. Затем нарисуем два квадрата, один за пределами окружности и один внутри нее.

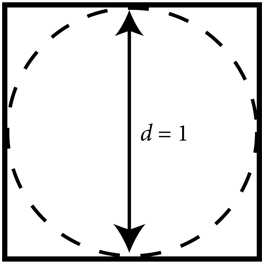
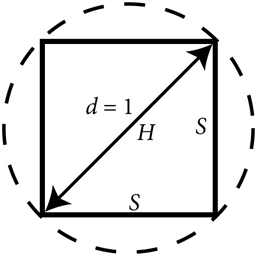
Безусловно, настоящая окружность должна быть меньше периметра большего квадрата и больше периметра меньшего квадрата. Таким образом, измерив периметры двух квадратов, мы получим верхний и нижний пределы длины окружности.

Периметр большего квадрата измеряется легко, поскольку каждая его сторона имеет ту же длину, что и диаметр круга, который, как нам известно, равен единице. Следовательно, периметр большего квадрата составляет 4 ? 1 = 4 единицы.

Периметр меньшего квадрата вычислить несколько труднее, но мы можем определить длину каждой его стороны с помощью теоремы Пифагора. Очень кстати, что диагональ квадрата и две его стороны образуют прямоугольный треугольник, гипотенуза (H) которого не только совпадает с диагональю квадрата, но и имеет ту же длину, что и диаметр окружности, то есть единицу. Теорема Пифагора гласит, что квадрат гипотенузы равен сумме квадратов его катетов. Если мы обозначим их символом S, то H? = S? + S?. Если H = 1, то две другие стороны должны иметь длину 1/?2 единиц. Следовательно, периметр меньшего квадрата равен 4 ? 1/?2 = 2,83 единицы.

Учитывая, что длина окружности должна быть меньше периметра большого круга и больше периметра малого, мы можем с уверенностью заявить, что она должна попадать в промежуток от 2,83 до 4,00.

Не забывайте: ранее мы утверждали, что длина окружности диаметром 1 единица равна ?, поэтому значение ? должно находиться между 2,83 и 4,00.

В этом и состояло великое открытие Архимеда.

Возможно, оно не произвело на вас особого впечатления, ведь мы уже знаем, что ? равно примерно 3,14, так что нижний предел 2,83 и верхний – 4,00 не представляют для нас никакого интереса. Однако сила открытия Архимеда состояла в том, что его результат подлежал уточнению. Вместо того чтобы размещать окружность между большим и малым квадратами, Архимед разместил ее между большим и малым шестиугольниками. Если у вас есть десять свободных минут и вы уверенно оперируете числами, то можете попробовать сами доказать, что по результатам измерения периметра этих двух шестиугольников значение числа ? должно быть больше 3,00 и меньше 3,464.

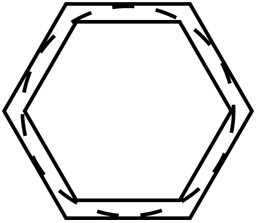
У шестиугольника больше сторон, чем у квадрата, что делает его более точным приближением к окружности. Это объясняет, почему шестиугольник позволяет вычислить более узкие пределы для значения ?. Тем не менее и в этом случае имеет место значительная погрешность. Поэтому Архимед продолжал расчеты, применяя этот метод снова и снова и увеличивая количество сторон многоугольника, благодаря чему получал все более точное приближение к окружности.

В конечном итоге упорство привело Архимеда к тому, что он заключил окружность между двумя многоугольниками с 96 сторонами и рассчитал периметр обеих фигур. Это было впечатляющее достижение, особенно учитывая, что Архимед не имел современной алгебраической системы обозначений, ничего не знал об арифметических действиях с десятичными дробями и ему приходилось выполнять все эти громоздкие вычисления вручную. Однако работа стоила затраченных усилий, поскольку ему удалось заключить значение числа ? между числами 3,141 и 3,143.

Через восемь столетий, в V веке нашей эры, китайский математик Цзу Чунчжи развил подход Архимеда на шаг дальше (или на 12 192 шага, если точнее), использовав два многоугольника с 12 288 сторонами для доказательства того, что значение числа ? лежит между числами 3,1415926 и 3,1415927.

По всей вероятности, к этому моменту вы уже поняли, что определение значения числа ? – непростая задача, работа над которой будет продолжаться вечно, а все потому, что ? – иррациональное число. Но есть ли смысл в вычислении значения ? с более высокой точностью? Мы вернемся к этому вопросу чуть позже, а пока вы уже узнали о числе ? достаточно для того, чтобы перейти к контексту математической шутки из эпизода «Пока, пока, зубрила».

Сюжет этого эпизода сфокусирован на травле умников, которая по-прежнему остается глобальной проблемой, несмотря на мудрые слова американского педагога Чарльза Сайкса, написанные в 1995 году: «Будь вежлив с ботаниками. Не исключено, что однажды ты будешь работать на одного из них». Когда Лиза задается целью найти объяснение того, почему хулиганы так любят нападать на умников, ей приходит в голову мысль, что они издают запах, который отмечает их как жертв. Лиза убеждает нескольких школьных друзей из числа ботанов поработать на спортивных тренажерах до пота, а затем собирает его и анализирует. После длительных исследований ей наконец удается выделить феромон, который источает каждый «умник, ботаник и очкарик» и который, возможно, притягивает хулиганов. Лиза называет его «пойндекстрозой»[8], в честь вундеркинда Пойндекстера, персонажа мультсериала 1959 года Felix the Cat («Кот Феликс»).

Для того чтобы проверить свою гипотезу, Лиза наносит немного пойндекстрозы на пиджак грозного бывшего боксера Дредерика Тейтума, пришедшего в ее школу. Как и следовало ожидать, феромон притягивает школьного хулигана Нельсона Манца. И хотя Нельсон понимает, что нападать на бывшего боксера абсолютно бессмысленно, он не может сопротивляться воздействию пойндекстрозы и даже вытягивает у Тейтума трусы.

Взволнованная своим открытием, Лиза решает представить отчет о работе «Воздушные феромоны и агрессия хулиганов» на конференции «12-я ежегодная научная штука», которую ведет любимец обитателей Спрингфилда, рассеянный профессор Джон Нерделбаум Фринк-младший. Фринк пытается представить Лизу, но атмосфера на конференции настолько накалена, а ее участники так возбуждены, что ему трудно призвать их к порядку. В конце концов Фринк в отчаянии восклицает: «Ученые, ученые! Прошу, прошу порядка! К порядку, смотреть вперед, руки сложить, слушать внимательно. Число ? равно трем!»

Шум внезапно прекращается. Идея профессора Фринка сработала, поскольку он совершенно правильно предположил, что заявление о точном значении числа ? так поразит присутствующих в зале, что они потеряют дар речи. Как смеет кто бы то ни было заменять тройкой число 3,141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513… после тысячелетних попыток определить его значение с невероятной точностью!

Эта сцена перекликается с лимериком, написанным историком, профессором колледжа Колорадо Харви Картером (1904–1994):

Tis a favorite project of mine,

A new value of pi to assign.

I would fix it at 3

For it’s simpler, you see,

Than 3 point 1 4 1 5 9.

(Люблю я это делать –

Искать новое значение «пи».

Я бы выбрал число 3.

Как видите, оно попроще,

Чем 3 запятая 1 4 1 5 9.)

Однако возмутительное заявление профессора Фринка основывалось не на странном лимерике Картера. Эл Джин рассказал о том, что он предложил фразу «Число ? равно трем!», поскольку незадолго до этого прочитал об инциденте, имевшем место в штате Индиана в 1897 году, когда политики попытались закрепить официальное (и совершенно неправильное) значение ? на законодательном уровне.

Законопроект о числе ? (официальное название – «Законопроект № 246»), принятый в нижней палате штата Индиана, был детищем Эдвина Гудвина, врача из города Солитьюд, расположенного в юго-западной части штата. Гудвин обратился к законодательному собранию штата с предложением принять закон, в основу которого было положено его решение задачи, известной как «квадратура круга» (древняя задача, не имеющая решения, что было доказано в 1882 году). Сложные и противоречивые объяснения Гудвина содержали следующую строку, касающуюся диаметра круга:

…Четвертый важный факт состоит в том, что отношение диаметра к окружности равно пяти четвертым к четырем.

Отношение длины окружности к диаметру равно числу ?, а значит, Гудвин, по сути, предлагал определять значение ? по следующей формуле:

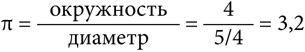
Гудвин заявил, что школы штата Индиана могут использовать его открытие бесплатно, но власти штата разделят с ним прибыль от роялти, взимаемого с других школ, которые захотят принять значение числа ? равным 3,2. Поначалу специальный характер законопроекта озадачил политиков, которые передали его на рассмотрение из палаты представителей в финансовый комитет, затем в комитет по болотам и в конце концов в комитет по вопросам образования, где из-за неразберихи его приняли без возражений.

Далее законопроект должен был одобрить сенат штата. К счастью, некий профессор Уолдо, возглавлявший в то время факультет математики Университета Пердью в городе Уэст-Лафейетт, отправился в тот день в здание законодательного собрания для обсуждения финансирования Академии наук штата Индиана. По случайному стечению обстоятельств один из членов финансового комитета показал законопроект профессору и предложил познакомить его с доктором Гудвином. Однако Уолдо ответил, что в этом нет необходимости, поскольку он и без того знает немало чокнутых.

Профессор Уолдо сделал все для того, чтобы сенаторы поняли абсурдность законопроекта Гудвина и высмеяли его, и таки добился своего. В Indianapolis Journal была опубликована следующая цитата сенатора Оррина Хаббелла: «С таким же успехом сенат может принять закон о том, чтобы вода текла под гору, и законодательно устанавливать математические истины». В конечном итоге принятие законопроекта отложили на неопределенный срок.

Нелепое заявление профессора Фринка о том, что ? равно 3, – искусное напоминание о том, что законопроект Гудвина до сих пор лежит где-то в ящике для бумаг в подвале здания законодательного собрания штата Индиана и ждет, когда какой-либо болван вернет его к жизни.