Приложение 5 Теорема Килера

В эпизоде «Узник Бенды» Милейший Клайд Диксон пишет доказательство теоремы Килера (также известной как теорема Футурамы) на флуоресцентной зеленой доске. Вот расшифровка этого доказательства.

Во-первых, пусть ? представляет собой k-циклическую перестановку на множестве [n] = {1, …, n}. Без потери общности запишем:

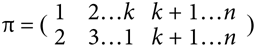
Пусть <a, b> означает перестановку, которая обеспечивает обмен содержимого a и b.

Согласно предположению, ? образуется посредством k отдельных перестановок на множестве [n].

Введем два новых элемента и запишем:

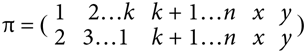
Для любого i = 1, …, k пусть ? представляет собой серию перестановок «слева-направо»:

? = (< x, 1> < x, 2> … < x, i>) (< y, i + 1> < y, i + 2> … < y, k>) (< x, i + 1>) (< y, 1>)

Обратите внимание, что каждая перестановка приводит к обмену элемента из [n] на один из элементов {x, y}, а значит, все они отличны от перестановок в пределах множества [n], которые привели к образованию ?, а также от <x, y>. Обычная проверка показывает, что теперь:

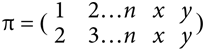
Другими словами, ? возвращает k-цикл в прежнее состояние и оставляет x и y на своих местах (без выполнения < x, y>).

Пусть теперь ? представляет собой произвольную перестановку на множестве [n]: оно состоит из независимых (ненулевых) циклов, каждый из которых может быть поочередно возвращен в исходное состояние так, как показано выше, после чего x и y можно в случае необходимости поменять местами посредством <x, y>, что и требовалось доказать.