I Становление математических истин
Трижды счастливы души, которым дано
Подняться до истин подобных и звездное небо измерить!
Взорам их без помех дальние звезды открылись,
В цепи прочные мысли своей ширь эфира они заковали.
Так люди достигли небес — не как встарь,
В тщетной гордыне взгромоздивши горы на горы.
Овидий

Любая цивилизация, достойная так называться, занимается поиском истин. Мыслящие люди не могли не пытаться понять многообразие явлений природы, разгадать тайну появления на Земле человека, постичь смысл жизни и выяснить предназначение человека. Во всех древних цивилизациях, кроме одной, ответы на эти вопросы давались религиозными лидерами и принимались всеми. Единственным исключением была цивилизация, созданная древними греками. Греки совершили открытие, величайшее из когда-либо совершенных человеком: они открыли могущество разума. Именно греки классического периода, достигшего наивысшего расцвета в период VI-III вв. до н.э., поняли, что человек наделен способностью мыслить, наделен разумом, который, опираясь на наблюдение или опыт, способен открывать истины.
Нелегко ответить на вопрос о том, что привело греков к их открытию. Первые попытки осмыслить окружающий человека мир были сделаны в Ионии, греческих поселениях в Малой Азии, и многие историки пытались объяснить это сложившейся в Ионии общественно-политической обстановкой. Так, в Ионии была более свободная, чем в европейской Греции, политическая структура, что повлекло за собой определенное пренебрежение к традиционным религиозным верованиям. Однако наше знание греческой истории до VI в. до н.э. носит настолько фрагментарный характер, что невозможно дать сколько-нибудь исчерпывающее объяснение отмеченному феномену.
Со временем греки принялись размышлять над политическими системами, этикой, юриспруденцией, рациональными путями воспитания молодежи и многими другими видами человеческой деятельности. Их главный вклад, оказавший решающее влияние на всю последующую культуру, состоял в том, что они взялись за изучение законов природы. Прежде и греческая, и другие цивилизации древности рассматривали природу как нечто хаотичное, капризное и даже устрашающее. Все происходящее в природе было необъяснимо или приписывалось воле богов, умилостивить которых можно было молитвами, жертвоприношениями и другими ритуалами. Древние вавилоняне и египтяне, создавшие великие цивилизации за 3000 лет до н.э., заметили периодичность в движениях Солнца и Луны и даже разработали на этой основе календари, но не придавали своим открытиям особого значения. И эти исключительные по глубине и важности наблюдения не оказали решающего влияния на отношение людей к природе.
Греки осмелились взглянуть природе в лицо. Древнегреческие мыслители отвергли традиционные доктрины, веру в сверхъестественные силы, догму, сбросив путы, сдерживающие мысль. Греки первыми начали изучать разнообразные загадочные и сложные явления природы и предприняли попытку понять их. Свой разум они противопоставили хаосу на первый взгляд случайных явлений природы и вознамерились пролить на них свет.
Обладая беспредельной любознательностью и незаурядным мужеством, греки ставили вопросы (и находили ответы на них), которые служили пищей для серьезных размышлений и решались мыслителями высочайшего ранга. Лежит ли в основе всего, что происходит во Вселенной, некий единый план? Обязаны ли растения, животные, люди, планеты, свет, звук и т.д. своим появлением игре случая или же они являются частью какого-либо грандиозного плана? Обладая богатым воображением — что способствовало созданию нового взгляда на мир, — греки выработали концепцию Вселенной, ставшую основной на всех последующих этапах развития европейской мысли.
Греческие мыслители стали по-новому относиться к природе. Их отношение было рациональным, критическим и нерелигиозным. Греки отказались от мифов, равно как и от веры в богов, по своей прихоти правящих человеком и всем миром. Постепенно греческие мыслители создали учение об упорядоченной природе, бесперебойно функционирующей по единому плану. Все явления, доступные нашим органам чувств, — от движения планет до трепетания листьев на дереве — грекам удалось уложить в четкую, согласованную в деталях, понятную картину. Короче говоря, оказалось, что природа устроена рационально, и единый план, лежащий в ее основе, хотя и не поддается воздействию со стороны человека, вполне постижим.
Греки не только первыми принялись за поиск закона и порядка в природе, но и были первыми гениальными открывателями сокровенных схем, которым, как показывали наблюдения, следует природа. Так, греки дерзнули заняться поиском схемы, таящейся за грандиознейшими зрелищами, открытыми взору человека, — движением ослепительно сверкающего Солнца, сменой фаз Луны, чей лик являет богатейшую гамму оттенков, яркостью планет, бескрайней панорамой звездного неба, загадочными солнечными и лунными затмениями.
Первые попытки дать рациональное объяснение природы и устройства Вселенной предприняли ионийские философы в VI в. до н.э. Каждый из знаменитых философов этой эпохи: Фалес, Анаксимандр, Анаксимен, Гераклит и Анаксагор — пытался объяснить устройство Вселенной, принимая за основу какую-нибудь одну субстанцию. Фалес считал, например, что все состоит из воды, находящейся в газообразном, жидком или твердом состоянии. Объяснение многих явлений Фалес связывал с водой. Выбор его не столь неразумен, если учесть, что облака, туман, роса, дождь и град — различные состояния воды и что без воды нет жизни: она питает посевы и является основой органической жизни. Даже тело человека, как известно, на 90% состоит из воды.
Натурфилософия ионийцев представляла собой скорее набор дерзких умозаключений, хитроумных догадок и блестящих интуитивных прозрений, чем результат обширных и тщательно проведенных научных исследований. Философы ионийской школы так страстно стремились увидеть картину мира в целом, что обратились к широким обобщениям, минуя промежуточные этапы. Но вместе с тем они порвали с прежними представлениями, имевшими в основном мифологический характер, и предложили материалистическое, согласующееся с наблюдениями объяснение мироздания и природных явлений. Фантастические представления о природе ионийцы заменили рациональным подходом. Ионийцы дерзнули объять разумом Вселенную, перестав полагаться на богов, духов, призраков, демонов, ангелов и другие мистические силы, якобы управляющие явлениями природы. Квинтэссенцию воззрений ионийцев как нельзя лучше отражают слова Анаксагора: «Разум правит миром».
Решающим шагом, позволившим рассеять ореол таинственности и мистицизма, окружавший явления природы, и «навести порядок» в их кажущемся хаосе, стало применение математики. Этот шаг потребовал от греков не меньшей прозорливости, интуиции и глубины, чем вера в силу человеческого разума. План, по которому построена Вселенная, имеет математический характер — и только математика позволяет человеку открыть этот план.
Первой научной школой, предложившей свой вариант «математизированного плана» строения Вселенной, были пифагорейцы, возглавляемые Пифагором Самосским (около 585-500 гг. до н.э.). Пифагорийцы жили на юге Италии. Они черпали вдохновение и заимствовали свои взгляды из религиозных представлений греков, в которых центральное место отводилось очищению души и ее освобождению от скверны и узилища тела. Натурфилософия пифагорейцев носила ярко выраженный рациональный характер. Пифагорейцев поразило, что весьма различные в качественном отношении явления обладают одинаковыми математическими свойствами. Значит, решили пифагорейцы, именно математические свойства выражают сущность явлений. Если говорить более точно, то пифагорейцы видели сущность явлений в числе и числовых отношениях. В их объяснении природы числу отводилась роль начала начал. Пифагорейцы считали, что все тела состоят из фундаментальных частиц, «единиц бытия», которые в тех или иных комбинациях соответствуют различным геометрическим фигурам. В сумме эти единицы представляют материальный объект. Число было материей и формой Вселенной. Отсюда и основной тезис учения пифагорейцев: «Все вещи суть числа». А поскольку число выражало «сущность» всего, то объяснять явления следовало только с помощью чисел.
Учение пифагорейцев может показаться нам странным, потому что для нас числа — абстрактные понятия, а вещи — физические, или материальные, объекты. Привычное нам понятие числа возникло в результате абстрагирования — а ранним пифагорейцам эта абстракция была чужда. Для них числа были точками или частицами. Говоря о треугольных, квадратных, пятиугольных и других числах, которые мы сегодня называем фигурными, пифагорейцы имели в виду наборы точек, камешков, или других мелких предметов, расположенных в форме треугольников, квадратов и других геометрических фигур (рис. 1.1-1.4).

Рис. 1.1. Треугольные числа.

Рис. 1.2. Квадратные числа.
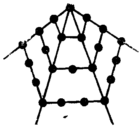
Рис. 1.3. Пятиугольные числа.

Рис. 1.4. Шестиугольные числа.
Хотя дошедшие до нас фрагменты исторических документов не позволяют установить точную хронологию событий, не вызывает сомнения, что пифагорейцы, развив и усовершенствовав свои учения, начали рассматривать числа как абстрактные понятия, а объекты — как конкретные реализации чисел. Именно в смысле такого более позднего различия, по-видимому, надлежит понимать высказывание знаменитого пифагорейца V в. до н.э. Филолая: «Если бы ни число и его природа, ничто существующее нельзя было бы постичь ни само по себе, ни в его отношении к другим вещам… Мощь чисел проявляется, как нетрудно заметить… во всех деяниях и помыслах людей, во всех ремеслах и музыке».
Свести музыку к простым отношениям чисел пифагорейцам удалось после того, как они совершили два открытия: во-первых, что высота тона, издаваемого колеблющейся струной, зависит от ее длины и, во-вторых, что гармонические созвучия издают одинаково натянутые струны, длины которых относятся между собой как целые числа ([5], с. 393-434). Например, гармоническое созвучие издают две одинаково натянутые струны, из которых одна вдвое длиннее другой. На современном языке интервал между тонами, издаваемыми такими двумя струнами, называется октавой. Другое гармоническое созвучие издают две струны, длины которых относятся как 3:2. В этом случае более короткая струна издает ноту, которая на квинту выше тона, издаваемого более длинной струной. Пифагорейцы разработали знаменитую музыкальную шкалу. Мы не будем, подробно останавливаться на музыке греческого периода. Заметим лишь, что многие греческие математики, в том числе Евклид и Птолемей, посвятили музыке, в частности гармоническим созвучиям и построению музыкальной шкалы, специальные сочинения.
Движения планет пифагорейцы также свели к числовым отношениям. Они считали, что тела, двигаясь в пространстве, издают звуки. Должно быть, на эту мысль их навело наблюдение: камень, раскручиваемый на веревке, со свистом разрезает воздух. Пифагорейцы полагали, что быстро движущееся тело издает более высокий звук, чем тело, движущееся медленно. Согласно астрономическим воззрениям пифагорейцев, планеты движутся тем быстрее, чем дальше они находятся от Земли. Звуки, издаваемые планетами, изменяются в зависимости от удаления от Земли и образуют гармоническое созвучие. Но эта «музыка сфер», подобно всякой гармонии, сводится к числовым отношениям, поэтому и движения планет также сводятся к числовым отношениям. Мы не слышим музыку небесных сфер потому, что привыкли к ней с самого рождения.
Другие явления природы также были сведены пифагорейцами к числам. Особую роль в учении пифагорейцев играли числа 1, 2, 3 и 4, образовывавшие тетрактис, или четверицу. По преданию, клятва пифагорейцев гласила: «Клянусь именем Тетрактис, ниспосланной нашим душам. В ней источник и корни вечно цветущей природы». Пифагорейцы считали, что все объекты в природе состоят из четверок, таких, как четыре геометрических элемента: точка, линия, поверхность и тело. Впоследствии Платон придавал особое значение четверке материальных элементов: земле, воздуху, огню и воде.
Сумма чисел, входящих в тетрактис, равна десяти, поэтому десять считалось идеальным числом и символизировало Вселенную. А поскольку число десять идеально, то в небесах должно было быть ровно десять тел. Поэтому пифагорейцы ввели центральный огонь, вокруг которого обращаются Земля, Солнце, Луна и пять известных в древности планет, а также Противоземля, расположенная по другую сторону от центрального огня. Центральный огонь и Противоземля невидимы, потому что поверхность Земли, на которой мы живем, скрывает их от нас. Вряд ли уместно входить в детали пифагорейской картины мира. Главное заключается в том, что пифагорейцы пытались построить астрономическую теорию на основе числовых отношений.
После того как пифагорейцы «свели» астрономию и музыку к числу, музыка и астрономия оказались связанными с арифметикой и геометрией и все четыре дисциплины стали считаться математическими. Они вошли в программу общего образования, причем это положение сохранилось вплоть до средневековья. В средние века комплекс общеобразовательных дисциплин, состоящий из арифметики, геометрии, музыки и астрономии, получил название квадривиум.
Общий итог пифагорейского отождествления числа и реального мира подведен в «Метафизике» Аристотеля:
В числах пифагорейцы усматривали (так им казалось) много сходного с тем, что существует и возникает, — больше, чем в огне, земле и воде (например, такое-то свойство чисел есть справедливость, а такое-то — душа и ум, другое — удача, и, можно сказать, в каждом из остальных случаев точно так же); так как далее они видели, что свойства и соотношения, присущие гармонии, выразимы в числах; так как, следовательно, им казалось, что все остальное по природе своей явно уподобляемо числам и что числа — первое во всей природе, то они предположили, что элементы чисел суть элементы всего существующего и что все небо есть гармония и число.
([6], т. 1, с. 75-76.)
Натурфилософию пифагорейцев лишь с большой натяжкой можно назвать состоятельной. Эстетические соображения, к которым примешивается навязчивое стремление найти числовые соотношения, не могли не приводить к утверждениям, выходящим за пределы реальных наблюдений. Пифагорейцам не удалось сколько-нибудь существенно продвинуть ни одну из областей физической науки. С полным основанием их теории можно было бы назвать поверхностными. Но то ли по счастливому стечению обстоятельств, то ли благодаря гениальной интуиции пифагорейцам удалось сформулировать два тезиса, общезначимость которых подтвердило все последующее развитие науки: во-первых, что основополагающие принципы, на которых зиждется мироздание, можно выразить на языке математики; во-вторых, что объединяющим началом всех вещей служат числовые отношения, которые выражают гармонию и порядок природы. Современная наука разделяет пифагорейскую приверженность числу, хотя, как мы увидим далее, современные теории представляют собой гораздо более искусную форму пифагореизма.
Более поздних философов, пришедших на смену пифагорейцам, не в меньшей мере интересовали природа реальности и математический план, лежащий в ее основе. Особое место среди преемников пифагорейцев занимают Левкипп (V в. до н.э.) и Демокрит (ок. 460-370 гг. до н.э.), наиболее отчетливо для своего времени сформулировавшие атомистическое учение. Согласно философии, которой они придерживались, мир состоит из бесконечного числа простых и вечных атомов. Атомы отличаются по форме, размерам, твердости, порядку и расположению. Все, что мы видим вокруг, представляет собой ту или иную комбинацию атомов. Хотя геометрические величины, например, отрезок прямой, бесконечно делимы, атомы являются мельчайшими, не поддающимися дальнейшему дроблению частицами. Одни свойства тел, такие, как форма, размеры или твердость, определяются свойствами атомов. Другие, как, например, вкус, тепло или цвет, определяются не самими атомами, а воздействием атомов на того, кто испытывает ощущения. Чувственное восприятие ненадежно, так как оно существенно зависит от индивидуума. Подобно пифагорейцам, атомисты утверждали, что реальность, лежащую в основе постоянно меняющегося многообразия физического мира, можно выразить на языке математики. Кроме того, атомисты считали, что все происходящее в мире строго предопределено математическими законами.
Самой влиятельной после пифагорейцев группой мыслителей, расширившей и распространившей учение о математическом плане, лежащем в основе природы, были платоники, возглавляемые, как о том говорит название этой школы, Платоном Афинским. Хотя Платон (427-347 гг. до н.э.) и заимствовал некоторые фрагменты учения пифагорейцев, в достопамятном IV в. до н.э. он был ведущей фигурой духовной жизни Греции. Платон основал в Афинах Академию — центр, который привлек к себе ведущих мыслителей его времени и существовал в течение девяти столетий.
Вера Платона в рациональность устройства Вселенной, вероятно, лучше всего выражена в его диалоге «Филеб»:
Сократ… Начнем же хотя бы со следующего вопроса…
Протарх. С какого?
Сократ. Скажем ли мы, Протарх, что совокупность вещей и это так называемое целое управляется неразумной и случайной силой как придется, или же, напротив, что целым правит, как говорили наши предшественники, ум и некое изумительное, всюду вносящее лад разумение?
Протарх. Какое же может быть сравнение, любезнейший Сократ, между этими двумя утверждениями! То, что ты сейчас говоришь, кажется мне даже нечестивым. Напротив, сказать, что ум ускоряет все, достойное зрелище мирового порядка — Солнца, Луны, звезд и всего круговращения небесного свода; да и сам я не решился был утверждать и мыслить об этом иначе.
([7], с. 33-34.)
Более поздние пифагорейцы и платоники проводили резкое различие между миром вещей и миром идей. Тела и отношения в материальном мире несовершенны, преходящи и тленны, но существует другой, идеальный, мир, в котором истины абсолютны и неизменны. Именно эти истины и надлежит рассматривать философу. О физическом же мире мы можем иметь только мнения. Видимый, чувственный мир не более чем смутная, расплывчатая и несовершенная реализация идеального мира: «вещи суть тени идей, отбрасываемых на экран опыта». Реальность надлежит искать в идеях чувственных, в физических объектах. Платон сказал бы, что в лошади, в доме или в прекрасной женщине нет ничего реального. Реальность заключена в универсальном типе (идее) лошади, дома или прекрасной женщины. Непреходящее знание может быть получено только относительно чистых идеальных форм. Только такие идеи постоянны и неизменны, и знание относительно них прочно и неуничтожимо.
Платон утверждал, что реальность и рациональность физического мира могут быть постигнуты только с помощью математики идеального мира. То, что идеальный мир устроен на математических началах, не вызывало сомнений. Плутарх приводит знаменитое изречение Платона: «Бог всегда является геометром». В диалоге «Государство» Платон говорит о том, что «знание, к которому стремятся геометры, есть знание вечного, а не того, что тленно и преходяще». Математические законы платоники считали не только сущностью реальности, но и вечными и неизменными. Числовые отношения также были частью реальности, а скоплениям вещей отводилась роль подобия чисел. Если у ранних пифагорейцев числа были имманентны (внутренне присущи) вещам, то у Платона числа стали трансцендентны вещам.
Платон пошел дальше пифагорейцев в том, что хотел не только понять природу с помощью математики, но и заменить математикой природу. Он считал, что более проницательный взгляд на физический мир дал бы возможность открыть основные истины, которые позволили бы разуму уже самостоятельно достроить все остальное. С момента обнаружения первичных истин дальнейшее было бы чистой математикой. Математика заменила бы физическое исследование.
В «Жизни Марцелла» Плутарх сообщает, что знаменитые современники Платона Евдокс и Архит использовали физические соображения для «доказательства» математических истин. Но Платон с негодованием отвергал такие доказательства как подрывающие основы геометрии, ибо они построены не на чистых рассуждениях, а на чувственных восприятиях.
Отношение Платона к астрономии дает ясное представление о том, к какого рода знанию надлежало, по его мнению, стремиться. Астрономия, утверждал Платон, не должна заниматься изучением движений наблюдаемых небесных тел. Расположение светил на небе и их видимые движения достойны всяческого восхищения и поистине прекрасны, но одни лишь наблюдения и объяснения движений далеко еще не составляют истинной астрономии. Дабы достичь истинной астрономии, необходимо «предоставить небеса самим себе», ибо истинная астрономия изучает законы движения истинных звезд в математических небесах, несовершенным подобием которых является видимое небо. Платон поощрял приверженность теоретической астрономии, занятие которой услаждает разум, а не тешит глаз, ибо ее объекты воспринимаются разумом, а не зрением. Различные фигуры, которые глаз видит на небе, надлежит использовать только как вспомогательные чертежи в поисках высших истин. К астрономии мы должны подходить, как к геометрии, рассматривая ее как серию задач, лишь подсказываемых наблюдаемыми светилами. Применения астрономии в навигации, при составлении календарей и вычислении времени для Платона интереса не представляли.
Совершенно иную концепцию изучения реального мира и отношения математики к реальности развил Аристотель, хотя он и был учеником Платона и много у Платона почерпнул. Аристотель критиковал Платона за идею о двух различных мирах и за сведение естественных наук к математике. Аристотель был физиком в буквальном смысле этого слова. В материальных телах он видел первичную субстанцию и источник реальности. По Аристотелю, физика и наука в целом должны заниматься изучением физического мира и извлекать истину из этих исследований. Подлинное знание достигается на основе чувственного опыта с помощью интуиции и абстрагирования. Абстракции не существуют независимо от человеческого разума.
Аристотель неоднократно подчеркивал, что универсалии — общие понятия — абстрагированы от реальных вещей. Для получения этих абстракций «мы начинаем с вещей познаваемых и наблюдаемых и переходим к вещам менее наглядным, которые по своей природе более понятны и более познаваемы». Аристотель брал наглядные, чувственные качества вещей, выхолащивал их и возводил до независимых, абстрактных понятий.
Какое место занимала математика в развитой Аристотелем схеме вещей? Основополагающими в схеме Аристотеля были физические науки. Математике отводилась вспомогательная роль в изучении природы при описании таких внешних свойств, как форма и размеры. Кроме того, математика помогала объяснять причины тех явлений, которые можно наблюдать в материальном мире. Так, геометрия может помочь в объяснении наблюдений из области оптики и астрономии, а арифметические пропорции могут служить основой гармонии. Но математические понятия и принципы заведомо являются абстракциями, корни которых уходят в реальный мир. Поскольку же они абстрагированы из реального мира, то они применимы к нему. Человеческий разум обладает особой способностью приходить к таким идеализированным свойствам физических объектов, отправляясь от ощущений, и создаваемые им абстракции с необходимостью должны быть истинными.
Даже нашего беглого обзора взглядов тех философов, которые сформировали духовный мир греков, достаточно, чтобы понять главное: все они подчеркивали необходимость изучения природы для понимания и оценки лежащей в основе всего сущего реальности. Кроме того, со времен пифагорейцев почти все философы утверждали, что природа устроена на математических основах. К концу классического периода окончательно сформировалось учение о природе, основанной на математических принципах, и начался планомерный поиск математических законов. Хотя это учение отнюдь не предопределило все последующее развитие математики, получив достаточно широкое распространение, оно оказало влияние на величайших математиков, в том числе и на тех, кто непосредственно не разделял его. Из всех достижений умозрительных построений древних греков подлинно новаторской была концепция космоса, в котором все подчинено математическим законам, постигаемым человеческим разумом.
Греки преисполнились решимости доискаться до истин и, в частности до истин о математических основах природы. Как следует приступить к поиску истин и как при этом гарантировать, что поиск действительно приводит к истинам? Греки предложили «план» такого поиска. Хотя он создавался постепенно на протяжении нескольких веков (VI-III вв. до н.э.) и историки науки расходятся во мнениях относительно того, когда и кем этот план был впервые задуман, к III в. до н.э. «план поиска истин» был доведен до совершенства.
Математика в широком смысле слова, понимаемая как всевозможное использование чисел и геометрических фигур, родилась за несколько тысячелетий до того, как ей занялись греки классического периода. Она включает в себя достижения многих исчезнувших цивилизаций, среди которых наиболее выдающуюся роль сыграли культуры древнего Египта и Вавилона. Но во всех древних цивилизациях, за исключением греческой, математика еще не сформировалась в отдельную науку, у нее не было своей особой методологии, и она не ставила перед собой иных целей, кроме решения самых непосредственных, практических задач. Математика была своего рода инструментом, набором разрозненных нехитрых правил, позволявших людям удовлетворять повседневные запросы: составлять календари, назначать сроки проведения сельскохозяйственных работ, вести торговлю. Открытые методом проб и ошибок, на основе опыта и наблюдений, многие из этих правил были верны лишь приближенно. О математике догреческих цивилизаций в лучшем случае можно сказать, что она в известной мере продемонстрировала мощь, если не строгость, мышления и проявила больше упорства, чем блеска. Математику такого рода принято называть эмпирической. Эмпирическая математика египтян и вавилонян стала прелюдией к тому, что создали греки.
Хотя греческая культура не была полностью свободной от внешних влияний (греческие мыслители, совершая путешествия в Египет и Вавилон, знакомились там с достижениями местной науки) и хотя математике в современном смысле этого слова (даже в столь благоприятной интеллектуальной атмосфере древней Греции) еще предстояло пройти период созревания, то, что создали греки, значительно отличалось от того, что они по крупицам собрали из опыта своих предшественников.
Провозгласив своей целью поиск математических истин, греки не могли опираться на грубые, эмпирические, ограниченные, несвязные и во многих случаях приблизительные результаты, накопленные до них главным образом египтянами и вавилонянами. Сама математика, основные факты о числах и фигурах, должна была стать сводом абсолютных истин — и математические рассуждения, направленные на постижение истин о физических явлениях, например о движениях небесных тел, должны были приводить к неоспоримым результатам. Высокие цели намечены, но как их достичь?
Первый принцип, которого неуклонно придерживались греки, состоял в том, что математика должна иметь дело с абстракциями. Для философов, творцов греческой математики, носителями истины могли быть лишь перманентные, неизменяемые сущности и отношения. К счастью, человеческий разум, работу которого стимулируют наши органы чувств, может подняться до более высоких концепций — идей, вечных реалий и истинных объектов мышления. Предпочтение, отдаваемое греками абстракции, имело под собой и другую причину. Чтобы обрести мощь, математика должна охватывать в едином абстрактном понятии существенные черты всех физических реализаций этого понятия. Так, математическая прямая должна отражать наиболее существенные особенности натянутых нитей, краев линеек, границ сельскохозяйственных угодий и траекторий лучей света. Математическая прямая не должна, следовательно, иметь толщину, цвет, молекулярную структуру или испытывать натяжение. Греки вполне отчетливо и явно утверждали, что их математика имеет дело с абстракциями. В «Государстве» Платон говорит о геометрах следующее:
Разве ты не знаешь, что, хотя они используют видимые формы и рассуждают о них, мыслят они не о самих формах, а об идеалах, с которыми не имеют сходства; не о фигурах, которые они чертят, а об абсолютном квадрате и абсолютном диаметре… и что в действительности геометры стремятся постичь то, что открыто лишь мысленному взору?
Итак, математика должна заниматься прежде всего изучением таких абстрактных понятий, как точка, прямая и целое число. Другие понятия, например треугольник, квадрат и окружность, можно определить через основные понятия, которые, как отметил Аристотель, должны оставаться неопределимыми, ибо в противном случае у нас не было бы отправной точки. О степени изощренности греческой математики можно судить хотя бы по тому, что определяемые там понятия должны были иметь аналоги в реальности либо по доказанному, либо по построению. Так, нельзя было ввести по определению трисектор угла и доказывать о нем теоремы: трисектор мог бы и не существовать. И так как грекам не удалось решить задачу о трисекции любого угла при тех ограничениях, которые они накладывали на геометрические построения, то они так и не ввели понятия трисектора.{7}
Свои рассуждения о математических понятиях греки начинали с аксиом — истин, столь очевидных, что в справедливости их невозможно усомниться. Такие истины грекам были известны. Платон обосновал принятие аксиом своей теорией воспоминаний — анамнезисом. Как уже упоминалось, Платон считал объективно существующим мир идей. До того как человек появляется на свет, его душа обретается в мире идей и впитывает впечатления. Побуждаемая к воспоминаниям, душа затем восстанавливает накопленные ранее впечатления, чтобы признать истинность аксиом геометрии. Никакой земной опыт ей для этого не требуется. Аристотель подошел к проблеме иначе. Истинность аксиом, утверждает он во «Второй аналитике» ([8] гл. 18), мы познаем посредством безошибочной интуиции. Кроме того, аксиомы необходимы нам как основа для рассуждений. Если бы в своих рассуждениях мы использовали факты, истинность которых неизвестна, то для установления их истинности потребовались бы новые рассуждения, и так до бесконечности. В результате мы бесконечно «спускались» бы в наших доказательствах — но нигде не могли бы остановиться. Среди аксиом Аристотель различал общие понятия и постулаты. Общие понятия истинны во всех областях мысли. К их числу относятся такие утверждения, как «Если от равного отнять равные [части], то остаются равные же [части]» ([8], с. 199). Постулаты применимы к такой специфической области, как геометрия. Таково, например, утверждение «Две [разные] точки определяют прямую и притом только одну». Аристотель считал, что постулаты не обязательно должны быть самоочевидными, но если они не очевидны, то их истинность надлежит подтверждать выводимыми из них следствиями. Математики же требовали самоочевидности постулатов.
Из аксиом с помощью рассуждений выводятся заключения. Существует много типов рассуждений, например рассуждения по индукции, по аналогии и дедукции. Правильность заключения гарантирует лишь один из многих типов рассуждений. Заключение «Все яблоки красные», сделанное на основании того, что тысяча просмотренных яблок оказались красными, индуктивно и поэтому не абсолютно надежно. Заключение «Джон сможет окончить этот колледж», сделанное потому, что брат Джона, унаследовавший от родителей те же способности, окончил колледж, получено с помощью рассуждения по аналогии и заведомо не надежно. С другой стороны, дедуктивное рассуждение, несмотря на множество различных форм, гарантирует истинность заключения. Так, допуская, что все люди смертны и Сократ — человек, следует прийти к заключению, что Сократ смертен. Используемое в этом рассуждении правило логики является одной из форм суждения, которое Аристотель назвал силлогистическим выводом. К правилам дедуктивного рассуждения Аристотель относил также закон противоречия (никакое высказывание не может быть одновременно истинным и ложным) и закон исключенного третьего (любое высказывание должно быть либо истинным, либо ложным).
Аристотель, а вслед за ним и весь мир приняли за неоспоримую истину, что применение правил дедуктивного вывода к любым посылкам гарантирует получение заключений, не уступающих по надежности посылкам. Иначе говоря, если посылки истинны, то истинны и заключения. Следует отметить, в особенности для обсуждения в дальнейшем, что Аристотель абстрагировал правила дедуктивной логики из рассуждений, которыми тогда уже широко пользовались математики.{8} Дедуктивная логика — дитя математики.
Хотя почти все греческие философы считали дедуктивный вывод единственно надежным методом получения истины, Платон придерживался несколько иных взглядов. Не выдвигая возражений против дедуктивного доказательства, Платон тем не менее считал его поверхностным, поскольку математические аксиомы и теоремы существуют в некотором объективном, независимом от человека мире, и в соответствии с учением Платона об анамнезисе человеку необходимо лишь вспомнить эти аксиомы, чтобы сразу же распознать их неоспоримую истинность. Теоремы, если воспользоваться сравнением из диалога Платона «Теэтет», подобны птицам в птичнике. Они существуют сами по себе, и необходимо лишь «схватить» их. В диалоге Платона «Менон» Сократ с помощью искусно поставленных вопросов вытягивает из молодого раба утверждение, что площадь квадрата, построенного на гипотенузе равнобедренного прямоугольного треугольника, вдвое больше площади квадрата, построенного на любом из катетов. Сократ торжествующе заключает, что искусно поставленные вопросы помогли рабу, никогда не изучавшему геометрию, вспомнить теорему.
Важно правильно оценивать, сколь радикальной была приверженность дедуктивному доказательству. Предположим, что некий ученый, измерив сумму углов ста различных треугольников, отличающихся расположением, размерами и формой, обнаружил, что в пределах точности измерений сумма углов всегда оказывается равной 180°. Разумеется, ученый решил бы, что сумма углов любого треугольника равна 180°. Но его доказательство было бы индуктивным, а не дедуктивным — и поэтому неприемлемым с точки зрения математики. Он мог бы точно так же проверить сколько угодно четных чисел и убедиться, что каждое из них представимо в виде суммы двух простых чисел. Но подобная проверка не является дедуктивным доказательством, и ее результат не сочли бы за математическую теорему. Итак, мы видим, что дедуктивность доказательства — требование весьма ограничивающее. Тем не менее греческие математики, бывшие в большинстве своем философами, упорно настаивали на исключительном использовании дедуктивных рассуждений, так как именно дедукция приводит к абсолютным истинам, к вечным ценностям.
Предпочтение, отдаваемое философами дедуктивным рассуждениям, обусловлено еще одной причиной. Философов интересуют лишь самые общие факты, касающиеся человека и физического мира, а чтобы установить такие универсальные истины, как то, что человек по существу добр, что в мире царит порядок или что человеку есть ради чего жить, дедуктивный вывод из подходящих исходных принципов осуществим в гораздо большей мере, чем индукция или рассуждение по аналогии.
Еще одну причину того, что греки классического периода отдавали предпочтение дедукции, можно усмотреть в организации их общества. Философией, математикой и искусством, естественно, увлекались прежде всего состоятельные люди, а не те, кто занимался физическим трудом. Все домашнее и общественное хозяйство держалось на рабах, метеках (свободных людях, не имевших, однако, гражданских прав){9} и на свободных гражданах — ремесленниках; они же представляли все важнейшие профессии. Образованные свободные граждане не занимались физическим трудом и редко участвовали в торговых сделках. Платон провозгласил, что профессия лавочника недостойна свободнорожденного, и предложил подвергать наказанию всякого гражданина, который унизит себя подобным занятием, как совершившего преступление. Аристотель утверждал, что в идеальном государстве ни один гражданин (в отличие от рабов) не должен заниматься никаким ремеслом. Беотийцы (одно из греческих племен) запрещали тем, кто запятнал себя участием в торговых сделках, в течение десяти лет занимать общественные должности. В таком обществе эксперимент и наблюдение были мыслителям чужды. Считалось, что источники такого рода не могут помочь получить результаты научного, в частности математического, характера.
Хотя приверженность греков дедуктивному доказательству имела под собой немало оснований, не вполне ясно, кто из философов или какая группа мыслителей впервые продемонстрировали эту приверженность. Наши знания учений и трудов философов — до Сократа — носят, к сожалению, весьма фрагментарный характер, и, хотя на этот счет неоднократно высказывались различные мнения, ни одно из них не получило общего признания. Мы можем лишь с уверенностью утверждать, что во времена Аристотеля требование дедуктивности соблюдалось неукоснительно, так как Аристотель, формулируя в явном виде стандарты строгости, отмечает необходимость неопределяемых терминов и правил логического вывода.
Насколько удалось грекам осуществить свой план установления математических законов Вселенной? К счастью, лучшие достижения греческой математики, созданной усилиями Евклида, Аполлония, Архимеда и Клавдия Птолемея, дошли до нас. Хронологически все эти авторы относятся ко второму великому периоду греческой культуры, получившему название эллинистического или александрийского (300 г. до н.э. — 600 г. н.э.). В IV в. до н.э. царь Филипп Македонский предпринял попытку покорить персов, господство которых распространялось на весь Ближний Восток. Персы были традиционными врагами европейских греков. Филипп был убит, и на трон вступил его сын Александр. Александр Македонский разгромил персов и перенес культурный центр своей безмерно расширившейся империи в новый город, который он с присущей ему «скромностью» назвал в свою честь Александрией. Александр Македонский умер в 323 г. до н.э., но его план создания нового центра подхватили и продолжили его преемники в Египте, вошедшие в историю под именем династии Птолемеев.
Достоверно установлено, что Евклид жил и преподавал в Александрии около 300 г. до н.э. (сам Евклид скорее всего получил образование в Платоновской Академии в Афинах). Это почти единственная информация, которой мы располагаем о частной жизни Евклида. Свои труды Евклид облекал в форму обширных систематических дедуктивных обзоров отдельных открытий многих греческих авторов классического периода. В главном труде Евклида — «Началах» излагаются основные свойства пространства и пространственных фигур.
«Началами» Евклида отнюдь не исчерпывается его вклад в развитие геометрии пространства. Он посвятил коническим сечениям не дошедшее до нас сочинение, а уроженец города Перга в Малой Азии Аполлоний (262-190 гг. до н.э.), изучавший математику в Александрии, продолжил исследование параболы, эллипса и гиперболы и написал по этому предмету классический труд — «Конические сечения».
Архимед (287-212 гг. до н.э.), возможно получивший образование в Александрии{10}, но живший на Сицилии, добавил к чисто геометрическим достижениям греков трактаты: «О шаре и цилиндре», «О коноидах и сфероидах» и «Квадратура параболы», посвященных вычислению площадей и объемов сложных фигур и тел по методу, предложенному Евдоксом (390-337 гг. до н.э.) и получившему впоследствии название метод исчерпывания. В наши дни подобные задачи решаются методами интегрального исчисления.
Греки внесли еще один крупный вклад в изучение пространства и пространственных фигур: они создали тригонометрию. Ее основы были заложены Гиппархом, который жил на Родосе и в Александрии и умер около 125 г. до н.э. Его труд был продолжен Менелаем (ок. 98 г. н.э.), а полное и вполне авторитетное изложение астрономии дал египтянин Клавдий Птолемей (умер в 168 г. н.э.), работавший в Александрии. Главный труд Птолемея «Большое математическое построение астрономии» более известен под арабским вариантом названия — «Альмагест».{11} Тригонометрия занимается изучением количественных соотношений между сторонами и углами треугольника. Греков интересовали главным образом треугольники на поверхности сферы со сторонами, образованными дугами больших кругов (так называются круги, плоскость которых проходит через центр сферы), поскольку именно такие сферические треугольники находили применение при изучении движений планет и звезд, перемещавшихся, как считали греки, по дугам больших кругов. Но ту же теорию можно «перенести» и на случай треугольников на плоскости. Именно этот вариант — плоская тригонометрия — входит в программу современной средней школы. Введение тригонометрии потребовало весьма основательных познаний в арифметике и даже некоторого знакомства с алгеброй. В дальнейшем (гл. V) мы узнаем о достижениях греков в этих областях математики.
Достигнутые успехи превратили математику из свода неясных, эмпирических, разрозненных фрагментов в блестящую, обширную, систематическую и глубокую науку. Классические труды Евклида, Аполлония и Архимеда («Альмагест» Птолемея является исключением), посвященные изучению свойств пространства и пространственных фигур, могут показаться весьма специальными и не позволяют составить верное представление о более широкой значимости излагаемого в них материала. Может создаться впечатление, что эти чисто геометрические сочинения имеют весьма косвенное отношение к раскрытию истинных тайн природы. Ведь все классические труды посвящены лишь изложению формализованной, изысканной, дедуктивной математики. В этом отношении греческие математические тексты не отличаются от современных учебников и монографий по математике. Авторы таких книг видят свою главную задачу в организации и связном изложении полученных математических результатов и считают излишним как-либо обосновывать важность излагаемых разделов науки и игнорируют возможные эвристические соображения и разбор частных случаев, подкрепляющих правдоподобность доказываемых теорем, а также умалчивают о возможных применениях своих конструкций. Многие историки науки, специализирующиеся на изучении греческой математики классического периода, склонны поэтому считать, что математики той эпохи занимались математикой ради математики, и в подтверждение своих слов ссылаются на два величайших компилятивных сочинения классического периода — «Начала» Евклида и «Конические сечения» Аполлония. Но те, кто так утверждает, чрезмерно сужают поле зрения. Ограничиваться рассмотрением только «Начал» и «Конических сечений» — это то же самое, что, исходя из одной лишь работы Ньютона о разложении бинома, утверждать, что Ньютон был чистым математиком.
Подлинной целью греков было исследование природы. Этой цели служило все — даже геометрические истины высоко ценились лишь постольку, поскольку они были полезны при изучении физического мира. Греки понимали, — что в структуре Вселенной воплощены геометрические принципы, первичным компонентом которых является пространство. Именно поэтому исследование пространства и пространственных фигур явилось существенным вкладом в изучение природы. Геометрия входила составной частью в более широкую программу космологических исследований. Например, изучение сферической геометрии было предпринято, когда астрономия приобрела математический характер, что произошло во времена Платона. Греческое слово «сфера» (шар) у пифагорейцев имело тот же смысл, что и (тогда еще не существовавшее) слово «астрономия». Сочинение Евклида «Феномены», посвященное сферической геометрии, предназначалось для использования в астрономии. Подобные факты и более полное знание того, как происходило развитие математики в последующие времена, позволяют утверждать, что и у греков к постановке математических проблем приводили естественнонаучные исследования и что математика была неотъемлемой частью изучения природы. Чтобы прийти к такому выводу, не нужно строить умозрительные заключения — достаточно выяснить, чего именно удалось достигнуть грекам в исследовании природы и кому принадлежат самые крупные достижения.
Величайший успех в области собственно физической науки выпал на долю астрономии. Платон, хорошо осведомленный о впечатляющем числе астрономических наблюдений, проведенных в Древнем Египте и Вавилоне, неоднократно подчеркивал, что египтяне и вавилоняне не располагали основополагающей, обобщающей теорией, которая позволила бы объяснить наблюдаемые нерегулярные движения планет. Положение дела попытался «исправить» некогда учившийся в Академии Евдокс, чья чисто геометрическая работа включена в V и XIII книги «Начал» Евклида. Полученное Евдоксом решение составило первую в истории науки в разумных пределах завершенную астрономическую теорию.
Мы не станем подробно описывать теорию Евдокса. Скажем лишь, что это была сугубо математическая теория, рассматривавшая движения взаимодействующих сфер. За исключением сферы неподвижных звезд, все сферы в теории Евдокса были не материальными телами, а математическими конструкциями. Евдокс даже не пытался установить, какие силы вынуждают сферы вращаться так, как они, по его утверждению, вращались. Теория Евдокса весьма современна нам по духу, ибо и в настоящее время целью науки зачастую считается математическое описание, а не физическое объяснение. Теория Евдокса была превзойдена теорией, создание которой принято приписывать трем величайшим астрономам-теоретикам: Аполлонию, Гиппарху и Птолемею. Эта теория вошла в «Альмагест» Птолемея.
Никакие труды Аполлония по астрономии до нашего времени не дошли. Однако различные греческие авторы, в том числе Птолемей (в XII книге «Альмагеста»), ссылаются на его результаты. Как астроном, Аполлоний пользовался такой известностью, что получил прозвище ? (эпсилон), поскольку он много занимался движением Луны, а Луну греческие астрономы обозначали буквой ?. До нас дошло лишь одно небольшое астрономическое сочинение Гиппарха, но в «Альмагесте» Птолемея мы находим ссылки на Гиппарха и восхваления в его адрес.
Основная схема того, что теперь принято называть птолемеевой системой мира, вошла в греческую астрономию в период между работами Евдокса и Аполлония. Согласно этой схеме, планета P движется с постоянной скоростью по окружности с центром S, в то время как центр S в свою очередь движется по окружности, центр которой совпадает с Землей E (рис. 1.5). Окружность, по которой движется точка S, называется деферентом, окружность, которую описывает планета P, — эпициклом. Точка S для некоторых планет совпадает с Солнцем, а в остальных случаях это просто математическая точка. Направления, в которых движутся точки P и S, могут как совпадать, так и быть противоположными. Например, в случае Солнца и Луны точки S и P движутся по окружностям в противоположные стороны.
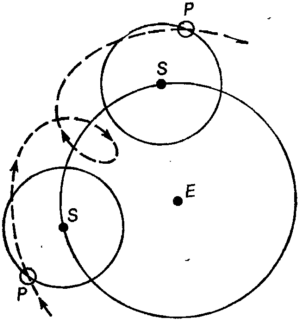
Рис. 1.5. Эпицикл и деферент.
Для описания движений некоторых планет Птолемей несколько видоизменил описанную схему. Подходящим образом выбирая радиусы эпицикла и деферента, скорости движения тела по эпициклу и скорости движения эпицикла по деференту, Гиппарх и Птолемей смогли получить описания движений небесных тел, хорошо согласующиеся с результатами астрономических наблюдений того времени. Со времен Гиппарха лунное затмение можно было бы предсказать с точностью до одного-двух часов, хотя солнечные затмения удавалось предсказывать менее точно. Такие предсказания стали возможными, потому что Птолемей применил тригонометрию, разработанную им, по его собственному признанию, для астрономии.
Как и Евдокс, Птолемей отчетливо сознавал (и это необходимо особо отметить, имея в виду нашу главную тему — поиск истин), что его теория представляет собой не более чем удобное математическое описание, согласующееся с наблюдениями, и не обязательно должна отражать истинный механизм движения планет. При описании движений некоторых планет Птолемею приходилось рассматривать несколько альтернативных схем, и он отдавал предпочтение той, которая была проще с точки зрения математики. В XIII книге «Альмагеста» Птолемей утверждает, что астрономия должна стремиться к возможно более простой математической модели. Но христианский мир принял математическую модель Птолемея за абсолютную истину.
Теория Птолемея дала первое полное, в разумных пределах, подтверждение постоянства и неизменности природы и была воспринята как окончательное решение поставленной Платоном проблемы объяснения видимых движений небесных тел. Никакой другой из полученных в греческую эпоху результатов не может соперничать с «Альмагестом» по глубине влияния на представления о Вселенной, и ни одно сочинение, за исключением «Начал» Евклида, не обрело столь беспрекословного авторитета.
Разумеется, в нашем кратком очерке греческой астрономии не названы многие другие достижения античных астрономов и не дано полного представления о глубине и размахе свершений тех, кого мы здесь упомянули. Греческая астрономия достигла высокого уровня развития и наглядности и весьма широко применяла математику. Кроме того, почти каждый греческий математик, в том числе и такие мастера, как Евклид и Архимед, занимался астрономией.
Постижение физических истин не закончилось на геометрии пространства и астрономии. Греки заложили также основы механики. Механика изучает движение тел, которые можно рассматривать как материальные точки, движение протяженных тел и силы, вызывающие эти движения. В своей «Физике» ([6], т. 3, с. 59-262) Аристотель свел воедино все высшие достижения греческой механики. Как и вся аристотелева физика, его механика опирается на рациональные самоочевидные принципы, согласующиеся с наблюдениями. Хотя эта теория сохранила влияние на протяжении почти двух тысячелетий, мы не останавливаемся на ее изложении, так как она была полностью вытеснена механикой Ньютона. Существенными дополнениями к аристотелевой теории движения стали работы Архимеда по определению центров тяжести тел и его теория рычага. Во всей этой деятельности для нас наиболее существенна ведущая роль математики; тем самым получило подтверждение всеобщее убеждение в том, что в постижении законов природы первостепенное значение имеет математика.
Не меньший интерес, чем астрономия и механика, вызвала оптика. Основы этой науки также были заложены греками. Почти все греческие философы, начиная с пифагорейцев, строили умозрительные заключения о природе света, зрения и цвета, но нас интересуют математические достижения в этой области. Первым было априорное утверждение Эмпедокла (около 490 г. до н.э.) из Агригента — города на острове Сицилия — о том, что свет распространяется с конечной скоростью. Хронологически первыми систематическими исследованиями света, сохранившимися до нашего времени, стали сочинения Евклида «Оптика» и «Катоптрика»{12}. В «Оптике» Евклид рассматривает проблемы зрения и использования зрения для определения размеров различных предметов. В «Катоптрике» (теории зеркал) показано, как ведут себя лучи света при отражении от плоских, выпуклых и вогнутых зеркал и как ход лучей сказывается на том, что мы видим. Как и «Оптика», «Катоптрика» начинается с определений, которые в действительности являются постулатами. Теорема I (аксиома в современных учебниках и монографиях), играющая основополагающую роль в геометрической оптике известна как закон отражения. Она утверждает, что угол ? образуемый с поверхностью зеркала лучом света, падающим на зеркало из точки P, равен углу, образуемому с поверхностью зеркала отраженным лучом (рис. 1.6). Евклид также установил закон падения для луча, падающего на выпуклое и вогнутое зеркала: в точке касания Евклид заменил зеркало касательной плоскостью R (рис 1.7) «Оптика» и «Катоптрика» — сочинения математические не только по содержанию, но и по своей структуре. Основное место в них, как и в «Началах» Евклида, отводится определениям, аксиомам и теоремам.
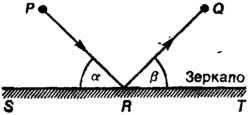
Рис. 1.6. Отражение от плоского зеркала.
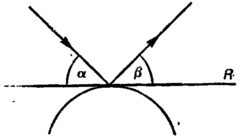
Рис. 1.7. Отражение от выпуклого зеркала.
Математик и инженер Герон (I в.) вывел из закона отражения важное следствие. Если P и Q на рис. 1.6 — любые две точки, расположенные по одну сторону от прямой ST, то из всех путей, ведущих из точки P к прямой ST, a затем к точке Q, кратчайший соответствует такому положению точки R, при котором отрезки прямых PR и QR образуют с прямой ST равные углы. Следовательно, луч света, идущий из точки P к зеркалу и затем к точке Q, распространяется по кратчайшему пути. Отсюда ясно, что природа весьма «сведуща» в геометрии и использует ее с наибольшей пользой. Теорема, которую мы только что воспроизвели, заимствована нами из «Катоптрики» Герона, где рассмотрено также отражение луча света от вогнутых и выпуклых зеркал, а также от комбинаций зеркал.
Об отражении света от зеркал различной формы было написано великое множество работ. Среди ныне безвозвратно утерянных сочинений — «Катоптрика» Архимеда, «О зажигательном зеркале» Аполлония (около 190 г. до н.э.) и «О зажигательных зеркалах» Диоклеса (около 190 г. до н.э.). Зажигательные зеркала были вогнутыми и имели форму сферического сегмента параболоида вращения (поверхности, образованной вращением параболы вокруг ее оси) и эллипсоидов вращения. Аполлонию было известно, а в книге Диоклеса содержалось доказательство, что параболическое зеркало, отражая свет от источника света, помещенного в его фокусе, собирает лучи в пучок, параллельный оси зеркала (рис. 1.8). Наоборот, если пучок падающих лучей направить параллельно оси параболического зеркала, то после отражения лучи соберутся в фокусе. Собранные в фокусе солнечные лучи вызывают резкий разогрев и способны зажечь помещенный в фокусе горючий материал, откуда и название — зажигательное зеркало. По преданию, Архимед, воспользовавшись этим свойством зажигательных зеркал, сконцентрировал солнечные лучи на римских судах, блокировавших с моря его родной город Сиракузы, и поджег неприятельский флот. Аполлонию были известны отражательные свойства и других конических сечений. Он знал, например, что все лучи, выходящие из одного фокуса эллиптического зеркала, после отражения собираются в другом фокусе. В книге III «Конических сечений» приведены соответствующие геометрические свойства эллипса и гиперболы.
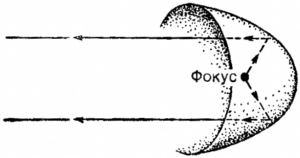
Рис. 1.8. Отражение от параболического зеркала.
Греки заложили основы многих других наук. Особенно велика их роль как основоположников географии и гидростатики. Эратосфен из Кирены (около 284-192 гг. до н.э.), один из наиболее образованных людей античности, директор Александрийской библиотеки, вычислил расстояния между многими населенными пунктами на той части Земли, которая была известна древним грекам. Ему также принадлежит широко известное ныне вычисление длины окружности Земли. В своей «Географии» Эратосфен помимо описаний используемых им математических методов объяснил причины изменений, происходящих на поверхности Земли.
Самым обширным сочинением по географии была «География» Птолемея в восьми книгах. В ней Птолемей не только дополнил и расширил труд Эратосфена, но и определил положение на поверхности Земли восьми тысяч мест, указав те самые их широты и долготы, которыми мы пользуемся и поныне. Птолемей изложил также методы составления карт, применяемые и в современной картографии, в частности метод стереографической проекции. Во всех трудах по географии основную роль играла сферическая геометрия, которую греки применяли с IV в. до н.э.
Гидростатика занимается изучением давления, оказываемого жидкостью на погруженное в нее тело. Здесь основополагающим трудом по праву считается сочинение Архимеда «О плавающих телах». Как и все остальные сочинения, о которых мы упоминали, оно чисто математическое как по своему подходу, так и по способу получения результатов. В частности, именно в этом сочинении сформулирован знаменитый принцип, известный ныне под названием закона Архимеда, который гласит, что на погруженное в жидкость тело действует выталкивающая сила, равная весу вытесненной телом жидкости. Таким образом, мы обязаны Архимеду объяснением того, каким образом человек может остаться на плаву в мире сил, стремящихся утопить его.
Хотя в александрийский период дедуктивный подход к математике и математическому изложению законов природы играет главенствующую роль, следует отметить, что в отличие от своих предшественников классического периода александрийцы не отказывались от экспериментов и наблюдений. Так, александрийцы использовали результаты высокоточных астрономических наблюдений, которые в течение двух тысячелетий производили вавилоняне. Гиппарх составил каталог звезд, наблюдавшихся в его время. Среди изобретений александрийцев (сделанных главным образом Архимедом, а также математиком и инженером Героном) мы находим солнечные часы, астролябии и устройства для использования энергии пара и воды.
Особую известность приобрел Александрийский музей, основанный непосредственным преемником Александра Македонского в Египте — Птолемеем Сотером. Музей стал родным домом ученых; его библиотека насчитывала около 400 тыс. томов. Поскольку ее хранилища не могли вместить все рукописи, еще 300 тыс. томов были размещены в храме Сераписа. Ученые не только занимались наукой, но и проводили занятия с учениками.
Своими математическими трудами и многочисленными исследованиями греки существенно подкрепили тезис о том, что Вселенная зиждется на математических принципах. Математика внутренне присуща природе, является истиной о структуре природы, или, если воспользоваться выражением Платона, реальностью о физическом мире. Закон и порядок существует в природе, и математика — ключ к пониманию этого порядка. Более того, человеческий разум способен проникнуть в сокровенный план природы и открыть математическую структуру Вселенной.
Толчком к созданию концепции логического, математического подхода к познанию природы послужили, по-видимому, «Начала» Евклида. Хотя сочинение Евклида предназначалось для изучения физического пространства, структура самого сочинения, его необычайное остроумие и ясность изложения стимулировали аксиоматическо-дедуктивный подход не только к остальным областям математики, например к теории чисел, но и ко всем естественным наукам. Через «Начала» Евклида понятие логической структуры всего физического знания, основанного на математике, стало достоянием интеллектуального мира.
Тем самым греки установили союз математики и изучения явлений природы, который стал фундаментом всей современной науки. Вплоть до конца XIX в. поиск математических принципов, лежащих в основе природы, был поиском истины. Глубокое убеждение в том, что математические законы открывают истины о природе, привлекало к математике самых глубоких и возвышенных мыслителей.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК