6. ТЕОРЕМА ГЁДЕЛЯ

На теорему Гёделя о неполноте ссылается множество людей. Ее приводят как аргумент в пользу своих утверждений физики, инженеры, философы, психологи, биологи, моралисты, педагоги и даже искусствоведы. Но как часто бывает с эпохальными результатами, все говорят о теореме Гёделя, но очень мало кто имеет о ней адекватное представление и еще меньше таких, которые читали её аутентичный текст. До сих пор не имеется русского перевода знаменитой статьи. Это объясняется тем, что в свое время статья Гёделя интересовала только специалистов по математической логике, а все они тогда владели немецким языком. Когда же значение теоремы Гёделя стало выходить за рамки математики, появились компактные и методологически более совершенные ее изложения.

Однако именно изложение Гёделя имеет огромный интерес. Метод, которым сам Гёдель доказал свою теорему, ценен в такой же степени, как и его результат. Вообще, если подходить к вопросу с философской позиции, то метод тут неотделим от результата. Ниже мы, не стремясь, конечно, к какой-либо строгости, очертим общий ход рассуждений Гёделя, сопровождая схему доказательства некоторыми комментариями. Но сначала несколько слов об авторе теоремы.

Курт Гёдель родился в Праге (Чехия в то время входила в состав Австро-Венгрии) в 1906 году. Главные свои открытия он сделал в возрасте 24 лет (заметим, что и Ньютон написал свои лучшие работы примерно в таком же возрасте), однако и в дальнейшем получал крупные научные результаты, относящиеся, в частности, к теории множеств; в 1949 г. он предложил новый тип решения уравнений общей теории относительности, заслужив похвалу Эйнштейна[1]. В настоящее время Гёдель живет в Соединенных Штатах и является профессором Института высших исследований в Принстоне, штат Нью-Джерси. В 1951 г. он был удостоен высшей награды, присуждаемой в США за научные достижения, Эйнштейновской премии.

В статье, в которой доказывалась теорема о неполноте формальной арифметики, Гёдель исследует систему формальной арифметики Principia Mathematica (он называет эту аксиоматически-дедуктивную теорию «системой PM»). Начинает он свою статью следующими словами: «Развитие математики в направлении все увеличивающейся строгости привело, как известно, к формализации многих ее частей, так что стало возможным доказывать теоремы, не пользуясь ничем, кроме нескольких механических правил. Наиболее широкие формальные системы, построенные к настоящему времени, это, с одной стороны, система Principia Mathematica (РМ) и, с другой стороны, система аксиом Цермело—Френкеля для теории множеств (развитая в дальнейшей Дж. фон Нейманом).

Обе эти системы настолько широки, что все методы доказательства, применяемые ныне в математике, в них формализованы, то есть сведены к небольшому числу аксиом и правил вывода. Поэтому можно предположить, что этих аксиом и правил вывода окажется достаточным, чтобы получить ответ на любой математический вопрос, который вообще может быть формально выражен в этих системах. Ниже будет показано, что это не так, что, наоборот, в обеих упомянутых системах имеются проблемы даже относительно простые, относящиеся к теории обычных целых чисел, которые нельзя решить, исходя из аксиом. Это обстоятельство не связано с какой-то специфической природой этих систем, напротив, оно имеет силу для очень широкого класса формальных систем, к которым, в частности, принадлежат все системы, получающиеся из упомянутых двух посредством присоединения к ним конечного числа аксиом, если только это присоединение не приводит к тому, что доказуемым становится какое-либо ложное предложение»[2].

Далее Гёдель излагает формальную систему, эквивалентную РМ, вводя только несущественные модификации, которые должны облегчить доказательство теоремы. Как и во всяком формальном исчислении, в основе этой системы лежат: перечень основных символов, определение комбинаций символов, называемой формулой, список постулатов — аксиом и правил вывода. С характером этих понятий читатель уже знаком, и нам остается рассказать о том, каким образом у Гёделя вводятся натуральные числа.

Это делается так: вводится символ для числа «нуль» (0), а также символ «следования за» f, который трактуется так, что f0 есть единица, ff0 — два и т. д.

Но для целей, которые преследует Гёдель, недостаточно иметь лишь символы для логических операций и чисел. Нужно выразить также основные арифметические предикаты, такие, как «простое число», «делится нацело» и т. п. В этом месте Гёдель, используя понятия системы РМ и известную в математике процедуру рекурсивного задания функции, то есть задания новых значений функции через предыдущие (рекурсивно, например, определяется функция «факториал» — произведение всех натуральных чисел от единицы до данного числа: (1)0! = 1; (2) (n+ 1)! = (n!) (n + 1)), вводит понятие рекурсивной функции, которое заведомо выразимо средствами формальной арифметики. Делается это так: задаются исходные рекурсивные функции — константа 0 и функция «следования за» — а затем устанавливается способ, с помощью которого из них можно получать более сложные рекурсивные функции. В самом начале этой части работы Гёдель показывает, что такие важные функции, как сложение, умножение и возведение в степень, рекурсивны. Он определяет также понятие рекурсивного арифметического предиката; n-местным арифметическим рекурсивным предикатом (отношением между n числами) называется такой предикат, который определяется уравнением φ (х1, х2,..., хn) = 0, где φ—рекурсивная функция, а х1, х2, ..., >Хn — переменные для чисел. Примером рекурсивного предиката является двуместный предикат «меньше». Рассмотрим этот случай подробнее, так как в дальнейшем нам понадобится представление о рекурсивных функциях и предикатах.

1. Функция δ, определяемая условиями

а) δ(0)=0, б) δ(у+1)= y,

рекурсивна, как выраженная стандартной схемой рекурсии через исходные рекурсивные функции (здесь прибавление единицы к числу следует понимать как взятие следующего числа в натуральном ряду).

2. Функция х ∸ у, определяемая условиями

а) х ∸ О = х, б) х ∸ (у+1)=δ(х ∸ у),

рекурсивна, как выраженная стандартной схемой рекурсии через рекурсивную функцию δ. Как нетрудно убедиться, смысл функции х ∸ у (она называется усеченным вычитанием) таков: функция эта равна х — у, если х >= у и равна нулю, если х < у.

В самом деле, посмотрим, каково значение функции х ∸ у для х, у = 0, 1, 2, 3 (над знаками равенств помечаем какой пункт определений 1, 2 применяется или какое из ранее полученных значений функции х — у используется):

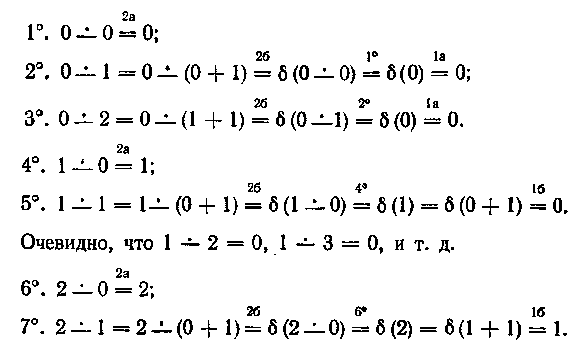
Подобным же образом вычисляется 0∸3=0,0∸4=0 (вообще, легко усматривается, что при дальнейшем возрастании значения у выражение 0 ∸ у будет оставаться равным нулю).

При дальнейшем возрастании значения y выражение 2 ∸ у становится равным нулю. Аналогично вычисляется, что 3 ∸ 0 = 3, 3 ∸ 1 = 2, 3 ∸ 2 = 1, но при y > 2 выражение 3 ∸ y равно нулю.

3. Предикат, опередляемый уравнением х ∸ у = 0, рекурсивен; это очевидно, поскольку функция х ∸ у, как мы показали, рекурсивна. Но смысл этого предиката выражается в обычном языке утверждением x <= у.

Далее, можно показать рекурсивность предиката строгого неравенства, так как для его выражения в формальной системе арифметики нужно использовать теперь только функцию взятия следующего числа («прибавление единицы»).

Несколько раньше введения рекурсивных функций Гёдель осуществляет важную процедуру, которая впоследствии была названа гёделевской нумерацией, или гёделизацией. Это — процедура нумерации всех символов, встречающихся в формальном арифметическом исчислении.

Сначала нумеруются знаки логических операций, вспомогательные символы и другие исходные знаки: символ 0 получает номер 1; символ f — номер 3; символ ~ — номер 5; символ V — номер 7; символ Ɐ — номер 9; символ ), то есть левая скобка, — номер 11; символ ), то есть правая скобка, — номер 13. Таким образом, для нумерации исходных знаков используются нечетные числа от 1 до 13. Символы импликации, конъюнкции и эквиваленции и квантор существования в исчислении Гёделя не фигурируют; эти логические операции могут быть выражены через отрицание, дизъюнкцию и квантор общности.

Далее нумеруются переменные x1, у1, z1,..., вместо которых в арифметические формулы подставляются числа. Для этого используются простые числа, начиная с 17. Аналогичным способом нумеруются предикатные переменные x2, y2, z2,... (переменные, на места которых в формулах подставляются знаки свойств и отношений), только для нумерации используются квадраты простых чисел, начиная с 17 (символ х2 получает номер 17², символа y2— номер 19² и т. д.).

Затем следует нумерация последовательностей символов (частным случаем которых являются формулы). Здесь правило присвоения номеров таково: если имеется последовательность из k символов, имеющих номера соответственно n1, n2, ... nk, то номер этой последовательности имеет вид: 2ⁿ¹ * Зⁿ² * 5ⁿ³- ... pk^nk, где pk — k-тое простое число, начиная с двух. Покажем наглядно, как «работает» в этом случае гёделизация. Пусть дана формула Vх1(х2(х1)) (она читается: «Для всякого натурального числа x1 выполняется свойство х2). Найдем ее гёделев номер. Выпишем по порядку гёделевы номера входящих в формулу символов: 9, 17,11,289,11,17,13,13. Номер N рассматриваемой формулы таков:

N=2⁹ • З¹⁷ • 5¹¹ • 7²⁸⁹• 11¹¹• 13¹⁷ • 17¹⁸ • 19¹³.

Наконец, нумеруются последовательности формул. Если дана последовательность из 5 формул с номерами m1, m2, m3..., m_s, то номер последовательности определяется как 2^m1 • 3^m2 • 5^m3 • ... • p_s^ms, где p_s — 5-тое простое число.

Используя рекурсивные функции, Гёдель показывает, что с помощью проведенной нумерации все «метаарифметические» высказывания, то есть высказывания об арифметических объектах, можно представить как соотношения между числами (гёделевыми номерами). Скажем, утверждение «Данная комбинация символов есть формула» выражается некоторым арифметическим предикатом от гёделева номера этой комбинации n, то есть записывается в виде некоторой арифметической формулы q2n.

Аналогично, утверждение «Данная последовательность формул является доказательством» предстает в виде арифметического предиката от номера этой последовательности. Показывается, что арифметизируются и высказывания вида: «Данная формула есть результат подстановки в такую-то формулу вместо такой-то переменной такой-то формулы», «Данная формула доказуема» (то есть существует последовательность формул, являющаяся доказательством, которая кончается на данной формуле) и т. д. Проведя такую работу, Гёдель показал фактически, что исчисление можно значительно «ужать», эаменив символы, формулы и доказательства некими представляющими их числами, а утверждения о формулах можно превратить в арифметические формулы.

Решающий момент в построении Гёделя наступает тогда, когда он предъявляет формулу, которая представляет в его системе кодировки метавыоказывание о собственной недосказуемости. В этом случае возникает следующая ситуация. Предположим, что формула, говорящая «Я недоказуема», доказуема. Тогда, если логико-арифметическая система непротиворечива — и, значит, все доказуемые в ней формулы (тождественно)истинны[3], данная формула не может быть доказуемой; в самом деле, если бы она была доказуемо и, то заключенное в ней утверждение «Я недоказуема» следует считать истинным, то есть признать формулу недоказуемой[4]. Но данная формула не только недоказуема, но и неопровержима, то есть недоказуемо ее отрицание. Таким образом, формулу, имеющую смысл «Я недоказуема», в системе «типа РМ» нельзя ни доказать, ни опровергнуть —это неразрешимая формула.

Существование же в формальной системе неразрешимой формулы — и к тому же содержательно истинной, так как ее смысл «Я недоказуема» соответствует ситуации в данной системе, означает неполноту системы. Заметим, наконец, что формула с таким смыслом на деле является схемой формул вида «Я формула Ф;, недоказуема», — так что в системе оказывается бесконечное множество неразрешимых высказываний, получаемых различным выбором значений Ф⁵.

Итак, если формальная арифметика («типа РМ») непротиворечива, то она неполна. А что если она противоречива? Тогда ее теоремы теряют всякую ценность, поскольку в этом случае доказывается, что можно доказать любую наперед заданную теорему —для этого достаточно даже одного-единственного противоречия между доказанной формулой и доказанным ее отрицанием. В этом случае, конечно, гёделева формула, говорящая «Я недоказуема», будет доказуема, но будет доказуемо и ее отрицание. Математики всей душой надеются, что арифметика непротиворечива. Но нельзя ли эту надежду превратить в твердую уверенность и доказать непротиворечивость формальной арифметики?

Исследование Гёделя привело к следующему результату. С помощью своего метода кодировки Геделю удалось доказать в логико-арифметическом исчислении формулу, метаматематический смысл которой таков: «Если формальная арифметика непротиворечива, то формула, говорящая «Я недоказуема», доказуема» (обозначим эту формулу через (*)). Предположим теперь, что мы сумели в рассматриваемом исчислении доказать формулу, утверждающую непротиворечивость формальной арифметики. Тогда, в силу доказанной Гёделем формулы (»), по модесу поненсу следует заключение, что формула, говорящая «Я недоказуема», доказуема. Но это противоречит предыдущей теореме (называемой теоремой о неполноте, или первой теоремой Гёделя). Поэтому получается, что формулу, говорящую о непротиворечивости формальной арифметики, доказать в этой последней нельзя, если только сама формальная арифметика не противоречива. Если же она противоречива, то в ней, как мы отметили выше, доказуема любая формула, в том числе и формула, которую можно считать выражающей наличие у данной формальной системы свойства «быть непротиворечивой».

Методологическое заключение из этой теоремы (называемой второй теоремой Гёделя) таково: если формальная арифметика непротиворечива, то ее непротиворечивость нельзя доказать средствами, формализуемыми в ней самой, то есть теми финитными средствами, которыми Гильберт хотел ограничить метаматематические исследования.

Мы все время говорим о формальной арифметике, но результаты Гёделя относятся к любому формальному исчислению, достаточно богатому, чтобы содержать в себе арифметику, то есть к исчислению, «начиная с арифметики». Исчисление высказываний беднее арифметики, поэтому на него теорема Гёделя не распространяется — и, как мы знаем, легко доказать его непротиворечивость (оно также полно). Таким образом, работы Гёделя были первыми строгими исследованиями возможностей дедуктивного метода познания. И эти исследования привели к результатам, которые никак не могла предвидеть наука «догелевского» периода.

'Открытия Гёделя вызвали множество толкований. Общим их мотивом — полностью убедительным —- является заключение об определенной внутренней ограниченности регулярных процедур дедуктивного и вычислительного характера, о невозможности представления процесса расширения знания (начиная с математики) и в виде завершенной формальной системы. Как отметил П. С. Новиков, «понятия и принципы всей математики не могут быть полностью выражены никакой формальной системой, как бы мощна она ни была»[6]. Но это так же мало означает дискредитацию метода построения формальных систем, как открытие предельности скорости света — дезавуацию физической теории пространства и времени. Из «ограничительных» результатов математической логики — эти результаты не исчерпывались открытиями Гёделя, о которых шла речь, а получили дальнейшее продолжение в большой серии теорем, касающихся неразрешимости и неполноты формальных теорий, тем более не следует заключение о превосходстве интуиции над разумом.

Гносеологические выводы из теоремы Гёделя нужно делать с большой осторожностью. То, на что наталкивает нас в философском плане эта теорема, высказано Э. Нагелем и Дж. Ньюменом в следующей форме: «Заключения, к которым пришел Гёдель, порождают, естественно, вопрос, можно ли построить вычислительную машину, сравнимую по своим «творческим» математическим возможностям с человеческим мозгом. Современные вычислительные машины обладают некоторым точно фиксированным запасом команд, которые умеют выполнять их элементы и блоки; команды соответствуют фиксированным правилам вывода некоторой формализованной аксиоматической процедуры. Таким образом, машина решает задачу, шаг за шагом выполняя одну из «встроенных» в нее заранее команд. Однако, как видно из гёделевской теоремы о неполноте, уже в элементарной арифметике натуральных чисел возникает бесчисленное множество проблем, выходящих за пределы возможностей любой конкретной аксиоматической системы, а значит, и недоступных для таких машин, сколь бы остроумными и сложными ни были их конструкции и с какой бы громадной скоростью ни проделывали они свои операции. Для каждой конкретной задачи в принципе можно построить машину, которой эта задача была бы под силу, но нельзя создать машину, пригодную для решения любой задачи. Правда, и возможности человеческого мозга могут оказаться ограниченными, так что и человек тогда сможет решить не любую задачу. Но даже если это так, структурные и функциональные возможности человеческого мозга пока еще намного больше по сравнению с возможностями самых изощренных из мыслимых пока машин... Единственный непреложный вывод, который мы можем сделать из гёделевской теоремы о неполноте, состоит в том, что природа и возможности человеческого разума неизмеримо тоньше и богаче любой из известных пока машин»[7].

Действительно, электронная вычислительная машина есть универсальный инструмент вычисления, о чем пойдет речь ниже. Конечно, в самой схеме ЭВМ вовсе не заложен аксиоматически-дедуктивный метод получения теорем. Но машину в принципе всегда можно «научить» выводить теоремы с помощью заданных правил вывода из заданных аксиом (правда, соответствующие программы могут оказаться очень сложными). В результате машина «овладевает» дедуктивным методом доказательства теорем и, естественно, оказывается подвластной ограничениям, которые налагают на этот процесс положения Гёделя. Но эти же самые ограничения распространяются ина человека, если он работает строго по дедуктивному методу[8].

Впрочем, ограничения, вытекающие из результатов Гёделя, относятся не к дедуктивному методу вообще, а к таким дедуктивным системам, которые содержат теорию натуральных чисел и в которых доказательства представляют собой эффективно распознаваемые (за конечное число шагов) объекты. Но как показало последующее развитие математической логики, проблему непротиворечивости и другие проблемы, касающиеся формальных систем, можно исследовать методами, выходящими за пределы подобного финитизма, но представляющимися достаточно надежными. На этом пути становится возможным, например, доказательство непротиворечивости классической формальной арифметики[9].

Результаты Гёделя, во всяком случае, раскрывают важную особенность определенного аппарата, служащего знанию с большой эффективностью, поэтому часто принимавшегося за аппарат абсолютный и окончательный, аппарата формальной выводимости. Лишая аксиоматически-дедуктивный метод (коль скоро он пользуется лишь средствами строго финитного характера) статуса абсолютного, они разрушают его гипнотическое влияние на математиков и логиков и заставляют их не отождествлять более этот метод с дедуктивным методом вообще, искать новые способы построений, ведущих к познанию истины. В этом заряде антидогматизма заключена большая философ. екая ценность теоремы о неполноте. Она заставляет размышлять над тем, что такое знаковое моделирование реальности, что такое строгая теория и сколь разнообразными могут быть ее разновидности»