Глава 9 Искусство математической магии
Глава 9
Искусство математической магии
Я всегда получал удовольствие от игры с цифрами. Я нахожу арифметику такой же занимательной, как и магию. Но понимание магических секретов арифметики требует знаний алгебры. Конечно, есть и другие причины для ее изучения. Назову лишь несколько: сдача экзаменов, моделирование проблем из реального мира, программирование и возможность понимания высшей математики. Но интерес к алгебре у меня вызвало в первую очередь желание понять некоторые математические трюки. Их я вам сейчас и представлю!
ЭКСТРАСЕНСОРНАЯ МАТЕМАТИКА
Попросите добровольца в аудитории загадать любое число, состоящее из одной-двух цифр. Затем скажите, что никоим образом не можете знать, что это за число, и предложите сделать следующее.
1. Удвойте число.
2. Прибавьте 12.
3. Разделите сумму на 2.
4. Вычтите из нее исходное число.
Спросите: «Думаете ли вы сейчас о цифре 6?» Опробуйте этот трюк сначала на себе и увидите, что данная последовательность вычислений всегда в итоге приводит к цифре 6, какое бы число вы изначально ни выбрали.
Почему это работает
Этот трюк целиком основан на простой алгебре. Я иногда использую его как способ познакомить с алгеброй студентов.
Секретное число, выбранное добровольцем, можно обозначить как х. Тогда выполняемые действия представляем так:
1. 2х (удвоить число).
2. 2х + 12 (прибавить 12).
3. (2х + 12)/2 = х + 6 (разделить на 2).
4. х + 6 — х (вычесть исходное число).
Не важно, какое число выбрано, итоговый ответ всегда будет 6. При повторении данного приема попросите добровольца прибавить другое число на втором шаге (скажем, 18). Итоговый ответ будет половиной этого числа (а именно 9).
МАГИЯ ЧИСЛА 1089
Следующий трюк существует уже не одно столетие. Сделайте так, чтобы человек из аудитории достал ручку и бумагу:
1) и тайно записал трехзначное число, цифры которого идут в порядке уменьшения (например, 851 или 973);
2) записал число в обратном порядке и вычел его из исходного числа;
3) к полученному ответу добавил его же, только в обратном порядке.
В конце последовательности магическим образом появится ответ 1089, какое бы число ни выбрал доброволец. Например:
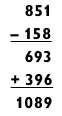
Почему это работает
Независимо от того, какое трехзначное число вы или кто-либо другой выберете в этой игре, окончательный ответ всегда будет равен 1089. Почему? Обозначим аbс неизвестное трехзначное число. Алгебраически это эквивалентно:
100a + 10b + c.
Запись числа в обратном порядке (для вычитания из исходного) дает сbа, которое алгебраически равно:
100c + 10b + a.
После вычитания сbа из аbс выходит:
100a + 10b + c — (100c + 10b + a) = 100(a — c) + (c — a) = 99(a — c).
Поэтому после вычитания на шаге 2 должно получиться одно из следующих чисел, кратных 99: 297, 396, 495, 594, 693, 792 или 891. Каждое из них после прибавления к нему своей перевернутой версии в итоге даст 1089, что мы и видим на шаге 3.
ТРЮК С ПРОПУЩЕННОЙ ЦИФРОЙ
Используя число 1089 из предыдущего примера, вручите добровольцу калькулятор и попросите умножить 1089 на любое трехзначное число, не называя его. (Предположим, он тайно умножил 1089 х 256 = 278 784) Теперь поинтересуйтесь, сколько цифр в полученном ответе. Ответ — 6.
Затем попросите: «Громко назовите пять из этих шести цифр в любом порядке. Я попытаюсь определить недостающую». Предположим, доброволец громко перечисляет: «Два… четыре… семь… восемь… восемь». Вы вежливо говорите ему, что он пропустил цифру 7. Секрет основан на том, что число кратно 9 тогда, и только тогда, когда сумма составляющих его цифр кратна 9. Так как 1 + 0 + 8 + 9 = 18 кратно 9, значит, число 1089 кратно 9. Поэтому 1089 при умножении на любое целое число даст кратное 9. И раз уж прозвучавшие цифры в сумме дают 29, и следующее кратное 9, большее 29, это 36, то наш доброволец пропустил число 7 (так как 29 + 7 = 36).
Есть более утонченные способы заставить добровольца в конечном итоге прийти к кратному 9. Вот некоторые из моих любимых.
1. Пусть он наугад выберет шестизначное число, перемешает его цифры, затем отнимет меньшее из шестизначных чисел из большего. Поскольку мы производим вычитание двух чисел с одинаковой модульной суммой (в самом деле, сумма цифр идентична), полученная в итоге разность будет иметь нулевую модульную сумму, следовательно, число будет кратно 9. Далее продолжайте действовать, как было описано выше, чтобы найти недостающую цифру.
2. Пусть он тайно выберет любое четырехзначное число, запишет его в обратном порядке, а потом вычтет меньшее число из большего. (Получится кратное 9.) Затем пусть умножит результат на 3. Далее, как и раньше, вы ищете пропущенную цифру.
3. Попросите добровольца перемножать разные цифры до тех пор, пока их произведение не превратится в семизначное число. Это не гарантия получения числа, кратного 9, но на практике такую «гарантию» можно получить не меньше чем в 90 % случаев (с большой вероятностью перемножаемые цифры будут включать девятки или две тройки, или две шестерки, или 3 и 6). Я часто использую данный способ, выступая перед математически продвинутой публикой, которая может раскусить другие методы.
Однако существует одна проблема, за которой нужно постоянно следить. Предположим, прозвучавшие числа в сумме дают кратное 9 (скажем, 18). После такого ответа у вас не будет возможности определить, пропущен ли 0 или 9. Как справиться с этой ситуацией? Очень просто! Сжульничайте! Просто спросите: «Вы ведь не пропустили 0, не так ли?» Если 0 пропущен, то вы успешно провернули свой трюк. Если нет, скажите: «Ой, просто показалось, что вы отвлеклись! Вы не пропустили один, два, три или четыре, не так ли?» Доброволец либо покачает головой, либо скажет «нет». Затем вы продолжаете: «Как и не пропустили пять, шесть, семь или восемь. Вы не включили девять, не так ли?» Доброволец ответит утвердительно, а вы получите заслуженные аплодисменты!
СЛОЖЕНИЕ ЧЕХАРДА
Этот прием сочетает в себе быстрые вычисления в уме и поразительные предсказания. Вручите зрителю карту с расчерченными на ней десятью линиями, пронумерованными от 1 до 10.
Пусть он загадает два положительных числа от 1 до 20 и подпишет ими линии 1 и 2. Далее попросите его записать сумму 1-й и 2-й линий на линии 3. Затем сумму линии 2 и 3 на линии 4 и так далее, как проиллюстрировано ниже.

Пусть зритель покажет вам карту. Вы сразу же можете назвать ему сумму всех чисел на ней. Например, в нашем случае вы могли бы мгновенно объявить, что числа в сумме дают 671 (быстрее, чем зритель подсчитал бы это с калькулятором).
В качестве приза вручите зрителю калькулятор и попросите его разделить число на линии 10 на число с линии 9. В данном примере получится частное 257/159 = 1,616. Пусть он произнесет первые три цифры частного, а после перевернет карточку (там вы уже написали свое предсказание). Он будет очень удивлен увиденным 1,61!
Почему это работает
Для выполнения быстрого расчета нужно просто умножить число с линии 7 на 11. Здесь 61 х 11 = 671. Причина эффективности этого приема проиллюстрирована в таблице ниже. Если обозначить числа на линиях 1 и 2 как х и у соответственно, а затем просуммировать числа на всех линиях от 1 до 10, то в итоге выйдет 55х + 88у, что составляет 11 х (5х + 8у). А это равно произведению числа 11 на число на линии 7.

Что касается прогнозирования, то здесь используется тот факт, что для любых положительных чисел a, b, c, d, если a/b < c/d, то значение дроби, которая получается путем «ошибочного сложения дробей» (то есть путем сложения числителей и сложения знаменателей), будет лежать между двумя исходными дробями. Другими словами, применяем неравенства:
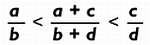
Таким образом, частное от деления числа на линии 10 на число на линии 9, (21х + 34у)/(13х + 21у), должно быть между
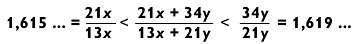
Следовательно, частное должно начинаться с цифр 1,61, как и было предсказано.
По сути, если продолжать такую «чехарду» до бесконечности, отношение последовательно идущих значений будет все ближе подбираться к значению

Это число с настолько огромным количеством удивительно красивых и загадочных свойств, что его часто называют золотым отношением (золотым сечением).
МАГИЧЕСКИЕ КВАДРАТЫ
Вы готовы к испытанию совершенно иного рода? Ниже размещен пример «магического квадрата». Сколько же о нем было написано еще во времена Древнего Китая! Но мы расскажем о способе создания магических квадратов в развлекательном стиле. Эту заученную схему я исполнял годами.
Я показываю визитку со следующей надписью на задней стороне:
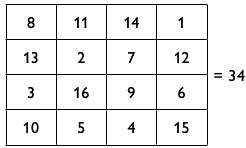
И говорю: «Перед вами магический квадрат. Это самый маленький магический квадрат, который можно создать, используя числа от одного до шестнадцати. Здесь суммы чисел в каждой строке и каждом столбце дают одно и то же число — тридцать четыре. Я провел весьма широкое исследование на тему магических квадратов, поэтому предлагаю создать один прямо на ваших глазах».
Затем я прошу кого-либо из аудитории назвать любое число больше 34. Предположим, это будет 67. После достаю еще одну визитку, рисую пустую сетку «4 на 4» и помещаю число 67 справа от нее. Далее прошу человека указывать на квадраты по одному, в любом порядке. Как только он указывает на пустую клетку, я незамедлительно записываю в нее число.
Конечный результат выглядит так:
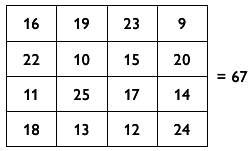
Я продолжаю: «В случае с первым магическим квадратом каждая строка и каждый столбец при сложении давали тридцать четыре. (На этом этапе я обычно откладываю карточку с квадратом в сторону.) Теперь посмотрим, что у нас получилось с новым квадратом». Убедившись, что элементы каждой строки и каждого столбца действительно дают в сумме 67, я говорю: «Но я не останавливаюсь на этом. Специально для вас я решил пойти еще на один шаг дальше. Обратите внимание, что обе диагонали при сложении дают шестьдесят семь!» Затем я указываю на то, что сумма четырех квадратов в левом верхнем углу тоже равна 67 (16 + 19 + 22 + 10 = 67), как и остальных квадратов такого же размера! «Они все в сумме равны шестидесяти семи. Но не верьте мне на слово. Пожалуйста, оставьте себе магический квадрат в качестве сувенира и проверьте его потом сами!»
КАК СОСТАВИТЬ МАГИЧЕСКИЙ КВАДРАТ
Вы можете создать магический квадрат, который при суммировании давал бы любое число, воспользовавшись исходным магическим квадратом с суммой 34. Держите его при этом на виду. Пока вы чертите сетку «4 на 4», устно выполните следующие вычисления.
1. Вычтите 34 из заданного числа (например, 67–34 = 33)
2. Разделите полученное число на 4 (например, 33/4 = 8 с остатком 1)
Частное — это первое «магическое» число. Частное плюс остаток — второе «магическое» число. (Здесь магические числа 8 и 9.)
3. Когда доброволец указывает на пустой квадрат, незаметно взгляните на квадрат 34, чтобы узнать, какой квадрат ему соответствует. Если это квадрат с числами 13, 14, 15 или 16, прибавьте к ним второе число (в нашем примере 9). Если нет, то прибавьте первое магическое число (8).
4. Вставляйте подходящее число до тех пор, пока не закончите составление магического квадрата.
Обратите внимание: когда заданное число четное, но не кратное 4, ваши первое и второе магические числа будут одинаковыми. Так что у вас будет только одно магическое число для прибавления его к числам из квадрата 34.
Почему это работает
Этот метод работает потому, что каждая строка, столбец и диагональ из исходного магического квадрата при сложении дают 34. Предположим, заданное число 82. Так как 82–34 = 48 (и 48/4 = 12), то следует прибавлять 12 к каждому числу в каждой ячейке исходного магического квадрата. В результате каждая «группа четверок», которая до этого равнялась 34, будет при сложении давать 34 + 48 = 82. Можете убедиться в этом на примере следующего магического квадрата.
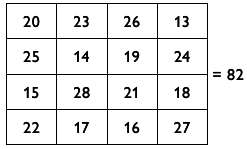
С другой стороны, если бы заданным числом было 85, магическими числами были бы 12 и 15. Поэтому мы прибавим 15 к квадратикам, которые содержат числа 13, 14, 15 и 16. Так как каждые строка, столбец и квадрат «2 на 2» содержат одно из этих чисел, то каждая группа из 4 клеток будет при сложении давать 34 + 12 х 3 + 15 = 85, как в следующем магическом квадрате.
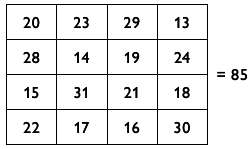
В качестве интересного математического пустячка позвольте отметить еще одно удивительное свойство знаменитого магического квадрата «3 на 3», показанного ниже.
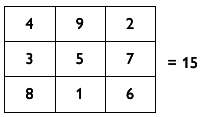
В нем не только строки, столбцы и диагонали дают в сумме 15, но если вы представите строки магического квадрата как трехзначные числа, то сможете удостовериться с помощью калькулятора, что 4922 + 3572 + 8162 = 2942 + 7532 + 6182. Так же как 4382 + 9512 + 2762 = 8342 + 1592 + 6722. Если вам любопытно, почему так происходит, вы найдете ответ в моей статье Magic «Squares» Indeed! («В самом деле “магические” квадраты!»), ссылка на которую дана в библиографии.
БЫСТРЫЕ КУБИЧЕСКИЕ КОРНИ
Попросите кого-нибудь выбрать двузначное число, но не называть его. Затем попросите возвести это число в куб, то есть умножить само на себя трижды, используя калькулятор. Например, если секретное число 68, пусть доброволец вычислит 68 х 68 х 68 = 314 432 и назовет ответ. Как только он произнесет его вслух, вы можете мгновенно раскрыть секрет исходного числа — это кубический корень 68. Как это делается?
Чтобы быстро вычислять кубические корни, нужно выучить кубы чисел от 1 до 10.
13 = 1
23 = 8
33 = 27
43 = 64
53 = 125
63 = 216
73 = 343
83 = 512
93 = 729
103 = 1000
Как только вы запомните эти значения, вычислять кубические корни станет так же легко, как и назвать значение числа ?. Приведем пример.
Чему равен кубический корень из 314 432?
Кажется, что это довольно сложное задание для начала, но не паникуйте, на самом деле оно довольно простое. Как обычно, будем двигаться постепенно.
1. Посмотрите на величину тысяч, 314 в данном примере.
2. Поскольку 314 лежит между 63 = 216 и 73 = 343, то кубический корень находится в диапазоне «60 плюс» (так как 603 = 216 000 и 703 = 343 000). Следовательно, первая цифра кубического корня будет 6.
3. Для определения последней цифры заметьте, что только куб числа 8 оканчивается на 2 (83 = 512), так что последней цифрой будет 8.
Поэтому кубический корень из 314 432 равен 68. Три простых шага — и вы у цели. Обратите внимание, что каждая цифра от 0 до 9 появляется по одному разу в виде последней цифры куба.
А теперь попрактикуйтесь.
Чему равен кубический корень из 19 683?
1. 19 находится между 8 и 27 (23 и 33).
2. Следовательно, кубический корень лежит в диапазоне «20 плюс».
3. Последняя цифра в задаче 3, что соответствует 343 = 73, значит, 7 и будет последней цифрой.
Ответ: 27.
Обратите внимание, что наши выводы по поводу последней цифры работают только тогда, когда исходное число является кубом целого числа. Например, кубический корень из 19 684 будет 27,0004572… Определенно не 27. Вот почему эта тема включена в раздел математической магии, а не в более ранние главы. (Кроме того, расчеты производятся настолько быстро, что кажется, будто без магии не обошлось!)
УПРОЩЕННЫЕ КВАДРАТНЫЕ КОРНИ
Квадратные корни так же просто вычислить, если задан полный квадрат. Например, если кто-то сказал вам, что квадрат двузначного числа равен 7569, то вы в состоянии мгновенно ответить, что исходное число (квадратный корень) равно 87. Вот как это делается.
1. Посмотрите на величину сотен (цифры, предшествующие последним двум) в данном примере.
2. Так как 75 находится между 82 (8 х 8 = 64) и 92 (9 х 9 = 81), то нам известно, что квадратный корень будет где-то в диапазоне «80 плюс». Следовательно, его первая цифра 8.
Существует два числа, квадраты которых заканчиваются на 9: 32 = 9, 72 = 49. Поэтому последняя цифра квадратного корня должна равняться 3 или 7. Таким образом, квадратный корень равен либо 83, либо 87. Какой из них?
3. Сравните исходное число с квадратом числа 85 (который можно легко посчитать как 80 х 90 + 25 = 7225). Так как 7569 больше, чем 7225, квадратный корень будет б?льшим числом, то есть 87.
Решим еще один пример.
Чему равен квадратный корень из 4761?
Поскольку 47 лежит между 62 = 36 и 72 = 49, ответ должен находиться в диапазоне «60 плюс». Если последняя цифра квадрата равна 1, то последняя цифра квадратного корня должна быть 1 или 9. Так как 4761 больше 652 = 4225, то квадратный корень должен равняться 69. Как и с предыдущим трюком для кубического корня, этот метод можно использовать только тогда, когда исходное число является полным квадратом.
УДИВИТЕЛЬНАЯ СУММА
Следующий трюк мне впервые показал Джеймс Рэнди, который эффективно использовал его в своей магии. В нем волшебник предсказывает сумму четырех случайно выбранных трехзначных чисел.
Чтобы подготовить такой фокус, понадобятся три колоды из девяти карт каждая и лист бумаги с записанным числом 2247, который вы запечатаете в конверт. Далее над каждым комплектом карт произведите следующие действия.
На колоде А запишите такие цифры (одно на каждую карту):
4286 5771 9083 6518 2396 6860 2909 5546 8174
На колоде Б запишите числа:
5792 6881 7547 3299 7187 6557 7097 5288 6548
На колоде В запишите следующие числа:
2708 5435 6812 7343 1286 5237 6470 8234 5129
Выберите троих человек из аудитории и вручите им по колоде карт. Пусть каждый из них наугад вытащит оттуда одну карту. Допустим, это карты с числами 4286, 5792 и 5435. Теперь, соблюдая очередность, пусть каждый громко назовет одну из цифр четырехзначного числа: сначала человек А, потом человек Б и, наконец, человек В. Скажем, они назвали цифры 8, 9 и 5. Запишите их (получится число 895) и скажите: «Вы должны признать, что данное число — результат абсолютно случайного выбора и его нельзя заранее предсказать».
Далее пусть три человека назовут другие цифры своих карт. Скажем, 4, 5 и 3. Запишите 453 ниже числа 895. Затем повторите данную процедуру еще два раза для двух оставшихся чисел, получив в итоге четыре трехзначных числа, например:
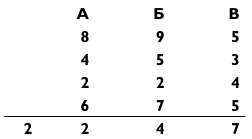
Затем пусть кто-нибудь сложит эти четыре числа и назовет сумму. А дальше пусть кто-то откроет конверт и покажет ваше предсказание. Теперь наслаждайтесь аплодисментами!
Почему это работает
Взгляните на числа на картах каждой колоды и подумайте, прослеживается ли в них какая-либо последовательность. Каждый набор чисел в сумме дает одинаковую величину. Сумма цифр каждого числа колоды А равна 20. Сумма цифр каждого числа колоды Б — 23. И сумма цифр каждого числа колоды В равна 17. Поскольку цифры из колоды В, которые в правом столбике, всегда в сумме дают 17, то в итоговой сумме в разряде единиц можно записать 7 и запомнить перенос 1 в следующий разряд.
Так как цифры из колоды Б в сумме дают 23, то в итоговой сумме в разряде десятков можно записать 4 (3 + 1) и запомнить перенос 2 в следующий разряд. Наконец, цифры из колоды А в сумме дают 20, поэтому после прибавления 2 получим итоговую сумму 2247!
ДЕНЬ ДЛЯ ЛЮБОЙ ДАТЫ
Мы завершим нашу книгу одним из проверенных временем подвигов ментальных вычислений — определением дня недели, на который приходится чей-либо день рождения. Это действительно очень практический навык. Вряд ли вас каждый день кто-то будет просить возвести в квадрат трехзначное число, но почти ни один день не проходит без того, чтобы кто-то не упоминал дату из прошлого или будущего. Всего лишь немного практики, и вы сможете быстро и легко определять день недели практически любой исторической даты.
Сначала присвоим кодовый номер каждому дню недели.
Их легко запомнить.

Далее нам понадобится код для каждого месяца. Эти коды применимы для любого года за исключением високосных. Для високосного года (например, 2000, 2004, 2008 и т. д.) кодом для января будет 5, а для февраля — 1.

Теперь вычислим день недели для любой даты в 2006 году.
После этого опишем 2007 год, затем 2008-й и т. д., до конца вашей жизни. Когда все даты из будущего будут определены, мы заглянем в прошлое и вычислим дни недели для любой даты из 1900-х или любого другого века.
Каждому году присвоен кодовый номер, и в случае 2006 года таковым будет 0 (см. таблицу ниже).
Чтобы вычислить день недели, нужно просто сложить код месяца, день месяца (дата) и код года. Таким образом, для 3 декабря 2006 года рассчитываем
Код месяца + Дата + Код года = 4 + 3 + 0 = 7.
Следовательно, эта дата приходится на 7-й день недели, то есть воскресенье.
Что вы скажете о 18 ноября 2006 года? Поскольку код ноября — 2, имеем:
Код месяца + Дата + Код года = 2 + 18 + 0 = 20.
Так как дни недели повторяются каждые семь дней, нужно от ответа (20) отнять любое кратное 7 (то есть 7, 14, 21, 28, 35, .), и это никак не повлияет на номер дня недели. Итак, заключительное действие сводится к вычитанию из полученной суммы наибольшего кратного 7. В данном случае получаем 20–14 = 6. Следовательно, 18 ноября 2006 года приходится на субботу.
Что можно сказать о 2007 годе? Точнее, что происходит с вашим днем рождения при переходе от одного года к следующему? Большинство годов состоят из 365 дней, а так как 365 = 7 х 52 + 1, то день недели вашего рождения сдвинется на один день вперед. Если между вашими днями рождения 366 дней, то день недели вашего рождения сдвинется на два дня вперед. Поэтому для 2007 года мы вычисляем день недели как и раньше, но применяем код года, равный 1. Далее следует 2008 год — високосный. (Високосный год бывает раз в четыре года, так что 2000, 2004, 2008, 2012… 2096 — високосные годы XXI века.) Поэтому для 2008 года его код увеличивается на два и равен 3. Следующий 2009 год не високосный, поэтому код увеличивается на 1 (и равен 4).
Таким образом, для 2 мая 2007 года, например, имеем:
Код месяца + Дата + Код года = 0 + 2 + 1 = 3.
Следовательно, данная дата приходится на среду.
Для 9 сентября 2008 года имеем:
Код месяца + Дата + Код года = 4 + 9 + 3 = 16.
Отнимая наибольшее кратное 7, получаем 16–14 = 2, значит, эта дата приходится на вторник.
Но для 16 января 2008 года, поскольку этот год високосный, код месяца январь будет равен 5, а не 6. Поэтому:
Код месяца + Дата + Код года = 5 + 16 + 3 = 24,
и, следовательно, нужная дата попадает на день 24–21 = 3, который является средой.
Мы перечислили все коды для каждого года XXI века в следующей таблице. Но вам не нужно запоминать ее. Можно устно посчитать код для любого года в промежутке от 2000 до 2099.
Для определения кода года 2000 + x берем частное х/4 (игнорируя остаток) и прибавляем его к х. Код года можно уменьшить путем вычитания из него кратного 7.
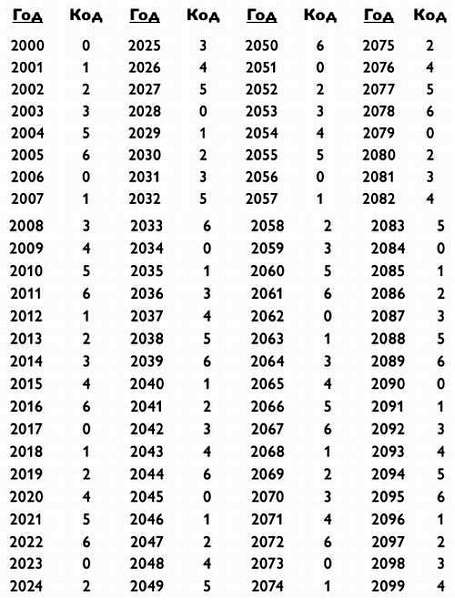
Например, для 2061 года имеем 61/4 = 15 (с остатком 1, который не учитывается). Тогда код 2061 года составит 61 + 15 = 76.
Или сокращенно 76–70 = 6.
Следовательно, для 19 марта 2061 получается:
Код месяца + Дата + Код года = 2 + 19 + 6 = 27.
Результат вычитания 27–21 = 6 говорит о том, что эта дата придется на субботу.
Что можно сказать о днях рождения между 1900 и 1999 годами? В этом случае задачу следует решать точно так же, как и предыдущие, но передвинуть итоговый ответ на один день вперед (или просто прибавить 1 к коду года). Тогда 19 марта 1961 года — это воскресенье.
Для даты 3 декабря 1998 года имеем 98/4 = 24 (с остатком 2, который не берем в расчет). Отсюда код 1998 года равен 98 + 24 + 1 = 123, где «плюс один» применяется ко всем номерам годов, больших 1900. Далее вычитаем наибольшее кратное 7.
Для удобства приведем числа, кратные 7, которые могут вам понадобиться:
7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126…
Так как 123–119 = 4, код 1998 года будет 4. Следовательно, для 3 декабря 1998 года имеем:
Код месяца + Дата + Код года = 5 + 16 + 3 = 24
и 11 — 7 = 4, так что эта дата приходится на четверг.
Для дат годов, больших 1800 и меньших 1900, нужно прибавлять 3 к коду соответствующего года из XXI века. Например, Чарльз Дарвин и Авраам Линкольн родились 12 февраля 1809 года. Так как код 2009 года — 4, то 1809-й будет иметь код 4 + 3 = 7, который можно сократить до нуля. Таким образом, для 12 февраля 1809 будет
Код месяца + Дата + Код года = 2 + 12 + 0 = 14
и 14–14 = 0, значит, оба родились в воскресенье.
Для дат 2100-х годов (то есть дат XXII столетия) следует прибавить 5 к коду соответствующего года XXI века (или вычесть из него 2, что эквивалентно). Например, код 2009 года равен 4, тогда 2109 год имеет код 4 + 5 = 9, который после вычитания 7 идентичен коду года 2.
Даты 1700-х годов (XVIII столетие) рассчитываются так же, как даты XXII века (путем прибавления 5 или вычитания 2), но здесь нужно быть внимательным. В то время был принят григорианский календарь, созданный в 1582 году. Но он не был официально принят англичанами (и американскими колониями) вплоть до 1752 года, когда среда 2 сентября вдруг стала четвергом 14 сентября. Удостоверимся, что 14 сентября 1752 года в самом деле было четвергом. Так как код 2052 года равен 2 (посмотрите в таблице выше или посчитайте 52 + 13–63 = 2), то 1752 год будет иметь код 0. Отсюда для 14 сентября 1752 года получаем:
Код месяца + Дата + Код года = 4 + 14 + 0 = 18
и 18–14 = 4, что действительно означает четверг. Однако наша формула не сработает для более ранних дат (которые исчислялись по юлианскому календарю)[18].
Наконец, отметим, что в соответствии с григорианским календарем високосный год наступает раз в четыре года, за исключением тех годов, которые делятся на 100, хотя есть и исключение из исключения: годы, делимые на 400, тоже являются високосными. Так, 1600, 2000, 2400 и 2800 годы будут високосными, а 1700, 1800, 1900, 2100, 2200, 2300 и 2500-й — нет. По сути, григорианский календарь повторяет себя каждые 400 лет, так что вы можете преобразовать любую дату из будущего в дату около 2000 года. Например, 19 марта 2361 года и 19 марта 2761 года придутся на тот же день недели, что и 19 марта 1961 года, которое мы ранее уже определили как воскресенье.
УПРАЖНЕНИЕ: ДЕНЬ ДЛЯ ЛЮБОЙ ДАТЫ
Определите день недели для следующих дат.
1. 19 января 2007 г.
2. 14 февраля 2012 г.
3. 20 июня 1993 г.
4. 1 сентября 1983 г.
5. 8 сентября 1954 г.
6. 19 ноября 1863 г.
7. 4 июля 1776 г.
8. 22 февраля 2222 г.
9. 31 июня 2468 г.
10. 1 января 2358 г.
Данный текст является ознакомительным фрагментом.