Глава 4 Теоремы Гёделя

Глава 4

Теоремы Гёделя

«Когда возникнет противоречие, необходимости в споре между двумя философами будет не более, чем между двумя математиками. Им будет достаточно взять перья и абак и сказать друг другу: произведем вычисления».

Готфрид Вильгельм Лейбниц

Улицы Кёнигсберга видели многое. В этом городе семь мостов, и жители не раз задавались вопросом: можно ли пройти по всем мостам ровно один раз и при этом вернуться в исходную точку? Этого не мог сделать никто, но и доказать, что это невозможно, также не удавалось, пока в 1735 году швейцарский математик Леонард Эйлер не создал теорию графов и не дал отрицательный ответ на этот вопрос.

Сорок лет спустя Иммануил Кант гулял по тем же мостам, пытаясь определить пределы чистого разума. Давид Гильберт также родился возле Кёнигсберга, и у общества сторонников эмпирической философии было достаточно причин, чтобы совместно с Венским кружком именно в этом городе провести конференцию с 5 по 7 сентября 1930 года.

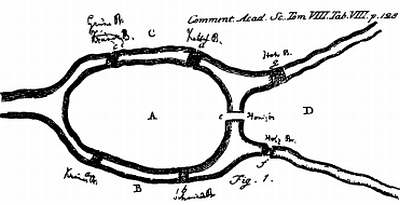
Схема решения задачи о кёнигсбергских мостах, принадлежащего Леонарду Эйлеру.

Целью конференции было определить, в какой степени в первые годы XX века удалось справиться с кризисом, вызванным парадоксом Рассела. Докладчиками на пленарном заседании стали те, кто внес наибольший вклад в развитие трех направлений, призванных разрешить кризис: логицизма, сторонники которого считали, что всю математику можно свести к логике; формализма, успехи которого заключались в проведении различий между языком и метаязыком; и интуицизма, в рамках которого предпринималась попытка исключить бесконечность из математики. Также в программу входили доклады участников, желавших представить свои последние открытия, и непринужденные беседы в городских кафе, которые, хотя и не могли сравниться с венскими, но тоже были весьма уютными.

Австрийский логик Курт Гёдель был приглашен выступить с тезисами своей докторской диссертации, открывавшей путь к математике, которой подвластно всё. Однако за то время, что прошло с момента защиты диссертации и до начала Кёнигсбергской конференции, Гёдель в своих исследованиях пришел к выводу, что мечте логиков его поколения не суждено сбыться. И хотя он не сказал об этом в своем выступлении, по окончании круглого стола, которым завершалась программа следующего дня конференции, он заявил, что располагает примерами истинных высказываний, которые нельзя доказать исходя из аксиом. Гёдель был подобен главному герою истории, который в финале произведения нашел разгадку с помощью ключа, упомянутого на первых страницах. Его слова застали собравшихся врасплох, поэтому практически не вызвали обсуждения и даже не были зафиксированы в протоколе.

Фотография Кёнигсбергского университета, известного в народе как Альбертина. Около 1900 года.

* * *

ДИАЛОГ ИЗ ФИЛЬМА «УБИЙСТВА В ОКСФОРДЕ»

(РЕЖИССЕР АЛЕКС ДЕ ЛА ИГЛЕСИА, АВТОР СЦЕНАРИЯ ХОРХЕ ГЕРРИКАЭЧЕВАРРИЯ, 2008)

Шелдон: О, я забыл, что говорю с защитником универсальной логики. Вы и полиция верите, что истину можно доказать. Исходя из неких аксиом с помощью корректных рассуждений можно прийти к верному выводу, не так ли?

Мартин: Это верно, как верно и то, что сегодня среда.

Шелдон: А что если я скажу «Все британцы лжецы»? Эта фраза будет истинной, ложной или ее нельзя будет доказать?

Мартин: Разумеется, существуют математические высказывания, которые нельзя доказать или опровергнуть исходя из аксиом. Это неразрешимые высказывания.

Шелдон: Именно. Теорема Гёделя о неполноте. Даже в мире чистой математики не все можно доказать.

Мартин: Да, я это знаю, но в нашем случае это не так.

Шелдон: Известно ли вам, что истинное и доказуемое разделяет пропасть, бездна? Мы никогда не узнаем, известны ли нам все данные о каком-либо явлении, при этом любая новая информация может изменить все.

* * *

И все же комментарий скромного юноши в круглых очках мог изменить направление дальнейшего развития всей логики, и это не ускользнуло от внимания некоторых присутствующих. Среди них был Джон фон Нейман, который, благодаря своей легендарной быстроте ума мгновенно понял, что имел в виду Гедель, и попросил его по окончании конференции изложить свои соображения подробнее. Фон Нейман учился с Гильбертом в Гёттингене и даже опубликовал несколько статей под его руководством, однако вскоре он начал сомневаться, что с помощью финитных методов, предложенных формалистами, можно доказать непротиворечивость математики. В юности фон Нейман добился некоторых успехов в разрешении этой проблемы и продолжал работать над ней. Как-то ночью ему приснилось решение, но, попытавшись его записать, математик увидел ошибку в рассуждениях и в итоге решил заняться другими вопросами.

Помимо открытий в области логики, Джон фон Нейман совершил важный вклад в квантовую механику.

Прибыв в Кёнигсберг в качестве приглашенной звезды, Джон фон Нейман вскоре понял, что его затмил актер второго плана, рассказавший о том, что именно могло присниться фон Нейману. Вернувшись домой, давний коллега Гильберта обнаружил, что если рассуждения австрийского математика верны, то непротиворечивость арифметики нельзя доказать в рамках самой арифметики. Фон Нейман сообщил об этом Гёделю 20 ноября 1930 года, всего через три дня после того, как Гёдель отправил в журнал Monatshefte fur Mathematik und Physik рукопись статьи «О формально неразрешимых предложениях Principia Mathematica и родственных систем I» с аналогичным выводом. Фон Нейман проникся уважением к своему коллеге, и когда весной 1931 года статья была опубликована, он прервал курс лекций в Берлине, чтобы объяснить важность открытия Гёделя, а 20 лет спустя вспоминал этот момент как «веху, видимую издалека, во времени и пространстве».

В дни проведения Кёнигсберской конференции в этом же городе находился и Давид Гильберт — он был приглашен на встречу общества немецких ученых, чтобы выступить с речью на тему «Логика и понимание природы». Эта речь прозвучала на следующий день после того, как Гёдель сделал свое заявление, и весьма вероятно, что он также находился среди ее слушателей. В своем выступлении Гильберт горячо провозгласил, что в математике не существует неразрешимых задач: «Не надо верить тем, кто сегодня с философической миной и тоном превосходства пророчит закат культуры, и впадать в ignorabimus[3]. Нет для нас, математиков, никакого ignorabimus, и, по моему убеждению, нет его и для естественных наук вообще.

Вместо дурацкого ignorabimus провозгласим наш контрлозунг: мы должны знать — мы будем знать!» Эхо выступления Гильберта еще не стихло, когда он узнал, что его программа находится под угрозой.

Теоремы о неполноте

До заявления Геделя программа Гильберта давала все основания рассчитывать на успех: ее первый этап, формализация математики, по всей видимости, был завершен Расселом и Уайтхедом в книге «Начала математики», а различные логики пытались доказать непротиворечивость классических формальных систем начиная с арифметики. Хотя еще во введении к своей докторской диссертации Гёдель предположил невозможность существования «истинных высказываний, которые нельзя вывести в рассматриваемой системе», он стремился не положить конец мечтам Гильберта, а доказать правильность его программы. Однако последние открытия того времени говорили об обратном: исследования Гаусса в области геометрии отрицали возможность создания идеально точной карты Земли; Эварист Галуа (1811–1832) доказал, что почти никакое алгебраическое уравнение нельзя решить простыми методами, а Вернер Гейзенберг (1901–1976) поставил новые задачи перед наукой, введя принцип неопределенности, согласно которому нельзя одновременно с точностью определить положение электронов и их скорость.

Теоремы Гёделя сделали очевидными все ограничения, присущие аксиоматическому методу: если в первой главе мы объясняли, что обязательными свойствами любой формальной системы являются непротиворечивость (полное отсутствие противоречий), рекурсивная перечислимость (возможность отделить аксиомы от прочих высказываний) и полнота (истинное и доказуемое полностью совпадают), то Гёдель показал, что арифметика не может обладать всеми тремя этими свойствами одновременно. Согласно его трудам, никакая рекурсивно перечислимая и непротиворечивая система аксиом арифметики не может быть полной, то есть всегда будут существовать какие-либо истинные свойства чисел, которые нельзя будет доказать исходя из аксиом арифметики. В этом и заключается суть теоремы Гёделя о неполноте, которую специалисты называют первой теоремой Геделя, так как, помимо нее, он доказал и вторую теорему, в которой утверждается, что высказывание «арифметика является непротиворечивой» являет собой пример неразрешимого высказывания. К таким же выводам по результатам конференции в Кёнигсберге пришел и фон Нейман.

Для доказательства первой теоремы о неполноте Гедель видоизменил парадокс лжеца, превратив его в неразрешимое высказывание, которое тем не менее не содержало противоречий. Очарование этой теоремы отчасти заключается в том, что она находится всего в одном шаге от парадоксов, но никогда не делает этот шаг. Мы уже рассказывали в главе 2 об антиномии Эпименида, которая в одной из формулировок звучит как «эта фраза ложна». И действительно, если это высказывание истинно, то оно само утверждает свою ложность, а если считать его ложным, то оно должно быть истинным. Что произойдет, если вместо истинных утверждений мы будем рассматривать доказуемые? Обозначим буквой G (по первой букве фамилии Геделя) высказывание «это высказывание недоказуемо» и будем предполагать, что используемая нами система аксиом является непротиворечивой. Если G ложно, то, так как G гласит «я недоказуемо», то G является доказуемым, однако в непротиворечивой системе никакое ложное высказывание не может быть доказуемым, так как это немедленно приведет к противоречию. Если С не является ложным, оно истинное, следовательно, имеем истинное высказывание, гласящее «я недоказуемо». Таким образом, мы предположили, что исходная система непротиворечива, однако обнаружили истинное, но недоказуемое высказывание. Иными словами, непротиворечивость подразумевает неполноту.

Мы предположили, что исходная система непротиворечива… Но какая система?

Внимательный читатель, задавшись этим вопросом и прочитав предыдущий абзац, возможно, подумал, что автор запутался и не совсем четко представляет, о какой системе идет речь. С удовольствием сообщаем, что читатель самостоятельно пришел к важнейшему вопросу, на который до Гёделя никто не мог дать ответ. Наши рассуждения показывают, что утверждение «я недоказуемо» должно быть истинным, однако здесь речь идет не о математическом высказывании, как нам бы того ни хотелось, но о метаматематическом, так как в нем говорится не об объектах изучения какой-либо теории, а о самой теории. Гениальность Геделя заключалась в том, что он перевел некоторые высказывания с метаязыка на язык арифметики благодаря системе кодов, в основе которой лежали простые числа. После этой «гёделизации» метаматематики натуральные числа стали вести двойную жизнь: с одной стороны, они остались неизменными, с другой — стали играть роль формул, что позволило выразить высказывание вида «я недоказуемо», которое априори имело смысл в метаязыке, в виде отношения между числами.

Более подробное описание гёделевской нумерации будет приведено дальше, а пока мы укажем, что с ее помощью в арифметике можно найти утверждение, эквивалентное высказыванию «я недоказуемо». Если бы множество аксиом арифметики S было рекурсивно перечислимым и непротиворечивым, то существовала бы истинная, но недоказуемая формула G_s (мы использовали индекс S, чтобы указать, что эта формула зависит от выбранных нами аксиом и при смене системы аксиом эта формула также изменится). Гёдель поставил всех логиков перед необходимостью сделать выбор либо в пользу полноты, либо в пользу непротиворечивости. И, что было еще хуже, арифметика была не просто неполной — ее полнота была недостижимой. Когда в начале этой книги мы приводили пример с инспектором полиции, который недавно пришел на службу, читатель мог возразить, что его коллеги наверняка узнали бы, женат ли он, продлись разговор немного дольше.

* * *

«ВСЁ, ЧТО НЕ В ВАШЕМ СПИСКЕ»

Рэндел Манро (род. в 1984 году) работал в NASA, пока в 2005 году не обнаружил в себе удивительный талант смешить людей шутками на околонаучные темы. Он начал рисовать комиксы xkcd — «веб-комикс о романтике, сарказме, математике и языке». В его схематичных комиксах часто упоминаются различные понятия физики, математики и информатики. Курт Гёдель становился героем множества историй, однако лучшая из них рассказана в комиксе «Фетиши», приведенном ниже. В нем вы можете видеть трех персонажей, а рисунки поясняет текст:

«Недавно писатель Катарина Гейтс попыталась составить таблицу всех сексуальных фетишей. Она понятия не имела, что ту же задумку уже однажды провалили Рассел и Уайтхед».

Один из героев комикса говорит:

— Привет, Гёдель. Мы тут собираем полный список всех фетишей. Скажи, что тебя возбуждает?

— Всё, что не в вашем списке, — отвечает Гёдель.

* * *

Существуют неполные системы, которые перестают быть таковыми, если добавить к ним несколько аксиом. Однако в случае с арифметикой это не так: Гёдель не только привел недоказуемое утверждение G_s, но и доказал, что не имеет смысла включать его в качестве аксиомы, так как, применив аналогичный метод на множестве Т = S + G_s  — множестве аксиом, которое вновь будет непротиворечивым и рекурсивно перечислимым, — мы получим новое истинное, но недоказуемое высказывание G_T. Если отрубить гидре с бесконечным числом голов одну, это не спасет нас от неполноты.

Мы обещали объяснить, как можно перевести на язык арифметики неразрешимое высказывание «я недоказуемо», однако вначале скажем несколько слов о второй теореме о неполноте. В главе 1 мы упомянули, что в противоречивой системе аксиом любое высказывание является теоремой. Следовательно, существование хотя бы одной формулы, которая не является теоремой, позволяет доказать, что рассматриваемая теория является непротиворечивой. Если можно найти всего одно недоказуемое высказывание, это автоматически доказывает непротиворечивость системы. Достаточно всего одного! Поэтому зачем рассматривать сложные высказывания, когда достаточно простейшего: 0 = 1? В начале книги мы указали, как теорема «единица отлична от нуля» выводится из аксиом Пеано. Нетрудно убедиться в том, что в любой разумной теории о числах, даже при выборе иных аксиом, ноль будет отличаться от единицы. Таким образом, заявление «арифметика является непротиворечивой» равносильно словам: формула 0 = 1 недоказуема.

И вновь мы столкнулись с высказыванием на метаязыке, однако благодаря «гёделизации» мы можем преобразовать ее в формулу о числах, которую обозначим Соn_S (где S — система аксиом). В этой системе обозначений первая теорема о неполноте гласит, что из Соn_S следует G_s так как если арифметика является непротиворечивой (иными словами, Соn_S истинна), то G_s истинна. Здесь будет уместно напомнить, в чем заключается одно из важнейших правил дедукции, modus ponens, позволяющее выводить из логической формулы «если А, то В» и формулы А формулу В. Предположим на мгновение, что непротиворечивость арифметики можно доказать в рамках самой арифметики. Следовательно, формула Соn_S является доказуемой, и, вкупе с доказательством первой теоремы о неполноте Соn_S —> G_s согласно modus ponens следует доказательство G_s. Однако этот вывод абсурден, ведь G_s недоказуема! Единственный возможный вывод таков: чтобы доказать непротиворечивость арифметики, нужно выйти за ее пределы — именно об этом говорится во второй теореме о неполноте, которую сам Гедель считал «неожиданным следствием» своих исследований.

Согласно программе Гильберта, для доказательства непротиворечивости математики следовало начать с арифметики. Тем не менее вторая теорема Гёделя указывает, что если доказательство непротиворечивости арифметики существует, то в нем обязательно должны использоваться более сложные методы, чем предложенные формалистами финитные. Читатель наверняка заметил, что название статьи Геделя «О формально неразрешимых предложениях Principia Mathematica и родственных систем I» наводит на мысли о возможном продолжении. И действительно, в этой статье содержались лишь наброски второй теоремы о неполноте. Хотя все указанное в ней было верно, Гедель так и не написал вторую часть статьи, что согласуется с его образом «исследователя, который оставляет работу над деталями остальным», созданным его биографами. На самом деле Гедель объяснил все подробности доказательства Давиду Гильберту и его коллеге Паулю Бернайсу (1888–1977) во время трансатлантического путешествия — они и опубликовали первое полное доказательство второй теоремы о неполноте в 1939 году. О духе тогдашней науки свидетельствует тот факт, что сам Гильберт завершил доказательство теоремы, которая сводила на нет все его труды в течение предыдущих 23 лет.

Однако теоремы о неполноте были приняты совершенно не так, как они того заслуживали. Некоторые математики считали, что неразрешимое высказывание «я недоказуемо» — лишь любопытный частный случай, никак не влияющий на их исследования. Были и те, кто не понимал тонкую разницу между истинным и доказуемым и обвинял Гёделя в том, что он воспроизвел парадокс лжеца. К их числу относился и шестидесятилетний Эрнст Цермело, хотя он как никто другой знал, сколь тяжело бороться за идею: его аксиома выбора в свое время вызвала огромное множество критических отзывов. Словом, математическое сообщество в то время не было готово понять работу, содержавшую принципиально новые методы и касавшуюся области, которая традиционно была уделом меньшинства. Томас Кун совершенно прав, указывая в своей книге «Структура научных революций», что «открытие всегда сопровождается трудностями, встречает сопротивление, утверждается вопреки основным принципам, на которых основано ожидание». К счастью, перевод статьи Гёделя на английский язык и популярное изложение его теорем способствовали тому, что начиная с 70-х годов теоремы о неполноте постепенно обрели статус важнейших открытий в логике со времен Аристотеля.

Курт Гёдель в Институте перспективных исследований в Принстоне, Нью-Джерси.

* * *

ГЁДЕЛЬ И АМЕРИКАНСКОЕ ГРАЖДАНСТВО

Покинув нацистскую Германию, Курт Гёдель в 1940 году был принят на работу в Принстонский университет. Когда семь лет спустя он получил американское гражданство, с ним произошел анекдотичный случай. Как и остальные кандидаты, Гёдель должен был продемонстрировать на экзамене знание американской конституции. И хотя экзамен был лишь формальностью, Гёдель решил серьезно подготовиться к нему, однако во время подготовки обнаружил в Конституции США несколько логических противоречий:

— Ранее у вас было немецкое гражданство?

— Нет, австрийское! — поправил чиновника Гёдель.

— Какая разница, в любом случае — страна с проклятым диктатором. К счастью, в Америке это невозможно!

— Совершенно наоборот, — перебил Гёдель. — И я знаю, как это может случиться!

Однако чиновник, которого Альберт Эйнштейн предупредил, что Гёдель отличается от остальных кандидатов, взял нить разговора в свои руки и перешел к рутинным вопросам, сказав: «Не будем умствовать». Примерно в то же самое время некоторые логики начали формировать основы новой теории — деонтической логики, целью которой было избежать противоречий при дополнении существующих законов новыми положениями.

* * *

Гёделевская нумерация

21 июня 1851 года Адольф Андерсен, лучший шахматист того времени, встретился в одном из старейших ресторанов Лондона с Лионелем Кизерицким, преподавателем шахматного клуба в Париже, и сыгранная ими партия позже была названа бессмертной. Впечатленный стратегией Андерсена, который пожертвовал слоном, ферзем и двумя ладьями, Кизерицкий захотел отправить запись партии в свой шахматный клуб. «Белые: пятая пешка слева передвинута на две клетки вперед. Черные: пешка на той же вертикали ставится перед пятой пешкой белых. Белые: третья пешка справа передвигается на две клетки вперед. Черные: пешка, которой был сделан первый ход, бьет пешку, которой белые совершили последний ход»… Но нет! Запись выглядела вовсе не так. Ее первые символы: е2—е4 е7—е5 f2—f4 е5: f4 …». Вся запись заняла не больше трех строк!

Если бы шахматист использовал первый способ записи, стоимость телеграммы с описанием партии превысила бы стоимость счета в «Кафе де ля Режанс», где сыграть в шахматы можно было за пять франков в час.

Игроки разработали чрезвычайно краткий способ записи ходов. Для этого они, во-первых, применили старинный метод аналитической геометрии Декарта, благодаря которому каждая клетка шахматной доски стала обозначаться двумя координатами: латинской буквой от а до h обозначались вертикали, числами от 1 до 8 — горизонтали. Пешки не обозначались никак, а все остальные фигуры получили обозначения по первым буквам названий (в русской нотации: Кр — король, Ф — ферзь, А — ладья, К — конь, С — слон). Далее нотация пополнилась другими символами: взятие фигуры обозначалось буквой х (в русской нотации — двоеточием), шах — знаком умножения в русской нотации и решеткой (#) — в международной. В этой нотации последовательность символов «е2—е4 е7—е5 f2—f4 е5: f4» означает: «белые делают ход пешкой на клетку е4, черные отвечают ходом пешки на е5. Затем белые делают ход пешкой на f4, черные проводят взятие этой пешки пешкой, которая находилась на клетке е5».

Этот пример подтверждает, насколько удобно использовать системы кодов в различных областях, в том числе за пределами математики, преобразуя сложные выражения в цепочку простых символов. В предыдущей главе вы видели, как свойства натуральных чисел, записанные обычным языком, можно перевести на язык символов, описанный в «Началах математики». Так, аксиома «0 не следует ни за каким натуральным числом» в этой системе преобразуется в формулу 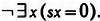  Однако Гёделю требовалось сделать еще один шаг вперед: чтобы доказать теорему о неполноте, ему было недостаточно свести арифметику к формулам — требовалось свести любую формулу и даже любое доказательство к единственному числу.

И Гёдель вспомнил, что на семинарах по истории философии, которые он посещал во время учебы в Венском университете, профессор Теодор Гомперц рассказывал об издании Луи Кутюром отредактированных рукописей Лейбница в 1903 году.

Подобно своим гениальным предшественникам, Лейбниц потратил немало сил, чтобы положить конец вавилонскому смешению языков, которым Бог наказал людей за то, что они хотели построить башню высотой до самого неба. Для этого Лейбниц задумал универсальный язык, в котором все человеческие мысли вне зависимости от языка носителя сводились к каталогу первичных идей, каждой из которых ставилось в соответствие простое число. С помощью этой системы можно было найти числа, соответствующие производным идеям так, что всегда было возможным «извлечь базовые обозначения, их составляющие», подобно тому, как из простых чисел образуются составные. Если понятиям «вода» и «неподвижность» поставлены в соответствие, например, числа 3 и 5, то понятие «озеро» (неподвижная вода) можно выразить произведением 3·5. И напротив, если понятие озера обозначается числом 15, мы можем разложить 15 на простые множители, найти в энциклопедии основных идей те, что соответствуют числам 3 и 5, и сделать вывод, что озеро есть не более чем неподвижная вода. Так, чтобы узнать, является ли утверждение вида «А есть В» истинным, достаточно определить, делится ли число, обозначающее В, на число, обозначающее А, и «когда возникнет противоречие, необходимости в споре между двумя философами будет не более, чем между двумя математиками». Эта амбициозная программа Лейбница, открытая спустя двести лет после его смерти, никогда не была реализована, однако она подсказала Гёделю, как можно перевести метаязык на язык арифметики.

Напомним, что простые числа — это числа, которые делятся только на 1 и на самих себя: например, число 5 простое, так как не делится ни на 2, ни на 3, ни на 4, однако 6 не является простым, так как при делении на 2 дает 3. Первыми простыми числами являются 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31. Путем доказательства от противного, которое так не любили интуиционисты, можно установить, что этот перечень простых чисел можно продолжать бесконечно. Большинство усилий физиков второй половины XX века было направлено на определение элементарных частиц, из которых состоит материя и которые нельзя разделить на другие, более мелкие частицы. Математикам же со времен Евклида известно, что элементарными частицами арифметики являются натуральные числа. Действительно, для любого натурального n возможны два варианта: либо n является простым, либо существует число, отличное от 1 и n, которое является делителем этого числа. Если, например, n равно 23, то мы имеем дело с первым случаем, но если n равно 30, то его можно разделить на 2.

Следовательно, исходное число не является простым. Его можно представить в виде произведения: n = а·b (в нашем случае 30 = 2·15). Мы получили два числа, для которых повторим вышеописанные действия: если оба этих числа являются простыми, процесс на этом завершается, но если одно из них не является простым, мы вновь запишем его в виде произведения сомножителей. В нашем примере 2 является простым, однако 15 можно представить в виде произведения 15 = 3·5, таким образом, 30 = 2·3·5. Так как 2, 3 и 5 — простые числа, процесс на этом завершается. В общем случае мы либо находим простой сомножитель, либо найденные нами множители постепенно уменьшаются — это гарантирует, что описанный нами процесс рано или поздно завершится. Таким образом, мы доказали основную теорему арифметики, которая гласит, что любое число можно представить в виде произведения простых множителей, которые могут повторяться. Пример: 77220 = 2·2·3 x 3·3·5·11·13. В этом случае используется сокращенная запись: 77 220 = 2²· З³ х 5·11·13, где показатели степеней указывают, сколько раз повторяется каждый сомножитель.

Основная теорема арифметики утверждает, что разложение на простые множители не только существует для любого натурального числа, но и является единственно возможным (порядок множителей при этом не имеет значения). Иными словами, мы можем записать число 77 220 другим способом, например 77 220 = 3· 2²·11 x З³·13, однако и в новом разложении будут использоваться те же простые множители, возведенные в те же степени.

В предыдущей главе мы показали, что «алфавит» арифметики состоит из восьми символов: 0 (число ноль), s (функция следования), ¬ (отрицание), V (дизъюнкция «или»), 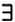 (существование), = (равенство), открывающие и закрывающие скобки.

Мы также использовали переменные х, у, z для обозначения чисел. На первом этапе кодификации Гёдель предложил поставить в соответствие каждому из этих символов число от 1 до 8, переменным х, у, z — три первых числа, больших 8, как показано в таблице ниже.

После того как мы присвоили числа «основным идеям» арифметики, закодировать формулу очень просто: сначала нужно подсчитать число используемых в ней символов (с повторениями) и выбрать столько же простых чисел. Размеры формулы не имеют значения, так как простых чисел бесконечно много. Далее каждое простое число возводится в степень, соответствующую символу, согласно таблице, приведенной выше, после чего все множители перемножаются. Но вместо долгих объяснений рассмотрим один пример.

Третья аксиома Пеано гласит, что «0 не следует ни за каким натуральным числом», и записывается в виде  Будем следовать инструкциям «гёделизации»: чтобы преобразовать эту формулу в число, сначала нужно подсчитать, сколько символов в ней используется. Их всего девять: ¬, , x, (, s, x, =, 0 и). Выберем первые девять простых чисел, а именно: 2, 3, 5, 7, 11, 13, 17, 19 и 23. Согласно таблице, ¬ отрицанию соответствует число 3, следовательно, нужно возвести простое число 2 в степень 3, то есть вычислить 2³. Квантор существования  обозначается числом 5, поэтому нужно возвести простое число 3 в пятую степень: 3⁵.

Повторив аналогичные действия, получим 5¹¹, 7⁷, 11², 13¹¹, 17⁶, 19¹ и 23⁸. После того как мы перемножим эти числа, формула примет вид:

2³·3⁵·5¹¹·7⁷·11²·13¹¹·17⁶·19¹·23⁸

Описанный нами метод позволяет представить любую формулу в виде числа, которое мы будем называть числом Гёделя. Никто не мешает нам выполнить аналогичные действия и для доказательств. Напомним, что доказательство — это не более чем конечная последовательность, состоящая, например, из п формул. Следовательно, можно сначала представить в виде числа каждую из этих формул, затем выбрать n простых чисел, возвести каждое из них в степень, равную числу Геделя для каждой из формул, после чего вычислить их произведение. Таким образом, любое арифметическое доказательство сводится к одному числу.

Ключевой момент здесь заключается в том, что «гёделизация» является обратимой. Те, кто немного знаком с химией, знают, что одной из важнейших задач в ней является определение того, какие реакции являются обратимыми. Например, при сжигании топлива оно превращается в водяной пар и диоксид углерода — знаменитый углекислый газ, являющийся причиной парникового эффекта. Однако из этих газов нельзя получить исходное топливо, в противном случае все энергетические проблемы человечества были бы решены. Другие химические реакции обратимы, как, например, реакция, происходящая при пропускании водяного пара над раскаленной железной пластиной: полученные в ее результате оксид железа и водород можно вновь превратить в железо и водяной пар.

Именно этот сценарий мы хотим восстановить в арифметике, так как числа никогда не смогли бы вести «двойную жизнь», как того хотел Гедель, если бы, играя одну роль, они навсегда забывали бы о другой. Благодаря основной теореме арифметики все «реакции» при «гёделизации» обратимы. Рассмотрим, почему это так.

Допустим, дано число

304 496 379 203 017 490 604 020 678 113 081 132 612 291 772 080 917 708 404 389 616 093 394 253 015 558 500 327 468 465 234 375 000,

которое мы записали специально для того, чтобы читатель представил себе наименьшие числа Гёделя. Основная теорема арифметики гарантирует, что это число можно разложить на простые множители. Если вы не хотите выполнять разложение вручную, что вполне объяснимо, то можете обратиться к веб-странице http://www.wolframalpha.com и записать в строке поиска слово «factor», а затем — это число.

Для разложения больших величин на простые множители компьютеру потребуется значительное время, однако важно другое: основная теорема арифметики гарантирует, что это разложение всегда существует и, более того, является единственным.

К счастью, наше число сравнительно невелико, поэтому его разложение на множители займет менее секунды:

2³·3⁵·5¹¹·7³·11⁵·13¹³·17⁷·19¹³·23⁶·29²·31¹¹·37⁸.

Теперь осталось внимательно рассмотреть показатели степеней и восстановить исходные символы согласно таблице. Мы получим формулу 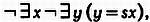 которая гласит, что не существует натурального числа х такого, что для него не существует числа у такого, что у является числом, следующим за х. Переформулировав это высказывание, читатель убедится, что его можно записать в виде «число, следующее за натуральным, тоже есть натуральное число», а это есть не что иное, как вторая аксиома Пеано.

Разумеется, не все натуральные числа являются числами Гёделя для какой-либо формулы, но даже если кто-то скажет нам, что какое-либо число не соответствует никакой формуле арифметики, мы мгновенно сможем это проверить. Например, 15 = 3·5 не является числом Геделя для какой-либо формулы, так как по условиям «гёделизации» разложение числа на простые множители должно обязательно содержать первые простые числа без пропусков, а в разложении 15 отсутствует число 2. Число 1536 = 2⁹·3 также не соответствует никакой формуле арифметики: хотя в его разложении присутствуют первые простые числа без пропусков, число 9 не соответствует ни одному из символов алфавита.

Подведем итог: описанная система кодификации позволяет сопоставить любой формуле (и любому доказательству) арифметики число, кодирующее всю ее структуру целиком. Кроме того, эта «математическая реакция» является обратимой в том смысле, что, разложив произвольное натуральное число N на простые множители, можно определить следующее.

1. Является ли N числом Гёделя для некоторой формулы.

2. Если число N соответствует некоторой формуле, то какой именно.

* * *

ГЁДЕЛЬ В ЛИТЕРАТУРЕ

В романе «Новые признания» (The new confessions) Уильяма Бойда главный герой снимает шедевр немого кино, однако его премьера остается незамеченной, так как в то же самое время появляются первые звуковые короткометражные фильмы. Лишь Курт Гёдель, который мимолетно появляется на страницах романа, признает талант режиссера.

В романе мексиканского писателя Хорхе Вольпи «В поисках Клингзора», опубликованном на десять лет позже, подруга главного героя, физика по имени Фрэнсис Бэкон, врывается на семинар Гёделя в Институте перспективных исследований и начинает кричать на него, обвиняя в неверности. Когда действие переносится в последние ряды аудитории, «профессор Гёдель объявляет, что не может продолжать занятия, и безудержно заливается слезами». Главным его конфликтом, объясняет автор устами фон Неймана, были не формально неразрешимые предложения, а «терзания от любви к проститутке — собственной жене». Эпизод «Новых признаний» выглядит правдоподобным, но сцена, описанная Вольпи, и жестока, и неправдоподобна.

Писатель Уильям Бойд сделал Курта Гёделя одним из героев своего романа «Новые признания».

* * *

Доказательство теорем о неполноте

Хотя мы уделили немало времени объяснениям гениального метода нумерации, на создание которого Гёделя вдохновили труды Лейбница, не следует забывать, что этот метод — лишь средство достижения цели: доказать, что в любой непротиворечивой и рекурсивно перечислимой системе аксиом существуют истинные, но недоказуемые высказывания. В начале этой главы мы указали, по какой схеме должно выполняться это доказательство: в парадоксе лжеца нужно заменить понятие истинности понятием доказуемости и получить самоотносимое утверждение, которое гласит: «я недоказуемо». Если противоречия не допускаются, то это утверждение должно быть истинным, следовательно, недоказуемым. Основная сложность, как мы уже указывали, заключается в том, чтобы найти арифметический эквивалент этого утверждения на метаязыке, в котором речь идет не о числах, а о математических теориях. Теперь в нашем распоряжении есть все необходимые методы, позволяющие это сделать. Далее мы попытаемся изложить важнейшие этапы доказательства Геделя максимально простым языком.

Нужно перевести на язык арифметики утверждение «я недоказуемо». Но что означает доказуемость утверждения в системе аксиом арифметики? Это означает, что существует доказательство, которое заканчивается нашим утверждением, то есть конечная последовательность формул, каждая из которых является либо аксиомой, либо получена из предыдущих формул с помощью правил вывода. Чтобы определить, является ли последовательность формул, которую мы обозначим Z, доказательством высказывания X, нужно показать, что Z строится по вышеуказанному правилу и что его последней формулой является именно X. Основная идея заключается в том, чтобы с помощью «гёделизации» сопоставить формулам X и Z числа Гёделя, которые мы будем обозначать строчными буквами х и z. Нам хотелось бы найти механизм D, который позволял бы для натуральных чисел х и z через определенное количество шагов дать ответ, является ли последовательность формул, соответствующая числу z, доказательством формулы с числом Гёделя х. Следовательно, высказывание D(х, z) будет истинным, если Z доказывает формулу X, и ложным — в противном случае.

Приведем простейший пример. Напомним, что число Гёделя для второй аксиомы Пеано равно

2³·3⁵·5¹¹·7³·11⁵·13¹³·17⁷·19¹³·23⁶·29²·31¹¹·37⁸.

Так как определяющее свойство аксиом гласит, что они являются доказательством самих себя, то если мы подставим вышеприведенное число вместо х и z в D(х, z), результат будет истинным: последовательность формул для числа Гёделя z, состоящая в этом случае лишь из второй аксиомы Пеано, является доказательством формулы, которой соответствует число х — это вновь вторая аксиома Пеано! Однако если мы введем в качестве значения z число 2³·3⁵·5¹¹·7⁷·11²·13¹¹·17⁶·19¹·23⁸, механизм D(х, z) выдаст результат «ложь», так как формула, соответствующая этому числу, не является доказательством второй аксиомы Пеано. Тот факт, что формула для числа Гёделя х доказуема, означает, что существует число z такое, что после довательность формул, соответствующая z, является доказательством формулы, связанной с х. Иными словами, существует z такое, что высказывание D(х, z) является истинным. Как следствие, формула z D(х, z), которую для краткости будем обозначать Dem (х), гласит, что формула, соответствующая числу Гёделя х, доказуема. Вкратце повторим вышеизложенное: если бы существовала формула D, то благодаря «гёделизации» все тонкости доказуемости высказываний можно было бы свести к простому отношению между натуральными числами х и z. Какая же теория рассматривает подобные отношения? Арифметика!

Читатель уже наверняка понял, что наиболее трудоемкая часть работы Гёделя состояла в том, чтобы доказать, что механизм, обладающий описанными выше свойствами, действительно существует. Для этого Гёделю потребовалось 46 этапов, которые мы опишем лишь вкратце. Допустим, что дано некоторое натуральное число z, кодирующее некую последовательность формул. По основной теореме арифметики мы можем разложить z на простые множители:

z = p^k1·p^k2·p^k3·…·р^kn.

Итак, мы разложили число z на простые множители, возведенные в различные степени. Так как z соответствует последовательности формул, то каждый показатель степени будет числом Гёделя для одной из этих формул. Таким образом, мы можем определить числа Гёделя для всех формул последовательности, которые обозначим

k₁, k₂, k₃… k_n.

Вновь повторим одно из основных утверждений этой книги: доказательство — это конечная последовательность формул, каждая из которых является либо аксиомой, либо получена из предыдущих формул с помощью правил вывода. Следовательно, нужно подтвердить следующее:

— первый шаг: последовательность формул с числами Гёделя k₁, k₂, k₃… k_n является доказательством, то есть каждому из этих чисел соответствует либо аксиома, либо высказывание, которое получено из предыдущих с помощью правил вывода;

— второй шаг: последняя формула последовательности — это формула, которую мы хотим доказать.

Начнем с последнего шага, который является наиболее простым: нам дана формула, которой соответствует число Гёделя х, и мы хотим узнать, оканчивается ли последовательность высказываний этой формулой, — простейшее требование, которое должно выполняться, если речь действительно идет о доказательстве. Вышеприведенные расчеты позволяют определить числа Гёделя для каждой формулы последовательности. Последней формуле соответствует число k_n, поэтому достаточно проверить, что числа х и k_n равны. Никто не усомнится в том, что проверить равенство чисел очень просто.

Теперь перейдем к первому этапу нашей гонки с препятствиями и рассмотрим формулы, которым соответствуют числа Гёделя k₁, k₂,… k_n . Именно здесь обязательно должно выполняться условие рекурсивной перечислимости системы аксиом арифметики — ранее это условие казалось не более чем причудой. Напомним, что множество аксиом S является рекурсивно перечислимым, когда за конечное число шагов можно показать, является некоторое высказывание аксиомой или нет. Следовательно, в нашем распоряжении находится формула А(х) (А — по первой букве слова «аксиома»), которая для любого числа х позволяет определить, является ли соответствующее ему высказывание аксиомой. Достаточно вычислить А(k₁), А(k₂)… А(k_n), и мы узнаем, какие из высказываний предполагаемого доказательства являются аксиомами. Первая формула, которой соответствует число Гёделя обязательно должна быть аксиомой, так как ей не предшествуют формулы, из которых ее можно было бы вывести. Следовательно, если результат А(k₁) случайно окажется ложным, дальнейшие действия не потребуются: z не является числом Гёделя, соответствующим доказательству. Предположим, что этого не произошло.

Некоторые из следующих формул, которым соответствуют числа k₂, k₃,… k_n  будут аксиомами, другие — нет. Для тех, что не являются аксиомами, нужно показать, что они выводятся из предыдущих высказываний по допустимым правилам вывода. В своей скрупулезно выполненной работе Гёдель доказывает, что для каждого правила вывода существует формула I, которая для первых s чисел k₁, k₂,… k_s возвращает результат «истина», если формула, обозначаемая числом Гёделя k_s, выводится из формул, обозначаемых числами Гёделя k₁, k₂,… k_s -1 (предшествующей формулы), по соответствующему правилу вывода. Например, I(k₁, k₂, k₃, k₄) будет истинной, если четвертая формула последовательности выводится из трех предыдущих по правилу вывода, обозначаемому формулой I. Таким образом, этот процесс можно выполнить для формул, которые не являются аксиомами, и если для каждой из них формула, обозначающая хотя бы одно из правил вывода, вернет значение «истина», то первый этап будет успешно завершен, и z будет числом Гёделя, обозначающим доказательство. Так как здесь нетрудно запутаться в технических деталях, выделим главное: нужно запомнить, что мы доказали существование процесса D(х, z), определяющего, является ли последовательность формул, обозначаемая числом z, доказательством высказывания, которому соответствует число Гёделя х.

Для этого достаточно выразить в виде отношений между числами правила, которым должно удовлетворять доказательство, что мы уже не раз повторили.

Отлично: в рамках арифметики мы сформулировали высказывание Dem (х), которое гласит: «формула, выражаемая числом Гёделя х, доказуема». Отрицанием этой формулы будет ¬ Dem (х), которая звучит так: «формула, выражаемая числом Гёделя х, недоказуема». Пока что все абсолютно понятно, но мы постепенно приближаемся к тому, чтобы совершить своеобразное сальто-мортале. Сначала следует напомнить, что высказывание «арифметика является непротиворечивой», которое фигурирует во второй теореме о неполноте, равносильно высказыванию «формула 0 = 1 недоказуема». Напомним также, что 1 является числом, следующим за нулем, то есть 1 = s0. Предлагаем читателю убедиться, что число Гёделя для формулы 0 = 1 равно 255150. Следовательно, высказывание ¬ Dem (255150), переведенное на язык арифметики, гласит, что «формула, обозначаемая числом Гёделя 255150, недоказуема», то есть «формула 0 = 1 недоказуема», что равносильно высказыванию «арифметика непротиворечива». Высказывание ¬ Dem (х) позволяет убить сразу двух зайцев.

Важность выражения ¬ Dem (х) заключается в том, что это уже не высказывание на повседневном языке, а арифметическая формула, в которой используются только символы 0, s, ¬, V, =, (, ) и некоторые переменные. Буквы «Dem» — это лишь сокращенный способ записи этого выражения, так как его полная запись очень сложна и занимает не одну страницу. Однако если мы захотим найти его полную запись, то сможем сделать это, используя исключительно символы алфавита арифметики. И ради этого мы потратили столько сил! У нас нет никаких сомнений, что теперь читатель знает, что нужно сделать всякий раз, когда ему встретится записанная в таком виде формула: ее нужно записать согласно гёделевской нумерации. Сопоставим выражению ¬ Dem (х) число Гёделя, которое обозначим d. Возможно, это число будет настолько большим, что во всем мире не хватит чернил, чтобы записать его, однако его размер совершенно не важен — главное, что это число будет конечным.

Вся структура высказывания «формула, обозначаемая числом Гёделя х, недоказуема», содержится в единственном числе d. Параметр х не фиксирован, он не равняется, например, 14 451937 500, а может принимать любые значения. Но если этот параметр может принимать любые значения, почему бы умышленно не принять х равным d? В этом случае мы получим высказывание ¬ Dem (d), которое гласит, что «формула, выражаемая числом Гёделя d, недоказуема», но так как d, в свою очередь, является числом Гёделя, обозначающим высказывание «формула, выражаемая числом Гёделя х, недоказуема», ¬ Dem (d) преобразуется в высказывание «формула „формула, выражаемая числом Геделя х, недоказуема" недоказуема». Нетрудно видеть, что это высказывание означает не что иное, как «я недоказуемо»[4].

* * *

НЕПОЛНОТА ЗАМОЩЕНИЙ

Замощение плоскости — это покрытие ее «облицовочной плиткой» определенной формы без промежутков и наложений. Исламское искусство содержит прекраснейшие образцы замощений, но они встречаются и в природе: так, пчелиные соты представляют собой оптимальное замощение плоскости шестиугольниками. Оно необязательно должно быть правильным: возможно, существуют другие, непериодические замощения, не обладающие какой-либо симметрией.

В 70-е годы логик Хао Ван (1921–1995) обнаружил, что если вопрос о замощении плоскости является неразрешимым в том же смысле, в каком нельзя ни доказать, ни опровергнуть высказывание «я недоказуемо», то подобные непериодические замощения плоскости существуют. Так как возможность существования подобных замощений показалась ему полностью абсурдной, он сделал вывод: этот вопрос обязательно должен быть разрешимым. Однако несколько лет спустя один из его студентов доказал, что, используя 20426 плиток разной формы, можно получить непериодическое замощение плоскости. Эта величина понемногу уменьшалась, и в итоге было найдено непериодическое замощение плоскости, состоящее всего из двух плиток разной формы.