Приложение Доказательства

Приложение

Доказательства

1. Доказательство основной теоремы арифметики

Теорема утверждает, что любое натуральное число, отличное от 1, может быть единственным способом выражено в виде произведения простых чисел. Сначала мы должны объяснить, почему единица не считается простым числом.

Существует несколько причин, но наиболее очевидным является тот факт, что для числа 1 теорема не имеет места, так как оно может быть разложено на множители несколькими способами:

1 = 1 х 1 = 1 х 1 х 1 = 1 х 1 х 1 х 1 = …

С этой оговоркой мы можем доказать теорему в два этапа. Сначала покажем, что число может быть представлено в виде произведения, а затем — что это можно сделать единственным способом.

Первую часть докажем методом от противного. Предположим, что n является наименьшим числом, которое не может быть разложено на простые множители. Мы знаем, что это число не 1, потому что мы исключили такую возможность в формулировке теоремы. Не может оно быть и простым числом, так как тогда бы оно раскладывалось только на себя. Таким образом, это число должно быть составным вида n = а х Ь, где а и Ь меньше, чем n. Но так как n — это наименьшее число, которое не может быть разложено на простые множители, значит, а и b могут быть разложены на простые множители, что дает разложение и для n. Таким образом, мы пришли к противоречию.

Вторая часть доказательства опирается на следующий результат.

Если р — простое число, на которое делится произведение множителей, то на р обязательно должен делиться один из этих множителей. (Этот результат может быть доказан с помощью соотношения Безу.) Предположим, что натуральное число, большее 1, может быть разложено на простые множители двумя способами, тогда мы возьмем простое число р из первого разложения. На это число должно обязательно делиться второе разложение и, следовательно, один из его множителей.

А так как этот множитель — тоже простое число, он должен быть равен р. Таким образом, мы нашли два одинаковых множителя в разных разложениях. Повторяя процесс для любого другого простого числа из первого разложения, мы докажем, что оба разложения содержат одинаковый набор простых множителей.

2. Доказательство малой теоремы Ферма

В терминах теории сравнений, как в пятой главе, теорема формулируется так: «Если р — простое число, то для любого натурального числа а, а^р  a (mod р)». Это равносильно тому, что а^р  — а делится на р.

Докажем теорему с помощью метода индукции. Другими словами, мы предположим, что это верно для некоторого натурального числа а, и затем покажем, что это также верно для числа а + 1.

Начнем с предположения, что а^р — а делится на р. Согласно биномиальному разложению Ньютона,

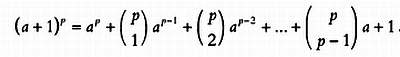
Перенося члены а^р и 1 налево, мы получим:

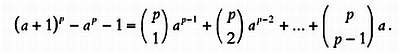
Множитель р содержится во всех слагаемых в правой части, поэтому правая часть уравнения делится на р и, следовательно, левая часть (а + 1)^р  — а^р — 1 тоже делится на р.

Так как по индукции а^р — а делится на р, то и следующая сумма также делится на р:

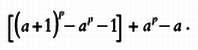
Эту сумму можно переписать в виде:

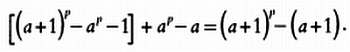
Следовательно, делимость на р верна и в случае а + 1, то есть теорема доказана.