Глава 2 Простые числа: ускользающие правила

Глава 2

Простые числа: ускользающие правила

Как мы уже говорили, простые числа представляют из себя одну из важных тем, которые возвращают нас к самым истокам математики, а затем по пути возрастающей сложности приводят на передний край современной науки. Таким образом, было бы очень полезно проследить увлекательную и сложную историю теории простых чисел: как именно она развивалась, как именно были собраны факты и истины, которые в настоящее время считаются общепринятыми. В этой главе мы увидим, как целые поколения математиков тщательно изучали натуральные числа в поисках правила, предсказывающего появление простых чисел, — правила, которое в процессе поиска становилось все более и более ускользающим. Мы также подробно рассмотрим исторический контекст: в каких условиях математики работали и в какой степени в их работе применялись мистические и полурелигиозные практики, которые совсем не похожи на научные методы, используемые в наше время. Тем не менее медленно и с трудом, но была подготовлена почва для новых воззрений, вдохновлявших Ферма и Эйлера в XVII и XVIII вв. Эти теории мы подробно рассмотрим в следующей главе.

Гении по наследству

Как и в истории математики в целом, с великими открытиями в теории простых чисел связаны имена нескольких человек. Но эти математики не смогли бы достичь таких результатов без богатого наследия, оставленного предшествующими учеными: гении не появляются из ниоткуда. Поэтому мы не должны игнорировать ту систему воззрений, на которой это наследие было построено, а также культурные традиции, которые помогли добиться таких научных результатов.

В 1930 гг. специализированные книжные магазины начали продавать учебники математики ранее неизвестного автора Николя Бурбаки. Эти книги сразу завоевали определенный успех в математическом сообществе. Среди прочего они содержали первое хорошее изложение теории математического анализа.

Однако их цель заключалась не только в обеспечении рынка новыми учебниками, но и в объединении отдельных областей математики, например, алгебры и анализа, где царил хаос из-за огромного количества новых результатов, полученных за последние годы. Но многие были удивлены, узнав, что математика Николя Бурбаки никогда не существовало и что этот псевдоним выбрала для себя небольшая группа математиков, в числе которых были Анри Картан (1904–2008) и Андре Вейль (1906–1998), решившие из благих побуждений реконструировать математику.

Труды группы Бурбаки хорошо документированы, потому что этот математический коллектив существовал совсем недавно. Но то же самое нельзя сказать о других школах древности, таких как школы Пифагора и Евклида: их работы сегодня приписываются одному человеку. Правда, многие полагают столь же вероятным, что эти труды были результатом сотрудничества нескольких человек.

* * *

ГЕНЕРАЛ-МАТЕМАТИК

Откуда взялся псевдоним «Бурбаки»? По версии одного из самых выдающихся членов группы, Андре Вейля, в его студенческие годы произошел такой забавный случай. Как-то раз Картан и Вейль посетили лекцию, которую читал странного вида математик с непроизносимым скандинавским именем и с неопределенным акцентом. Он рассказал об удивительной и невероятной теореме Бурбаки, автором которой был французский генерал Шарль Дени Бурбаки (1816–1897), знаменитый герой франко-прусской войны. Лекция оказалась шуткой другого студента, Рауля Хасона, но Картана и Вейля вдохновило имя генерала: греческое происхождение имени делало его идеальным псевдонимом, под которым можно было опубликовать «евклидову реконструкцию» математики. Так Бурбаки и стал великим математиком.

Генерал Дени Бурбаки, вдохновлявший патриотов и математиков.

* * *

Информационные центры

Замечательный факт состоит в том, что достижения в области научного знания, как в целом, так и в математике, никогда не зависят лишь от одного человека. Это правда, что некоторые люди совершают великие открытия, но они сами являются продуктом математического сообщества. Для нового открытия также необходимо, чтобы существовали журналы, читались лекции, проводились конференции, на которых может быть получена новая информация и установлены связи между учеными. В настоящее время, конечно, обмен информацией достиг беспрецедентного пика эффективности. Благодаря общению через интернет научное открытие оказывается в пределах досягаемости каждого, кто только пожелает получить к нему доступ. Однако потребность в сохранении информации (чтобы ею могли воспользоваться другие) существовала во все времена: это одна из культурных связей, объединяющих общество. В этом смысле простые числа являются необычным предметом исследования. Еще на заре истории они привлекали внимание исследователей и продолжают это делать до сих пор. Проследив историю этих исследований, мы не только получим информацию об их математической природе, но и сможем развивать такие точки соприкосновения, которые с использованием современной терминологии можно было бы назвать «информационными центрами». Александрийская библиотека является классическим примером одного из них.

Александрия

Птолемей I, известный также как Сотер («Спаситель»), был первым правителем Александрии. Привлекая лучших архитекторов мира, город превратился в архитектурное чудо. Длинная дамба соединила город с островом Фарос, на котором был построен маяк, указывающий путь средиземноморским морякам в течение тысяч лет. Затем была создана библиотека, слава которой сохраняется на протяжении всей истории человечества. Маяк и библиотека сделали Александрию одним из самых важных информационных центров древнего мира; этой цели Птолемей хотел добиться любой ценой. Его первым шагом было возвращение из ссылки тирана Деметрия, которого Кассандр, один из трех наследников Александра Великого, назначил правителем Афин. Именно Деметрий поддерживал работу лицея, основанного Аристотелем. Несмотря на политическую деятельность, истинным призванием Деметрия была наука, и поэтому он был рад получить приглашение Птолемея основать библиотеку в Александрии, в которой были бы собраны и систематизированы все знания цивилизованного мира.

Гавань Александрии состояла из небольших островов, защищенных дамбами, с единственным выходом к морю через большой канал, по которому могли входить и выходить корабли. Это надежно защищало гавань от атак с моря. Одним из самых важных районов был Брухеион, расположенный прямо в центре города, где находились наиболее важные общественные здания, в том числе музей, посвященный музам музыки и науки, то есть мелодиям, ритмам и цифрам. Когда Деметрий узнал, что этот центр знаний находится под покровительством одного из самых могущественных правителей в мире, он, не колеблясь, согласился стать его директором.

Первым делом он попросил у Афин рукописи наиболее выдающихся мыслителей и писателей Древней Эллады. Он приказал скопировать рукописи, вернул Афинам копии и оставил на хранение оригиналы вместе с текстами, которые Птолемей захватил в качестве трофеев во время военных кампаний.

Такой метод пополнения библиотеки оказался весьма эффективным, хотя и довольно неортодоксальным: все оригинальные документы, с которыми суда входили в гавань Александрии, реквизировались, копировались, оригиналы помещались в библиотеку, а копии возвращались владельцам. Именно так возникла так называемая «корабельная библиотека». Но вскоре богатые купцы Средиземноморья узнали об этой хитрости и отказались привозить рукописи. Тогда Деметрий сделал торговцам такое предложение: если они хотят торговать на рынках в порту Александрии, они должны привозить из своих городов рукописи в качестве пропуска в порт Александрии. Не имело значения, какие вопросы рассматривались в этих документах: техника, философия, искусство, математика или музыка, лишь бы они способствовали накоплению знаний. Идея заключалась в том, что с текстов будут сняты копии: оригиналы останутся в библиотеке, а копии будут возвращены торговцам. Эти копии возвращались владельцам в оригинальных переплетах, так что большинство торговцев даже не замечали разницы, а если и замечали, многих из них это не слишком беспокоило. Известно, что в то время Александрия содержала крупнейший в мире штат переписчиков книг.

Но Александрия была не только центром хранения информации: город стал местом, где информация обрабатывалась. Александрия быстро привлекла многих специалистов по всем дисциплинам, которые давали лекции и делились знаниями с другими учеными. Для этих целей строились учебные комнаты, жилье, галереи и парки.

Логично предположить, что появились научные школы, в том числе школа Евклида, которая, как и группа Бурбаки два тысячелетия спустя, собирала математические знания того времени и превратилась в учение, или, другими словами, в систему математических понятий и методов, достижения которой актуальны и сегодня.

Заметим, что две тысячи лет спустя в современной средней школе преподается та же геометрия, которая родилась в классных комнатах и садах древней Александрии.

Александрия была самым важным информационным центром древнего мира. На рисунке сверху: гравюра, изображающая ученых во время работы в знаменитой библиотеке. Внизу: римские монеты с изображением маяка на острове Фарос, еще одного чуда Александрии.

Большие пробелы

Одной из первых особенностей простых чисел, которая привлекла внимание древних математиков, было отсутствие правила, с помощью которого можно было бы предсказать их появление в последовательности натуральных чисел. Более того, даже их непоявление так же непредсказуемо. Они могут располагаться достаточно близко друг к другу или, наоборот, очень далеко друг от друга. Например, если взглянуть на простые числа из первой сотни натуральных чисел:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97,

становится понятно, что первые восемь простых чисел находятся в первых двух десятках, и ни одно не встречается между 89 и 97.

Ряд простых чисел второй сотни, между 100 и 200:

101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199

имеет большие пробелы: например, девять составных (не простых) чисел между 182 И 190.

Поэтому возникает вопрос: как такое возможно, что существуют очень большие пробелы, например, 50 000 идущих подряд чисел, среди которых нет ни одного простого числа?

Множество простых чисел достаточно большое, чтобы в нем могли встретиться сколь угодно длинные последовательности чисел, не содержащие ни одного простого числа. Этот вывод не просто гипотеза, его можно легко доказать.

Рассмотрим произведение первых четырех натуральных чисел:

1 х 2 х 3 х 4.

Мы можем быть уверены, что число 1 х 2 х З х 4 + 2 не является простым, так как оно делится на 2. Это можно сразу проверить: 1 х 2 х З х 4 + 2 = 26, и при делении на 2 мы получаем 13.

Но нам не нужно выполнять все вычисления, чтобы проверить делимость на два, так как оба слагаемых содержат множитель 2.

По той же причине очевидно, что число 1 х 2 х З х 4 + 3 = 27 не является простым, так как делится на 3; число 1 х 2 х З х 4 + 4 = 28 не является простым, так как делится на 4.

Таким образом, мы получили три последовательных числа, 26, 27 и 28, которые не являются простыми числами. Чтобы получить четыре последовательных составных числа, надо выполнить следующие действия:

1 x 2 x 3 x 4 x 5 + 2 = 122

1 x 2 x 3 x 4 x 5 + 3 = 123

1 x 2 x 3 x 4 x 5 + 4 = 124

1 x 2 x 3 x 4 x 5 + 5 = 125

Для краткой записи произведения последовательных чисел используется восклицательный знак:

1 x 2 x 3 x 4 = 4!

1 x 2 x 3 x 4 x 5 = 5!

В математике такое выражение называется «факториал». Например, факториал числа 6 равен

6! = 1 x 2 x 3 x 4 x 5 x 6 = 720.

Выражения для четырех последовательных составных чисел удобнее записать следующим образом:

5! + 2

5! + 3

5! + 4

5! + 5

Таким образом можно составить любой ряд последовательных чисел, не содержащий простых чисел. Например, если мы хотим получить сто последовательных составных чисел, достаточно написать:

101! + 2,

101! + 3,

101! + 4,

и так далее до 101! + 101.

Это означает, что в ряду натуральных чисел существуют промежутки любой длины, в которых нет простых чисел. Таким же образом мы могли бы построить ряд из пяти триллионов последовательных чисел, в котором простое число не появится.

Получается, что простые числа встречаются все реже по мере продвижения по ряду натуральных чисел, и, следовательно, при приближении к бесконечности наступит момент, когда простые числа больше не появятся.

Конечно, этот вывод неверен, так как мы знаем, что по теореме Евклида множество простых чисел бесконечно, и что каким бы длинным ни был ряд составных чисел, в конце концов появится простое число.

* * *

С ПОМОЩЬЮ КАЛЬКУЛЯТОРА

Хорошо бы использовать мощность компьютеров и написать программу, которая находила бы длинные ряды чисел, не содержащие простых чисел. В самом деле, алгоритм довольно прост, но нужно иметь в виду, что, работая с выражениями, содержащими факториалы, можно довольно быстро исчерпать память калькулятора. Факториалы будут расти с головокружительной быстротой. Это можно проверить на любом карманном калькуляторе, используя клавишу факториала (символ«!»). Посчитаем факториалы первых десяти чисел:

1! = 1; 2! = 2; 3! = 6; 4! = 24; 5! = 120; 6! = 720; 7! = 5040; 8! = 40320; 9! = 362880; 10! =3628800.

Большинство калькуляторов не смогут посчитать факториалы чисел, которые больше 70.

* * *

Чувство ритма

Во время концерта иногда возникает момент, когда публика оживляется и начинает аплодировать в такт музыке. Однако через некоторое время синхронность между ритмом хлопков аудитории и ритмом игры музыкантов нарушается. В случае простых ритмов синхронность может сохраняться довольно долго, но для более сложных ритмов это практически невозможно. Воспользуемся этой аналогией в отношении попыток математиков навязать чувство ритма простым числам, например, «один, два, три… вперед!» Но это не работает: простые числа не встречаются через каждые три составных числа. Попробуем по-другому: «один, два, три, двадцать, сто… вперед!» И это не работает. Мы могли бы повторять подобные попытки до бесконечности. Даже сегодня мы не знаем, подчиняются простые числа некоему чертовски сложному ритму или у них совсем нет чувства ритма.

Как найти закономерность в последовательности чисел? Для этого существует много способов. Важно, чтобы эта закономерность предсказывала появление следующего числа в последовательности. Например, для последовательности

2, 4, 6, 8, …

очевидно, следующее число будет 10.

В случае последовательности

1, 3, 5, 7, …

также легко предсказать, что следующее число — 9. Первый пример представляет собой последовательность четных чисел, а второй — нечетных. Еще один пример:

2, 3, 5, 9, 17….

Здесь каждое число получается умножением предыдущего на 2 и вычитанием из результата единицы.

Выражаясь языком математики, закономерность точно определена, если имеется «общий член» — выражение, позволяющее получить значение каждого члена последовательности, просто подставив значение индекса n. Например, для последовательности четных чисел формула общего члена выглядит так:

а_n = 2n.

Если n = 1, то а₁ = 2 х 1 = 2.

Если n = 2, то а₂  = 2 х 2 = 4.

Если n = 3, то а₃ = 2 х 3 = 6.

В случае последовательности нечетных чисел мы имеем следующую формулу общего члена:

а_n = 2n + 1.

Эту формулу можно использовать для нахождения значения любого члена. Например, чтобы найти значение члена, занимающего двадцать седьмую позицию в последовательности, мы подставим n = 27 в формулу общего члена:

а₂₇ = 2 х 27 + 1 = 55.

Нахождение формулы общего члена эквивалентно нахождению закономерности в данной последовательности. Возникает вопрос: поскольку мы можем найти любой член последовательности по формуле общего члена, можем ли мы найти эту формулу, имея достаточное количество членов последовательности? Для многих последовательностей ответ на этот вопрос часто является довольно сложной задачей.

Например, предсказать следующий член в последовательности

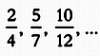
не так уж легко. И действительно, формула общего члена в данном случае выглядит так:

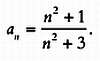
Чтобы найти первые три члена, подставим соответствующие значения n:

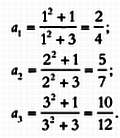
На протяжении многих веков это являлось одной из главных задач математиков в изучении простых чисел, но попытки найти закономерности и правила всегда заканчивались неудачей и разочарованием. Может, этот хаотический набор чисел действительно регулируется случайностью? Но математики, по-видимому, умеют ценить неудачи: пусть их усилия не достигают цели; даже в этом случае, возможно, будут найдены новые пути, разработаны другие математические методы или открыты новые понятия. Часто кажется, что поставленная цель была лишь предлогом для работы над новой задачей. Поэтому простые числа были и продолжают оставаться одним из самых богатых источников парадоксов и гипотез.

Простые числа-близнецы

Хотя общий закон для простых чисел нельзя установить, можно по крайней мере, изучать поведение некоторых простых чисел, имеющих особые свойства. Представьте себе, будто мы стоим у двери, через которую постоянно проходят группы людей. Мы знаем, что некоторые из них мужчины, а другие — женщины, но мы не можем найти правило, которое предсказывает, кто следующий появится в дверях.

И вот однажды мы замечаем некоторую особенность: оказывается, мужчины появляются в шляпах, а женщины в очках, с детьми и с зонтиками. Тогда мы пытаемся найти правило для каждой из таких групп: например, что мужчины в шляпах появляются в сто раз чаще, чем женщины, или что за каждым мужчиной обязательно следует женщина. Это позволяет нам найти некую закономерность. И может показаться, что такое правило действительно работает, пока мы не проверим его на трех миллионах человек. Тогда мы воскликнем: «О, почти!» И сформулируем результаты нашего исследования словами, которые часто использовались в истории простых чисел: «Похоже на то, что почти всегда…»

* * *

ОДИНОЧЕСТВО ПРОСТЫХ ЧИСЕЛ

Между двумя соседними простыми числами могут находиться миллионы и миллионы составных чисел или всего лишь одно, ведь это самое короткое расстояние между простыми числами, так как, за исключением чисел 2 и 3, простые числа никогда не следуют друг за другом. Этот факт был использован в виде метафоры в названии книги Паоло Джордано «Одиночество простых чисел». В одной из глав романа эта метафора описана более подробно: «В университете на одной из лекций Маттиа узнал, что среди простых чисел есть особенные. Математики называют их парными, или числами-близнецами. Это пары простых чисел, которые стоят рядом, то есть почти рядом, потому что между ними всегда оказывается другое число, которое мешает им по-настоящему соприкоснуться. Это, например, числа 11 и 13, 17 и 19, 41 и 43. Маттиа думал, что они с Аличе — вот такие простые числа-близнецы, одинокие и потерянные, вместе, но недостаточно близкие, чтобы по-настоящему соприкоснуться друг с другом».

* * *

Действительно, некоторые группы простых чисел удалось описать (в общей сложности несколько десятков), и это позволило добиться определенного прогресса.

Мы остановимся на некоторых необычных парах простых чисел, имеющих свойства, которые помогут нам лучше представить математические трудности, связанные с этим непредсказуемым множеством.

Два простых числа не могут идти друг за другом, так как каждое простое число является нечетным. Следовательно, между двумя из них должно быть четное число, которое не является простым. Таким образом, два простых числа всегда разделены по крайней мере одним числом. Исключение составляют числа 2 и 3, так как 2 является единственным четным простым числом.

В первой сотне натуральных чисел мы можем найти следующие пары чисел, отличающихся на две единицы:

(3, 3), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (39, 61) и (71, 73).

Такие простые числа называются «числами-близнецами» или просто «парными».

Парные числа могут быть описаны выражением (р, р + 2), где р — простое число. Ниже мы приводим список всех парных чисел из первой тысячи:

(3, 5), (5, 7), (11, 13), (17, 19), (29,31),

(41, 43), (59, 61), (71, 73), (101, 103), (107, 109),

(137, 139), (149, 151), (179, 181), (191, 193), (197, 199),

(227, 229), (239, 241), (269, 271), (281, 283), (311, 313),

(347, 349), (419, 421), (431, 433), (461, 463), (521, 523),

(369, 571), (599, 601), (617, 619), (641, 643), (659, 661),

(809, 811), (821, 823), (827, 829), (857, 859), (881, 883).

Мы знаем, что простые числа-близнецы по мере увеличения встречаются в ряду натуральных чисел все реже. Однако компьютерные вычисления показывают, что парные числа продолжают встречаться даже среди необыкновенно больших чисел.

А так как существует бесконечное количество простых чисел, можно выдвинуть гипотезу о существовании бесконечного множества чисел-близнецов, но это еще никому не удалось доказать.

Еще одна замечательная группа простых чисел, которая встречается в первой сотне натурального ряда, содержит три числа: 3, 5 и 7. Они могут быть записаны как (р, р + 2, р + 4), где р — простое число. Эта группа простых чисел состоит из так называемых «троек». На самом деле нет никакой необходимости давать им специальное название, так как существует только одна такая тройка. Это доказанный результат. К счастью, этот вопрос решен, в противном случае эта группа могла бы породить еще несколько недоказанных гипотез.

Самыми большими известными числами-близнецами (открытыми в 2009 г.) являются числа 65 516 468 355 х 2³³³³³³—1 и 65 516 468 355 х 2³³³³³³ + 1, каждое из которых состоит из 100 355 цифр!

* * *

БЕСКОНЕЧНЫЕ РАЗДЕЛЕНИЯ

Парные числа породили целый ряд гипотез в дополнение к той, согласно которой их множество бесконечно. Одна из них носит общий характер и была сформулирована в 1849 г. французским математиком Альфонсом де Полиньяком (1817–1890). Он предположил, что для любого числа С найдется бесконечное количество пар простых чисел, разделенных 2С составными числами.

Например, существует бесконечное множество простых чисел, разделенных четырьмя составными числами, шестью составными числами, восемью составными числами и так далее. При С = 1 эта гипотеза является гипотезой о бесконечном количестве чисел-близнецов.

* * *

Магия и математика

Мы уже говорили о той важной роли, которую информационные центры играют на протяжении всей истории науки. Сейчас мы остановимся еще на одном аспекте, который имел особое значение для истории математики, особенно для теории чисел: на связи магии и математики. Под магией мы подразумеваем историческую математическую традицию, называемую арифмологией или (чаще) нумерологией.

Связь между математикой и нумерологией аналогична связи между астрономией и астрологией или между химией и алхимией. В настоящее время эти пары практически не пересекаются, но на протяжении веков эти связи были достаточно прочны и не могут быть проигнорированы, если мы хотим понять, как развивалась каждая область в разные исторические периоды.

Числа, и в особенности простые числа, всегда были предметом не только математических, но и философских исследований, и даже элементами религиозных культов.

Являясь частью таких систем, они использовались по-разному. Они встречаются в Библии, в магических квадратах, в магических суммах и особенно в философии пифагорейской школы, для которой геометрические фигуры и цифры были основой всего сущего.

Поэтому имена таких известных математиков, как Мерсенн и Ферма, окружены тайнами и легендами. Владея самыми простыми математическими методами, они добились впечатляющих результатов, прославивших их на века. Французский математик и историк Аибри писал: «Ферма знал то, чего не знаем мы, и, чтобы повторить его результаты, нам требуются более совершенные методы, чем известные в его время». Кстати, в отличие от многих математиков того времени, Ферма не пытался скрывать свои знания, хотя и оставлял в тайне методы, с помощью которых он эти результаты получал.

В истории математики были такие периоды, когда математическая строгость, по сути родившаяся в XVIII в., не имела того значения, которое мы уделяем ей сегодня. В те времена математика была набором инструментов для практических целей, а не теоретической наукой. Таким образом, традиционный подход, проникнутый мистическим символизмом, не препятствовал развитию науки, а наоборот, давал простор воображению.

Таким образом, представление о математике может быть неверным из-за ошибочных представлений о том, как великие математики делали свое дело. Незнание того, как именно работают математики, ведет не только к непониманию природы математических исследований, но и в некоторой степени является причиной непопулярности этой науки. Конечный результат исследований, который обычно принимает форму теоремы, выглядит в переработанном и отшлифованном виде так, что почти всегда оказывается слишком непонятным для людей, не имеющих соответствующей подготовки.

Постороннему человеку трудно увидеть красоту в математических формулировках, которые содержат много технических деталей и чистой логики. Однако сам исследователь шел не по такому ясному и логичному пути, а долго блуждал в кромешной тьме в дремучем лесу чисел в поисках едва различимых тропинок.

* * *

КНИГА ЧИСЕЛ

«Числа» — это четвертая книга Библии и одна из частей Торы, содержащей Пятикнижие Моисея.

На первый взгляд, «Числа» является книгой счетов и, следовательно, представляет несомненную историческую ценность, так как в ней тщательно перечисляются все количества, от вождей племен до голов крупного рогатого скота, то есть книга служит историческим фоном для событий, описанных в других святых книгах. Однако «Числа» — это еще и книга секретных кодов для тех посвященных, кто может их расшифровать, потому что эти числа не только представляют собой количества, но и имеют особый смысл. Например, число 1 символизирует Бога, 2 — человека, 3 — совокупность вещей и так далее. Интересно, что число 5 представляет собой неопределенное количество, «несколько». Например, во время Нагорной проповеди при умножении хлебов Иисус взял пять хлебов, то есть «несколько хлебов». Особенность заключается в том, что число 5 является первым количеством, которое мы не можем определить с одного взгляда. Известно, что если группа содержит меньше пяти объектов, мы определяем их количество, фактически не считая их, а большие количества мы мысленно делим на группы по четыре предмета или меньше и затем складываем результаты.

Тора известна христианам как Пятикнижие и составляет первые пять книг Ветхого Завета.

* * *

Тот факт, что математика исследует самые тайные интеллектуальные ландшафты, беспокоил некоторых хранителей морали. Например, вот что говорил святой Августин: «Добрый христианин должен остерегаться математиков и всех прочих пустых предсказателей. Существует опасность того, что математики заключили договор с дьяволом, чтобы помрачить дух человеческий и увлечь его в ад».

В дополнение к тому, что мы называли информационными центрами и магическими аспектами чисел, есть еще один момент, на который следует обратить внимание при изучении истории теории простых чисел. Это исключительный дар в обращении с числами, которым обладают некоторые люди, — способность, в большинстве случаев сочетающаяся с исключительным даром слова. Многие известные математики, имена которых связаны с теорией простых чисел, также имели необычайные способности к языкам. Само по себе это не удивительно, ведь, как мы говорили в начале книги, цифры и слова связаны между собой как наиболее абстрактные понятия, используемые человеком. В ранние периоды, когда устройств, помогающих в вычислениях, практически не существовало, способность считать в уме являлась существенным преимуществом. Эта способность выходит далеко за рамки простых численных вычислений, ибо такое умение более подходит шоумену, чем математику.

Великие математики, такие как Ферма, Мерсенн, Эйлер и Рамануджан, обладали чудесным даром «видеть» мир чисел. Эта способность позволила им открыть такие связи, которые только они могли заметить. Но доказательство этих соотношений часто оставалось за пределами их возможностей, а иногда за пределами их интересов.

* * *

ЛЮДИ-КАЛЬКУЛЯТОРЫ

Люди-калькуляторы появились в XIX в. Для развлечения толпы они выполняли на сцене арифметические вычисления в уме. Вскоре они стали модными и выступали в европейских и американских театрах, привлекая зрителей своими удивительными способностями. Зера Колберн, один из первых профессиональных калькуляторов, история которого достоверно известна, родился в Каботе, штат Вермонт (США), в 1804 г. Однажды его попросили умножить 21734 на 543. Почти сразу же он дал ответ: 11801562. Когда кто-то из зала спросил его, как он это сделал, он ответил: «Я увидел, что 543 в три раза больше 181. Сначала я умножил 21734 на три, а затем умножил результат на 181». (Обычно ему требовалось всего несколько секунд для умножения пятизначных чисел.) Это произошло в 1812 г., когда Колберну было всего восемь лет.