Глава 1 Числа

Глава 1

Числа

Альберт! Перестань указывать Богу, что Ему делать!

Нильс Бор — Альберту Эйнштейну

Вначале были число и фигура. Когда человек попытался овладеть ими, родилась наука, и человек начал познавать окружающий мир. Развитие науки часто сопровождалось забавными, любопытными и даже анекдотичными случаями. Упомянуть их все или даже хотя бы самые известные из них — слишком обширная задача, так что мы остановились только на самых любопытных. Нашей единственной целью было показать читателю земную сторону математики, которую слишком часто считают наукой, недоступной простым смертным.

Великое изобретение

Паламед — персонаж древнегреческой мифологии, упоминаемый в легендах об Агамемноне и Ушссе — героях Троянской войны. Мы говорим о нем потому, что Платон иронично называет его создателем математики. По легенде, Паламед был создателем мер и весов, а также их концептуального выражения — числа. Он изобрел числа — что ни говори, не самое пустяковое открытие. Платон писал о предположительном существовании Паламеда с усмешкой: «Выходит, до того как Агамемнон поговорил с Паламедом, он не знал, сколько у него ног?» Непочтительный Платон был столь же острым на язык, как и его учитель, Сократ, которого даже приговорили к смерти за инакомыслие.

Цена истины

Древние греки считали, что если измерить величину а единицей измерения Ь, то дробь а/Ь будет мерой а. Иными словами, все, что можно измерить, имеет дробную меру, или, говоря современным языком, всякая мера эквивалентна рациональному числу и наоборот. К примеру, если отрезок имеет длину 70 см, а линейка — 20 см, то дробь 70/20 = 7/2 была мерой a, измеренной Ь. Так считали ученики пифагорейской школы. Но Гиппас из Метапонта (V век до н. э.) обнаружил, что измерить диагональ квадрата, выбрав в качестве меры его сторону, невозможно.

Подчеркиваем: не очень сложно, а именно невозможно.

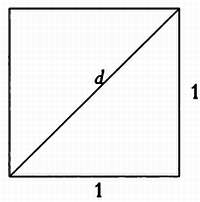
Диагональ квадрата несоизмерима с его стороной.

Если d = a/b, то очевидно, что мы можем выбрать а и Ь так, что они будут взаимно простыми. Достаточно сократить дробь а/b. Теперь рассмотрим самый простой случай — квадрат с единичной стороной. Теорема Пифагора гласит, что d² = 1² + 1² = 1 + 1 = 2, то есть (а/b)² = 2, или, если вы предпочитаете иной способ записи, а² = 2Ь².

Рассмотрим а подробнее. Если а четное, то b обязательно должно быть нечетным, так как мы предположили, что а и b взаимно простые. Так как а = 2р, предыдущее равенство примет вид (2р)² = 4р² = 2b², следовательно, 2р² = Ь², откуда следует, что b² (а следовательно, и Ь) четное. Но это невозможно, так как мы уже показали, что b должно быть нечетным.

Теперь предположим, что а нечетное. Тогда нечетным будет и a². Однако а² = 2Ь², и это означает, что а² четное, что противоречит нашей предпосылке. Как видите, получается нечто немыслимое, и первым это доказал пифагореец Гиппас.

Как известно, лучшее, что можно сделать, получив дурную весть, — это убить гонца. Ямвлих Халкидский восемь веков спустя утверждал, что пифагорейцы построили склеп, где должен будет упокоиться тот, кто откроет несоизмеримые величины. Существует несколько версий гибели Гиппаса. В самой милосердной версии он даже не упоминается и говорится лишь о том, что пифагорейцы принесли в жертву сто быков — столь велико было удивление, которое вызывали несоизмеримые величины. Так как пифагорейцы были вегетарианцами, эта гекатомба (что по-гречески и означает «сто быков») кажется возможной, но не слишком вероятной. В другой версии легенды Гиппас всего лишь был изгнан из пифагорейской школы. И в самом жестоком варианте он был сброшен в море с борта корабля. Как бы то ни было, вера пифагорейцев в истинность своего учения оставалась непоколебимой. Лишь Евдокс Книдский, открыв вещественные числа, смог разрешить загадку несоизмеримых величин.

Евангелисты, рыба и число 153

Одно из первых упоминаний о нумерологии в истории западной цивилизации содержится в 21-й главе Евангелия от Иоанна, где рассказывается о чуде в море Тивериадском, свидетелем которому стал Симон Петр, поймавший в сеть за один раз 153 рыбы. Разумеется, это чудо сотворил Иисус Христос.

Число 153 непременно должно обладать какими-то особыми свойствами. Действительно, это треугольное число. Читатель может сосчитать звездочки на рисунке и убедиться, что их действительно 153:

Однако этой причины недостаточно для упоминания в Евангелии. Рассмотрим равенства:

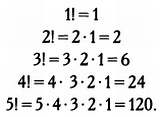
Мы видим, что 1! + 2! + 3! + 4! + 5! = 1 + 2 + 6 + 24 + 120 = 153, как показано на схеме:

Это уже лучше, однако и теперь найдутся неверующие, для которых и этой причины недостаточно, чтобы считать 153 божественным числом. В поисках лучше го решения будем действовать так: поскольку Бог един в трех лицах, рассмотрим любое число, кратное 3, например 1728, возведем все его цифры в третью степень и сложим их:

1³ + 7³ + 2³ + 8³ = 864

8³ + 6³ + 4³ = 792

7³ + 9³ + 2³ = 1080

1³ + 0³ + 8³ + 0³ = 513

5³ + 1³ + 3³ = 153

Удивительно, что ряд будет заканчиваться числом 153 для любого числа, кратного трем. Что это — чудо или занимательная математика?

Торговцы важнее математиков

Именно так считали в эпоху Возрождения. В 1456 году было изобретено книгопечатание, и путь к знаниям был открыт — для многих, но далеко не для всех, особенно если смотреть в прошлое из нашего благополучного XXI века. Вопреки ожиданиям, первой печатной книгой по математике были не «Начала» Евклида, подлинный памятник античной мудрости, а учебник по элементарной арифметике, отпечатанный в Тревизо под названием L’arte de l’abbacho («Искусство абака»). Автор книги ограничился объяснениями четырех арифметических действий и задачами о справедливом разделе вещей. Книга увидела свет в 1478 году. В ней использовались индоарабские цифры.

Купцы, которые интересовались подобными книгами, одержали верх над мудрецами и мыслителями. Впрочем, науке удалось отыграться: книга «Искусство абака» больше не переиздавалась, в то время как известно о сотнях изданий «Начал» Евклида.

Страница из учебника арифметики, отпечатанного в Тревизо, — первой в истории книги по математике.

Когда закончились буквы

Эта история, в которой сочетаются правда и вымысел, объясняет, почему в аналитической геометрии и в любых книгах по математике неизвестные чаще всего обозначаются буквой х. Начало этой традиции положил Рене Декарт (1596–1650) в своей книге «Геометрия», где обозначал известные числовые величины первыми буквами алфавита (a, b, с, d, …), а неизвестные — последними буквами (х, у, z). Так буква х, которая стоит на первом месте в этой троице, стала синонимом неизвестной величины.

Некоторые полагают, что инициатором такого решения был издатель книги: он заметил, что если литер с другими буквами не хватало, то литер с буквой х всегда было в избытке. Ее печатник и использовал при появлении неизвестной величины.

Как было на самом деле — мы уже не узнаем, но точно можно утверждать, что обозначение, введенное Декартом, сегодня использует весь мир.

Лейбниц и император Китая

Знакомство с двоичной системой счисления для разностороннего мыслителя Готфрида Вильгельма Лейбница (1646–1716) было сродни озарению. Царство единиц и нулей напоминало философский камень, способный превращать железо в золото: оно открывало новые, доселе невиданные горизонты. Единица (подобная Богу) и ноль (ничто) могли объяснить целую Вселенную, а простые 0 и 1 могли порождать любые числа. Это чудо следовало как-то объяснить и применить на практике.

В 1689 году Лейбниц обратился к своему другу, иезуиту Карлу-Филиппу Гримальди, главному придворному математику Китая (в последующие годы они вели весьма интересную переписку). Ученый просил Гримальди использовать все свое влияние и дар убеждения, чтобы, опираясь на новые знания о единице и нуле, убедить императора Кам-хи оставить буддизм и с распростертыми объятиями встретить христианство. Однако император Китая счел, что двоичная система никак не связана с единым Богом и вполне соответствует концепции инь и ян. Он не стал принимать христианство, а двоичная система счисления вернулась в царство арифметики, которое не должна была покидать.

Лейбниц упрямо приписывал полубожественные свойства всем новым математическим понятиям, о которых ему становилось известно. Например, таинственные мнимые числа он считал возвышенными и прекрасными, «амфибиями бытия с небытием».

Несносный ребенок

О детстве Карла Фридриха Гаусса (1777–1855), который был вундеркиндом, обычно рассказывают такую историю. Когда ему было 10 лет, учитель, желая немного передохнуть, дал Гауссу и его одноклассникам задачу, которая заняла бы детей надолго: нужно было найти сумму всех чисел от 1 до 100:

1 + 2 + 3 +… + 98 + 99 + 100.

Спустя несколько минут маленький Гаусс поднялся с места и протянул учителю грифельную доску с ответом: 5050. Как несносный ребенок смог так быстро справиться с задачей? Гаусс заметил, что если записать числа исходного ряда друг под другом справа налево и слева направо,

1 + 2 + 3 + … + 98 + 99 + 100

100 + 99 + 98 + … + 3 + 2 + 1,

то сумма чисел в каждой паре будет равна:

1 + 100 = 2 + 99 = 3 + 98 =… = 98 + 3 = 99 + 2 = 100 + 1 = 101.

Сколько всего таких пар? 100. Так как искомая сумма была в два раза меньше, ответ к задаче таков:

(100·101)/2 = 50·101 = 5050.

Обычно здесь и заканчивается легенда об одаренном ребенке с фантастическими способностями — наверное, для того, чтобы понять ее могли все, даже те, кто далеко отстал от Гаусса по своим способностям.

На самом же деле задача была еще сложнее: учитель предложил ученикам найти сумму первых 100 чисел ряда:

81297 + 81495 + 81693 + … —

каждое слагаемое отличалось от предыдущего на 198. Получить этот результат уже не так просто — выходит, Гаусс был еще умнее, чем гласит легенда.

Ферма и Куммер

В 1847 году французский математик Габриель Ламе (1795–1870) в присутствии множества коллег восторженно объявил, что доказал теорему, известную нам как великая теорема Ферма. При этом Ламе не преминул выразить благодарность вдохновившему его Жозефу Лиувиллю (1809–1882), который присутствовал здесь же.

По словам Ламе, без неоценимой помощи Лиувилля он не смог бы… и прочая, и прочая. В ответ совершенно пораженный Лиувилль обратил внимание собравшихся на одну небольшую деталь: доказательство Ламе было верно тогда и только тогда, когда выполнялось одно условие: целые числа определенного класса (далее мы определим их подробнее), как и обычные целые числа, можно разложить на множители единственным способом. Следует отметить, что в этом сомневались немногие. Ламе попытался найти доказательство для этого недостающего звена, но, к его разочарованию, сделать этого не удалось. Как сказал музыкальный критик об одном из произведений Дебюсси: «Его музыка не слишком шумна, но этот шум крайне неприятен». Ламе терял терпение, не в силах справиться с каким-то пустяком.

Тремя годами ранее немецкий математик Эрнст Куммер (1810–1893) опубликовал в малоизвестном журнале контрпример, в котором показал, что целые числа определенного класса можно разложить на множители не единственным способом. Узнав о попытках Ламе, Куммер поспешил отправить коллеге свой контрпример, и Ламе, лишившись надежды, оставил всякие попытки доказать теорему Ферма.

Сегодня известно, что знаменитые целые числа Ламе образуют так называемое квадратичное поле. Во времена ученого этим числам уделялось не слишком много внимания. Для обычных целых чисел, в частности на множестве 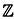, разложение на множители является единственным (если не делать разницы между 1 и —1). Например,

6 = 2·3 = 2·(—3)·(—1) = (—2)·3·(—1) = (—2)·(—3).

Множителями в этом разложении являются 2 и 3. На множестве  [?-5] (его элементы — числа вида a + ib?5, где а и b — целые), за исключением 1 и —1, разложить это число на множители можно уже не единственным способом:

6 = 2·3 = (1 + i?5)·(1 — i?5).

К примеру, целое число 6 (если принять, что 1 = —1) можно разложить на множители двумя разными способами.

Как говорится в пословице, нет худа без добра. Куммер начал охоту за доказательством теоремы Ферма, описав идеальные числа, и знаменитая недоказуемая теорема

Не существует тройки целых чисел х, у, z, которые удовлетворяли бы равенству хⁿ  + уⁿ = zⁿ для n > 2

была доказана для 100 первых показателей степени (ⁿ  < 100). Оставалось доказать ее для бесконечного множества чисел.

Эрнст Куммер.

Эрнст Куммер не только увлекался нумерологией, но также был ярым патриотом и славился неспособностью запомнить основы элементарной арифметики — обычные таблицы умножения. Когда ему нужно было использовать таблицу умножения в классе, он обращался к ученикам: «Семь на девять будет… эээ …» — тут какой-нибудь ученик, желая напакостить, обычно подсказывал неверный ответ: «Семь на девять будет шестьдесят один». «Нет, нет, шестьдесят девять», — подсказывал другой ученик, присоединяясь к общему веселью. И тогда бедному Куммеру не оставалось ничего другого, как невинно сказать: «Ну же, господа, давайте остановимся на чем-нибудь одном». Но правильный ответ был необходим, и Куммер начинал рассуждать логически. Сколько же будет 7·9? Числа 60, 62, 64, 66 и 68 не подходят, так как они четные, 61 и 67 не подходят, потому что они простые, 65 не подходит потому, что оканчивается на 5 и, следовательно, делится на 5. 69 тоже не подходит, так как очевидно, что оно слишком велико. Остается 63 — таким и должен быть ответ. Следовательно, 7·9 = 63.

1 + 1 = 2 и другие элементарные равенства

Немецкий математик Иоганн Петер Густав Лежён Дирихле (1805–1859) питал к числам особые чувства. Рассказывают, что даже ложась спать, он клал под подушку том «Арифметических исследований» Гаусса. А когда у Дирихле родился первый ребенок, он отправил тестю телеграмму:

2 + 1 = 3.

Яснее выразиться невозможно: раньше их было двое, и вот на свет появился третий. Кроме того, телеграммы в то время были очень дороги, так что послание Дирихле было не только лаконичным, но и дешевым. Он не первым и не последним использовал равенство, вынесенное в заголовок: сам Сократ ломал голову над выражением «1 + 1 = 2», будучи не в силах убедиться в его очевидности. Но что можно ожидать от человека, выбравшего своим девизом фразу «Я знаю только то, что ничего не знаю»?

Австрийский физик и математик Людвиг Больцман (1844–1906) как-то стал героем забавной сцены. Ученый умел быстро выполнять расчеты в уме, поэтому его занятия часто были настоящей пыткой для присутствующих: Больцман пропускал множество действий, так как считал очевидными вычисления, произведенные в уме, и даже не записывал их на доске. На одной из лекций его попросили все же расшифровать ход своих мыслей. Больцман покорно пообещал исправиться и продолжил рассуждения: «Как я уже говорил, поскольку pv = p₀v₀(1 + at) и так далее, и так далее», — однако по-прежнему ничего не записал. Закончил он свою непонятную лекцию бессмертной фразой: «Я верю, что все сказанное выше будет для вас столь же очевидным, как и то, что один плюс один равно двум». И тут, вспомнив о своем обещании записывать все вычисления, он подошел к девственно чистой доске и записал: «1 + 1 = 2».

Несколько позже Бертран Рассел (1872–1970) и Альфред Норт Уайтхед (1861–1947) удивили весь научный мир, создав на заре XX века (в 1910–1913 годах) невероятно сложный и почти недоступный для понимания трехтомный труд по логике, который, вслед за Ньютоном, назвали «Начала математики». Очевидное для непосвященных равенство «1 + 1 = 2», вынесенное в заголовок этой главы, во втором томе книги приводилось как теорема под номером 54.43, а весь первый том, можно сказать, подготавливал для него почву. Чтобы вы могли оценить всю «увлекательность» «Начал математики», приведем лишь один факт: редакция одной уважаемой газеты учредила премию для того, кто докажет, что прочел всю книгу. Премия так и осталась невостребованной. Какое-то время в редакции теплилась надежда, что хотя бы один из соавторов прочел книгу целиком, но эти ожидания были напрасными: и Уайтхед, и Рассел прочли только лично написанную часть труда.

Фрагмент «Начал математики», в котором приводится строгое доказательство равенства 1 + 1 = 2. Сначала, как иронично указано в тексте (здесь явно слышится шутливый тон Рассела), нужно определить операцию сложения.

Небольшие ошибки

Огюстен Луи Коши (1789–1857) как-то раз получил по почте объемный труд по теории чисел, в котором доказывалось, что диофантово уравнение

x³ + y³ + z³ = t³

не имеет целых решений. Коши, который отличался саркастичным и довольно насмешливым характером, отправил автору трактата письмо, состоявшее из одной строки:

3³ + 4³ + 5³ = 6³.

Нечто подобное произошло с прекрасным французским математиком Альфонсом де Полиньяком (1817–1890), известным сегодня как автор гипотезы о простых числах, представляющей собой обобщение гипотезы Гольдбаха. Полиньяк провозгласил:

Любое нечетное число можно представить как сумму степени двойки и простого числа.

Гипотеза не только впечатляла, но и выглядела вполне правдоподобно. Рассмотрим любое число, например 63:

63 = 2⁵ + 31.

Так как 31 простое, то, похоже, гипотеза Полиньяка верна. Прибавим еще один факт: Полиньяк дал понять, что проверил свою гипотезу для всех чисел вплоть до 3000000. Однако, видимо, в его вычисления вкралась ошибка: уже для числа 127 гипотеза не выполняется. Перечислим шесть первых степеней двойки и убедимся в том, что это и в самом деле так:

127 = 2¹ + 125 = 2¹ + 5·25;

127 = 2² + 123 = 2² + 3·41;

127 = 2³ + 119 = 2³ + 7·17;

127 = 2⁴ + 111 = 2⁴ + 3·37;

127 = 2⁵ + 95 = 2⁵ + 5·19;

127 = 2⁶ + 63 = 2⁶ + 3·21.

Однако следующей степенью двойки будет уже 2⁸ = 128 — число, большее 127. Таким образом, несмотря на заявления Полиньяка, его гипотеза не выполняется для числа 127.

Удивительные расчеты

Следующая история произошла на собрании Американского математического общества в октябре 1903 года. Математик Фрэнк Нельсон Коул (1861–1926) должен был выступить с докладом на тему «О разложении больших чисел на множители».

Выступление Коула было не совсем обычным: он поднялся с места, подошел к доске и записал на ней 2⁶⁷—1 — число Мерсенна М₆₇, которое считалось простым. Далее Коул вычислил значение 267 и вычел из него 1. Присутствующие затаили дыхание, а Коул записал на доске еще два числа и вычислил их произведение: 193707721 x 761838257287. Полученное число 147573952589676412927, как и ожидалось, было равно искомому числу М₆₇. Коул развернулся и проследовал на свое место.

Его доклад длился целый час, и за это время ученый не произнес ни слова. Однако аудитория все равно разразилась аплодисментами.

Следует отметить, что в 1903 году еще не существовало ни калькуляторов, ни алгоритмов, которые используются для работы с числами Мерсенна сегодня. По словам Коула, все необходимые расчеты он провел «за три года по воскресеньям».

В честь этого математического подвига Американское математическое общество учредило премию Коула, которая и сегодня остается очень престижной. За поиском простых чисел Мерсенна можно следить в интернете на сайте проекта Great Internet Mersenne Prime Search (http://www.mersenne.org/default.php). Самым большим простым числом, известным на февраль 2013 года, было М_57885161 — действительно большое число, состоящее из 17 425 170 цифр. И еще: М_5788М61 начинается с цифры 5. Больше об этом числе — ни слова.

Очень большое число

В математике можно говорить о сколь угодно больших числах — конечных, но очень больших, огромных, колоссальных. В 1938 году девятилетний племянник известного математика Эдварда Казнера (1878–1955) придумал число гугол, которое казалось ему невообразимо большим, практически бесконечным. Милтон Сиротта — так звали племянника — определил гугол как единицу, за которой следует 100 нулей.

В математической нотации это число записывается так:

1 гугол = 10¹⁰⁰.

Гугол кажется не слишком впечатляющим — куда больше впечатляет гуголплекс, определяемый как 1, за которым следует гугол нулей:

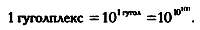
Долгие годы невинное изобретение Сиротты упоминалось в учебниках математики как любопытная диковинка, пока не появился Google. Этот компьютерный гигант был основан в 1998 году двумя молодыми американскими математиками — Ларри Пейджем (род. 1973) и Сергеем Брином (род. 1973). Сначала проектом компании был только поисковый механизм, который со временем занял важное место в интернете, а затем за ним последовали и другие проекты. Название компании представляет собой один из способов написать слово «гугол». На момент создания Google было проиндексировано всего 24 миллиона интернет-страниц, что достаточно далеко от обещанного гугола, но, как мы знаем, математикам часто присущ оптимизм.

Сага о числе 1729

Число 1729 считается мифическим благодаря известной истории о двух математиках — англичанине Годфри Харолде Харди (1877–1947) и индийце Сринивасе Рамануджане (1887–1920). Харди рассказывал, что как-то раз, навещая Рамануджана в больнице, он, чтобы завести с больным непринужденную беседу, сказал, что приехал на такси с номером 1729 — по словам Харди, это число было «ничем не примечательным». «Вовсе нет, — тут же ответил Рамануджан, — это наименьшее натуральное число, представимое в виде суммы кубов двумя различными способами». И действительно,

1729 = 12³ + 1³ = 9³ + 10³.

На доказательство этого утверждения, которое у Рамануджана родилось мгновенно, Харди потратил несколько недель. Позднее число 1729 дало начало целому подразделу теории чисел, который изучает так называемые числа Рамануджана — Харди.

Этот рассказ очень известен и подтвержден документально. Он позволяет понять, как работает ум гениального математика, каким Рамануджан, без сомнений, был. Однако не будем забывать о том, чем эта история закончилась, и здесь не обойтись без упоминаний еще об одном гении из мира математики и физики — о нобелевском лауреате Ричарде Фейнмане (1918–1988).

Как рассказывает сам Фейнман в книге «Вы, конечно, шутите, мистер Фейнман!», число 1729 помогло ему победить японского продавца счетов, который заявил, что может выполнять действия с числами быстрее всех. Убедившись, что чем сложнее становились вычисления, тем чаще Фейнман выигрывал, японец предложил ему задачу на извлечение кубических корней. Он попросил Фейнмана выбрать число, из которого нужно было извлечь кубический корень — и допустил промашку, потому что Фейнман сразу же выбрал 1729. Это число не вызвало у продавца подозрений, а

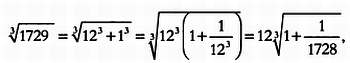
что можно с легкостью записать на бумаге и разложить в ряд Тейлора:

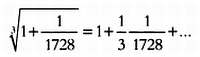
Этих членов уже достаточно для того, чтобы получить

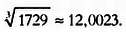
Фейнман тут же одержал над продавцом победу. Рамануджан, должно быть, с улыбкой смотрел на это с небес, из нирваны или любого другого места, где он сейчас находится.

Индийская марка, выпущенная в честь Сринивасы Рамануджана — величайшего математика в истории Индии.

Харди, Бог и гипотеза Римана

О выдающемся математике и писателе Годфри Харолде Харди рассказывают множество анекдотов, мы же приведем один из самых известных. Понять всю незаурядность Харди помогает список целей, составленный ученым. Наряду с довольно прозаичными пунктами в нем значилось следующее.

1. Доказать гипотезу Римана.

2. Набрать победное очко в важном крикетном матче.

3. Убить Муссолини.

4. Доказать, что Бога не существует.

О первом желании, с которым связан известный исторический анекдот, мы и расскажем. Однако вначале представим основных действующих лиц:

— Годфри Харолд Харди, прекрасный математик, известный прежде всего тем, что открыл для западного мира удивительного индийца Сринивасу Рамануджана;

— Бог, который не требует представления и которого Харди считал своим личным врагом;

— гипотеза Римана — несомненно, важнейшая гипотеза современной математики, которая по-прежнему остается недоказанной.

Изложим события согласно версии Дьёрдя Пойа (1887–1985), в которой можно оценить способности Харди и проследить за его математическими рассуждениями. Харди возвращался из Дании, где встретился с математиком Харальдом Бором, братом знаменитого физика Нильса Бора. Перед отплытием корабля в Англию погода испортилась, и вероятность того, что корабль попадет в шторм и потерпит крушение, была довольно высока. И тогда Харди отправил Бору открытку со словами: «Я доказал гипотезу Римана». Харди рассуждал следующим образом: если бы корабль утонул, то весь мир благодаря Бору узнал бы, что Харди доказал гипотезу Римана. Но Бог не мог допустить, чтобы его заклятый враг Харди обрел незаслуженную славу, поэтому он не дал бы кораблю утонуть. Таким образом, корабль не мог потерпеть крушение, что и требовалось доказать. Само собой, Харди по воле Бога добрался до Англии без происшествий.

Удивительно, но если путем Харди пойдет обычный человек, то он легко может допустить логическую ошибку. Так, часто рассказывают о некоем статистике, который вычислил вероятность того, что кто-то пронесет на борт самолета бомбу, и после этого стал каждый раз брать с собой в полет бомбу в чемодане. По его словам, вероятность присутствия на борту сразу двух взрывных устройств значительно меньше, чем вероятность присутствия одного. Разумеется, это вовсе не корректный статистический вывод, а обыкновенная наивность.

Очень похожую историю рассказывают о Давиде Гильберте (1862–1943), однако в ней речь идет о теореме (в то время — гипотезе) Ферма. Как-то раз Гильберт сообщил своим коллегам из далекого города, в котором он должен был вступить

Ноль и ничто

Во время интервью, которое выдающийся мыслитель Бертран Рассел дал индийскому писателю Разипураму Лаксману (род. 1924), словоохотливый Рассел заметил, что Индия не дала миру ничего: «You indians, have invented absolutely nothing» («Вклад индийцев в науку и культуру равен нулю») — сказал Рассел. Лаксман был ошеломлен: фраза показалась ему не просто невежливой — услышать ее из уст такого джентльмена было попросту немыслимо, к тому же она не соответствовала истине. Однако Лаксман не успел возразить: хитрый Рассел пояснил, что слово nothing, «ничто», следует понимать буквально. Nothing означает «ноль» — именно это имел в виду Рассел. Индийцы изобрели ноль — это и есть их важнейший вклад в науку.

Карикатура из газеты Evening Standard, опубликованная в 1961 году, когда Рассел в очередной раз был заключен в тюрьму за свои политические взгляды, противоречившие тогдашним законам.

Действительно ли все было именно так, доподлинно неизвестно. По всей видимости, стоит предполагать, что ноль изобрели именно индийские математики в VI веке. Они не только открыли способ описать «ничто», но добились значительно большего. Понятие нуля является одним из основных в позиционной системе счисления. Бертран Рассел был нобелевским лауреатом, одним из величайших математиков всех времен, но даже ему не удалось открыть хоть что-то, сопоставимое с нулем — изобретением столь же гениальным, как и колесо.

Удивительный гений

Гениальный венгерский математик Пал Эрдёш (1913–1996) был широко известен — отчасти благодаря экстравагантному характеру, о котором было сложено немало анекдотов, а отчасти — благодаря реальному вкладу в теорию чисел. Эрдёш и вправду был гением: он говорил, что открыл отрицательные числа, когда ему было всего 4 года.

Не рассказывать анекдотов об Эрдёше невозможно. Он, как и Харди, считал Бога своим личным врагом, который скрывает от людей прекраснейшие из теорем, а он, Эрдёш, должен вытягивать их из него силой. Математик утверждал, что самые примечательные образцы этой тайной мудрости изложены в воображаемой книге — сборнике шедевров мысли, и когда ему удавалось доказать какое-то очень красивое утверждение, он восклицал: «Это наверняка должно быть в книге!»

Эрдёш стал живой легендой, а некоторые математические понятия, связанные с ним, прочно вошли в науку, как, например, предложенное в шутку число Эрдёша, которое теперь изучается в теории графов. Число Эрдёша для любого ученого X определяется как наименьшее число Е(Х) такое, что для этого ученого найдется хотя бы один соавтор одной из его статей с числом Эрдёша Е(Х) — 1. Это рекурсивное определение заканчивается, когда мы определяем число Эрдёша, равное О, единственным обладателем которого является сам Эрдёш. Ученый имеет число Эрдёша, равное 1, если он написал статью в соавторстве с самим Эрдёшем. Очевидно, что число Эрдёша, равное 2, имеют те, кто написал статью в соавторстве не с Эрдёшем, а с одним из тех, кто имеет число Эрдёша, равное 1. Те, кто написал статью в соавторстве с ученым X, имеющим число Эрдёша Е(Х) = 2, имеют число Эрдёша, равное 3, и так далее. Тот, кто не связан с этой цепочкой соавторов, имеет бесконечно большое число Эрдёша. Число Эрдёша — это в высшей степени математический способ классификации математиков.

Множество математиков с числом Эрдёша, равным 1, содержит 311 человек. В их число входит знаменитый бейсболист Хэнк Аарон — по совету математика Карла Померанса (род. 1944) Эрдёш оставил ему автограф на бейсбольном мяче во время церемонии вручения степени почетного доктора. Кто-то подсчитал, что 90 % ученых современности имеют число Эрдёша, меньшее или равное 8. Наибольшее известное на сегодняшний день число Эрдёша равно 15. Следует отметить, что старейшим математиком, принадлежащим к этой блестящей компании, является Рихард Дедекинд (1831–1916) с числом Е (Дедекинда) = 7.

«Мой разум открыт» — говорил Пал Эрдёш друзьям, когда стучался в их двери, чтобы погостить у них. С собой ученый брал только чемодан и смену белья, поскольку все остальное — его ум и готовность решать самые запутанные задачи — были при нем всегда. После этой фразы часто звучало и другое его изречение: «Another roof, another proof» («Еще одна крыша, еще одно доказательство»).

Подсказка от Эрдёша

Все, что не было связано с математикой, вызывало у Эрдёша просто мучительную скуку. Как-то раз его пригласили на ужин, и когда ученый убедился, что гости действительно собрались ужинать, а не говорить о математике, то уткнулся носом в тарелку и заснул. Существует еще одна история, рассказанная польско-американским математиком Марком Кацом (1914–1984). Один из семинаров Каца был посвящен теме, не слишком интересной Эрдёшу, и тот благополучно задремал. Однако в какой-то момент Кац зашел в тупик, не в силах решить задачу о делителях числа, и ровно в этот же момент Эрдёш проснулся, словно хищник, почуявший добычу, и тут же погрузился в задачу. Кац еще не закончил говорить, как Эрдёш триумфально вскинул голову: задача была решена.

Числа господина Смита

Эта история началась благодаря Альберту Вилански, который описал новый класс чисел, взяв за основу телефон своего зятя — по крайней мере, именно так изложены события в книгах по теории чисел. У зятя Вилански, некого Гарольда Смита, был номер телефона 4937775. Сумма его цифр равна 42:

4 + 9 + 3 + 7 + 7 + 7 + 5 = 42.

Затем Вилански разложил номер телефона на простые множители:

4937 775 = 3·5²·65 837

и записал его без показателей степени, точно так же, как это делают школьники:

4937 775 = 3·5·5·65 837.

Сюрприз! Сумма всех цифр этих чисел вновь равнялась 42:

3 + 5 + 5 + 6 + 5 + 8 + 3 + 7 = 42.

Другой не обратил бы на это внимания, но Вилански испытал настоящее озарение. Так появились числа Смита. Число Смита (мы приведем его определение в десятичной системе счисления, но его можно определить и в любой другой) — это составное число, для которого при разложении на множители и записи в указанном виде сумма цифр исходного числа и сумма цифр его простых сомножителей равны. Изучение чисел Смита оказалось довольно плодотворным, и сегодня этим занимаются сотни и тысячи математиков. Известно, что чисел Смита бесконечно много (недаром это весьма распространенная фамилия в англоязычных странах), бесконечное множество из них является палиндромами, и даже известно одно любопытное число Смита

9·10₁₀₃₁(10⁴⁵⁹⁴ + 3·10²²⁹⁷ + 1)¹⁴⁷⁶·10^3913210,

где R₁₀₃₁ (R означает «репьюнит» от английского «повторяющаяся единица») обозначает целое число, записанное как 1031 единица подряд, или, что аналогично

R₁₀₃₁ = (10¹⁰³¹ - 9)/9

На 2010 год это число было наибольшим из известных чисел Смита. Самым примечательным в этом классе является «число зверя» 666, упоминаемое в Откровении Иоанна Богослова:

С другой стороны,

6 + 6 + 6 = 18.

666 = 2·3·3·37;

2 + 3 + 3 + 3 + 7 = 18.

Трепещите, каббалисты и приспешники темных сил! Жаль, что числа Смита имеют столь прозаическое название и обязаны своим появлением на свет телефонному номеру.

Муха

Американский физик и математик венгерского происхождения Джон фон Нейман (1903–1957) благодаря некоторым чертам своего характера также стал героем множества анекдотов. В одном из самых популярных рассказывается о его впечатляющих способностях к вычислениям и любопытной привычке действовать не так, как простые смертные. Задача о двух поездах и мухе стала уже классической, и звучит она так: предположим, что два поезда, А и В, отправляются навстречу друг другу из точек и В соответственно. Допустим, что расстояние между A и В равно 100 км, скорость поездов — 50 км/ч. В момент отправления муха, сидевшая на локомотиве поезда А, летит в точку В со скоростью 75 км/ч. Она летит быстрее, чем движется поезд А, и в конце концов встречается с поездом В. Достигнув поезда В, она сразу же поворачивает обратно и летит в сторону А. Когда она достигает поезда А, она вновь поворачивает обратно и летит в сторону поезда В, и так далее. Полет мухи закончится, когда оба поезда встретятся. Какое расстояние к этому времени пролетит муха? После трудоемких вычислений студент-отличник показал бы, что длина пути равна сумме следующей бесконечной геометрической прогрессии:

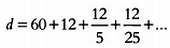
Знаменатель прогрессии равен 1/5, а ее сумма равна d = 75 км.

Проницательный неспециалист получит тот же результат, рассуждая следующим образом: поездам A и В встретятся в середине пути, на отметке в 50 км, время в пути составит один час. Следовательно, длительность полета мухи также равна одному часу, а поскольку скорость мухи равна 75 км/ч, то муха в сумме пролетит 75 км. Это решение элементарно, однако подойти к задаче подобным образом способны не все.

Когда один из коллег фон Неймана предложил ему эту задачу для развлечения, ученый незамедлительно дал ответ: «75 км». Коллега был несколько разочарован: «Ну вот, а я надеялся застать тебя врасплох. Ты очень умный, а вот большинство решает эту задачу с помощью суммы ряда». Фон Нейман с удивлением ответил: «А что я, по-твоему, сделал?» Гений среди гениев ни на секунду не задумался о другом решении. Он всего лишь вывел нужный ряд и мгновенно вычислил его сумму. Просто и быстро — если, конечно, вы — фон Нейман.

Западня Ферма

Некоторые известные задачи и простые математические темы попали на киноэкран: математике посвящены, в частности, фильмы «Маленький человек Тейт» (1991), «Куб» (1997), «Мёбиус» (1996), «Пи» (1998), «Энигма» (2001) и многие другие. Однако существует фильм, все действие в котором вращается вокруг математики, — это «Западня Ферма» (2007) режиссеров Луиса Пьедраиты и Родриго Сопеньи. В фильме снимается блестящий актерский ансамбль, а герой Алехо Саураса, молодой специалист с фамилией Галуа (подсказка для внимательного зрителя), играет особую роль — он нашел доказательство гипотезы Гольдбаха. К сожалению, доказательство было украдено, о чем сообщается в начале фильма.

Сюжет фильма полон неожиданных поворотов, один из которых (по всей видимости, он взят из рассказа Эдгара Аллана По) заключается в том, что герои фильма заперты в комнате со сдвигающимися стенами. Эта драматическая история — лишь сюжет фантастического фильма: еще никому не удалось достаточно близко подойти к доказательству гипотезы Гольдбаха. Галуа признает, что его доказательство было ошибочным, однако другой персонаж, по фамилии Гильберт (его роль исполняет Луис Омар), по всей видимости, находит корректное доказательство. К сожалению, Гильберт погибает, а его выкладки оказываются на дне реки. На сегодняшний день гипотеза Гольдбаха по-прежнему не доказана и ждет своего укротителя.