Глава 4 Все остальное

Глава 4

Все остальное

Статистика — это наука, доказывающая, что если у моего соседа две машины, а у меня — ни одной, то в среднем у каждого из нас по одной машине.

Бернард Шоу

Школьный курс математики охватывает только ее основы — арифметику, геометрию и начала алгебры и анализа. Казалось, что такой школьная программа будет всегда. Однако жить в нашем мире, ничего не зная о статистике, информатике и программировании, очень сложно. Неизвестно, что будут изучать в школах через 50 лет, однако школьная программа будущего наверняка будет отличаться от сегодняшней. Томази ди Лампедуза писал: все должно измениться, чтобы ничего не изменилось. Посмотрим, окажется ли он прав.

Далее мы расскажем о различных любопытных эпизодах из истории математики, которые не укладываются в рамки традиционных дисциплин. Мы поговорим о линейном программировании, астрофизике, гидродинамике, теории множеств и компьютерах. Откроем же двери в будущее.

Нос Тихо Браге

История была благосклонной к Тихо Браге (1546–1601), астроному выдающегося ума, высокомерному наблюдателю, который обладал прекрасным чувством юмора и располагал таким помощником, как Иоганн Кеплер (1571–1630). Страстью Тихо Браге было небо, а точность его наблюдений стала легендарной. Когда Кеплер спустя много лет заметил, что круговые орбиты планет не совсем точно описывают результаты наблюдений Браге, он предпочел поверить своему учителю, и оказался прав — его данные намного точнее описывались эллиптическими орбитами. Время подтвердило правоту Кеплера.

Когда Тихо Браге было 19 лет, он повздорил с юным и знатным дипломатом Мандерупом Парсбергом (1546–1625), о котором история не сохранила почти никаких сведений. Между ними разгорелся спор об эпициклах, обстановка накалилась, и дело закончилось дуэлью. На дуэли Парсберг разрубил Браге нос шпагой.

История гласит, что Браге повелел изготовить два искусственных носа: один из бронзы, другой (предположительно, для торжественных случаев) — из золота и серебра. Единственное неудобство заключалось в том, что когда Браге чихал, нос отваливался.

Тихо Браге не прекращал работать до самой смерти. Долгое время считалось, что он умер от заболевания почек, так как на одном из званых ужинов он выпил много вина, а протокол не позволил ему отлучиться в туалет. В 1996 году его останки были подвергнуты химическому анализу, и в них было обнаружено высокое содержание ртути. Тем не менее последующее исследование, проведенное в 2012 году специалистами из Орхусского университета, ставит версию об отравлении Тихо Браге под сомнение. Какова же истинная причина его смерти? Преступление?..

Прага, могила Тихо Браге.

Шифр Галилея

Вклад в современную науку Галилео Галилея (1564–1642) или Иоганна Кеплера не подлежит сомнениям, однако даже эти ученые порой ошибались. В частности, Галилей, наблюдая в 1610 году планету Сатурн в свой превосходный для того времени телескоп, обратил внимание на странные объекты рядом с Сатурном. Возможно ли, чтобы у планеты были уши? Или что это за «ручки» вокруг Сатурна? Быть может, это спутники? Позднее сам Галилей определил, что видел знаменитые кольца Сатурна.

Чтобы обеспечить себе первенство предполагаемого открытия, в письме Кеплеру Галилей сообщил о нем в зашифрованном виде (точнее говоря, используя логогриф), что было распространенной практикой в то время: логогрифы позволяли изложить мысль так, чтобы ее не понял непосвященный. Галилей написал Кеплеру:

smaismrmilmepoetaleumibunenugttauiras

Разумеется, Кеплер попытался расшифровать сообщение, расставив эту мешанину букв в правильном порядке. Потратив множество сил, Кеплер решил, что Галилей хотел сказать следующее:

Salve umbistineum geminatum Martia proles,

что в переводе приблизительно означает «Возрадуйтесь, два протуберанца, сыны Марса». Легко заметить, что расшифрованное сообщение на одну букву длиннее шифровки, однако Кеплер не придал этому значения, так как полученный текст соответствовал результатам его собственных наблюдений. Как и следовало ожидать (иначе не было бы этой истории), Кеплер расшифровал сообщение неверно. В действительности Галилей хотел сказать вот что:

Altissimum planetam tergeminum observavi.

В переводе это означает: «Я наблюдал, что самая высокая планета имеет форму цифры 3». Самой высокой планетой в то время назывался Сатурн. Между вариантами Кеплера и Галилея лежит пропасть, из чего следует, что каждый расшифровал сообщение так, как ему хотелось.

Многогранный космос

Астроном, математик и астролог Иоганн Кеплер был сыном своего времени и сочетал в себе мечтательность, способность к научным прозрениям и средневековую невежественность. Одной из самых странных и вместе с тем наиболее известных фантазий Кеплера была концепция, согласно которой на орбитах планет в зависимости от их размера построены вписанные и описанные правильные многогранники.

Кеплер развил эту идею в своей книге «Тайна мира». На ее иллюстрациях изображены правильные многоугольники, также называемые Платоновыми телами.

Эти фигуры, столь обожаемые Кеплером и подробно им изученные, были описаны еще Платоном в античные времена. Платон наделил правильные многогранники магическими свойствами: каждый многогранник с треугольными или квадратными гранями (тетраэдр, октаэдр, икосаэдр и гексаэдр, или куб) отождествлялся с одним из четырех основных элементов: землей, воздухом, огнем и водой. Додекаэдр — многогранник с двенадцатью пятиугольными гранями — отождествлялся с так называемой квинтэссенцией, веществом, из которого состояли небесные тела. Сегодня знаменитая квинтэссенция, или пятый элемент, осталась лишь в сказках, а додекаэдр считается всего лишь еще одним многогранником.

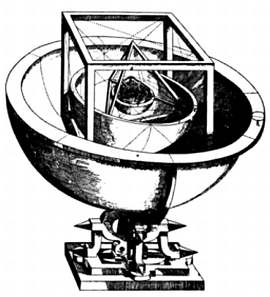
Однако в 2003 году была опубликована статья астрофизика (и — отчасти — мистика) Жан-Пьера Люмине (род. 1951), которая вновь пробудила интерес к додекаэдру. Данные, полученные спутником WMAP (Wilkinson Microwave Anisotropy Probe), по мнению Люмине и его группы, указывают, что пространство имеет положительную кривизну и с точки зрения топологии представляет собой додекаэдр Пуанкаре. В двухмерном пространстве (наши органы чувств воспринимают его как трехмерное) эту фигуру можно представить как сферу, поверхность которой вымощена двенадцатью пятиугольниками. Несколько лет спустя гипотеза Люмине была поставлена под сомнение, однако в остальном она не менее прекрасна, чем гипотеза Кеплера.

Статистик и лавочник

Ученые в большинстве своем сходятся во мнении, что основателем статистики является англичанин Джон Граунт (1620–1674). Каждое утро Граунт посвящал скрупулезной работе: он сводил в таблицы данные о смертности и причины смертей, которые каждую неделю брал у церковных служителей. Возможно, чтобы как-то скрасить мрачную картину, Граунт фиксировал и сведения о рождаемости. На основе частичных данных он получил более общие результаты. Славу британцу принесла брошюра под названием «Естественные и политические наблюдения над списками умерших» (Natural and Political Observations Made upon the Bills of Mortality), опубликованная в 1662 году.

Почему Граунт работал по утрам? Да потому, что он был простым лавочником и ежедневно должен был появляться в галантерейном магазине. То, что лавочник вел двойную жизнь, было настолько неслыханным, что его королевское величество Карл II даже издал указ, разрешавший торговцам впредь заниматься подобными делами, даже если они не вполне соответствуют их основному занятию. Граунт был избран членом Лондонского королевского общества в 1662 году — в тот же год, когда была опубликована его книга. Общество в то время было сравнительно немногочисленным и еще не страдало от бюрократии. Кроме того, немалую поддержку Граунту оказал королевский указ.

Невезучий астроном

Мы расскажем о Гийоме Жозефе Гиацинте Жан-Батисте Лежантиле (1725–1792), на долю которого выпало столь же много невзгод, сколь длинным и пышным было его имя. Не будем рассказывать о его злоключениях очень подробно: они слишком печальны и, кроме того, стали темой для пьесы и оперы.

Несчастья Лежантиля начались с попытки решить простую астрономическую задачу об измерении расстояния от Земли до Солнца на основе параллакса Венеры.

При наблюдении прохождения Венеры по диску Солнца из удаленных друг от друга точек земной поверхности можно увидеть, что относительное положение Венеры в зависимости от выбранных точек будет различаться, и это различие тем больше, чем дальше друг от друга располагаются наблюдатели. Примерно в 1760 году была организована группа для проведения необходимых наблюдений. Следует отметить, что из-за особенностей взаимного расположения планет транзит Венеры по диску Солнца наблюдается с интервалом, порой превышающим сто лет. Однако к наблюдателям XVIII столетия Бог был благосклонен, и Венера должна была пройти по диску Солнца дважды с интервалом в восемь лет.

Лежантиль, будучи патриотом Франции, выбрал для наблюдений самую удаленную от Европы французскую территорию — Пондишери в Индии. Он отправился в путь в 1760 году. К сожалению, политика внесла в его план коррективы: Франция и Англия начали войну, и Пондишери захватили британские войска.

После ряда перипетий Лежантиль решил ожидать прохождения Венеры по диску Солнца на острове Маврикий — французском анклаве в Индийском океане. Однако удача отвернулась от него: транзит Венеры произошел, когда корабль Лежантиля находился в открытом море, и произвести точные измерения было невозможно.

Следующее прохождение Венеры ожидалось через восемь лет. Лежантиль уже находился вдали от Франции и не видел смысла в том, чтобы вернуться домой. С Маврикия он отправился в Манилу, однако испанские власти отнеслись к нему недоброжелательно. К счастью, после заключения мирного договора Пондишери вновь оказался в руках французов, и Лежантиль направился туда. Там он построил обсерваторию и стал ждать транзита Венеры по диску Солнца. Стояла прекрасная погода, в том числе в день накануне события, однако в час X с самого рассвета небо заволокло тучами, и разглядеть сквозь них Солнце было невозможно. Восемь лет оказались потрачены впустую, и Лежантиль едва не сошел с ума.

Но и это еще не все — главные злоключения ученого были впереди: Лежантиль отправился на родину, по пути он переболел дизентерией и преодолел множество трудностей, а во Франции обнаружил, что объявлен мертвым, его имущество поделили наследники, он потерял престижное место в Академии наук, а жена вышла замуж за другого. Лежантилю пришлось потратить несколько лет на то, чтобы вернуть себе имущество и место в академии. К счастью, не подвергалось сомнению хотя бы то, что он действительно жив — возможно, потому, что король Людовик XVI принял участие в судьбе ученого и лично проследил, чтобы все его дела были улажены.

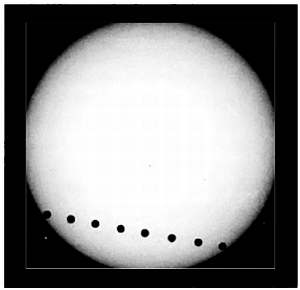
Прохождение Венеры по Диску Солнца, наблюдавшееся 8 июня 2004 года.

Статистика не врет

Такие писатели, как Александр Солженицын (1918–2008) или Хорхе Луис Борхес (1899–1986), довольно неплохо разбирались в математике, однако они представляют собой скорее исключение, чем правило. Впрочем, знакомство с элементарными понятиями необходимо каждому.

Известен случай с Чарльзом Диккенсом (1812–1870), который однажды в начале декабря отказался садиться в поезд. Он не имел ничего против железной дороги как таковой, однако в этот год число происшествий на ней было ниже обычного, и Диккенс ошибочно счел, что до конца года должно произойти сразу несколько аварий, чтобы «скомпенсировать отставание от графика». Ученый отказался ехать, не подумав, что в том году по счастливой случайности могло произойти меньше аварий, чем в предыдущем. Его вера в статистику была столь же непоколебимой, как вера великомучеников в Бога.

Если бы Федор Михайлович Достоевский хорошо разбирался в теории вероятностей, он никогда не стал бы игроманом, но и не написал бы роман «Игрок», а если бы голливудские сценаристы и режиссеры были знакомы с расчетом конструкций, то никогда не сняли бы фильм о Кинг-Конге. Так что лучше оставить все как есть.

Графиня-программист

Ада Августа Байрон (1815–1852), позднее — графиня Лавлейс, более известная как Ада Лавлейс, стала привлекательным персонажем для исторических хроник.

Во-первых, она была дочерью блистательного лорда Байрона, поэта и писателя-романтика, с которым, однако, не поддерживала отношений.

Во-вторых, ее семья была прекрасным примером неблагополучной семьи — родители Ады разошлись еще до рождения дочери. Кроме того, ее жизнь пришлась на расцвет викторианской эпохи с ее специфическими ценностями.

В-третьих, вопреки обычаям того времени, Аду обучали наукам — отчасти под влиянием матери, получившей математическое образование, отчасти для того, чтобы девочка не забивала себе голову отцовскими стихотворениями. В числе учителей Ады был блестящий математик Огастес де Морган.

В-четвертых, Ада Лавлейс была прекрасным математиком. Результатом ее дружбы с гениальным Чарльзом Бэббиджем стали важные открытия, удивительные для того времени. В ходе работы над механической вычислительной машиной Бэббиджа, так называемой аналитической машиной, Ада Лавлейс создала первую в истории компьютерную программу, записанную на перфокартах. Хотя машина Бэббиджа была готова лишь частично, программа Ады работала на ней корректно.

В-пятых, Ада Лавлейс жила бурной жизнью: помимо науки, она испытывала безмерную страсть к лошадям и скачкам, она делала ставки, завела роман с игроком и ей даже пришлось отдать семейные драгоценности в уплату его миллионных долгов.

Умерла Ада Лавлейс в возрасте 36 лет от рака матки. Ее смерть была долгой и мучительной. Мать Ады искренне беспокоилась за судьбу дочери на том свете и считала, что искупление грехов вечными муками следует начать еще при жизни, поэтому отказывалась давать ей морфин, веря, что невыносимые физические страдания очищают душу Ады и искупают ее грехи, в том числе пристрастие к азартным играм.

Мать также попыталась «привести в порядок» бумаги дочери после ее смерти, но Бэббидж, который был членом парламента и обладателем рыцарского звания, не допустил этого и сам распорядился всеми бумагами Ады Лавлейс и ее завещанием.

В 1970-е годы в компании Honeywell Bull был создан язык программирования ADA, названный в честь Ады Лавлейс, который используется до сих пор. Что ж, заслуженная дань уважения графине и программисту.

Ада Августа Байрон Кинг (фамилию Кинг носил ее муж), больше известная как Ада Лавлейс. Портрет кисти британской художницы Маргарет Карпентер.

Флоренс Найтингейл и статистика

Крымская война вдохновила многих писателей, вызывала жаркие споры, ожесточенные парламентские дискуссии и даже была запечатлена на большом экране, к примеру, в фильме «Атака легкой кавалерии» (1936), где Эррол Флинн скачет на коне навстречу своей славе. Несмотря на все ужасы войны, в ней были и светлые страницы: британское правительство отправило на фронт женщину по имени Флоренс Найтингейл (1820–1910), которая стала главной медицинской сестрой. Леди со светильником, как прозвали ее раненые солдаты, воочию увидела грязь, антисанитарию и ужасную обстановку в военных госпиталях и начала достойную уважения борьбу за реформу здравоохранения. После войны ее ожидало новое, намного более важное сражение на родине. Флоренс Найтингейл и на этот раз одержала победу, заручившись поддержкой королевы Виктории и премьер-министра лорда Палмерстона. Флоренс была женщиной, и общество неодобрительно относилось к ее увлечению математикой — ее преподавателем был сам Джеймс Джозеф Сильвестр — и особенно статистикой. Однако Найтингейл совершила подвиг и в этой сфере, став первой женщиной, избранной членом-корреспондентом Лондонского королевского общества. Знания статистики бывшая медсестра применила в здравоохранении, произведя здесь поистине революционные изменения. В своих работах она широко использовала круговые диаграммы, которые были столь наглядны, что Флоренс удалось убедить современников в своей правоте, а в результате реформы здравоохранения выиграли все мы.

В честь Флоренс Найтингейл установлен памятник на Ватерлоо-Плейс. Другой, нерукотворный памятник ей воздвигли раненые, которым она спасла жизнь.

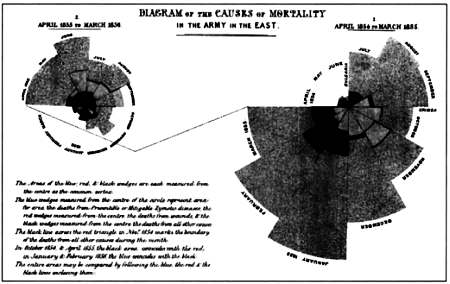
Диаграмма Флоренс Найтингейл. Вы можете видеть, как по мере реализации предложенных мер снижалась смертность.

Статистика и геноцид

Фрэнсис Гальтон (1822–1911), двоюродный брат Чарльза Дарвина, был метеорологом, астрономом, психологом, изобретателем, антропологом, исследователем и, разумеется, математиком, хотя формально так и не получил образования. Как и его двоюродный брат, он был одним из тех странствующих гениев, благодаря которым Англия достигла вершин науки. Интерес у Гальтона вызывало практически все — он занимался измерением носов, составлял карты женской красоты, изучал самовнушение и законы наследования, был превосходным статистиком и вошел в историю как автор понятий регрессии и корреляции. К несчастью, он запомнился и благодаря противоречивому понятию евгеники, которое ввел в 1865 году.

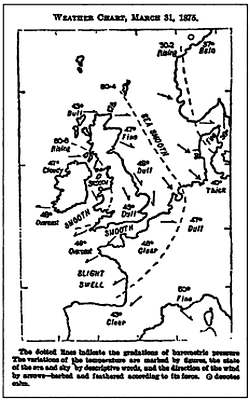
Первая в истории карта погоды, опубликованная в газете «Таймс» в 1875 году, была работой Гальтона.

Евгенику в общих чертах можно определить как улучшение населения (ранее речь в ней шла о расах) путем подавления отрицательных характеристик, препятствующих прогрессу. На протяжении нескольких десятилетий евгеника была очень модной — к ней положительно относились как правительства разных стран, так и частные лица, к примеру экономист Джон Мейнард Кейнс. Массовые эвтаназии, или плановый геноцид населения, которые стали частью евгенических программ нацистского режима, радикально изменили отношение к этому учению, и сегодня упоминать о нем считается дурным тоном.

С другой стороны, закон Харди — Вайнберга, связанный с цепями Маркова и точками равновесия, неопровержимо показывает, что устранить всех обладателей рецессивного признака в популяции гетерозиготных организмов невозможно: по мере того, как любые «аномалии», часто рецессивные и незаметные, — а также их носители — будут уничтожаться, в силу неумолимых законов наследования доля организмов, обладающих этими «аномалиями», будет возвращаться к исходной.

Евгеника стала политически некорректной, крайне сомнительной с моральной точки зрения и математически ошибочной. Но после недавнего открытия методов изменения генома человека этот вопрос вновь вышел на первый план. Закон Харди — Вайнберга по-прежнему выполняется, однако изменились сами правила игры: кажется возможным изменить ген, определяющий тот или иной рецессивный признак, и определить носителей такого гена, даже если внешне этот признак никак не проявляется. Теперь ученые могут работать напрямую с генами, а не с их носителями. Похоже, что евгеника и Гальтон вновь выходят из тени.

Теннисон и Бэббидж

Мы расскажем о двух очень разных талантливых англичанах, которые познакомились благодаря математике.

Великий поэт Альфред Теннисон (1809–1892), более известный как лорд Теннисон, считался лучшим поэтом своего времени и был избран членом Лондонского королевского общества за интерес к науке и ее распространение. Чарльз Бэббидж (1791–1871) также был членом Лондонского королевского общества, философом, инженером, криптографом и прежде всего математиком. Впоследствии Бэббидж стал одним из родоначальников вычислительной техники, автором понятия программируемой вычислительной машины, создавшим примитивное вычислительное устройство, которое он назвал аналитической машиной. Продвинуться вперед ему помешали ограниченные технические возможности того времени. Между паровыми машинами и микросхемами лежит пропасть — столь же глубокая, как и та, что разделяет приспособления эпохи Бэббиджа и современные механизмы.

Будучи членом парламента, Бэббидж отличался противоречивыми инициативами — например, он боролся с уличными шарманщиками, которых считал невыносимыми. Представьте удивление Теннисона, когда он получил от своего коллеги Бэббиджа такое письмо:

«Милостивый государь,

в вашем прекрасном стихотворении «Видение греха» (The Vision of Sin) можно прочесть строки:

Every moment dies a man

Every moment one is born

[Каждую секунду умирает человек

И каждую секунду рождается человек].

Это статистически некорректно. Если бы это в самом деле было так, число живых людей было бы неизменным. Я предлагаю вам заменить эти строки следующими или подобными им:

Каждую секунду умирает человек

Каждую секунду рождается 1 1/16

Хотя 1/16 — лишь приближенное значение вещественного числа, оно достаточно точное, чтобы его можно было привести в стихотворении.

Искренне Ваш,

Чарльз Бэббидж».

Как и следовало ожидать, предложение Бэббиджа не было услышано. Но как можно зайти столь далеко в оценке, или, точнее говоря, отрицании ценности поэзии? Представьте себе, что некто прочел строки Любовь моя, цвет зеленый. Зеленого ветра всплески и заключил, что их автору, Федерико Гарсия Лорке, следовало указать точнее, что к зеленому цвету относятся волны длиной 520–570 нанометров.

Жуликоватый булочник

В свое время титул лучшего математика мира до самой смерти носил Анри Пуанкаре (1854–1912). Рассказывают, что Джеймс Джозеф Сильвестр (1814–1897) совершил поездку в Париж с единственной целью — лично познакомиться с Пуанкаре, а встретившись с ним, не смог проронить ни слова, словно представ перед живым божеством. Пуанкаре был настолько одарен, что в студенческие годы не записал ни одного конспекта. Этот прекрасный писатель и философ, мыслитель первой величины подошел совсем близко к созданию знаменитой теории относительности. Его результаты, основанные на работах Лоренца и созвучные трудам Фитцджеральда и Минковского, были очень близки к формулировке, которую позднее разработал Эйнштейн.

Пуанкаре был выдающимся ученым, которому мы обязаны многими революционными идеями в столь далеких друг от друга областях, как теория хаоса и топология. Случай, произошедший с ним и его булочником, покажется вам странным, но достоверность этой истории подтверждается авторитетом Бостонского музея.

Анри Пуанкаре в своем кабинете.

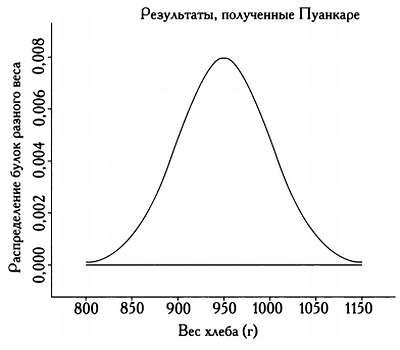
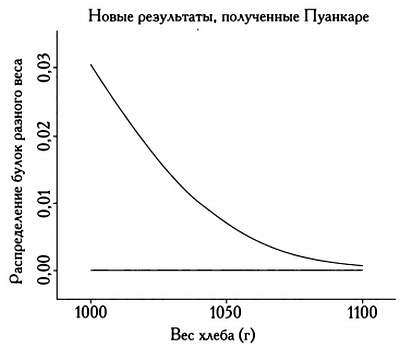
Пуанкаре обвинил булочника в том, что тот обвешивал его и продавал булки, весившие меньше положенного килограмма. Ученый стал записывать вес проданных булок и обнаружил, что он описывался кривой нормального распределения со средним значением в 950 граммов — меньше положенного килограмма. Доказательства Пуанкаре были неопровержимы, и полиция сделала булочнику предупреждение. Прошло некоторое время, и кто-то спросил Пуанкаре, перестал ли булочник обвешивать его и повысилось ли качество обслуживания в целом. Он заявил, что на оба этих вопроса нельзя ответить положительно: булочник действительно перестал его обвешивать и присылал только булки весом в 1000 граммов, но — продолжил объяснения Пуанкаре — для остальных покупателей ничего не изменилось.

И действительно, на новой кривой распределения, построенной ученым, было видно, что теперь булочник присылал ему только булки из правой части кривой, то есть весом более 1 килограмма. Кривая четко показывала, что Пуанкаре получал только булки, которые были тяжелее обычных, а булки меньшего веса, находившиеся с другой стороны кривой нормального распределения, доставались другим покупателям. Видите, как непросто обмануть статистика!

Их связали кватернионы

И сэр Уильям Роуэн Гамильтон (1805–1865), и Имон де Валера (1882–1975) были ирландцами, однако если Гамильтон был английским подданным, то де Валера стал президентом независимой Ирландии и, разумеется, обладателем ирландского паспорта. Их объединяла не только общая родина, но и любовь к математике.

Гамильтон потратил много лет на поиски алгебраического поля, которое стало бы обобщением комплексных чисел, и его поиски в конце концов увенчались успехом: в 1843 году он открыл кватернионы.

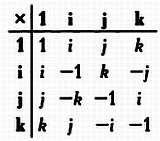
Кватернионы представляют собой сочетания символов вида

a·1 + b·i + c·j + d·k

(обычно они записываются без единицы — a + b·i + c·j + d·k, где а, Ь, с и d — вещественные числа, 1 — единица, операция умножения является дистрибутивной, а также выполняется следующее условие: х² = j² = k² = ijk = —1. Таблица умножения 1, i, j и k выглядит так:

Множество кватернионов образует поле, которое заключает в себе комплексные числа (достаточно рассмотреть кватернионы при с = d = 0). По легенде, идея о кватернионах пришла в голову Гамильтону, когда он проходил по мосту Брум Бридж в Дублине.

Это открытие показалось всем столь удивительным и столь подлинно ирландским, что много лет спустя Имон де Валера возглавил церемонию открытия памятной таблички на этом мосту. На табличке было написано:

«Здесь на прогулке, 16 октября 1843 года, сэр Уильям Роуэн Гамильтон, во вспышке гения, открыл формулу умножения кватернионов х² = j² = k² = ijk = —1, записав ее на камнях этого моста».

На этом история закончилась бы, если бы Имон де Валера (для друзей — Дев) не изучал математику и сам не был математиком. В 1913 году он предложил свою кандидатуру на должность преподавателя математики, но его не утвердили, хотя Артур Конвей, один из его преподавателей, говорил, что претендент «глубоко разбирался в теме». Когда в 1916 году де Валера находился в тюрьме, ожидая расстрела, то в ночь перед расстрелом он с гордостью написал на стене камеры вместо эпитафии:

х² = j² = k² = ijk = —1

Любить математику больше, чем он, и вправду сложно. В конце концов де Валера спасся, занялся политикой, и математика потеряла специалиста по кватернионам, однако политика от этого только выиграла. Он пережил войну (единственным опрометчивым его шагом стало выражение соболезнований Германии в связи со смертью Гитлера) и стал президентом независимой Ирландии.

Памятная табличка на мосту Брум Бридж.

Бесполезная теория

Теория множеств составляет важную часть фундамента всей математики, однако попытки преподавать ее в школах вызвали массу разногласий и споров, которые в конце концов по большей части удалось разрешить. Сегодня никто не спорит с тем, что теория множеств занимает центральное место в изучении науки, однако в начале XX века эта дисциплина, созданная благодаря усилиям Георга Кантора (1845–1918) и Рихарда Дедекинда (1831–1916), не вызвала большого интереса в академических кругах. В Принстонском университете был организован совет ученых с целью обсуждения программы преподавания математики. Предметом этой истории, которую рассказал физик и математик Фримен Дайсон (род. 1923), стал разговор между астрономом сэром Джеймсом Хопвудом Джинсом (1877–1946) и специалистом по топологии Освальдом Вебленом (1880–1960). Учебная программа казалась несколько перегруженной, и Джинс предложил облегчить ее: «Мы могли бы исключить теорию множеств — в конце концов, этот раздел математики никогда не будет особенно важным для физиков», — сказал он. Однако сэр Джеймс оказался плохим провидцем, и это подтвердят те, кто изучает квантовую механику и повсеместно использует множества.

Следуем правилам вежливости

В какой бы стране мира ни находился математик, если он увидит формулу, то сможет понять ее. Хотя научные статьи печатаются на самых разных языках (большая часть работ публикуется на английском, за ним следуют французский, русский и пиньинь), но даже в странах, находящихся за 10 тысяч километров друг от друга, используются одинаковые математические символы и сокращения. Равные величины всегда будут обозначаться знаком «=», а символ « 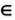» всегда означает «принадлежит к».

Когда любой человек, знакомый с математикой, видит выражения, подобные

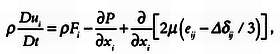
он прекрасно понимает их, даже не зная, что эта формула описывает закон сохранения импульса в жидкости.

Математическая мысль следовала многими трудными путями, пока не обрела нынешнюю форму: теперь математики всего мира могут понять друг друга, так как используют общий метаязык. Воздадим дань уважения тем, кто, часто из соображений простоты, вводил универсальные знаки, как, например,

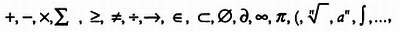
и тем, кто соглашался использовать обозначения в своих работах. До появления этих символов и сокращений математика была чрезвычайно многословной и непонятной.

Попробуйте описать привычное всем квадратное уравнение

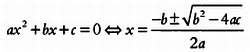
словами, не используя ни показатели степени, ни буквы, ни знаки =, + и —, ни знак деления, ни ?, ни даже логический символ <=>. Посмотрим, что у вас получится.

Авторы многих из этих знаков не слишком известны: так, например, скромный священник Уильям Отред (1574–1660) первым стал обозначать умножение знаком х, ввел сокращения sin? и cos?, а также изобрел круговую логарифмическую линейку. За всю жизнь он написал всего один труд объемом 88 страниц и в свое время считался математиком-любителем. В тот период эта наука, можно сказать, пребывала в нежном возрасте.

Когда же математика повзрослела? Один из ответов звучит так: когда было напечатано достаточно книг по математике, чтобы стало возможным определить универсальные обозначения. В 1875 году в Великобритании был учрежден комитет по унификации печатных книг, а также используемых при печати символов и сокращений. Много воды утекло с тех пор, и на свет появились совершенно новые разделы математики и математические теории, однако общие обозначения остались неизменными.

У логики есть своя логика

Американский математик и логик Уиллард Ван Орман Куайн (1908–2000) запомнился прежде всего подробными исследованиями взаимосвязей между обычным языком и языком науки. Многие ученые разделяли его точку зрения, высказанную в активной дискуссии с Жаком Деррида и другими деконструктивистами, которых Куайн считал псевдофилософами, а то и вовсе шарлатанами. Ван, как называли его друзья, много печатал на машинке, и как-то раз, направив свой ум в практическое русло, решил поменять местами несколько клавиш на клавиатуре. В частности, чтобы сэкономить время, он заменил символы «1», «!» и «?» другими, особыми логическими знаками, которые часто встречались в его записях. Как же Куайн обходился без привычных всем восклицательного и вопросительного знаков? Когда друзья спросили его об этом, то получили абсолютно логичный ответ: «Видите ли, в моем кабинете я работаю только с достоверными результатами».

Сложное домашнее задание

Американский математик Джордж Бернард Данциг (1914–2005) известен среди специалистов по линейному программированию как автор алгоритма, применяемого в решениях симплекс-методом, который играет основную роль в дисциплине под названием исследование операций. Среди любителей анекдотов он известен тем, что принял за домашнюю работу задачи, являвшиеся темой серьезных исследований.

Но эта история заслуживает более подробного рассказа.

В 1939 году одним из университетских преподавателей Данцига стал известный польско-американский математик Ежи Нейман (1894–1981), который вел курс статистики. Как-то раз Данциг опоздал на занятия и попросил Неймана не стирать написанное на доске, так как не хотел терять нить рассуждений. Он обратил внимание на два выражения, которые посчитал домашним заданием, и переписал их к себе в тетрадь. Придя домой, Данциг принялся за домашнее задание, однако оно оказалось на удивление трудоемким. Студент потратил много времени и сдал работу с опозданием. «Оставь ее в углу», — сказал Нейман, кивнув на стол, заваленный огромной кипой бумаг. Данциг молча положил свою работу сверху.

Прошло несколько недель, и однажды в воскресенье Данциг услышал звонок в дверь. Перед ним стоял взволнованный Нейман, державший в руках исписанные листы. «Быстро прочитай все, что здесь написано, — я намерен сегодня же передать это для публикации». Нейман держал в руках домашнюю работу Данцига, изложенную в виде статьи и дополненную предисловием самого Неймана. Данциг ошибочно принял за домашнее задание две важные статистические гипотезы, которые никому до этого не удавалось доказать. Он не знал об этом и доказал их, посчитав гипотезы всего лишь непростыми задачами.

Все заканчивается на «АС»

Гениального венгерско-американского ученого Джона фон Неймана (1903–1957), который, помимо прочего, считается изобретателем компьютеров, друзья называли просто Джонни. Основной принцип так называемой архитектуры фон Неймана, описывающей устройство компьютера, заключается в том, что данные и команды хранятся в общей памяти, доступной центральному процессору. В годы жизни фон Неймана появился знаменитый компьютер ENIAC (сокращение от Electronic Numerical Integrator and Computer — «электронный числовой интегратор и вычислитель») — колоссальное соединение тысяч диодов, контактов, проводов и реле, весившее почти 30 тонн и способное извлекать 33 квадратных корней в секунду с точностью до 10 знаков — немыслимая скорость в то время. После программирования и запуска ENIAC работал без вмешательства человека. Так родился предшественник компьютера HAL из фильма «Космическая одиссея 2001 года».

Джон фон Нейман, который был заядлым шутником и рассказывал забавные истории на трех языках, построил свою версию ENIAC и назвал ее Mathematical Analyzer, Numerical Integrator, And Computer («математический анализатор, числовой интегратор и вычислитель») — сокращенно MANIAC. Корпорацией RAND был создан JOHN von Neumann Numerical Integrator And Automatic Computer («числовой интегратор и автоматический вычислитель Джона фон Неймана») — сокращенно JOHNNIAC. На протяжении 13 лет, с 1933 по 1966 год, JOHNNIAC работал без передышки. В его конструкцию вносились новые и новые улучшения, и он становился все эффективнее. Эта модель намного уступала в мощности простому современному ПК, но не забывайте — на дворе стоял 1953 год!

Фотография компьютера JOHNNIAC, который в настоящее время хранится в Музее компьютерной истории в Калифорнии.

Теорема, доказанная дважды

Известный математик Пол Ричард Халмош (1916–2006) когда-то был скромным ассистентом фон Неймана — опытного исследователя и даже гения. Как Халмош рассказывал в автобиографии под названием «Хочу быть математиком» («I Want to Be a Mathematician»), в 1941 году он вместе с фон Нейманом начал работу над проектом, имевшим отношение к теории мер и теории вероятностей. Они дошли до очень серьезного этапа рассуждений, когда фон Нейман рассмотрел создание сложного вырожденного множества, при работе с которым часто приходилось прибегать к континуум-гипотезе посредством, как выражался Халмош, «неявной двойной трансфинитной индукции». Как видите, доказательство итоговой теоремы было запутанным и непростым даже для фон Неймана. Халмош пробирался сквозь математические дебри… и при этом не делал никаких заметок. Фон Нейман обратил на это внимание и предупредил помощника, но Халмош считал, что все понимает и так, поэтому не придал словам шефа особого внимания.

Настал момент записать теорему на бумаге, и тут Халмош с ужасом понял, что не может вспомнить все шаги доказательства. Что же делать? Вспомнить доказательство целиком решительно невозможно, а следующая встреча с фон Нейманом состоялась лишь спустя несколько дней.

Униженно улыбаясь, Халмош объяснил гениальному ученому, что произошло, и удостоился редкой чести наблюдать Джонни в гневе — фон Нейман никогда не выходил из себя. Ученый принялся за доказательство во второй раз, вновь преодолевая значительные трудности. К счастью, ему удалось повторить рассуждения и, потратив много времени, восстановить промежуточные действия и конечный результат, что стало настоящим подвигом даже для гения. В этот раз Халмош делал как можно более подробные записи.

Соль этого анекдота заключается в том, что Халмош стал соавтором статьи фон Неймана, озаглавленной Operator Methods in Classical Mechanics II («Операторные методы в классической механике II»). А несостоявшаяся статья под номером I стала настоящей легендой в мире физики и математики.

Сочетания с повторениями

Поэт, прозаик и — иногда — математик Раймон Кено (1903–1976), который войдет в историю как автор романа «Зази в метро» (а также текста одной из песен Жюльетт Греко), однажды вторгся в область комбинаторного анализа. До него этот же путь проделал Моцарт, однако Кено применил комбинаторику в поэзии, что на первый взгляд кажется непростой задачей. В коротенькой книжечке «Сто тысяч миллиардов стихотворений», состоящей всего из десяти страниц, на каждой из которых напечатано по одному сонету, он описал способ, позволяющий создать новые сонеты — очень современные, со множеством скрытых смыслов — на основе нескольких заранее приготовленных строчек. Для этого достаточно было взять по одной полной строчке из каждого сонета, уже напечатанного в книге. Общее число сочетаний, таким образом, равнялось 14¹⁰ — более чем достаточно даже для самого плодовитого автора. Вооружившись калькулятором, нетрудно показать, что если мы будем составлять по одному стихотворению в минуту, то для того, чтобы записать их все, потребуется немногим меньше 200 миллионов лет.

Еще один способ применения комбинаторного анализа можно увидеть в прозе Артура Кларка, который был не только писателем, но и автором серьезных научных гипотез: в частности, он предложил разместить на орбите Земли искусственные геостационарные спутники, а также первым описал космический лифт. В рассказе «Девять миллиардов имен Бога» Кларк описывает компьютер, который печатает для монахов все возможные имена Бога, составляя их с помощью обычных перестановок. Монахи верят, что когда будут записаны все имена Бога, наступит конец света. Похоже, что это действительно так: пока компьютер закончит работу над задачей, мир успеет прекратить свое существование.

Взмахи крыльев бабочки

Чтобы понять, что такое эффект бабочки, сначала нужно объяснить, что такое хаос. В 1961 году метеоролог Эдвард Нортон Лоренц (1917–2008) построил динамическую систему, которую применил в качестве модели для прогнозирования погоды. Однажды (возможно, поленившись) он ввел в компьютер число 0,506 вместо 0,506127 и, к своему удивлению, обнаружил, что это небольшое отклонение входных данных приводило к значительным изменениям состояния динамической системы. Лоренц проверял полученный результат снова и снова и всякий раз получал столь же удивительные результаты. Так официально появилась на свет одна из самых изучаемых тем в теории хаоса.

Более подробные исследования помогли несколько упорядочить этот хаос. Выходные данные по-прежнему оставались хаотическими, однако, проследовав непредсказуемыми путями, они стремились к некоему итоговому множеству, словно испытывая к нему непреодолимое влечение.

Множество всех этих бесконечно больших итоговых значений называется аттрактором. Когда точка динамической системы движется беспорядочно, хаотически, ее «пунктом назначения» на бесконечности будет точка аттрактора. Хаотическая траектория в каждый момент времени является хаотической, однако на бесконечности, в пределе, который никогда не будет достигнут, она окончит свое существование в аттракторе.

Эта точка обладает, если можно так выразиться, неотразимой притягательностью. Лоренц первым проанализировал хаос метеорологических прогнозов и описал аттрактор — множество точек, по форме отдаленно напоминающее крылья бабочки. Разумеется, это множество является фрактальным, имеет размерность Хаусдорфа, равную 2,06 ± 0,01, и представляет собой настоящее геометрическое чудо.

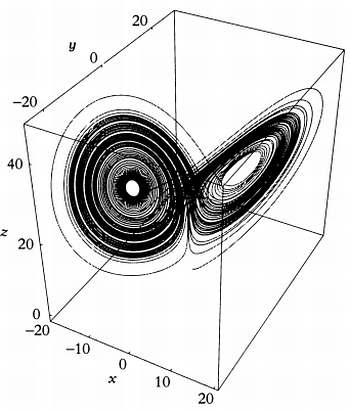
Аттрактор Лоренца — трехмерное фрактальное множество, по форме напоминающее крылья бабочки.

Тот факт, что аттрактор напоминает крылья бабочки, пробудил воображение бесчисленного множества деятелей кино и литературы. Самым известным из них был, возможно, знаменитый писатель-фантаст Рэй Бредбери: в своем рассказе «И грянул гром» он описывает путешествие во времени, в ходе которого гибель одной доисторической бабочки приводит к значительным изменениям в современной политике — вместо либерального президента народ избирает ужасного диктатора-фашиста. Сложно найти более привлекательный образ: простой взмах крыльев бабочки в далеком прошлом способен определить настоящее, которое, как кажется, не имеет к этой бабочке никакого отношения. Динамические системы могут быть хаотическими, а небольшие предпосылки могут иметь огромные последствия. На небольших промежутках времени — ничто по сравнению с вечностью — предопределения не существует; хаос нависает грозной, бесконечно грозной тенью, которая не позволяет делать какие-либо прогнозы. На длительных промежутках времени наблюдается аттрактор, существующий необъяснимо далеко, в пределе, на границе бесконечности.

Лучшее — враг хорошего

Для чистокровного демократа из тех, что голосуют по любому поводу и верят, что их голос поможет изменить положение в обществе, идеалом является совершенная система голосования, удовлетворяющая определенным требованиям. Известны множество систем голосования (например, в Испании применяется метод д’Ондта), однако должна же существовать некая суперсистема, которая будет лучшей среди них. Ее предполагаемые характеристики, снабженные обширными комментариями, можно найти в интернете. Так как подробные описания различных систем голосования слишком объемны и скучны, не будем приводить их полностью. Ограничимся следующим указанием: идеальная система голосования, позволяющая принять общее решение на основе предпочтений отдельных лиц, должна соответствовать пяти разумным требованиям.

1. Отсутствие диктатуры: никакие личные предпочтения одного человека не могут влиять на остальных.

2. Индивидуальное упорядочение: каждый должен уметь упорядочивать свои предпочтения.

3. Единодушие: если все выбирают какой-то вариант, он является окончательным.

4. Единственность: результат голосования всегда будет одним и тем же, если предпочтения избирателей не меняются.

5. Независимость незначащих альтернатив: если исключить из голосования один вариант, остальные не изменятся.

Лауреат Нобелевской премии по экономике 1972 года Кеннет Эрроу (род. 1921) подробно изучил вышесказанные характеристики с точки зрения математики и вынес удивительный вердикт: не существует системы голосования, которая соответствовала бы всем указанным условиям. Она может соответствовать некоторым

из них, но не всем одновременно. «У каждого свои недостатки», как говорил герой

Билли Уайлдера в фильме «В джазе только девушки».

Красноречивое название

Американский математик Ив Нивергельт был автором работ о компьютерах, вейвлетах и статистике. Одна из его статей, опубликованная в 1987 году, стала настоящим бестселлером среди студентов, изучающих экономику и социологию. В ней, в частности, идет речь о математическом понятии эластичности.

Непосвященный напрасно будет пытаться понять, в чем же заключено очарование этой статьи: она полна формул с производными, логарифмами и другими математическими ужасами. Если вы прочитаете статью до конца, то узнаете, что курить — вредно, а антитабачные пошлины почти не влияют на курильщиков, однако позволяют выручить средства, которые затем направляются на борьбу с курением.

Также в статье рассказывается, что спрос на лосося, помимо прочих факторов, зависит от его относительной численности, от выживаемости икринок и молодых особей и так далее. Словом, вы узнаете много интересного о самых разных явлениях.

Не просто игра

Если какую-то игру и можно назвать царицей игр, то этого титула, несомненно, заслуживают шахматы. В них случайность никак не влияет на ход игры, а определяющее значение имеют чистая стратегия и память: число возможных ходов в партии имеет порядок 10¹²³ — это невообразимая величина. Однажды чемпионом мира по шахматам стал профессиональный математик Эмануэль Ласкер (1868–1941).

Сейчас мы говорим о стандартных шахматах на доске из 64 клеток, но еще в далекую викторианскую эпоху математик Артур Кэли (1821–1895) уже рассмотрел трехмерные шахматы, в которые сегодня играют персонажи сериала «Звездный путь».

Пока что никто не смог должным образом изучить эту игру — она слишком сложна даже для передовых методов современной теории игр. Но существует несколько ценных результатов: испанский инженер Леонардо Торрес Кеведо (1852–1936) в 1914 году сконструировал шахматный автомат, который всегда одерживал победу в окончании шахматной партии для трех фигур (король против короля и ладьи). Конечно, мы по-прежнему далеки от заветной цели — алгоритма, указывающего путь к победе в любой партии, но надо же с чего-то начать.

Машина под названием «Турок», сконструированная венгерским инженером Вольфгангом фон Кемпеленом в 1769 году, произвела фурор. Казалось, что машина способна играть в шахматы, однако на самом деле она была искусной фальшивкой — внутри механизма прятался человек.

Шахматы — прекрасное поле битвы, можно даже сказать, первой битвы в вечном противостоянии человека и машины. Известно, что шахматные программы становятся все совершеннее, и сложно устоять перед соблазном столкнуть лицом к лицу гроссмейстера и такую программу. В 1996 году уже состоялся поединок между компьютером Deep Blue, созданным компанией IBM, и чемпионом мира по шахматам Гарри Каспаровым. Каспаров выиграл со счетом 3:0. Таким образом, в 1996 году человек опередил машину.

На следующий год программное обеспечение Deep Blue было улучшено, и поединок прошел вновь. Теперь машина одержала верх. Каспаров остался не слишком доволен результатом и предположил, что во время партии в действия компьютера вмешивался человек. Компания IBM, как и следовало ожидать, отвергла обвинения. Желаемая цель, отчасти пропагандистская, была достигнута, и после этого компьютер был разобран. В 2000 и 2003 годах прошли новые поединки между гроссмейстерами и компьютерами, сменившими Deep Blue, все они завершились ничьими. Вероятно, в будущем мы увидим новые партии между человеком и машиной.

В конце концов люди запомнят только одно: благодаря техническому прогрессу машина одержала верх над человеком — рано или поздно это все равно произойдет. Однако по-настоящему важен ответ на другой вопрос: подобно ли мышление человека мышлению машины? Этого мы пока не знаем. Быть может, мы не узнаем этого вообще никогда, и вопрос останется гёделевским утверждением, дать ответ на которое невозможно.