Приложение Фигурные числа

Приложение

Фигурные числа

Фигурное число — это число, которое может быть представлено в виде точек, расположенных в форме правильного многоугольника. Эти числа долгое время служили объектом пристального внимания математиков. Греки приписывали им магические свойства, связанные с их особой формой, а Диофант посвятил им отдельный труд.

Треугольное число можно представить в виде равностороннего треугольника:

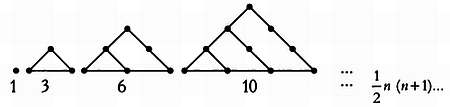
Получим последовательность 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91,105…

Общая формула приведена справа от иллюстрации.

Квадратные числа можно представить в форме квадратов:

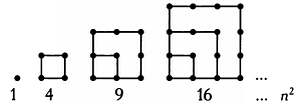
Получим последовательность 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225… Общая формула — n².

Пятиугольные числа можно представить в виде пятиугольников:

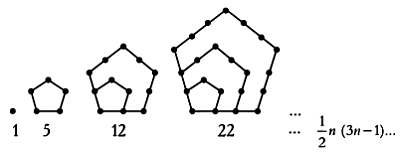
Получим последовательность 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330… Общая формула приведена на рисунке.

Аналогично можно получить шестиугольные, семиугольные числа и так далее.

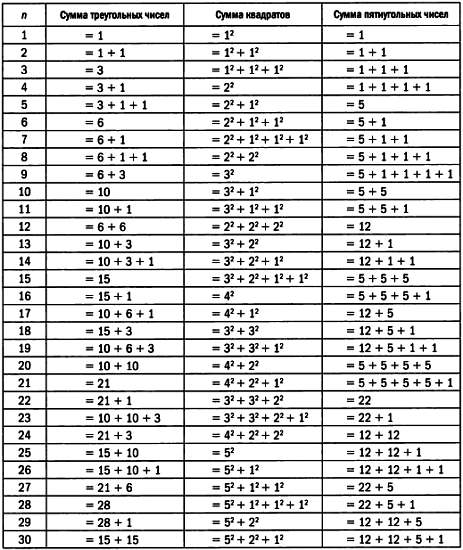
Ферма первым понял, что любое натуральное число можно представить как сумму максимум трех треугольных, четырех квадратных, пяти пятиугольных чисел и так далее. Данные, представленные в следующей таблице, позволяют убедиться, что это соотношение выполняется для треугольных и пятиугольных чисел.