Лодка и бутылка

— Твое решение задачи о лодке звучит прямо как специальная теория относительности Эйнштейна, — заметил один из яхтсменов.

— Речь идет всего лишь об относительном движении. В этом ты прав, но до специальной теории относительности очень далеко, — возразил другой яхтсмен, большой любитель научно-популярной литературы. — Но этот случай напомнил мне другую историю, в которой важную роль играет, какую систему координат выбрать для описания явлений.

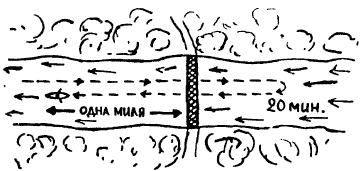
Однажды некто греб в лодке по реке против течения. На носу лодки стояла наполовину уже пустая бутылка отличного виски. Когда гребец проплывал под мостом, лодку слегка качнуло, и бутылка упала за борт. Не заметив пропажи, человек в лодке продолжал грести против течения, а бутылка между тем поплыла по течению. Через 20 минут человек заметил, что бутылка исчезла, повернул назад (временем, необходимым для совершения поворота, можно пренебречь) и поплыл вдогонку за бутылкой. Будучи от природы флегматичным, он продолжал грести в том же темпе, в каком греб против течения, но если его скорость относительно берегов до поворота была равна разности между скоростью лодки и скоростью течения, то теперь она стала равна сумме тех же скоростей. По прошествии некоторого времени гребец увидел бутылку и подобрал ее в одной миле[12] от моста (ниже его по течению).

Может ли кто-нибудь на основе этих данных сказать, какой была скорость течения?

Несколько членов клуба, любители математики, принялись решать задачу, а один из них даже составил алгебраическое уравнение, связывавшее две неизвестные величины: скорость лодки относительно воды и скорость течения реки. Но ни прямой, ни алгебраический подход не позволили решить задачу, и в конце концов знатоки пришли к заключению, что данных просто недостаточно.

— И все же решение задачи существует, причем очень простое, — заявил яхтсмен, предложивший задачу. — Необходимо лишь рассматривать задачу в системе координат, движущейся вместе с водой в реке. В такой системе координат вода в реке как бы останавливается (река превращается в озеро), а берега и мост движутся относительно системы координат. Если вы плывете на гребной лодке по озеру, уронили что-нибудь в воду и подобрали пропажу через 20 минут после того, как заметили ее, то вам понадобится ровно 20 минут, чтобы вернуться в то место, откуда вы устремились вслед за пропажей. Таким образом, бутылка пробыла в воде 40 минут, а за это время мост переместился относительно воды на 1 милю. Следовательно, скорость моста относительно воды или, что то же самое, скорость течения относительно моста и берегов составляет 1 милю за 40 минут, или 1,5 мили в час. Просто, не правда ли?

— Но вы не можете таким же способом найти скорость лодки, — заметил яхтсмен, пытавшийся решить задачу с помощью алгебраического уравнения. — Ведь в задаче две неизвестные величины.

— Вы правы, но скорость лодки относительно воды не имеет отношения к задаче, и я не просил найти ее. Трудность, с который вы столкнулись, пытаясь решить задачу алгебраически, связана с тем, что вы пытались найти две неизвестные величины, располагая лишь одним уравнением. В действительности вторая неизвестная величина выпадает, но уравнение выглядело таким сложным, что вы этого не заметили.