Глава 7. От деления по уровню успеваемости к делению с ориентацией на мышление роста

Возможности для обучения

Я до сих пор хорошо помню свой первый урок математики в качестве учителя. Это было в школе Хаверсток в лондонском районе Кэмден-Таун (о ней шла речь в главе 6). Когда я начала там работать, в преподавании математики использовалась система деления учеников на группы по уровню успеваемости. Дети учились вместе до девятого класса, а потом их зачисляли в одну из четырех групп. В тот день я пришла на свой первый урок, воодушевленная возможностью объяснять математику девятиклассникам, вооружившись научными знаниями об эффективном преподавании. Но моих учеников только что зачислили в группу самого низкого уровня. Я поприветствовала их, а они мне сказали: «А смысл?» Я целый год старалась подавать им вдохновляющие сигналы и использовала методы, которым научилась во время профессиональной подготовки, но их путь был предопределен заранее и я мало что могла изменить. Я добилась отмены деления учеников на группы по уровню успеваемости; с тех пор эта школа дает всем ученикам возможность изучать математику высшего уровня.

Один из главных факторов успеваемости учеников — «возможности обучения». Если у детей есть доступ к сложному материалу, они добиваются лучших результатов. Это неудивительно, удивляет другое: все мы знаем, что возможность учиться — самое важное условие (Wang, 1998; Elmore & Fuhrman, 1995), но миллионы учеников лишены возможности осваивать материал, который им нужен и который они потянули бы, поскольку их зачисляют в классы более низкого уровня, порой с самого раннего возраста. Я была потрясена полученными в Англии статистическими данными: 88% учеников, которых распределили по группам в возрасте четырех лет, остались там же на протяжении всего периода учебы в школе (Dixon, 2002). Тот факт, что будущее детей определяют за них, когда им всего четыре года или даже четырнадцать лет, губительно сказывается на работе учителей и школ и противоречит результатам фундаментальных исследований по теме развития и обучения. Дети развиваются разными темпами и в разное время; на разных этапах у них проявляются разные интересы, сильные стороны и склонности. Мы не можем знать, какими способностями будет обладать ребенок в четыре года или четырнадцать лет, поэтому стоит создать среду, в которой они могут осваивать материал высокого уровня и которая будет подпитывать их интересы, а учителя готовы в любой момент распознать, взрастить и развить их потенциал. Новые научные данные о невероятной способности головного мозга расти и меняться, наряду с данными о важности представлений учеников о собственном потенциале, подтверждают необходимость выхода за рамки устаревших систем деления на группы по уровню знаний (сформировавшихся в те времена, когда у нас было меньше информации), которые ограничивают достижения учеников, каким бы ни был их уровень успеваемости раньше.

Однажды я выступала перед более чем 800 учителями математики и руководителями школ и задала им такой вопрос: «Какие методы, которые используются в школах в настоящее время, способствуют формированию фиксированного мышления?» Все записали свои ответы на листах бумаги, и я их собрала. В записках часто упоминались методы обучения, о которых идет речь в данной книге (особенно оценка уровня знаний и система оценок, подробнее см. главу 8), но был и явный лидер: деление на группы по способностям. Я согласна с этим. Нет более сильного сигнала о фиксированном мышлении, чем навешивание ярлыков. Такой сильный сигнал негативно сказывается на всех учениках, в какую бы группу они ни попали (Boaler, 1997; Boaler, 2013a; Boaler & Wiliam, 2001; Boaler, Wiliam, & Brown, 2001). Карисса Ромеро (докторант, которая работала вместе с Кэрол Дуэк, а затем стала руководителем одного из отделений Стэнфордского университета) пришла к выводу, что сигналы о фиксированном мышлении, которые получают ученики при делении на группы по уровню успеваемости, наиболее негативно сказываются на детях, которые попадают в группы высшего уровня (Romero, 2013).

Отказ от деления учеников на группы по уровню успеваемости

Во многих школах США учеников зачисляют в группы по изучению математики, сформированные по принципу успеваемости, начиная с седьмого класса. Создаются отдельные классы, в которых подросткам преподают материал соответствующего уровня. Международные аналитики, изучающие уровень знаний по математике в разных странах, пришли к важному выводу: самых больших успехов добились те страны, в которых меньше всего делят учеников на группы по способностям. Например, в ходе третьего международного исследования по математике и естественно-научным дисциплинам было обнаружено, что в США имеет место самый высокий разброс успеваемости учеников — иными словами, самый высокий уровень разделения на группы по способностям. Страной с самым высоким уровнем успеваемости стала Южная Корея; там реже использовалось деление на группы и успеваемость распределялась наиболее равномерно. В США была также обнаружена самая сильная корреляция между уровнем успеваемости и социально-экономическим статусом. Этот результат был отнесен на счет деления учеников на группы (Beaton & O’Dwyer, 2002). Самый высокий в мире уровень знаний по математике отмечен в таких разных странах, как Финляндия и Китай, причем в обеих отказываются от деления на группы по способностям и преподают сложные дисциплины всем. В объединенном школьном округе Сан-Франциско, одном из крупнейших школьных округов Калифорнии, было решено отказаться от всех форм деления на группы и отменить углубленные курсы до десятого класса. Вплоть до перехода в десятый класс учеников стимулируют изучать математику на как можно более высоком уровне. До этого момента все могут осваивать анализ, а в дальнейшем у всех детей есть доступ ко всем углубленным курсам. Это исключительный случай, и он заслуживает восхищения. Внимательно изучив результаты научных исследований, школьный совет единогласно утвердил предложение об отмене устаревших форм деления на группы. В большинстве школьных округов учеников распределяют по группам в гораздо более раннем возрасте. В округе, расположенном в весьма успешном районе неподалеку от Стэнфорда, половину детей зачисляют в группы низкого уровня, когда они переходят в седьмой класс, лишая их возможности в дальнейшем изучать анализ. Именно в этот момент родители должны услышать тягостный звук: хлопок двери в будущее для их детей. Если мы хотим начать новую эпоху, в которой все стремятся изучать математику высокого уровня, необходимо перейти к более гибким методам деления на группы, основанным на результатах научных исследований (о них пойдет речь ниже).

Учителям трудно давать всем ученикам задания, соответствующие уровню каждого, но они знают золотую середину, позволяющую добиться поразительной вовлеченности всего класса: когда задания достаточно сложны для детей, но не выходят за рамки их возможностей. На первый взгляд кажется, что сделать это легче, если разделить учеников на группы по уровню успеваемости. Но в этом случае ученики показывают более низкие результаты, поскольку даже в таких группах у детей разные интересы и разная подготовка. Однако учителя продолжают считать всех учеников одинаковыми и выбирают узкие задания, состоящие из коротких вопросов — слишком легкие для одних и слишком трудные для других. Именно поэтому постановка задач категории «низкий пол, высокий потолок» на уроках математики так важна для будущего. Другая, более очевидная причина того, что деление учеников на группы снижает успеваемость, — сигнал о фиксированном мышлении, который оно подает всем ученикам.

Исследования показывают, что происходит, когда школы решают отказаться от деления на группы по уровню успеваемости. Одна важная работа продемонстрировала последствия отказа от такого деления в школьном округе Нью-Йорка. В прошлом ученики средних школ Нью-Йорка занимались в обычных классах и классах с углубленным изучением математики. Затем в округе приняли решение отменить специализированные классы и преподавать всем математику высшего уровня сложности. Исследователям удалось отслеживать успеваемость учеников на протяжении трех лет занятий в классах, сформированных по принципу успеваемости, а затем трех лет обучения в смешанных классах. Они изучали учеников шести возрастных групп вплоть до окончания старшей школы. Было установлено, что те, кто изучал математику более высокого уровня в общих классах, получали больше удовольствия от нее и сдали тест штата Нью-Йорк на год раньше, чем ученики, которые были поделены на группы по принципу успеваемости. Вдобавок оказалось, что отказ от такого деления полезен ученикам с разными уровнями успеваемости (Burris, Heubert, & Levin, 2006). Эти выводы подтверждают многие другие исследования (см., например, Boaler, 2013b). Результаты многих работ указывают на негативное влияние деления на группы по уровню успеваемости, но эта практика до сих пор существует в большинстве школ США. Ниже я расскажу, как во время занятий можно использовать современные и эффективные методы деления учеников на группы, обеспечивающие всем возможность учиться и развивать мышление роста.

Деление на группы с ориентацией на мышление роста

Джилл Баршей — журналист Hechinger Post. Ее популярная колонка «Образование в цифрах» публикуется раз в неделю в U.S. News & World Report. После того как Джилл прочла мою книгу «При чем тут математика?» и прошла онлайн-курс для учителей, у нее появилось желание преподавать математику. Она стала учителем алгебры в девятом классе чартерной школы в Бруклине. Но она не знала, с какими учениками ей предстоит столкнуться: деморализованными, которые, по сути, поставили крест и на математике, и на себе, поскольку их не зачислили на курс алгебры в восьмом классе. Дети заявили Джилл, что они не «умники», и весь год вели себя очень плохо. К сожалению, это одно из следствий деления учеников на группы по успеваемости. В большинстве своем плохо ведут себя ученики, которые не верят, что могут добиться успеха. Учителя беспокоятся, что в общих группах ученики с плохим поведением будут оказывать негативное влияние на остальных. Однако дети ведут себя плохо только тогда, когда им внушают мысль, что они не смогут ничего добиться. Как можно их за это винить? За все годы преподавания в разношерстных группах учеников я пришла к выводу, что, когда дети начинают верить в себя и понимают, что я верю в них, плохое поведение и отсутствие мотивации сходят на нет.

Я много лет работала в замечательной средней школе, которая демонстрирует твердую приверженность преподаванию, ориентированному на мышление роста, и в которой всегда разделяли учеников на группы по смешанному принципу. Несколько лет назад в ней начали ощущать давление со стороны родителей, которые требовали математических классов, чтобы их дети могли перейти в старшую школу, заранее изучив геометрию. В итоге школа сдалась, и в ней появились обычные классы и классы с углубленным изучением математики. Это изменение оказалось катастрофичным: множество учеников разных уровней потеряли интерес к математике. У учеников с одинаковым уровнем успеваемости, зачисленных в разные группы, возникли серьезные проблемы, у многих сформировалась установка на данность в отношении своих способностей. Кроме того, многие ученики, которые попали в классы с углубленным изучением математики, стали испытывать неприязнь к этому предмету и предпочли уйти оттуда, что нанесло им еще больший вред. Через два года школа отказалась от деления учеников по успеваемости и вернулась к смешанным группам. Сейчас она предлагает всем желающим курс геометрии в качестве факультатива, проводимого до начала уроков. Эта превосходная стратегия позволяет справиться с давлением родителей, предоставляя возможность выбора тем, кто хочет пройти углубленный курс математики, но не подавая ученикам губительных сигналов об их потенциале, формирующих фиксированное мышление.

Учителя, которые хотят дать всем ученикам возможность освоить материал высшего уровня, но вынуждены проводить уроки в классах, сформированных по принципу успеваемости, порой дают сложные задания. Им хорошо известно, что деление по уровню успеваемости ограничивает достижения учеников. Кроме того, они знают, что при наличии правильных сигналов и грамотного преподавания ученики классов низшего уровня способны выполнять более сложные задания.

В еще одной замечательной городской школе, где придерживаются подхода, ориентированного на мышление роста, учителя отказались от формирования классов по принципу успеваемости и ввели дополнительные занятия для слабых учеников. Их могут посещать все дети, которым необходимо чуть больше времени для изучения материала. Дополнительные занятия проводятся после обычных уроков математики, включенных в расписание, и не посвящены работе над ошибками. Ученики могут вернуться к материалу занятий обычной школьной программы и обсудить его, более тщательно проанализировав математические концепции, которые рассматривались на уроке. Приходят и те, кому математика дается с трудом, и те, что справляются с ней, но стремятся глубже изучать этот предмет. Название курса не подразумевает, что он предназначен только для учеников с низкой успеваемостью.

Учителя, которые стремятся создать новое будущее (где всем свойственно мышление роста и у всех есть благоприятные возможности) и предпочитают работать в смешанных классах, достойны восхищения. Но обучение групп с широким диапазоном успеваемости требует компетентного подхода. В таких группах не получится объяснять узкие математические темы, которые смогут понять немногие. Ниже я расскажу о ряде важных стратегий эффективного преподавания в разнородных группах, которые опираются на результаты научных исследований.

Эффективное преподавание в смешанных группах: задачи по математике

При отказе от разделения на группы по уровню успеваемости на уроках математики очень важно обеспечить возможность изучать математику на разных уровнях, а также не ставить закрытые вопросы, подходящие для немногих. Есть разные способы стимулировать изучение математики на разных уровнях.

1. Постановка открытых задач

Как было сказано в главе 5, если ученикам, входящим в состав разнородной группы, ставить закрытые вопросы, многие из них не смогут дать ответ или проявить себя. Поэтому крайне важно ставить открытые задачи из категории «низкий пол, высокий потолок». Они позволяют всем усвоить соответствующие математические концепции и поднять их понимание на очень высокий уровень. К счастью, задачи категории «низкий пол, высокий потолок» относятся также к числу самых увлекательных, имеющих большую ценность и помимо того, что они рассчитаны на детей с разными уровнями успеваемости. Они знакомят учеников с важными математическими концепциями, которые пробуждают у них интерес и стимулируют творческий подход. В главе 5 приведен ряд примеров таких задач, а также ссылки на сайты, на которых можно найти их описание.

Учителя успешной английской школы Феникс-Парк, использующей проектно-ориентированный подход, подобрали ряд задач категории «низкий пол, высокий потолок», которые могли решать все дети. Некоторые решали их успешно в одни дни, а другие — в другие дни. Было невозможно предвидеть, какие ученики будут решать задачи на каком уровне в конкретный день. В главе 5 приведен пример задачи о максимальной площади, которую можно огородить забором; благодаря ей одни ученики узнали о тригонометрии, другие — о теореме Пифагора, а третьи — о фигурах и площади. Роль учителя во время уроков сводилась к обсуждению заданий, над которыми работали ученики, а также к тому, чтобы направлять детей и расширять их мышление. Во время обычного урока эту роль выполняет учебник, темы и задачи по математике, которые в нем представлены. Но это грубый инструмент, который не способен определить, что знает ученик или что ему нужно знать. Во время уроков, ориентированных на мышление роста, именно учитель принимает решения, которые касаются отдельных детей или групп и направлены на то, чтобы дать ученикам возможность проявить себя, поддержать их и помочь им выйти за привычные рамки на своем уровне. При работе над открытыми задачами учителя могут взаимодействовать с учениками, знакомить их с математическими концепциями и обсуждать важные вопросы. Потому-то в такой среде ученики добиваются больших успехов. Этот подход требует от учителей серьезного напряжения, но приносит им огромное удовлетворение, особенно когда они видят, как дети, которым раньше не хватало уверенности в себе и у которых была низкая успеваемость, взлетают и стремительно набирают высоту.

Несколько лет назад в Англии я работала с группой учителей, которые решили отказаться от деления на группы по уровню успеваемости в старших классах, когда узнали о методе комплексного обучения, описание которого приведено ниже. У них не было ни специальной подготовки, ни такой замечательной программы, как в школе Феникс-Парк, но они узнали о комплексном обучении и подобрали ряд задач категории «низкий пол, высокий потолок». В конце первой недели преподавания в новых классах, сформированных с ориентацией на мышление роста, один учитель с удивлением обнаружил, что первым задачу решил ученик, который раньше был в группе самого низкого уровня. И позже этих учителей приятно удивляло то, что ученики с разными уровнями успеваемости используют творческие методы решения задач. Они были в восторге от того, насколько хорошо ученики отреагировали на отказ от деления на группы по успеваемости. Вдобавок и проблемы с дисциплиной, обострения которых они опасались, исчезли. Мне было интересно узнать об этом, поскольку эти учителя выражали обеспокоенность по поводу отказа от формирования групп по успеваемости и по поводу того, смогут ли дети работать вместе. Учителя обнаружили, что, когда они дают открытые задачи, все ученики проявляют к ним интерес, стараются проявить себя и получают необходимую поддержку. Со временем ученики, которых раньше считали слабыми, повысили свой уровень. При этом класс не делился на «способных» и «неспособных». Он состоял из увлеченных детей, которые учатся вместе и помогают друг другу.

2. Предоставление возможности выбирать задачи

Ученикам, которые занимаются в классах, ориентированных на мышление роста, не всегда нужно работать над одними и теми же задачами. Им можно предложить разные задания разных уровней и из разных областей. Важно, чтобы сами ученики могли выбирать задачу, над которой хотят работать, а не учителя. Однажды во время урока в школе Феникс-Парк, на котором я присутствовала, ученикам предложили выбрать одну из двух задач: найти фигуры, площадь которых составляет 64 единицы; найти фигуры, объем которых составляет 216 единиц. В четвертом классе я видела, как учитель предлагает ученикам использовать дробные полоски или палочки Кюизенера, для того чтобы найти как можно больше дробей, эквивалентных ¹/₄, а в качестве дополнительного, более трудного задания — найти дроби, эквивалентные ²/₃. Расширенные задания и различные задачи с дополнительными вопросами — это и есть то, что можно (и, пожалуй, целесообразно) делать на каждом уроке. Все ученики должны иметь возможность выбора или решения более сложных и интересных задач.

Порой некоторых учеников необходимо подталкивать к тому, чтобы они взялись за решение предложенной на уроке задачи повышенной сложности. При постановке задач важно, чтобы у учеников не возникала мысль, будто они могут работать только над простой задачей или учитель не считает их способными решить что-то более сложное. Наблюдая, как эту стратегию применяют разные учителя, я видела, как они сообщают ученикам информацию о том, что задачи охватывают разные темы или некоторые из них особенно сложны. Ученики счастливы, когда у них есть возможность решать, над чем они хотят работать и когда им предлагают дополнительные, более сложные и интересные задачи.

3. Индивидуальные пути обучения

В период преподавания в смешанных группах школы Хаверсток я использовала курс математики, который специально разработан для групп с разной успеваемостью, сформированных в городских школах. Он получил название SMILE, или Secondary Mathematics Individualized Learning Experience («Практика индивидуального обучения математике в средней школе»)[17]. Лондон — удивительный город, который отличается большим разнообразием и высоким уровнем текучести учеников. Учителя, которые работают в школах Центрального Лондона, знают, что у них в один день может быть одна группа учеников, а на следующий день состав группы может измениться, поскольку некоторые ученики уходят из класса, а другие присоединяются к нему. Многие учителя из центральных районов Лондона придерживались принципа формирования разнородных групп, в состав которых входят дети с разными уровнями успеваемости. В отличие от традиционных учебных программ, курс SMILE представлял собой комплект карточек (листов бумаги стандартного размера), которые составляли учителя, пытаясь сделать их как можно более увлекательными и учитывающими культурные особенности. Курс включает тысячи карточек, каждая из которых посвящена отдельной теме. Любой учитель из центральных районов Лондона мог предложить свою карточку; со временем комплект разросся до трех тысяч интересных карточек, составленных учителями. Учителя, преподававшие курс SMILE, выдавали каждому ребенку 10 карточек, которые тот должен был проработать и показать преподавателю, после чего получал еще 10 карточек. Карточки предоставлялись каждому ученику в отдельности, но на многих предлагалось найти партнера для совместной работы над соответствующими математическими концепциями.

Поскольку карточки подбирались индивидуально, ученики могли работать с ними в удобном темпе, а учителя ходили по классу и помогали им. Я сама преподавала курс SMILE и видела очень увлеченных детей, которые с воодушевлением собирали карточки, зная, что их успех зависит от них самих. Иногда мы не работали с карточками, а всем классом проводили математические исследования. Курс SMILE был весьма эффективен в городских школах со смешанными классами, поскольку предусматривал возможность индивидуальной работы, а отсутствие кого-то из учеников не создавало проблем в классе. Многие карточки SMILE превосходны, но порой их необходимо адаптировать к местным условиям, поскольку они рассчитаны на лондонских учеников и содержат много примеров, касающихся Лондона.

Развитие технологий привело к тому, что индивидуальный подход к обучению математике получил более широкое распространение. Основатель Khan Academy Сал Хан — знаменитый приверженец индивидуального обучения. Он справедливо подчеркивает примитивность деления на группы по успеваемости и показывает, как ученики, которым дается возможность самим выбирать материал и путь обучения, добиваются гораздо больших успехов, независимо от начального уровня (Khan, 2012). Другие компании, работающие на основе современных технологий, также создали продукты, позволяющие ученикам заниматься на своем уровне. Однако, как ни печально, я еще не встречала такой продукт для индивидуальной работы, который обеспечит эффективное обучение математике. Но сам принцип предоставления ученикам возможности формировать свой путь обучения и получать индивидуальный материал в сочетании с условиями для групповой работы и сотрудничества позволяет предлагать задания высокого уровня всем ученикам.

Эффективное преподавание в смешанных группах: комплексное обучение

Задачи по математике, которые используются в смешанных группах, очень важны. Но не менее важны и правила, и ожидания в отношении того, как ученики должны работать вместе. Опытные учителя знают, что групповая работа на уроках может закончиться неудачей, если ученики принимают в ней неравноценное участие. Если дети предоставлены себе и их никто не стимулирует к формированию эффективных правил работы в группе, скорее всего, произойдет вот что: некоторые возьмут на себя большую часть работы, другие будут сидеть сложа руки, а кого-то вообще могут не допустить к работе, потому что они не имеют авторитета в глазах других. Социолог Стэнфордского университета Элизабет Коэн проанализировала закономерности неравного участия в групповой работе во время уроков и пришла к выводу, что это связано с социальными различиями между членами группы: некоторым ученикам присваивают или они сами принимают статус важных участников группы, а на других навешивают ярлык низкого статуса (Cohen, 1994). Моя коллега из Стэнфорда Дженнифер Лэнгер-Осуна изучила много примеров групповой работы, в которых основанием для рассмотрения идей был воспринимаемый статус ученика, который их выдвигает, а не математическое содержание (Engle, Langer-Osuna, & McKinney de Royston, 2014). Она пришла к выводу, что различия в статусе часто обусловлены стереотипными установками в отношении учеников определенной расы, социального положения или пола (Esmonde & Langer-Osuna, 2013; Langer-Osuna, 2011). Лиз Коэн и Рейчел Лотан разработали комплексный педагогический подход, направленный на обеспечение равенства в процессе групповой работы. Его можно использовать в любом классе и в преподавании любого школьного предмета (Cohen & Lotan, 2014).

В ходе четырехлетнего научного исследования, которое финансировал Национальный научный фонд, я сравнила разные подходы к преподаванию математики. Вместе с командой своих студентов я отслеживала успехи более 700 учеников разных старших школ (Boaler, 2008; Boaler & Staples, 2005). Примерно половину участников составляли ученики школ, в которых классы формировались по принципу успеваемости, преподавание математики носило формальный характер, а уровень знаний оценивался с помощью тестов. Другая половина участников — ученики городской школы в Калифорнии, которую я назвала Рейлсайд. В ней учителя отказались от деления учеников на группы по уровню успеваемости и преподавали математику в рамках комплексного подхода. Состав учеников этой школы был очень разнородным; в ней было больше учеников, изучающих английский язык, и более высокий уровень культурного многообразия, чем в любой другой школе. В Рейлсайд было примерно 38% учеников-латиноамериканцев, 23% афроамериканцев, 20% белых, 16% учеников азиатского происхождения и выходцев с тихоокеанских островов, 3% представителей других групп. В начале нашего исследования, когда ученики только окончили среднюю школу, мы организовали оценку уровня знаний по математике за прошедший период. В то время успеваемость учеников Рейлсайд была гораздо ниже по сравнению с другими городскими школами, принимавшими участие в исследовании, что не так уж нетипично для городской среды, в которой ученикам приходится решать много жизненных проблем (рис. 7.1).

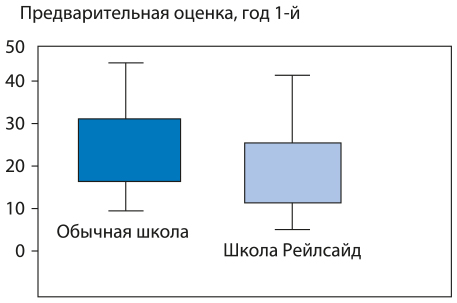
Рис. 7.1. Результаты предварительной оценки уровня знаний

Через год ученики Рейлсайд догнали тех, которые учились традиционным способом (рис. 7.2). Через два года их уровень успеваемости стал гораздо выше (рис. 7.3).

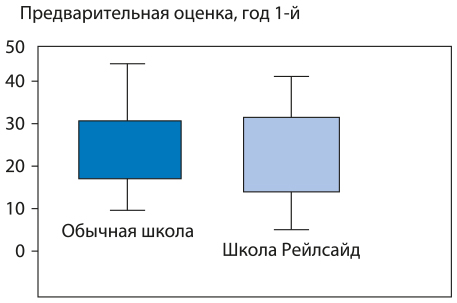
Рис. 7.2. Результаты оценки уровня знаний, год 1-й

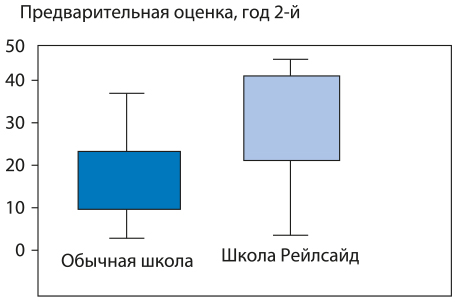
Рис. 7.3. Результаты оценки уровня знаний, год 2-й

Кроме того, ученики Рейлсайд получали гораздо большее удовольствие от математики и продолжили изучать этот предмет на более высоком уровне. В школе 41% учеников прошли углубленный курс начал анализа и анализа (из тех, кто обучался традиционным способом, таких было 27%). Кроме того, в Рейлсайд снизилось или исчезло расовое неравенство в плане успеваемости учеников (YouCubed at Stanford University, 2015a).

Не так давно была опубликована важная книга, посвященная анализу достижений Рейлсайд и применяемых в ней справедливых методов обучения, которую написали учителя этой школы (Nasir, Cabana, Shreve, Woodbury, & Louie, 2014).

Ниже представлен анализ того, как школе удалось добиться таких впечатляющих результатов, придерживаясь четырех принципов комплексного обучения: многоплановости, распределения ролей, присвоения компетенции и коллективной ответственности учеников (рис. 7.4).

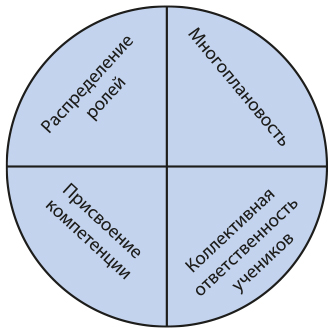
Рис. 7.4. Комплексное обучение

Многоплановость

Одноплановые уроки математики, широко распространенные в США, — это уроки, на которых практика ценится превыше всего и цель состоит в правильном выполнении процедур. Такой узкий критерий успеха приводит к тому, что некоторые ученики поднимаются на самый высокий уровень, получая хорошие оценки и похвалу учителя, а другие опускаются на самый низкий, причем большинству учеников известно их место в иерархии. Такие уроки одноплановые, поскольку на них есть только один способ добиться успеха. На многоплановых уроках математики учителя используют все методы работы.

Например, дети выполняют вычисления, а вдобавок задают интересные вопросы, предлагают идеи, устанавливают связи между разными методами, используют много разных форм представления, выстраивают цепочки логических рассуждений и предпринимают много других действий. Математика — широкая и многоплановая дисциплина. В классах, где применяется комплексный метод, учителя оценивают знания учеников по многим аспектам математики. На стенах классных комнат школы Рейлсайд был вывешен такой девиз комплексного обучения:

Никто не может успешно применять все эти методы работы, но каждый может овладеть некоторыми из них.

Во время бесед с учениками, принимавшими участие в нашем исследовании, мы задавали такой вопрос: «Что необходимо для достижения успеха в математике?» 97% детей, которых обучали в соответствии с традиционным подходом, дали один и тот же ответ: «Работать очень внимательно». Это пассивный подход, который ассоциируется с низким уровнем успеваемости (Bransford, Brown, & Cocking, 1999). Когда мы задали этот же вопрос на уроках в Рейлсайд, дети назвали целый ряд методов работы:

• постановка хороших вопросов;

• изменение формулировки задач;

• объяснение;

• использование логики;

• обоснование методов;

• использование развивающих материалов;

• установление связи между идеями;

• помощь другим.

Ученик по имени Рико сказал: «В средних классах мы просто отрабатывали математические навыки. Но здесь все работают вместе, стараются помогать другим и получать помощь. Это позволяет совершенствовать навыки общения, математические навыки и навыки логического мышления» (ученик Рейлсайд, год 1-й).

Рико рассказал нам о той широте математики, которую он испытал на своем опыте. Ученица по имени Жасмин добавила: «На уроках математики приходится взаимодействовать со всеми, разговаривать с ними и отвечать на их вопросы. Нельзя просто сказать: “Вот учебник, посмотри на числа и разберись во всем”». Когда мы спросили Жасмин, чем можно объяснить тот факт, что уроки математики отличаются от остальных, она сказала: «Это не один способ сделать что-то. Тут все интерпретируют по-своему. Это не только один ответ. Есть много способов все понять. К тому же возникает вопрос: “Почему это работает?”» (ученица школы Рейлсайд, год 1-й). Жасмин подчеркивает социальный и интерпретативный характер математики, когда ученики выходят за рамки учебника и чисел, чтобы осмыслить концепции, проанализировать разные подходы и обосновать ход своих мыслей, отвечая на важный вопрос «Почему это работает?»

В школе Рейлсайд учителя разработали многоплановые занятия с учетом многих аспектов. Это стало возможно благодаря постановке содержательных задач, которые учителя обозначили как задачи, заслуживающие внимания всей группы. Их трудно решить в одиночку, они требуют вклада разных членов группы.

Лани Хорн определяет задачи, заслуживающие внимания всей группы, как «задачи, которые иллюстрируют важные математические концепции, допускают разные формы представления, опираются на эффективное использование коллективных ресурсов группы и имеют несколько возможных решений» (Horn, 2005, p. 22). В примерах 7.1 и 7.2 приведены задачи, которые можно считать заслуживающими внимания группы (они взяты с сайта nrich.maths.org). Полное их описание можно найти в приложении.

ПРИМЕР 7.1. СОРТИРОВКА ЧИСЕЛ

Как насчет того, чтобы решить простую головоломку?

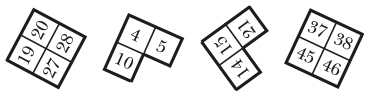
Эта задача предназначена для работы в группах из четырех человек. (Примечания учителей и их идеи по поводу расширения задачи можно найти здесь: http://nrich.maths.org/6947&part=note.)

1. Есть два пазла, которые учитель может распечатать для вас (см. ниже). Сложите каждый, а затем выложите все фрагменты на расчерченные квадраты, которые также можно распечатать.

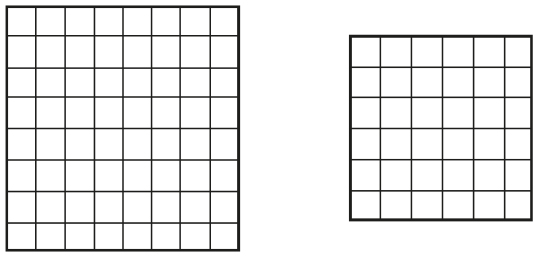
2. Положите меньший квадрат на больший любым удобным для вас способом, чтобы ячейки совпадали. (Возможно, вам будет легче сделать это, если вы скопируете числа, расположенные на меньшем квадрате, на кальку.)

3. Проанализируйте, что произойдет, когда вы сложите числа, расположенные друг над другом.

4. В своей группе проанализируйте все идеи, которые у вас появятся.

Когда вы рассмотрите все 36 комбинаций, вам, вероятно, нужно будет задать вопрос: «Интересно, что произойдет, если мы…» Внесите одно небольшое изменение, проанализируйте этот вариант, а затем сравните два набора результатов.

Возможно, вы захотите задать вопрос: «Почему…»

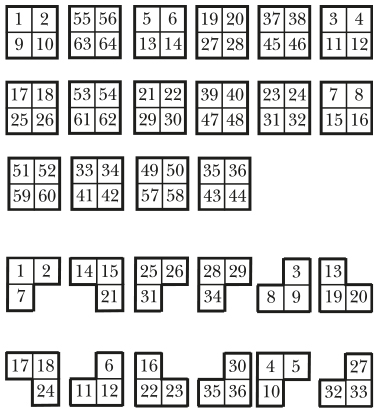
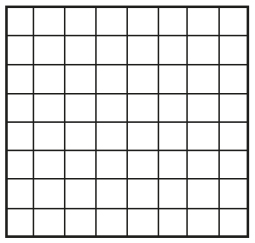
Источник: NRICH (http://nrich.maths.org/6947).

ПРИМЕР 7.2. РАСТУЩИЕ ПРЯМОУГОЛЬНИКИ

Представьте себе прямоугольник площадью 20 см².

Какими могут быть длина и ширина этого прямоугольника? Перечислите минимум пять разных комбинаций.

Представьте себе, что вы увеличили прямоугольник вдвое.

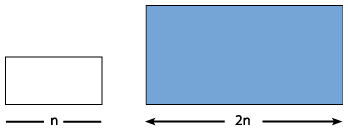
Назовите размеры увеличенного прямоугольника и найдите его площадь. На что вы обратили внимание?

Попробуйте начать с прямоугольника с другой площадью и увеличить его вдвое. На что вы обратили внимание теперь?

Можете ли вы объяснить, что происходит?

Что произойдет с площадью прямоугольника, если вы увеличите его в 3, 4 или 5 раз? Что произойдет с площадью прямоугольника, если вы увеличите его в дробное количество раз?

Что произойдет с площадью прямоугольника, если вы увеличите его в k раз?

Объясните и обоснуйте выводы, к которым вы пришли.

Применимы ли эти выводы к другим двумерным фигурам, кроме прямоугольника?

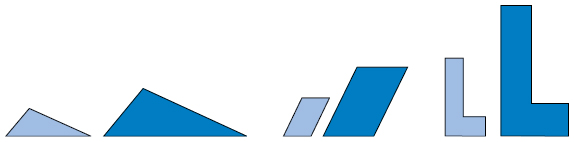
Теперь проанализируйте, что произойдет с площадью поверхности и объемом различных прямоугольных параллелепипедов, если увеличить их в разное количество раз.

Объясните и обоснуйте выводы, к которым вы пришли.

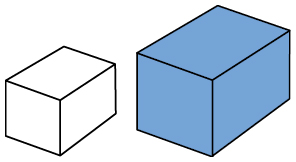
Применимы ли эти выводы к другим объемным фигурам, кроме прямоугольного параллелепипеда?

Источник: NRICH (http://nrich.maths.org/6923).

Пример 7.3 — задание из школы Рейлсайд, где учителя впервые поставили ученикам задачи на линейную функцию (они называют их схемами формирования горок), которые отображали определенную форму представления, и предложили им определить, какой будет, скажем, горка № 10.

ПРИМЕР 7.3. ЗАДАЧА НА ЛИНЕЙНУЮ ФУНКЦИЮ

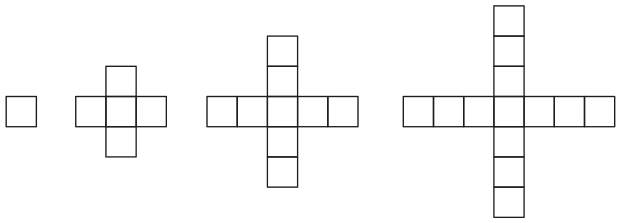
Как растут эти фигуры?

Можете ли вы определить, какой будет фигура на шаге 100?

Какой будет фигура на шаге n?

Одни группы могли представить ответ на этот вопрос в геометрической форме, другие — в числовой, с помощью таблицы из двух столбцов, а третьи — в алгебраической. После того как ученики рассказывали о своих решениях, учителя задавали вопрос: «Кто-нибудь понял это иначе?»

Позже учителя Рейлсайд начали давать более сложные и интересные задания, в рамках которых предоставлялась не вся необходимая информация и ученикам приходилось вместе работать над воссозданием отсутствующих элементов таблицы, графика, уравнения и геометрического представления закономерности, как показано на рис. 7.5.

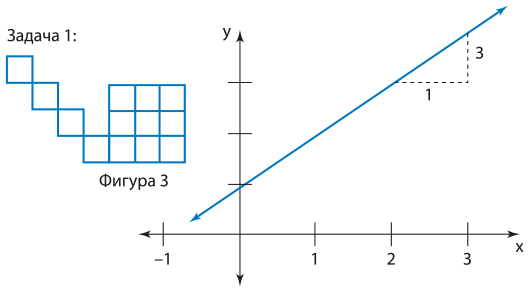
Рис. 7.5. Задача CPM

Более подробная информация об этих и других задачах, которые используются в школе Рейлсайд, можно найти в книге, которую написали ее учителя (Nasir et al., 2014). Многие задачи такого рода представлены в модуле курса CPM[18] под названием Connections («Связи»). В свое время учителя Рейлсайд преподавали математику в рамках традиционных методов в группах, сформированных по принципу успеваемости, но многие ученики не справлялись с этим предметом.

Учителя Рейлсайд не считали, что эти неудачи обусловлены недостатками самих учеников, хотя многие дети поступили в школу с объемом знаний по математике на уровне второго класса. Они подали заявку на грант, который позволил им все лето заниматься планированием новой учебной программы и разработкой нового подхода. Эти учителя уже знали о комплексном обучении, поэтому отказались от формирования классов по успеваемости и разработали вводный курс алгебры, который должны были пройти все новички-старшеклассники. Они создали курс алгебры, который был глубже, чем традиционный, чтобы дать увлекательный опыт всем детям, даже уже изучавшим алгебру. Поскольку учителя Рейлсайд были глубоко привержены идее равенства и совместного обучения, они разработали и внедрили программу, которая открывала ряд возможностей для изучения математики. Стандартные учебники обычно организованы вокруг таких математических методов, как построение графиков линейных функций или разложение многочленов на множители. Учителя Рейлсайд организовали свою программу вокруг таких важных концепций, как «Что такое линейная функция?» Они не составляли задачи; они взяли глубокие, концептуальные задачи по математике из опубликованных учебных программ, таких как College Preparatory Mathematics — CPM («подготовительный курс математики для поступления в колледж») и Interactive Mathematics Program — IMP («программа интерактивного изучения математики»). Кроме того, они решили представлять алгебру с помощью не только рисунков, но и различных предметов, включив в учебную программу специальные развивающие материалы, которые используются для осмысления алгебраических концепций (Picciotto, 1995).

Основным элементом курса алгебры, а впоследствии и других курсов, которые преподавались в Рейлсайд, было множество форм представления: ученикам часто предлагали представить свои идеи разными способами, например в виде слов, графиков, таблиц, символов и диаграмм. Кроме того, детям советовали использовать метод цветового кодирования, представляя каждую идею своим цветом — например, использовать один и тот же цвет для отображения оси x в выражении, диаграмме, на графике, в таблице и текстовом описании (пример 7.4).

ПРИМЕР 7.4. ЗАДАЧА НА МАТЕМАТИЧЕСКУЮ ФУНКЦИЮ

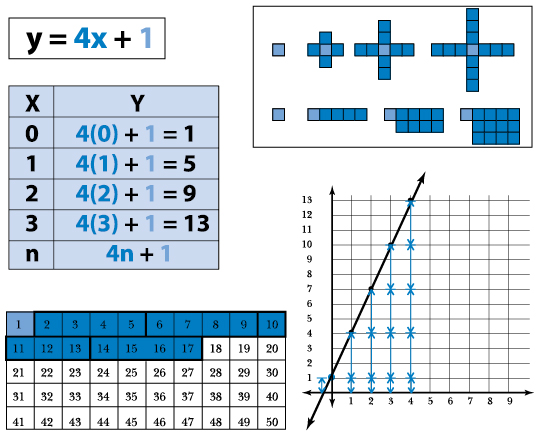
Многоплановый характер уроков в Рейлсайд способствовал тому, что ученики этой школы начали добиваться больших успехов. Проанализировав причины повышения уровня успеваемости в этой школе, мы поняли, что дело было в большем количестве способов добиться успеха.

Учителя Рейлсайд оценивали знания учеников по многим аспектам, а также использовали многофакторную систему оценки (см. главу 8). Стандартные тесты, которые ученики должны были сдавать по требованиям штата Калифорния, не предусматривали оценку знаний в соответствии с многоплановым подходом, но школьники все равно показали очень высокие результаты, потому что научились добиваться успеха на уроках и не боялись математики. Кроме того, к моменту сдачи тестов штата ученики уверенно владели навыками решения задач и были готовы ответить на любой вопрос. Результаты тестирования школьников Рейлсайд по математике были выше, чем по другим предметам (что очень необычно), а сама школа превзошла все остальные школы округа по математике, хотя и была расположена в районе с самым низким уровнем доходов населения.

Во время одного урока алгебры, на котором я присутствовала, ученикам задали как всегда сложную и интересную задачу с краткими инструкциями. Им предложили воспользоваться математическими инструментами, например таблицами с двумя столбцами и графиками, чтобы составить уравнение вида y = mx + b, позволяющее вычислить длину шнурков для ботинок разных размеров (пример 7.5).

ПРИМЕР 7.5. ШНУРКИ

Шнурки какой длины нужны для ботинок разных размеров?

Проанализируйте соотношение между длиной шнурков и размером ботинок.

Составьте уравнение вида y = mx + b, которое поможет башмачнику определить длину шнурков, подходящих ботинкам разных размеров.

Учительница предложила группам учеников поработать с настоящими шнурками, предоставленными одним из членов группы. Она сформулировала задачу, сообщив ученикам, что существует много способов решения этой задачи, а успешная работа над ней потребует правильной коммуникации между членами группы: все должны выслушивать мнение других и давать друг другу возможность обдумать свою работу. Кроме того, учительница объяснила, что ученики получат более высокую оценку за эту задачу, если проиллюстрируют и объяснят свою работу несколькими способами.

Как и в случае многих математических вопросов, для многих учеников самым трудным было начало: нужно было понять, с чего начать. Им предложили составить уравнение, которое поможет купить шнурки. Это открытая постановка задачи, позволяющая самостоятельно определить, что в их уравнении могут быть представлены такие переменные, как число отверстий для шнурков и длина, необходимая для того, чтобы завязать бант. Кроме того, нужно было определить, что переменная y должна представлять в уравнении искомую длину шнурков.

Наблюдая за уроком, я заметила, что многие группы не знали, с чего начать. Мальчик из одной группы сразу заявил: «Я этого не понимаю», а другой согласился с ним: «Я не понимаю вопрос». В этот момент девочка из этой же группы предложила мальчикам еще раз прочесть вопрос вслух. Один мальчик спросил остальных: «Как этот ботинок связан с уравнением?» Другой предложил определить длину своих шнурков. Члены группы начали измерять длину завязки, и в этот момент один мальчик сказал, что им нужно учесть количество отверстий для шнурков. Группа продолжила работу; дети помогали друг другу, задавая вопросы, которые должны была проанализировать группа.

Я наблюдала много подобных ситуаций, когда ученики смогли приступить к решению задачи, подбадривая друг друга, перечитывая задание и задавая друг другу вопросы. Им предлагали прочесть задачу вслух, а когда они не могли двигаться дальше — задавать друг другу вопросы такого рода.

• Что подразумевает этот вопрос?

• Как можно изменить формулировку этого вопроса?

• Каковы основные элементы этой задачи?

В Рейлсайд учителя использовали такой подход: поставить группам задачу, а когда все закончат работу, задать дополнительный вопрос для оценки понимания. Благодаря вопросам, а также поддержке учителей (например, те предлагали иначе сформулировать задачу) ученики научились задавать такие же полезные вопросы друг другу. Вскоре после того, как они начали измерять длину завязок и размышлять о зависимости между ней и количеством отверстий для шнурков, повысился уровень вовлеченности всего класса. Это было обусловлено рядом факторов.

• Работа учителя, который обеспечил продуманную постановку задачи и ходил по классу, задавая ученикам вопросы.

• Сама задача, которая была достаточно открытой и увлекательной, чтобы разные ученики смогли внести свой вклад в ее решение.

• Многоплановость занятия, в ходе которого приветствовались разные способы работы: постановка вопросов, построение диаграмм и выдвижение гипотез.

• Предложение использовать в работе над задачей предмет и идею из реального мира.

• Высокий уровень коммуникации между детьми: они научились поддерживать друг друга, задавая вопросы.

Метод групповой работы используют многие кафедры математики, но они не добиваются таких же высоких показателей успеха учеников и того уровня эффективности работы, который мы видели в Рейлсайд. Одна из причин успеха учеников этой школы состоит в том, что в ней преподают и высоко ценят многоплановую математику, а также учат помогать друг другу.

Распределение ролей

Когда учеников распределили по группам, каждому из них выделили роль в своей группе. В примере 7.6 показан рабочий лист с описанием ролей, который выдается ученикам.

ПРИМЕР 7.6. РАСПРЕДЕЛЕНИЕ РОЛЕЙ В ГРУППЕ — США

Фасилитатор

• Позаботьтесь о том, чтобы ваша группа прочла эту карточку, прежде чем приступать к заданию. «Кто хочет прочесть? Все поняли, что нужно делать?»

• Обеспечивайте сплоченность группы. Позаботьтесь о том, чтобы были услышаны идеи каждого. «Кто-то понял это иначе? Мы готовы двигаться дальше?» Убедитесь, что каждый член группы может объяснить свои идеи.

Секретарь (составитель отчета)

• Ваша группа должна структурировать полученные результаты. Необходимо, чтобы они отражали идеи всех участников и были упорядоченными. Используйте разные цвета, стрелки и другие инструменты, передающие суть математических концепций, аргументов и связей. «Как нам проиллюстрировать эту идею?» Будьте готовы участвовать в совещании с учителем.

Ответственный за ресурсы

• Получите материалы, необходимые вашей команде.

• Убедитесь, что все вопросы требуют командной работы.

• Когда ваша команда закончит работу, позовите учителя, чтобы проанализировать вместе с ним результаты.

Капитан команды

• Напоминайте своей команде о необходимости обосновывать все математические утверждения и искать связи между ними. «Почему вы в этом так уверены? Как это связано с?..»

• Не допускайте никаких разговоров вне группы!

Когда я представила комплексный метод учителям в Англии, они изменили некоторые роли, потому что хотели, чтобы те звучали по-британски и чтобы в них была меньше выражена иерархия. В примере 7.7 показана система распределения ролей, которую предложили английские учителя.

ПРИМЕР 7.7. РАСПРЕДЕЛЕНИЕ РОЛЕЙ В ГРУППЕ — ВЕЛИКОБРИТАНИЯ

Организатор

• Обеспечивайте сплоченность группы и ее сфокусированность на решении задачи; позаботьтесь о том, чтобы никто не разговаривал с участниками других групп.

Снабженец

• Вы единственный человек, который может покинуть свое место, чтобы найти для группы линейки, калькуляторы, карандаши и другие инструменты.

• Убедитесь, что все готовы к работе, прежде чем звать учителя.

Обеспечивающий понимание

• Позаботьтесь о том, чтобы участники группы поняли все идеи.

• Если вы не понимаете идею, спросите того, кто ее предложил, а если понимаете, убедитесь, что остальные тоже ее понимают.

• Позаботьтесь о том, чтобы все важные детали ваших разъяснений были записаны.

Обеспечивающий вовлеченность

• Позаботьтесь о том, чтобы были выслушаны идеи каждого члена группы; предложите другим членам группы внести свои предложения.

Распределение ролей — важная часть комплексного обучения. Оно дает каждому ученику возможность выполнить свою функцию и стимулирует ответственность. Как показывает пример Великобритании, учителя могут адаптировать эти роли к нуждам своих классов.

В классах, которые занимаются по комплексному методу, плакат со схемой распределения групп и ролей размещается на стене. Ученики распределяются по группам и получают роли в случайном порядке.

Раз в несколько недель ученикам предлагают изменить распределение групп и ролей. Во время урока учителя время от времени акцентируют внимание на разных ролях. Например, в самом начале они напоминают фасилитаторам о необходимости помочь ученикам проверить ответы, показать свою работу или задать вопросы.

Все учителя знают, как трудно заставить учеников выслушать их, если те уже начали работу в группах и с воодушевлением обсуждают математические вопросы. Но учителям часто нужно дать ученикам новую информацию или придать групповой работе новое направление.

В случае комплексного подхода учителя не пытаются успокаивать класс. Они вызывают секретарей (составителей отчетов) на совещание. Те приходят на мероприятие, где учитель предоставляет им информацию, которую каждый из них передаст своей группе. Такой подход не только помогает учителю, но и возлагает на учеников ответственность, которая придает им больше уверенности в своих силах. Распределение ролей в рамках комплексного обучения стало неотъемлемой частью взаимосвязанной системы, которая действовала на уроках в школе Рейлсайд и в которой у каждого была важная работа и ученики научились полагаться друг на друга.

Присвоение компетенции

Присвоение компетенции — интересный и тонкий подход, который рекомендуется использовать в системе комплексного обучения. Учитель повышает статус учеников, которые, по его мнению, имеют низкий статус в группе — например, похвалив их за то, что они сказали или сделали нечто имеющее интеллектуальную ценность, а также обратив на это внимание всего класса. В частности, учитель может попросить ученика представить свою идею или в присутствии всего класса похвалить его за выполненную работу.

Я не понимала метод присвоения компетенции до конца, пока не увидела его в действии. Однажды во время визита в Рейлсайд я наблюдала за работой группы из трех учеников. Когда подошел учитель, тихий мальчик-славянин невнятно что-то сказал двум другим членам группы — веселым и активным латиноамериканским девочкам, которые направляли работу группы. Вот что заявил Иван: «Эта задача похожа на предыдущую, которую мы решали». Учитель, который подошел к столу этой группы, сразу обратил внимание на эти слова: «Иван, это очень важная мысль; задача действительно похожа на предыдущую, и мы должны подумать о том, что общего есть у этих двух задач и чем они отличаются». Затем, когда девочки предложили ответ на один из вопросов учителя, он сказал: «Это же похоже на идею Ивана; вы развиваете ее». Учитель повысил статус вклада Ивана, который почти наверняка был бы потерян без его вмешательства. Было заметно, как Иван выпрямился и подался вперед, когда учитель похвалил его идею, а затем напомнил девочкам о ней. По рекомендациям Элизабет Коэн (Cohen, 1994), которая разработала метод комплексного обучения, если обратная связь с учениками призвана решить проблему статуса, она должна носить публичный, интеллектуальный и конкретный характер, а также быть связанной с задачей группы. Публичность обратной связи крайне важна, поскольку другие ученики узнают, что данный ученик предложил идею; интеллектуальность обратной связи гарантирует, что она представляет собой один из аспектов математической работы; конкретность обратной связи означает, что ученики точно знают, что именно хвалит учитель.

Ответственность учеников за обучение друг друга

Формирование ответственности за обучение друг друга — важный элемент справедливых результатов, полученных в школе Рейлсайд, а также центральный элемент метода комплексного обучения. Многие школы используют групповую работу в расчете на то, что ученики смогут сами развить ответственность друг за друга, но эта задача пока не решена. В Рейлсайд учителя применяли много разных методов, чтобы помочь школьникам научиться хорошо работать вместе и ощущать ответственность друг за друга. Одно из важных решений, принятых учителями этой школы, состояло в том, чтобы в самом начале первого года обучения потратить 10 недель первого курса алгебры на обучение детей методам эффективной групповой работы. В этот период ученики занимались математикой, но она была второстепенной целью учителей. Главным для них было обучить школьников эффективно работать в группах. Любой, кто посещал занятия в школе Рейлсайд после этого 10-недельного периода, видел, что такое вложение времени полностью оправдывало себя: ученики поддерживали уважительный диалог, выслушивали друг друга и развивали идеи друг друга.

Обучая группы, я тоже сначала уделяю какое-то время тщательной разработке правил уважительного общения и выслушивания мнений. Перед началом занятий математикой я даю членам группы такое задание: вместе обсудить, какие слова или действия других в процессе общей работы над заданиями по математике им нравятся или не нравятся. Мы вместе делаем два больших плаката: на одном записано все, что нравится группе, а на другом — что не нравится. Затем мы вешаем их на стену. В списке действий, которые членам группы не нравятся, обычно фигурирует многое из того, что я тоже не хотела бы допускать: например, когда один ученик выполняет задание и сообщает ответ остальным, или когда ученики начинают вести себя высокомерно и говорят нечто вроде: «Это просто», или когда кого-то исключают из обсуждения. Я пришла к выводу: когда ученики сами анализируют положительные и отрицательные аспекты группового обсуждения и составляют свои списки, они более вдумчиво относятся к способам взаимодействия в группах. Плакаты висят на стене, а я время от времени напоминаю ученикам и группам о наших правилах.

Кроме того, в начале урока я объясняю ученикам, что для меня важно. Я говорю им, что не вижу особой ценности в скорости или спешке в изучении математики; я ценю людей, которые показывают, как они размышляют над математикой и как важно выслушивать мнения других и относиться друг к другу с уважением. В главе 9 я расскажу о замечательном виде деятельности, который помогает научиться эффективно работать в группах.

Учителя Рейлсайд стимулировали групповую ответственность, задавая одному из членов группы вопрос по математике, имеющий отношение к работе группы. Он всегда носил концептуальный характер, и на него мог ответить только тот, кому его задали. Ученика выбирали случайным образом, другим не разрешалось ему помогать. Если ученик не мог ответить на вопрос, учитель отходил, сказав, что нужно добиться понимания материала всеми членами группы. Затем возвращался и снова задавал этот вопрос тому же ученику. За это время группа должна была помочь участнику изучить необходимый материал. В приведенном ниже интервью две девочки, Гита и Брианна, напрямую связывают свои представления о математике и обретенную ответственность с этим действием учителя.

Интервьюер: Изучение математики — индивидуальный или социальный процесс?

Г.: И то и другое. Если ты что-то понимаешь, нужно объяснить это другим. Иногда нам дают общую задачу, и мы все должны разобраться с ней. Так что, думаю, и то и другое.

Б.: Мне кажется, что и то и другое. Ведь необходимо самому знать материал, чтобы объяснить его другим в процессе общей работы. Ведь никогда не известно, кого из четырех выберет учительница. И все зависит от того, чтобы один человек, которого она выберет, получил правильный ответ. (Школа Рейлсайд, год 2-й.)

Ученицы из представленного выше фрагмента интервью указали на прямую связь между тем, что учителя предлагают любому члену группы ответить на вопрос, и ответственностью за свою группу. Кроме того, они раскрывают интересную социальную установку в отношении математики, заявляя, что знать изучаемый материал необходимо не для того, чтобы быть лучше остальных, а для того, чтобы помочь другим.

Учителя школы Рейлсайд использовали для стимулирования групповой ответственности еще один метод. Он может вызвать у кого-то возмущение, но на самом деле позволяет донести до членов группы мысль о том, что они несут ответственность друг за друга. Время от времени учителя проводили так называемые групповые тесты. Ученики сдавали тесты индивидуально, но учителя принимали только один (выбранный случайным образом) лист с заданиями от каждой группы и ставили оценку, которая становилась оценкой всех членов группы. Для учеников это был четкий сигнал, напоминающий им о необходимости позаботиться о том, чтобы все члены группы поняли соответствующий материал.

Ученики пришли в школу Рейлсайд, имея за плечами восьмилетний опыт индивидуальной работы и воспринимая математику как индивидуальный, конкурентный вид деятельности. В Рейлсайд они узнали о другой математике и других целях обучения и быстро адаптировались к ним без особых сложностей. Вскоре после начала учебы школьники начали воспринимать математику как общее занятие, в котором главное — помогать друг другу и работать вместе. В первые месяцы сильные ученики жаловались нам на то, что им постоянно приходится объяснять свою работу, но через несколько месяцев изменилось даже их отношение. Эти ребята начали ценить то, что они работают в группах и могут объяснить ход своих мыслей, поскольку поняли, что это помогает им самим осмыслить изучаемый материал.

Имельда, одна из девочек, которая изучала анализ в последние годы нашего курса, так описала то, как социальная ответственность помогла ей.

Думаю, люди воспринимают это как ответственность. Думаю, до этого они доросли после стольких уроков по математике. Может, в девятом классе ты думаешь так: «О боже, не хочу им помогать, хочу сделать свою работу, почему мы должны проходить этот групповой тест?» Но когда ты начинаешь изучать углубленный курс анализа, ты уже думаешь так: «О, нужно пройти групповой тест, прежде чем сдавать свой». Так что чем больше ты изучаешь математику и чем больше учишься, тем больше ценишь то, что имеешь: «Слава богу, я в группе!» (Имельда, школа Рейлсайд, год 4-й.)

Хотя учителя Рейлсайд и не ставили такую цель, по результатам статистического анализа мы обнаружили, что формирование разнородных групп и комплексный подход принесли самую большую пользу ученикам, которые изначально относились к числу сильных. Их обучение ускорилось в большей степени, чем у других учеников школы; кроме того, они добивались гораздо более высоких результатов в учебе по сравнению с подростками, которые проходили углубленные курсы в других школах, — отчасти потому, что объясняли свою работу, благодаря чему повышался уровень осмысления материала, а также потому, что их работа была более многоплановой. Многие из этих учеников пришли в Рейлсайд, обладая хорошими навыками быстрых вычислений и выполнения процедур, и необходимость расширить и углубить работу над математикой во многом способствовала повышению их успеваемости.

Кроме того, у учеников Рейлсайд сформировались более широкие представления о роли разных учеников. Они начали понимать, что каждый может внести свой вклад в решение задачи. По мере того как подход к обучению становился все более многоплановым, у них сформировалось многоплановое восприятие друг друга и они начали ценить разные способы понимания и осмысления математических идей, которые другие привносили в решение задач. Вот рассуждения еще двух учениц этой школы.

Интервьюер: Как вы думаете, что необходимо, чтобы добиться успеха в математике?

А.: Способность работать с другими людьми.

Э.: Открытость мышления и умение выслушивать идеи других.

А.: Необходимо прислушиваться к мнению других, потому что ты можешь ошибаться.

Э.: Ты можешь ошибаться, потому что есть много разных способов все понять.

А.: У каждого свой способ выполнения заданий, всегда можно найти разные способы что-то понять, что-то выяснить.

Э.: Кто-нибудь предлагает какой-то способ что-то сделать, и мы всегда думаем так: «Надо же, не могу поверить, что ты мог такое придумать». (Аяна и Эстель, школа Рейлсайд, год 4-й.)

Во время интервью ученики рассказали нам, что благодаря подходу школы Рейлсайд они научились ценить представителей разных культур, классов и пола.

Р.: Знаете, я люблю эту школу. В паре километров от нас есть другие, совсем непохожие школы — они разделены на расовые группы и все такое. А в этой каждого принимают как личность и никто не смотрит на цвет кожи.

Интервьюер: Этому способствует подход к математике или это влияние школы в целом?

Д.: Группы по математике помогают объединить детей.

Р.: Да. Когда переходишь из одной группы в другую, то общаешься с большим количеством людей, чем когда сидишь в классе на отведенном тебе месте, где тебя видят только те, кто вокруг, и ты не знаешь тех, кто в другом конце класса. На уроках математики ты должен говорить, заявлять о том, что ты чего-то не понимаешь, или рассказывать о том, что ты изучаешь. (Роберт и Джон, школа Рейлсайд, год 4-й.)

В школе Рейлсайд учителя математики высоко ценили равенство, но не использовали материалы учебных программ, поднимающие вопросы пола, культуры или класса, как кое-кто рекомендовал (Gutstein, Lipman, Hernandez, & de los Reyes, 1997). Они учили детей ценить различные подходы к математике. По мере того как занятия становились более многоплановыми, школьники учились ценить идеи разных учеников.

Многие родители беспокоятся о перспективах сильных учеников в смешанных группах, считая, что слабые ученики снизят общую успеваемость. Но обычно такого не происходит. В образовательной системе США сильные ученики часто получают такой статус, потому что умеют быстро выполнять процедуры. Многие из них не научились глубоко анализировать идеи, объяснять свою работу или рассматривать математическую задачу с разных точек зрения, поскольку им никто никогда не предлагал этого. Работа в группах идет им на пользу, поскольку позволяет глубже осмыслить материал и обосновать свое мнение, лучше поняв предмет. Присутствие отстающих не снижает общий уровень достижений группы; уровень дискуссий повышается до уровня мышления самых сильных учеников. Если бы в состав групп входили ученики с одинаковым уровнем успеваемости, это не принесло бы пользы ни сильным, ни слабым.

Ученицы Рейлсайд поняли, что у каждого свой уровень знаний, и научились ценить сильные стороны разных учеников, как отметил Зак.

У каждого свой уровень, и это отлично: ведь все постоянно учат друг друга и помогают друг другу.

Два метода, которые я считаю особенно важными для обеспечения равенства и которые сыграли центральную роль в формировании ответственности учеников друг за друга, — обоснование и рассуждение. В школе Рейлсайд ученики должны были постоянно обосновывать свои ответы и аргументировать выбор методов. Тому есть много веских причин, учитывая, что обоснование и рассуждение — по сути математические методы (Boaler, 2013c), при этом играющие интересную и особенную роль в обеспечении равноправия.

Представленный ниже фрагмент взят из беседы с Хуаном, который был в то время одним из самых слабых в классе. Вот что он рассказал о том, как ему помогли методы обоснования и рассуждения.

Большинство из них просто знают, что делать и всё такое. Сначала я думаю: «Зачем мне это задали?» — а потом выполняю свою работу и сравниваю ее с их работой. Их работа совсем другая, потому что они знают, что делать. И я говорю: «Дай списать»; я спрашиваю: «Почему ты сделал так?» А потом говорю: «Я не понимаю, почему ты получил такой ответ». Иногда ответ прост… «Да, он прав, а ты ошибся». Но почему?

Хуан четко дал понять, что ему помог метод обоснования и ему по душе возможность подтолкнуть других к тому, чтобы они вышли за рамки ответов и объяснили, почему они дали их, иными словами — порассуждали. В школе Рейлсайд учителя делали особый упор на том, что у каждого есть две важные обязанности.

Всегда помогайте, когда нужна ваша помощь, и всегда просите о помощи, когда она нужна вам.

Обе эти обязанности играли важную роль в обеспечении равенства, а обоснование и рассуждение стали полезными элементами обучения широкого круга школьников.

Было бы трудно провести целые годы на уроках в Рейлсайд, не обратив внимания на то, что дети учатся общаться друг с другом более уважительно, чем в обычных школах, а этнические группировки (вроде тех, о которых говорили Роберт и Джон) на уроках математики менее выражены, чем на большинстве других уроков. На занятиях математикой школьников учили ценить вклад разных учеников из разных культурных групп и с разными личными качествами и взглядами. У меня создалось впечатление, что благодаря этому школьники научились чему-то очень важному — тому, что сослужит им и другим добрую службу в будущем, при взаимодействии с другими членами общества. Я назвала это отношенческим равенством (Boaler, 2008). Это такая форма равенства, в которой главное — не одинаковые результаты тестов, а уважение и забота о других независимо от их культуры, расы, религии, пола и других характеристик. Принято считать, что ученики научатся с уважением относиться к разным людям и культурам, если будут обсуждать эти вопросы или читать разноплановые книги на уроках литературы или естествознания. Я считаю, что все предметы могут внести свой вклад в обеспечение равенства, и математика — которую часто считают самой абстрактной дисциплиной, весьма далекой от вопросов ответственности за обеспечение культурной или социальной осведомленности, — может внести в это важный вклад. Уважительные отношения между учениками школы Рейлсайд независимо от культуры и пола стали возможными только благодаря подходу к преподаванию математики, при котором в процессе решения задач учитываются разные идеи, методы и мнения.

Резюме

Справедливый подход к преподаванию, ориентированный на мышление роста, сложнее традиционного, при котором учитель объясняет материал и дает короткие задания для практики. Он подразумевает преподавание широкой, открытой, многоплановой математики, обучение ответственности друг за друга и объяснение сути мышления роста. Это самый важный и приносящий самое большое удовлетворение подход, который может использовать учитель математики: наблюдая за увлеченными и успешными учениками, учителя ощущают удовлетворение и прилив энергии. Мне посчастливилось работать со многими учителями, которые привержены идее равенства и придерживаются подхода к преподаванию и разделению на группы, ориентированного на мышление роста, даже если не используют именно эти слова. В этой главе представлены многие из тех идей, о которых я узнала за многие годы работы и исследований с участием этих очень успешных учителей. Свою любимую стратегию стимулирования эффективной групповой работы я оставила для главы 9, где пойдет речь обо всех нормах и методах, которые я рекомендую использовать для проведения уроков математики, ориентированных на мышление роста.