Глава 8. Оценка для мышления роста

Комплексный подход к математике, который используют дети, вызывает у меня восхищение. Ученики задают вопросы, визуализируют идеи, представляют задачи в графическом виде, обосновывают выбор методов и выстраивают цепочки рассуждений разными способами. Но в последние годы все эти тонкие и сложные особенности понимания математики сводятся к числам или буквам, по которым судят о том, чего стоит ученик. Учителей вынуждают проводить тесты и ставить оценки в нелепых и губительных масштабах; ученики начинают оценивать себя (и математику) в буквах и числах. Такое примитивное представление не только не позволяет правильно охарактеризовать знания детей, но и часто дает ложную картину.

В США ученики сдают так много тестов (особенно по математике), что это выходит за рамки разумного. Много лет уровень знаний учеников оценивается по узким, процедурным вопросам по математике с несколькими вариантами ответа. Навыки, нужные для сдачи таких тестов, весьма далеки от адаптивного, критического и аналитического мышления, которое необходимо в современном мире и во имя которого такие работодатели, как Google, объявили о том, что их больше не интересуют результаты тестирования учащихся, поскольку они не связаны с успешным выполнением задач на рабочем месте (Bryant, 2013).

Правильные тесты должны оценивать нечто важное. В США много десятилетий тесты оценивали то, что было легко проверить, а не ценные аспекты математики. Учителя вынуждены были преподавать узкую процедурную математику, а не широкую, творческую, развивающую, которая так важна в современном мире. Новая система оценки уровня знаний учеников предлагает другой подход, при котором тесты содержат мало вопросов с несколькими вариантами ответа на выбор и больше способов оценки навыков решения задач. Но такой подход встретил жесткое сопротивление родителей.

Ущерб, который наносит ученикам действующая система оценки знаний, не ограничивается стандартным тестированием. Учителя математики считают необходимым проводить на уроках тесты, которые имитируют стандартные тесты низкого качества, даже если осознают, что оцениваются в них узкие аспекты понимания математики. Учителя тем самым стремятся подготовить учеников к успешной сдаче тестов в будущем. Некоторые, особенно учителя старших классов, проводят тесты каждую неделю или чаще. Регулярные тесты нужны им больше, чем учителям по другим предметам; как правило, они не учитывают негативную роль, которую тесты играют в формировании взглядов учеников на математику и самих себя. Многие знакомые мне учителя математики начинают учебный год или курс с теста, который подает ученикам сильный сигнал в отношении результатов в самом начале. А на самом деле важно подавать ученикам сигналы роста в отношении математики и обучения.

Финляндия — страна с одними из самых высоких в мире результатами международных тестов по математике, но там ученики не сдают никаких тестов в школе. Учителя используют глубокое понимание знаний учеников, полученное в процессе обучения, чтобы отчитаться перед родителями и составить мнение о выполненной работе. В ходе лонгитюдного исследования, которое я проводила в Англии, ученики работали над открытыми проектами на протяжении трех лет (с тринадцати до шестнадцати лет), после чего сдавали государственные стандартные экзамены. Они не сдавали тесты, им не ставили оценки на уроках. Они столкнулись с процедурами оценки уровня знаний с помощью коротких вопросов только за несколько недель до экзамена, когда учителя выдали им экзаменационные листы, которые необходимо было проработать. Несмотря на отсутствие навыков поиска ответов на экзаменационные вопросы или работы в условиях ограничения времени, эти ученики получили гораздо более высокие результаты по сравнению с группой учеников, которые провели эти три года, прорабатывая вопросы, аналогичные вопросам государственного экзамена, и часто сдавая тесты. Ученики школы, в которой большое внимание уделялось развитию навыков решения задач, хорошо сдали стандартный государственный экзамен, потому что их научили верить в свои способности; им дали полезную диагностическую информацию об их обучении, и они поняли, что могут найти ответ на любой вопрос, потому что умеют решать математические задачи.

В рамках своего научного исследования я получила доступ к ученическим работам (по экзаменам GCSE), которые экзаменационная комиссия в Англии держала за семью печатями. Она удовлетворила мою необычную просьбу, признав, что это принесет пользу развитию научного знания. Я провела целый день в затерявшейся среди кабинетов комнате без окон размером со шкаф, записывая и анализируя все результаты. Это было поучительно. Я обнаружила, что ученики, которые работали над открытыми проектами, брались за существенно большее количество заданий, пытаясь решить их независимо от того, узнали ли они задачу или нет. Это важная и ценная практика, которую должны освоить все. Кроме того, эти ученики успешнее справлялись с вопросами, за которые брались, даже если это были вопросы на оценку знания стандартного метода, которому их не учили. Я разделила все вопросы на две категории — процедурные и концептуальные — и обнаружила, что ученики из двух школ получили одинаковые результаты по процедурным вопросам, которые подразумевали простое применение стандартных методов. Ученики школы, работающей на основе проектно-ориентированного подхода, добились гораздо более высоких результатов, отвечая на концептуальные вопросы, которые требуют размышлений. Тот факт, что ученики, которые не сдают тесты в школе, получили лучшие результаты, может показаться парадоксальным. Но новые исследования в области головного мозга и обучения легко его объясняют. Ученики, не имеющие опыта сдачи экзаменов и тестов, могут добиться лучших результатов, потому что обладают мышлением роста, уверены в своих способностях и владеют математическими инструментами для решения задач, которые они готовы применять в любой ситуации.

Современная система оценки очень плохо повлияла на учеников, и это влияние не ограничивается самим тестированием: выставление отметок имеет такой же негативный эффект. Когда ученикам ставят оценки, выраженные в процентах или баллах, им остается только сравнивать свои показатели с оценками других детей, причем половина учеников приходит к выводу, что они хуже остальных. Этот феномен известен как обратная связь, продиктованная эго: разновидность обратной связи, которая, как оказалось, вредит обучению. К сожалению, ученики начинают отождествлять себя с оценками. Они воспринимают баллы не как показатель их работы или того, что им необходимо для достижения успеха, а как показатель того, что они представляют собой как люди. Американские школьники часто говорят о себе «Я ученик уровня A» или «Я ученик уровня D», и это значит, что школьники меряют свою личность оценками. Рей Макдермотт написал очень интересную статью о том, как ребенок попадает в плен необучаемости. Там идет речь о том, как ученику, который размышлял и работал иначе, навесили ярлык, а затем определяли его сущность по этому ярлыку (McDermott, 1993). Я могла бы привести аналогичные аргументы по поводу того, как ученики попадают в плен оценок и баллов за тесты. Школьники называют себя учениками уровня A или D, поскольку выросли в культуре достижений, где придавалось большое значение постоянному тестированию и оценкам, а не настойчивости, смелости и умению решать задачи. Традиционные методы оценки учеников, которые использовались в США десятки лет, были разработаны в менее просвещенную эпоху (Kohn, 2011), когда считалось, что оценки и баллы за тесты будут мотивировать учеников и дадут полезную информацию об успеваемости. Теперь мы знаем, что оценки и результаты тестов скорее лишают мотивации и подают ученикам губительные сигналы, которые приводят к снижению их успеваемости на уроках.

Изучая систему оценок и альтернативы ей, исследователи получали сопоставимые результаты. Многие работы показывают, что оценки снижают успеваемость учеников. Например, Мария Элавар и Лин Корно сравнили разные типы реакции учителей на домашние задания, когда половина учеников получали оценки, а другая — комментарии без них (Elawar & Corno, 1985). Ученики, получавшие комментарии, учились вдвое быстрее контрольной группы, разрыв в успеваемости между мальчиками и девочками исчез, а отношение к учебе улучшилось.

Рут Батлер сопоставила также результаты учеников, которым ставили оценки за работу в классе, с результатами тех, кто получал комментарии без оценок (Butler, 1987, 1988). Так же как и в ходе исследования, которое провели Корно и Элавар, ученики, получавшие комментарии, добивались гораздо больших успехов в учебе. Интересная особенность исследования Батлер состояла в том, что позже она добавила третий вариант — некоторым ученикам ставили оценки и давали комментарии (вроде бы лучшее сочетание вариантов). Но в ходе исследования было установлено, что ученики, которые получали только оценки, либо оценки и комментарии, показали одинаково плохие результаты (поскольку фокусировались на оценках), а существенно лучших добилась группа, которая получала только комментарии. Батлер обнаружила, что ученики пятых и шестых классов как с высокой (лучшие 25%), так и с низкой успеваемостью (худшие 25%) показывали слабые результативность и мотивацию в обоих группах с выставлением оценок, в отличие от учеников, которые получали только комментарии.

После исследования Батлер Каролин Палфри, Фабрицио Бутера и Селин Букс (Pulfrey, Butera, and Buchs, 2011) провели свое и получили схожий результат, снова продемонстрировав, что успеваемость и мотивация учеников, получавших оценки, и учеников, получавших оценки и комментарии, оказалась ниже успеваемости учеников, которые получали только комментарии. Кроме того, исследователи обнаружили, что ученикам достаточно было думать, что они работают ради оценки, — и они уже теряли мотивацию, что приводило к снижению успеваемости.

Переход от оценок к комментариям — важный шаг, позволяющий учителям предложить ученикам удивительный дар: дар знаний и понимания путей совершенствования. Они вполне справедливо тревожатся о том, что такой подход может потребовать больше времени: ведь хорошие учителя всегда уделяют работе гораздо больше времени, чем те часы, за которые им платят. Рекомендую такое решение: меньше заниматься оценкой уровня знаний. Заменив еженедельное выставление оценок периодическими комментариями, учителя могли бы сэкономить время, исключить сигналы об оценках, способствующие укреплению установок на данность, и дать ученикам глубокое понимание предмета, которое поспособствует повышению успеваемости. Чуть ниже приведены отзывы разных учителей, с которыми я работала и которым удалось изменить систему оценки знаний, не вкладывая в это больше времени. Они рассказывают о своей работе и о том, какое влияние она оказала на их учеников.

Гонка в никуда

«Гонка в никуда» — документальный фильм, в котором показано, какой стресс испытывают ученики американских школ. Он вышел в прокат несколько лет назад и получил широкое внимание и признание: в New York Times, например, назвали его обязательным к просмотру. Вскоре после выхода фильм собирал полные залы зрителей в кинотеатрах и школьных залах по всей стране. В нем показано губительное влияние тестов, оценок, домашних заданий и чрезмерной загруженности на здоровье и благополучие учеников. Кампания, развернувшаяся после выхода этого фильма, получила поддержку десятков тысяч педагогов и родителей. Во время просмотра этого фильма я видела, что математика — главный источник стресса и тревог учеников. В нем рассказывается грустная история об одной ученице старшей школы по имени Девон Марвин, которая всегда успешно справлялась с математикой. Это была очень мотивированная девочка, которая воспринимала математику как часть своей личности. Но однажды она получила за тест по математике оценку F и покончила с собой. Для Девон, как и для многих других учеников, оценка по математике означала сигнал не о том, над какой областью ей необходимо поработать на пути к обучению, ориентированному на рост, а о том, что она представляет собой как личность: теперь она стала «ученицей уровня F». Эта мысль оказалась настолько тяжелой для Девон, что она совершила самоубийство.

Оценивая уровень знаний учеников, мы создаем важную возможность. Умело составленные задачи и вопросы в сочетании с четкой обратной связью открывают перед учениками путь к формированию мышления роста, который помогает им понять, что они могут добиться самых высоких результатов в учебе и, что очень важно, как это сделать. К сожалению, большинство систем оценки в школах США делают нечто прямо противоположное, предоставляя ученикам информацию, под влиянием которой многие из них считают себя неудачниками, не способными заниматься математикой. В последние годы я работала с учителями, которые отошли от стандартных тестов с отметками и баллами к оценке, сфокусированной на предоставлении информации, необходимой для успешной учебы, в сочетании с сигналами, ориентированными на мышление роста. Это кардинально изменило атмосферу на уроках. Тревога в связи с математикой, которая раньше была обычным явлением среди учеников, уступила место уверенности в своих силах. Это привело к повышению уровня мотивации, вовлеченности и успеваемости. В этой главе я расскажу о некоторых изменениях, которые необходимо предпринять на уроках, чтобы заменить тестирование, ориентированное на фиксированное мышление, системой оценки, которая ориентирована на мышление роста и расширяет возможности учащихся.

Режиссер фильма «Гонка в никуда» Вики Абелес сняла продолжение под названием «Сверх меры». В процессе работы над фильмом и во время интервью с учениками и родителями из всех уголков США она поняла, что математика — предмет, который больше всего нуждается в переменах и больше, чем другие дисциплины, убивает мечты учеников о колледже и даже окончании средней школы. Именно поэтому Вики посвятила весь новый фильм проблемам в сфере математики. В этом фильме рассказывается о работе, которую на протяжении последних нескольких лет я вела с учителями в школьном округе с очень слабыми результатами по математике. В школьном округе Виста в Сан-Диего, как и во многих других городских районах США, более половины учеников не справлялись с алгеброй, после чего попадали в порочный круг неудач. Но неудачи в математике не ограничиваются самой этой дисциплиной. Количество учеников, которые оканчивают среднюю школу по так называемой программе A — G (включающей в себя обязательные курсы старшей школы), или программе готовности к колледжу, составляет всего 24%. К счастью, в школьном округе Виста работали такие инноваторы, как инспектор Девин Водичка и руководитель направления математики Кэти Уильямс. Они знали о необходимости изменений и были готовы потратить на них время и энергию. Весь следующий год я работала с учителями всех средних школ этого округа над повышением их профессионального уровня в таких областях, как способы эффективного преподавания математики, разделение на группы для достижения успеха и оценка с ориентацией на мышление роста.

Руководитель направления математики этого школьного округа Кэти Уильямс приняла решение о том, что все учителя средних школ округа должны будут работать со мной год, хотят они того или нет. Когда я впервые встретилась с этой группой учителей, у них были разные уровни мотивации к переменам. Я до сих пор помню Фрэнка — человека в возрасте, близком к пенсионному, — не собиравшегося менять модель преподавания, которую он применял на протяжении всей своей трудовой жизни. На нескольких первых занятиях он не проявлял особого энтузиазма. Но постепенно он проникся воодушевлением других учителей и начал понимать важность исследований, о которых я рассказывала. В итоге Фрэнк осознал, что может дать своим ученикам иное, лучшее будущее в математике. Я до сих пор хорошо помню занятие в конце года, когда он ворвался в аудиторию с эмоциональным рассказом, как он вместе с женой все выходные рисовал график на куске ткани во всю стену и каким замечательным был урок математики, на котором он предложил ученикам пройти вдоль него, чтобы понять смысл представленных на нем соотношений. И такое воодушевление появлялось у всех учителей, когда они применяли новые идеи в работе со своими учениками и видели, как повышается их вовлеченность.

Я решительно выступаю в поддержку учителей и знаю, что эпоха закона «Ни одного отстающего» лишила многих из них профессионализма и энтузиазма, поскольку их вынуждали (я специально выбрала именно это слово) использовать методы, которые, как им было хорошо известно, не принесут пользы. Сейчас важная часть моей работы с учителями сводится к тому, чтобы помочь им вернуть чувство профессионализма. Во время занятий по профессиональному развитию, которые я проводила в школьном округе Виста, учителя начинали снова считать себя творцами, способными сформировать среду обучения, наполненную их идеями по поводу творческой, увлекательной математики. Это приносит учителям гораздо большее удовлетворение, поэтому я призываю всех, с кем я работаю, придерживаться именно такого подхода. Я видела, как учителя оживают. Каждый день, который мы проводили вместе, аудитория все больше наполнялась энергией. За год учителя перешли от математики в виде листов с заданиями к математике, основанной на изысканиях; они отказались от деления учеников на группы по успеваемости, получив возможность объяснить всем, что они могут добиться больших успехов в математике. Кроме того, эти учителя стали оценивать работу учеников не с установкой на данность, а с установкой на рост. Такие перемены происходили со многими учителями, с которыми я работала. Для этого нужно относиться к ним как к профессионалам и предлагать использовать свои суждения в сочетании с идеями научных исследований, чтобы обеспечить ученикам положительный опыт обучения и оценки.

В своем новом фильме Вики Абелес и члены ее команды берут интервью у некоторых учеников средней школы школьного округа Виста. Дети рассказывают об изменениях, произошедших в их классах после года обучения учителей на курсах профессионального развития. Одна девочка по имени Делия рассказала о том, как годом ранее получила оценку F за домашнюю работу и из-за этого прекратила дальнейшие попытки чего-то добиться на уроках математики и, как ни странно, на всех остальных уроках в школе. Во время интервью она трогательно говорит: «Увидев F, я почувствовала себя пустым местом. Я не справлялась с предметом, поэтому подумала, что могу провалиться и в других. Я даже не пыталась». Через какое-то время в фильме Делия рассказывает о переменах на уроках математики, а также о том, что теперь она испытывает воодушевление по поводу возможности добиться успеха. «Я ненавидела математику, — говорит она. — Я сильно ее ненавидела, но теперь у меня есть связь с ней, я открыта, я чувствую себя живой, у меня больше энергии».

Тот факт, что Делия использует слово «открытый» в описании своих чувств к математике, перекликается с тем, что я часто слышу от учеников, когда они осваивают математику без неизбежного страха низких оценок. Но дело не только в оценивании. Когда мы преподаем творческую, исследовательскую математику, ученики испытывают сильное ощущение интеллектуальной свободы. Во время интервью с третьеклассниками, которые принимали участие в разговорах о числах на уроках математики (глава 4), я спрашивала, какие чувства вызывают у них разговоры о числах. Ученик по имени Дилан начал так: «Я чувствую себя свободным». Затем он рассказал о том, как оценка различных математических стратегий позволила ему почувствовать, что он может заниматься математикой так, как пожелает, исследовать разные идеи и узнавать что-то новое о числах. Тот факт, что ученики используют слова «свободный» и «открытый», демонстрирует, как важно то, что они занимаются математикой, ориентированной на мышление роста. Значение такого подхода выходит за рамки успеваемости по математике и распространяется на расширение интеллектуального потенциала учеников, которое будет влиять на них на протяжении всей жизни (Boaler, 2015a).

Представления о собственном потенциале, которые формируются у учеников, влияют на их успеваемость и, что не менее важно, на их мотивацию и старание. Именно об этом говорит Делия в фильме. Получив неудовлетворительную оценку по математике, она поставила крест не только на этой дисциплине, но и на остальных предметах, поскольку чувствовала себя неудачницей. Такая реакция — далеко не редкость. Когда ученикам ставят баллы, которые говорят им о том, что у них более низкий рейтинг по сравнению с остальными, они разочаровываются в школе, приходят к выводу, что так и не смогут ничему научиться, и у них формируется комплекс отстающего. Оценки и баллы, которые выставляют ученикам с высокой успеваемостью, наносят такой же вред. Эти дети начинают думать, что относятся к числу «учеников уровня A», и становятся на сомнительный путь обучения с установкой на данность, который вынуждает их избегать трудной работы или сложных задач из страха потерять свой статус. Такие ученики часто приходят в отчаяние, получая оценку B или ниже за любую свою работу.

После недавней презентации перед учителями о влиянии оценок один опытный преподаватель старших классов средней школы подошел поговорить со мной. Он сказал, что работает в старшей школе уже более 20 лет и ставил ученикам оценки вплоть до прошлого года. Он поведал, что такое изменение оказало исключительное влияние на учеников: весь класс превратился в открытое учебное пространство, в котором подростки работают более усердно и добиваются более высоких результатов. Учитель также отметил, что вместо оценок использует систему, в соответствии с которой ученики должны решить как можно больше задач. Когда дети доходили до трудных задач, которые они не могли решить, учитель предлагал им нарисовать линию поперек страницы и решить оставшиеся задачи с помощью учебника. По завершении работы над заданиями ученики вместе обсуждали задания, которые оказались под чертой. Этот учитель сказал, что такая система оценки, которая подавала ученикам замечательные сигналы, ориентированные на мышление роста, дает ему лучшую информацию о математике, которую он преподает, обеспечивая быстрый и легкий способ определить, с какими трудностями столкнулись ученики и что должно стать темой обсуждения на уроке.

В ходе еще одного исследования об оценках Мэтт Диверс обнаружил, что ученики, которым вместо оценок и баллов дают позитивную и конструктивную обратную связь, добиваются более высоких успехов в работе в будущем (Deevers, 2006). К сожалению, он обнаружил также, что чем старше ученики, тем меньше конструктивной обратной связи предоставляют им учителя и тем чаще прибегают к оценкам. Диверс нашел явную и вполне ожидаемую связь между методами оценивания, которые использует учитель, и убеждениями учеников. Причем уровень уверенности учеников в своем потенциале и возможности улучшения результатов неуклонно снижался с шестого по двенадцатый класс (Deevers, 2006). Традиционная культура оценки знаний в старших классах, свойственная учителям математики, убежденным в том, что они должны часто проводить тесты, ориентированные на фиксированное мышление, и выставлять отметки, доминировала на протяжении десятилетий. Именно поэтому мне было особенно приятно услышать историю опытного учителя, который изменил свой подход к преподаванию, создал «открытые» уроки и сразу увидел изменения в мотивации и результатах учеников.

Необходимо, чтобы ученики испытывали воодушевление и интерес к обучению. Тогда их мотивация и успеваемость повысятся. Существует много исследований, посвященных двум типам мотивации. Внутренняя проистекает из интереса к предмету и концепциям, которые вы изучаете; внешнюю обеспечивают мысли о получении более высоких баллов. Поскольку математику десятилетиями преподавали как предмет, ориентированный на результат, самыми мотивированными учениками на уроках являются, как правило, ученики с внешней мотивацией. Один из результатов заключается в том, что высокие оценки и баллы обычно получают именно те, кто позитивно настроен по отношению к математике. Большинство учителей, которые верят в оценки, используют их, убежденные в том, что они мотивируют учеников. Некоторых они и правда мотивируют (тех, кто в любом случае получил бы высокие оценки), но при этом лишают мотивации остальных. К сожалению, внешняя мотивация сильных учеников не приносит пользы в долгосрочной перспективе. Многочисленные исследования показывают, что ученики, у которых формируется внутренняя мотивация, добиваются более высоких результатов, чем ученики с внешней мотивацией (Pulfrey, Buchs, & Butera, 2011; Lemos & Ver?ssimo, 2014), а также что внутренняя мотивация побуждает учеников изучать различные дисциплины на более высоком уровне и продолжать заниматься ими (Stipek, 1993).

Я увидела разницу в последствиях внутренней и внешней мотивации на примере своей дочери, когда она перешла в пятый класс. Моя дочь училась в местной начальной школе, где не ставились оценки и было мало тестов, поэтому до пятого класса она получала только обратную связь по поводу своей работы, благодаря чему у нее была замечательная внутренняя мотивация, за формированием которой я наблюдала, когда она приходила домой и с восторгом рассказывала обо всем, что изучает в школе. В пятом классе у нее был очень квалифицированный учитель, который использовал на уроках содержательные и увлекательные виды деятельности, но выставлял ученикам оценки за всю их работу. Этот учитель сказал мне, что делает это потому, что в местных средних школах оценки выставляются за все и он хочет подготовить детей к этому. Элфи Кон описывает такой подход как BGUTI — better get used to it («к этому надо привыкнуть»). Практика, которая наносит вред ученикам, применяется в школах потому, что, по мнению учителей, ученики непременно столкнутся с такой практикой и надо, чтобы они были готовы к этому. За учебный год пятого класса я увидела очень серьезные перемены в своей дочери, которая внезапно начала заботиться (и беспокоиться) только об оценках. Она перестала уделять внимание концепциям, которые изучала, и постоянно беспокоилась по поводу отметки, которую может получить за свою работу. Элфи Кон (Kohn, 2011) приводит высказывание ученицы Клер, которая описывает аналогичные перемены.

Я помню, как в моей письменной работе впервые появился раздел для оценки… Внезапно вся радость исчезла. Я писала только ради оценки — я больше не исследовала ничего для себя. Я хочу вернуть всё. Будет ли когда-нибудь всё как раньше?

По словам Клер, она утратила ощущение поиска и радости. В случае моей дочери все закончилось хорошо, поскольку в шестом классе она перешла в школу, где не ставили оценок, и снова начала проявлять интерес к учебе. Однако со многими другими этого не происходит, и они проходят программу средней школы, получая все больше оценок и чувствуя себя все менее мотивированными концепциями, которые они изучают.

В моей книге «При чем тут математика?» подробнее рассматривается тема вреда, который наносят оценки и тестирование ученикам всех уровней, а результаты исследований подтверждают негативное влияние такого подхода (Boaler, 2015a). Рекомендую также прочесть очень интересные статьи и книги Элфи Кона о влиянии традиционных методов оценки (Kohn, 1999, 2000). Ниже я сфокусируюсь на способах оценки учеников с ориентацией на рост, предоставляя им информацию и подавая сигналы о мышлении роста, которые помогут им встать на осознанный и позитивный путь к успеху. Это одно из самых важных изменений, которые учитель может предпринять на своих уроках.

Оценка для обучения

Несколько лет назад два профессора из Англии, Пол Блэк и Дилан Уильям, провели метаанализ результатов сотен научных исследований по теме оценки учеников. Они обнаружили нечто поразительное: настолько эффективную форму оценки, что, если бы все учителя начали применять ее, это повысило бы в стране успеваемость, измеряемую в ходе международных исследований, со среднего уровня до одного из первых пяти мест в рейтинге. (Сэр Пол Блэк и профессор Дилан Уильям были моими коллегами в Лондонском университете; Пол Блэк был также моим научным руководителем и наставником.) Блэк и Уильям установили: если бы учителя применяли метод, получивший название «оценка для обучения», это оказало бы гораздо большее положительное влияние по сравнению с другими инициативами в области образования, такими как сокращение численности учеников в классах (Black, Harrison, Lee, Marshall, & Wiliam, 2002; Black & Wiliam, 1998a, 1998b). Блэк и Уильям опубликовали свои выводы в небольшой брошюре, которая разошлась в Англии тиражом 20 тысяч экземпляров за первые несколько недель. Сейчас оценка для обучения получила во многих странах статус инициативы государственного уровня; этот метод опирается на огромную базу результатов научных исследований и доносит до учеников сигналы о мышлении роста.

Думаю, полезно привести здесь вводную информацию по теме. Существует два типа оценки — формативная и суммативная. Первая предоставляет информацию о протекании процесса обучения и представляет собой основу оценки для обучения. Она позволяет выяснить, на каком этапе находятся ученики, чтобы учителя и они сами могли определить, что им изучать далее. А цель суммативной оценки заключается в том, чтобы подвести итоги — составить заключительное мнение о достижениях учеников на конечном этапе обучения. Однако в США есть одна проблема: многие учителя используют суммативное оценивание в формативном режиме, выставляя итоговый балл или оценку еще в процессе изучения материала. На уроках математики учителя часто используют суммативные тесты раз в неделю, а затем переходят к следующей теме, не дожидаясь результатов. В случае оценки для обучения ученики осведомлены о том, что они уже знают, что им необходимо узнать и как преодолеть разрыв между этими двумя пунктами. Подросткам дают информацию об их способах обучения, ориентированных на данность и на рост, что способствует формированию математического мышления роста.

В период прохождения определенного курса очень важна формативная, а не суммативная оценка знаний учеников. Кроме того, подход оценки для обучения, который можно также считать оценкой для мышления роста, предлагает ряд стратегий и методов.

Один из важных принципов оценки для обучения состоит в том, что такой подход возлагает на учеников ответственность за их обучение. По сути, оценка для обучения сводится к предоставлению учащимся возможности стать самостоятельными, самим регулировать учебный процесс и определять, что им необходимо изучить в первую очередь, а также знать, как улучшить свои показатели. Оценку для обучения можно рассматривать как процесс, состоящий из трех частей: предоставление детям четкой информации о том, что они изучили; помощь ученикам в осознании того, где они сейчас и где должны быть; информирование учеников о способах преодоления разрыва между тем, где они есть и где должны быть (рис. 8.1).

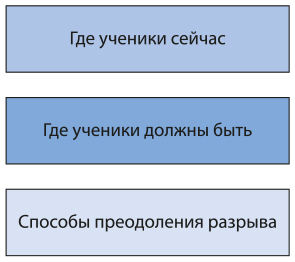
Рис. 8.1. Оценка для обучения

Этот подход обозначается термином оценка для обучения, а не оценка обучения: информация, которую получают учителя и ученики благодаря ему, позволяет учителям сделать свое преподавание более эффективным и помогает ученикам работать с полной отдачей. Учителя, которые используют оценку для обучения, тратят меньше времени на то, чтобы рассказывать ученикам об их успеваемости, и уделяют больше времени созданию возможностей для того, чтобы дети взяли обучение под свой контроль. Учитель из Англии, который начал использовать этот метод, сказал, что это заставило его меньше сосредоточиваться на себе и больше на детях (Black et al., 2002). Он укрепил уверенность в себе как в учителе благодаря эффективным стратегиям создания возможностей для того, чтобы ученики сами продвигали вперед свое обучение.

Развитие самосознания и ответственности учеников

Самые сильные ученики — те, которые склонны к размышлениям, занимаются метапознанием (размышляют о том, что знают) и берут обучение под свой контроль (White & Frederiksen, 1998). У традиционных уроков математики есть один серьезный недостаток: ученики редко знают, что они изучают и где находятся в более широком контексте. Они сосредоточены на методах, которые им необходимо запомнить, но зачастую даже не знают, над какой областью работают. Я неоднократно присутствовала на уроках математики и часто останавливалась возле парт учеников, чтобы спросить их, над чем они работают. Часто ученики просто называют задание. Многие из моих диалогов с ними выглядели примерно так.

Дж. Б.: Над чем вы работаете?

Ученик: Над упражнением 2.

Дж. Б.: Так что же вы делаете на самом деле? Какой материал изучаете?

Ученик: Ой, извините, это вопрос 4.

Научное исследование, которое провели Барбара Уайт и Джон Фредериксен (White & Frederiksen, 1998), убедительно продемонстрировало важность размышлений. Эти исследователи изучили учеников 12 седьмых классов, изучающих физику. Они разделили учеников на экспериментальные и контрольные группы. Все изучали тему «Сила и движение». Ученики контрольных групп уделяли часть каждого урока обсуждению этой работы, а ученики экспериментальных групп на уроках занимались самооценкой и взаимным оцениванием в соответствии с критериями той дисциплины, которую изучали. Результаты исследования оказались весьма неожиданными. Ученики, у которых раньше была низкая успеваемость, добились самых больших успехов. Уделив какое-то время анализу профильных критериев и оценке своей работы в соответствии с ними, они начали добиваться таких же результатов, что и ученики с высоким уровнем успеваемости. Ученики средних классов получили даже более высокие результаты тестирования по курсу физики старшей школы, чем ученики, которые прошли углубленный курс физики. Исследователи пришли к выводу, что низкая успеваемость объясняется скорее не отсутствием у учеников соответствующих способностей, а тем, что раньше они просто не знали, на что им обращать внимание.

К сожалению, это касается многих. Крайне важно довести до сведения учеников, что именно им следует изучать. С одной стороны, это помогает им понять, что такое успех, а с другой — запускает процесс самоанализа, который оказывается бесценным инструментом обучения.

1. Самооценка

Самооценка и взаимная оценка — две основные стратегии, позволяющие ученикам повысить свою осведомленность о том, какую тему они изучают, а также о более широких путях ее исследования. В случае самооценки ученикам дают четкие утверждения по теме, которые они используют для размышлений о том, что они уже изучили и над чем им еще нужно поработать. Такие утверждения должны иметь математическое содержание, например: «Я понимаю разницу между средним и медианным значением и когда каждое из них следует использовать», а также описывать методы работы, например: «Я научился проявлять настойчивость в решении задач и продолжаю работать, даже если задачи трудные». Если ученики начинают каждый раздел работы с четких утверждений об изучаемой теме, они фокусируются на более широком контексте: узнают, что важно, над чем нужно поработать, чтобы улучшить свои знания. Исследования свидетельствуют: когда ученикам предлагают оценить свой уровень понимания, они не завышают и не занижают его (Black et al., 2002).

Самооценку можно проводить на разных уровнях детализации. Учителя могут использовать в листах самооценки критерии, охватывающие урок или более длительный период, например учебный модуль, четверть и полугодие. Ниже приведены примеры критериев самооценки за более короткий и более длинный промежутки. Помимо них, ученикам необходимо предоставить время для размышлений о своем обучении, что они могут сделать во время урока, в конце урока или даже дома.

Лист самооценки из примера 8.1 предоставлен Лори Мэллет, замечательной учительницей третьего класса, с которой я работала. Лори принимала участие в летнем семинаре по профессиональному развитию, который я проводила и на котором мы рассматривали все способы стимулирования мышления роста. Она предлагает ученикам три варианта выбора.

ПРИМЕР 8.1. САМООЦЕНКА: МНОГОУГОЛЬНИКИ

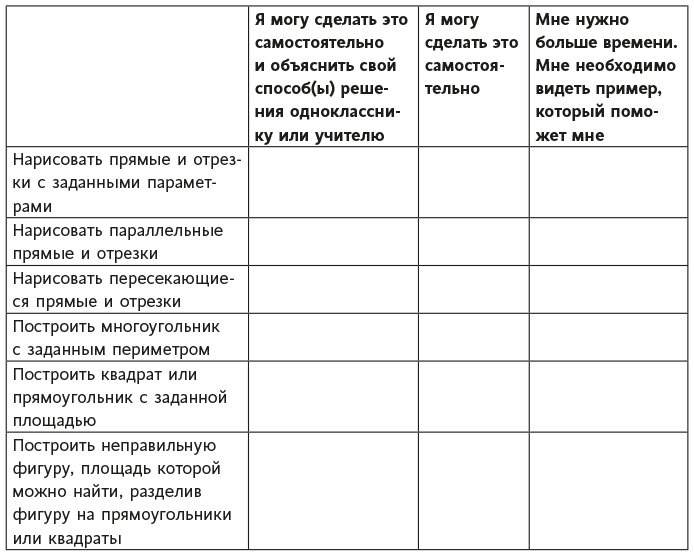
Вместо утверждений, над которыми должны размышлять ученики, некоторые учителя (особенно те, которые учат детей младшего возраста) используют смайлики вроде тех, которые показаны на рис. 8.2.

Рис. 8.2. Смайлики для самоанализа

Оба варианта побуждают учеников подумать о том, что они уже изучили и что им нужно изучить.

Второй пример предоставила Лиза Хенри, опытный учитель старшей школы из Брукленда. Лиза преподает математику в старших классах уже 23 года. Четыре года назад она разочаровалась в системе оценок. Она знала, что ее оценки не отражают реальный уровень знаний учеников. Лиза перешла к оценке знаний по критериям, о которых она рассказала ученикам. Лиза любезно делится со всеми желающими теми утверждениями для самооценки, которые она составила для всего курса алгебры (пример 8.2). Ученики оценивают себя по этим критериям, а Лиза определяет, что они знают, а что нет, вместо того чтобы выставлять общую оценку. Лиза говорит, что теперь ей известно гораздо больше о знаниях и понимании учеников.

ПРИМЕР 8.2. АЛГЕБРА 1. САМООЦЕНКА

Раздел 1 — линейные уравнения и неравенства

• Я могу решить линейное уравнение с одной переменной.

• Я могу решить линейное неравенство с одной переменной.

• Я могу найти формулы для указанной переменной.

• Я могу решить уравнение с модулем с одной переменной.

• Я могу решить составное неравенство с одной переменной и представить его графическое решение.

• Я могу решить неравенство с модулем с одной переменной.

Раздел 2 — интерпретация взаимосвязей в математических выражениях

• Я могу использовать и интерпретировать те или иные компоненты математических формул.

• Я могу преобразовывать компоненты формул.

• Я могу определить, что собой представляет любая часть математического выражения.

• Я могу составить уравнение или неравенство с одной переменной, которое лучше всего описывает задачу.

• Я могу составить уравнение с двумя переменными, которое лучше всего описывает задачу.

• Я могу определить те значения, которые удовлетворяют уравнению, и обосновать свой выбор.

• Я могу использовать полученное решение в описываемой реальной задаче и обосновать свой выбор.

• Я могу построить график уравнения в системе координат с нужными обозначениями и в нужном масштабе.

• Я могу доказать, что любая точка на графике удовлетворяет уравнению, если в него подставить ее координаты.

• Я могу сравнить свойства двух функций, заданных графически, таблично или аналитически.

Раздел 3 — понимание функций

• Я могу определить, представляет ли функцию график, таблица или набор упорядоченных пар.

• Я могу расшифровать запись функции и объяснить, как аргумент согласуется с ее значением.

• Я могу преобразовать список чисел (последовательность) в функцию, сделав целые числа аргументами, а элементы последовательности — значениями функции.

• Я могу выявить основные свойства графика: отрезки, отсекаемые на координатных осях, возрастание или убывание функции, максимальное и минимальное значения и поведение функции на границах области определения, с помощью графика, таблицы или уравнения.

• Я могу объяснить, как график отображает область значений функции.

Раздел 4 — линейные функции

• Я могу вычислить и интерпретировать среднюю скорость изменения функции.

• Я могу построить график линейной функции и определить отрезки, отсекаемые на координатных осях.

• Я могу построить график линейного уравнения на координатной плоскости.

• Я могу продемонстрировать, что линейная функция имеет постоянную скорость изменения.

• Я могу найти ситуации, которые отображают одинаковую скорость изменения за равные промежутки и могут быть смоделированы с помощью линейных функций.

• Я могу построить линейную функцию на основе арифметической последовательности, графика, таблицы значений или описания соотношения.

• Я могу объяснить (с использованием подходящих единиц) значение таких понятий, как угол наклона прямой, отрезок, отсекаемый на оси y, а также другие точки на прямой, когда она моделирует реальное соотношение.

Раздел 5 — системы линейных уравнений и неравенств

• Я могу решить систему линейных уравнений графически.

• Я могу решить систему линейных уравнений методом подстановки.

• Я могу решить систему линейных уравнений методом исключения неизвестных.

• Я могу решить систему линейных неравенств графически.

• Я могу составить и представить в графическом виде набор ограничений для задачи линейного программирования и найти максимальное и (или) минимальное значение.

Раздел 6 — статистические модели

• Я могу описать центр распределения данных (среднее значение или медиану).

• Я могу описать разброс данных (межквартильный диапазон или среднеквадратичное отклонение).

• Я могу представить данные в виде диаграмм с числовой осью (точечных диаграмм, гистограмм и диаграмм размаха).

• Я могу сравнить распределение двух или более множеств данных, проанализировав их форму, центр и разброс, когда они нанесены на одну и ту же шкалу.

• Я могу интерпретировать особенности формы, центра и разброса множества данных в контексте задачи, а также объяснить влияние экстремумов.

• Я могу прочесть и интерпретировать данные, представленные в двумерной таблице плотности распределения.

• Я могу интерпретировать и объяснить значения относительной частоты событий в контексте задачи.

• Я могу построить диаграмму разброса данных, нарисовать линию наилучшего приближения и составить уравнение этой линии.

• Я могу использовать функцию наилучшего приближения для составления прогнозов.

• Я могу проанализировать график остатков, чтобы определить, обеспечивает ли функция приемлемое приближение.

• Я могу вычислить (с помощью разных методов) и интерпретировать коэффициент корреляции.

• Я могу определить, что корреляция не подразумевает наличия причинно-следственной связи и что причинно-следственная связь не отражена на диаграмме разброса.

Раздел 7 — многочлены и функции

• Я могу складывать и вычитать многочлены.

• Я могу умножать многочлен на многочлен.

• Я могу разложить многочлен на множители.

• Я могу решать квадратные уравнения методом разложения на множители.

• Я могу построить приближенный график с помощью точек пересечения квадратичной функции с осями координат и других легко определяемых точек.

Раздел 8 — квадратичные функции

• Я могу найти координаты экстремума квадратичной функции, дополнив ее выражение до полного квадрата.

• Я могу построить график квадратичной функции, определив основные характеристики: отрезки, отсекаемые на координатных осях, максимальное и (или) минимальное значение, симметрия и поведение графика функции на границах области определения.

• Я могу определить, как влияет на график функции то или иное преобразование ее формулы.

• Я могу построить диаграмму рассеяния, используя метод наименьших квадратов, и применить его для составления прогнозов.

Раздел 9 — квадратные уравнения

• Я могу объяснить, почему суммы и произведения либо рациональные, либо иррациональные.

• Я могу решать квадратные уравнения методом дополнения до полного квадрата.

• Я могу решать квадратные уравнения методом нахождения квадратных корней.

• Я могу решать квадратные уравнения с помощью формулы определения корней квадратного уравнения.

Раздел 10 — нелинейные соотношения

• Я могу применить свойства степенных функций, чтобы упростить алгебраические выражения с рациональными показателями степени.

• Я могу построить график степенной функции с показателем степени ¹/₂ или ¹/₃, определив ее основные характеристики: отрезки, отсекаемые на координатных осях, максимальное и (или) минимальное значения и поведение графика функции на границах области определения.

• Я могу построить график кусочно-ломаной функции, в том числе ступенчатой и функции модуля, определив ее основные характеристики: отрезки, отсекаемые на координатных осях, максимальное и (или) минимальное значения и поведение графика функции на границах области определения.

Раздел 11 — показательные функции и уравнения

• Я могу показать, что показательная функция имеет один и тот же множитель при равных интервалах изменения переменной.

• Я могу указать случаи, когда изменение скорости описывается одним и тем же множителем за равные промежутки времени и которые могут быть описаны с помощью показательных функций.

• Я могу использовать графики или таблицы, чтобы сравнить скорость изменения линейной, квадратичной и показательной функций.

• Я могу преобразовать показательную функцию, используя ее свойства.

• Я могу использовать параметры показательной функции, взятые из реальной жизни.

• Я могу построить график показательной функции, определив ее основные характеристики: отрезки, отсекаемые на координатных осях, максимальное и (или) минимальное значения, асимптоты и поведение функции на границах области ее определения.

• Я могу построить диаграмму рассеяния, используя показательную функцию в методе наилучшего приближения, и применить ее для составления прогнозов.

Источник: предоставлено Лизой Хенри.

2. Взаимооценивание

Взаимооценивание — это стратегия, аналогичная самооценке, которая также подразумевает предоставление ученикам четких критериев, но для оценки работы друг друга, а не своей. Оценивая работу знакомого, ученики получают дополнительную возможность для осмысления материала по математике, который им необходимо изучить. Как показала практика, взаимооценивание оказалось весьма эффективным, отчасти потому, что ученики часто гораздо больше открыты для критических замечаний или предложений о внесении изменений от других учеников; кроме того, ровесники обычно используют способ коммуникации, благодаря которому им легче понимать друг друга.

Один из моих любимых методов взаимооценивания — «две звезды и пожелание» (пример 8.3). Ученикам предлагают проанализировать работу одноклассников и с помощью определенных критериев или без них выбрать два фрагмента этой работы, выполненные хорошо, и один, который необходимо улучшить.

ПРИМЕР 8.3. ДВЕ ЗВЕЗДЫ И ПОЖЕЛАНИЕ

Когда ученикам предоставляют информацию, которая позволяет им составить четкое представление о том, что они изучают, и когда им с небольшими интервалами предлагают поразмышлять над своими результатами, у них формируется ответственность за свое обучение. Некоторые называют это приглашением в круг посвященных — предоставлением ученикам мощного знания (которым обычно обладают только учителя), которое позволяет им нести ответственность за свое обучение и добиваться успеха.

3. Время для размышлений

Один из эффективных способов повышения осведомленности учеников об изучаемых концепциях состоит в том, чтобы предоставить им время для размышлений во время занятий. В конце урока предложите им поразмышлять, воспользовавшись такими вопросами, как в примере 8.4.

ПРИМЕР 8.4. РАЗМЫШЛЕНИЯ

Интересная концепция

Над какой интересной концепцией мы работали сегодня?

Что я узнал сегодня?

Какие хорошие идеи появились у меня сегодня?

В каких ситуациях я мог бы использовать полученные сегодня знания?

Какие вопросы у меня есть по поводу сегодняшней работы?

Какие новые идеи появились у меня под влиянием этого урока?

4. Светофор

Этот вид работы в классе стимулирует учеников к размышлениям и дает учителям важную информацию. Есть много разных ее вариантов, но все они подразумевают, что ученики должны использовать красный, желтый и зеленый цвета, чтобы обозначить, понимают ли они тот или иной материал полностью, частично или им необходимо больше поработать над ним. Некоторые учителя раздают цветные бумажные стаканчики: их ученики ставят на парты во время урока. Ученики, которым необходимо, чтобы учитель остановился возле них и просмотрел их работу, ставят на стол красный стаканчик; те, кто считает, что урок проходит слишком быстро, используют желтый. Учителя могут предложить и другие варианты. Сперва некоторые ученики неохотно выставляли стаканчики, но когда поняли, какую пользу это им приносит, начали охотно использовать их. Некоторые учителя предлагают ученикам, на столах которых стоят зеленые стаканчики, объяснить изучаемую концепцию остальным. Это приносит огромную пользу как ученикам, так и учителям: учителя получают обратную связь о своем преподавании в реальном времени, а не в конце модуля или фрагмента работы, когда уже слишком поздно что-то предпринимать. Вместо бумажных стаканчиков можно использовать ламинированные кусочки цветной бумаги, пробив в них отверстия, чтобы их можно было повесить на кольцо.

5. Мозаичные группы

В мозаичных группах ученики работают вместе, чтобы стать экспертами по определенному явлению, новому методу или интересному материалу. Затем группы делятся на части и формируются новые группы, чтобы участники каждой были экспертами в определенной области. После этого члены группы могут обучить друг друга тому, что узнали сами, работая в качестве экспертов. Здесь необходимы минимум четыре области экспертных знаний, чтобы, когда члены группы перейдут в другие группы, все они могли научить друг друга чему-то новому. Класс из 32 учеников, разделенных на восемь групп, может работать так, как показано на рис. 8.3.

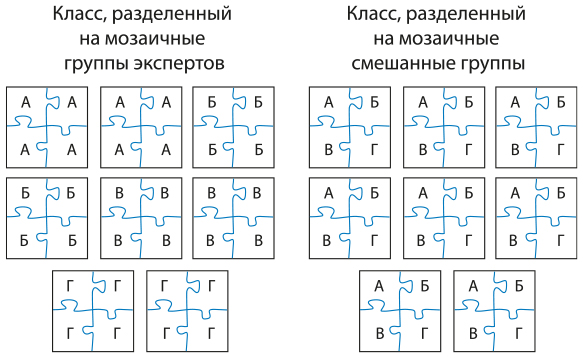
Рис. 8.3. Мозаичные группы

В главе 6 я предложила мозаичное занятие, в ходе которого ученики стали экспертами по вдохновляющим примерам, призванным искоренить стереотипы о том, кто может добиться больших успехов в математике.

Еще одно мозаичное занятие стимулирует учеников к осмыслению существующих в алгебре связей между графиками, таблицами значений, членами уравнения и закономерностями. Учитель раздает ученикам листы с четырьмя закономерностями, такие как в примерах 8.5–8.8, и предлагает группам учеников сделать плакат, иллюстрирующий, как они представляют себе рост фигур, и показывающий таблицу значений, график уравнения, а также закономерность, обобщенную и смоделированную с помощью уравнения. Каждый член группы становится экспертом по нескольким формам представления закономерности. Затем учитель вызывает по одному участнику из каждой группы. Все делятся знаниями о своей задаче с другими членами группы.

ПРИМЕР 8.5. МОЗАИЧНАЯ ЗАДАЧА А ПО АЛГЕБРЕ

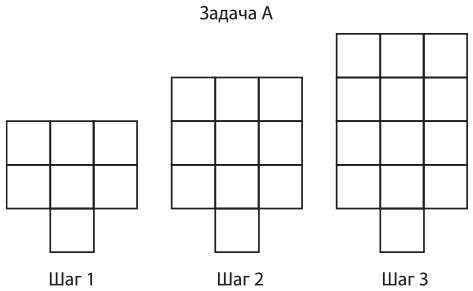
ПРИМЕР 8.6. МОЗАИЧНАЯ ЗАДАЧА Б ПО АЛГЕБРЕ

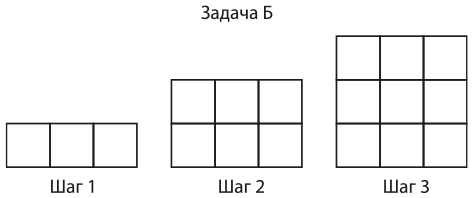
ПРИМЕР 8.7. МОЗАИЧНАЯ ЗАДАЧА В ПО АЛГЕБРЕ

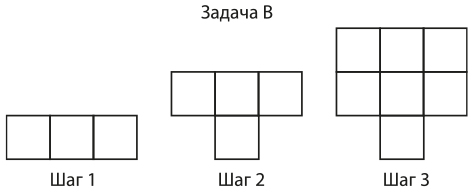
ПРИМЕР 8.8. МОЗАИЧНАЯ ЗАДАЧА Г ПО АЛГЕБРЕ

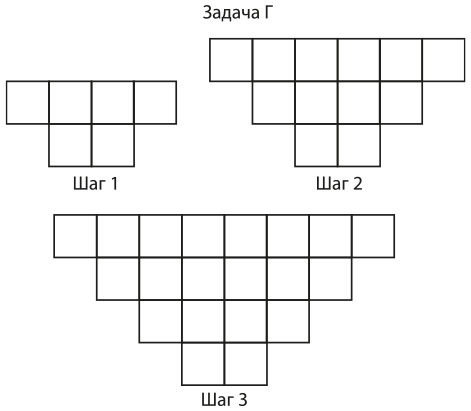
Затем группы обсуждают сходства и различия между разными формами представления своих алгебраических закономерностей.

Когда ученики становятся экспертами и несут ответственность за обучение других, это стимулирует их взять на себя ответственность за новые знания, которые они получают.

6. Билет на выход

Билет на выход — лист бумаги, который вы выдаете ученикам в конце урока и в котором предлагаете рассказать о своем обучении (пример 8.9). Прежде чем уйти из класса, ученики заполняют эти листы и сдают их. Они могут поразмышлять, что способствует их обучению и дает учителям ценную информацию об обучении и идеи для следующего урока.

ПРИМЕР 8.9. БИЛЕТ НА ВЫХОД

Билет на выход _____ Имя _____ Дата _____

Талон на выход _____ Имя _____ Дата _____

7. Онлайн-формы

Я видела, как учителя используют эффективную стратегию, состоящую в том, чтобы предложить ученикам заполнить онлайн-форму в режиме реального времени за время урока и отправить ее на адрес учителя. Можно попросить учеников поделиться комментариями или мыслями по поводу урока. Ученики, которые обычно не принимают активного участия в устном обсуждении, более охотно поделятся своими мыслями в онлайн-режиме. Существует много разных способов использования этой стратегии; в частности, можно попросить учеников прислать свои размышления, предложить проголосовать по какому-то вопросу или показать учителю красный, желтый или зеленый индикатор, который не увидят другие ученики.

8. Рисование в свободной форме

Как было отмечено в главе 4, наука о головном мозге говорит нам, что процесс обучения протекает наиболее эффективно, когда мы используем разные пути в мозге. Этот вывод имеет огромные последствия, которые выходят далеко за рамки методов оценки.

Изучение математики, особенно формальной и абстрактной, на которую приходится большая часть школьной программы, становится эффективнее, когда ученики используют визуальное и интуитивное математическое мышление в сочетании с числовым. Поистине эффективный способ стимулировать учеников к этому сводится к тому, чтобы предложить им нарисовать свои идеи (рис. 8.4).

Рис. 8.4. Математический рисунок в свободной форме

Вместо того чтобы предлагать ученикам записать, что они понимают, во время размышлений на уроке или после урока, попросите их изобразить свое понимание в виде эскиза или комикса. Если вы хотите увидеть и даже показать своим ученикам очень интересные и забавные рисунки о математических концепциях, рекомендую некоторые видео Вай Харт, которые можно найти по следующим адресам.

Спирали, последовательность Фибоначчи — представьте себе, что вы растение (часть 1): https://www.youtube.com/watch?v=ahXIMUkSXX0&list=PLF7CBA45AEBAD18B8&index=8.

Вечеринка треугольников: https://www.youtube.com/watch?v=o6KlpIWhbcw&list=PLF7CBA45AEBAD18B8&index=7.

9. Ученики сами пишут вопросы и тесты

Предложите ученикам написать свои вопросы или критерии оценки для других. Само формулирование правильного вопроса поможет сфокусироваться на том, что важно, и позволит мыслить творчески, что уже важно. Ученики получают истинное удовольствие, когда им дают задание написать утверждения для оценки работы по математике.

Комментарии

Все представленные выше стратегии позволяют достичь целей первых двух частей трехэтапного процесса оценки для обучения: эти стратегии помогают ученикам понять, что они изучают и что должны изучить.

Части 1 и 2 процесса оценки для обучения играют очень важную роль сами по себе, а часть 3 дает ученикам поддержку, которую не может предоставить никакой другой метод. Это крайне важная часть процесса оценки для обучения, позволяющая ученикам понять, как преодолеть разрыв между тем, где они есть, и тем, где должны быть. В этой области есть один метод, который превосходит остальные по своей эффективности: процесс, в ходе которого учителя дают ученикам комментарии по поводу их работы. Величайший дар, который вы можете передать своим ученикам, — ваши знания, идеи и обратная связь об их математическом развитии, наряду с позитивными высказываниями и сигналами по поводу мышления роста.

Эллен Круз — одна из тех учителей, с которыми я работала в школьном округе Виста. Во время наших занятий по профессиональному развитию я поделилась с Эллен и другими учителями результатами исследований, о которых шла речь выше, продемонстрировав им положительное влияние комментариев в качестве альтернативы оценкам. Эллен — удивительная и преданная делу учительница, которая работает в непростой школе, находящейся на этапе «улучшения программы». Ведь штат Калифорния отнес эту школу к числу работающих недостаточно эффективно. В ней разнородный состав учеников: 90% — латиноамериканцы, а оставшиеся 10% приходятся на другие этнические группы. 43% учеников изучают английский язык и 86% имеют право на бесплатные обеды. Эллен рассказала мне, что, когда она начала преподавать в этой школе, руководство было сфокусировано на тестировании, что типично для школ, получивших ярлык «улучшенная программа». Вопросы тестов и тесты по учебным разделам в точности воспроизводили вопросы стандартного с несколькими вариантами ответов. Школа была сосредоточена на «улучшении» (звучит неплохо), и учителя часами сидели над отчетами, сгенерированными программами для проведения тестов, отслеживая закономерности. Затем каждому ученику присваивали определенный цвет, а учителям говорили, что «синие» успешно справятся с тестом штата, а у «красных» почти нет шансов. Учителям говорили, что они должны сосредоточиться на нижнем сегменте «зеленых» учеников и на верхнем сегменте «желтых», поскольку повышение их успеваемости окажет самое большое влияние на результаты тестирования.

Попытки «улучшения» заслуживают похвалы, но метод, который применила эта школа (что типично для школ, проходящих процедуру улучшения программы), выдвигал на первый план группы учеников, способных повысить результаты тестирования, а не делал упор на потребностях конкретных учеников. Школа сначала распределила детей по результатам тестов, а затем и по цветам, от которых зависело, кто получит меньше внимания (ими оказались ученики как с высокой, так и с низкой успеваемостью). Такой подход, подразумевавший работу с детьми как со статистическими показателями, которыми можно манипулировать, используется везде в США, как правило, в ответ на жесткие суждения и ярлыки, навешиваемые во имя «улучшения».

В разгар внедрения культуры достижений, навязанной этой школе, Эллен решила провести среди учеников опрос. Как и следовало ожидать, она обнаружила высокий уровень тревоги в связи с тестами. Ученики сдавали многочисленные тесты, а учителям дали указание постоянно подчеркивать важность эффективной работы в условиях стресса. Эллен хотела изменить эту культуру и для начала отменила тесты по разделам и заменила их оценкой более мелких учебных модулей. Эллен прекратила использовать слова «тест» и «проверка» и назвала свои мини-экзамены возможностью «показать, что вы знаете». Вопросы с несколькими вариантами были исключены, ученикам предлагали ответить на математические вопросы. Кроме того, Эллен прекратила готовить учеников к эталонным экзаменам на уровне школьного округа; она проводила такие экзамены без предупреждения, чтобы предотвратить усиление тревоги, советуя ученикам: «Сделайте всё возможное и ни о чем не беспокойтесь». Результаты тестов не ухудшились, несмотря на отсутствие предварительной подготовки и сосредоточения на тестах, а уровень тревожности учеников снизился. Важно то, что, как сказала мне Эллен, дети начали получать удовольствие от уроков математики.

Но Эллен (как и другие думающие, неравнодушные учителя) не остановилась на этом, а предприняла следующие шаги для улучшения ситуации. В следующем году Эллен и ее коллеги — преподаватели математики в восьмом классе, Аннет Уилсон и Анджела Тайнсенд, — перестали ставить ученикам оценки, а использовали листы с математическими утверждениями. Кроме того, все учителя этой группы изменили названия своих систем оценки на такое: «Покажите, что вы можете сделать» (пример 8.10).

ПРИМЕР 8.10. САМООЦЕНКА «ПОКАЖИТЕ, ЧТО ВЫ МОЖЕТЕ СДЕЛАТЬ»

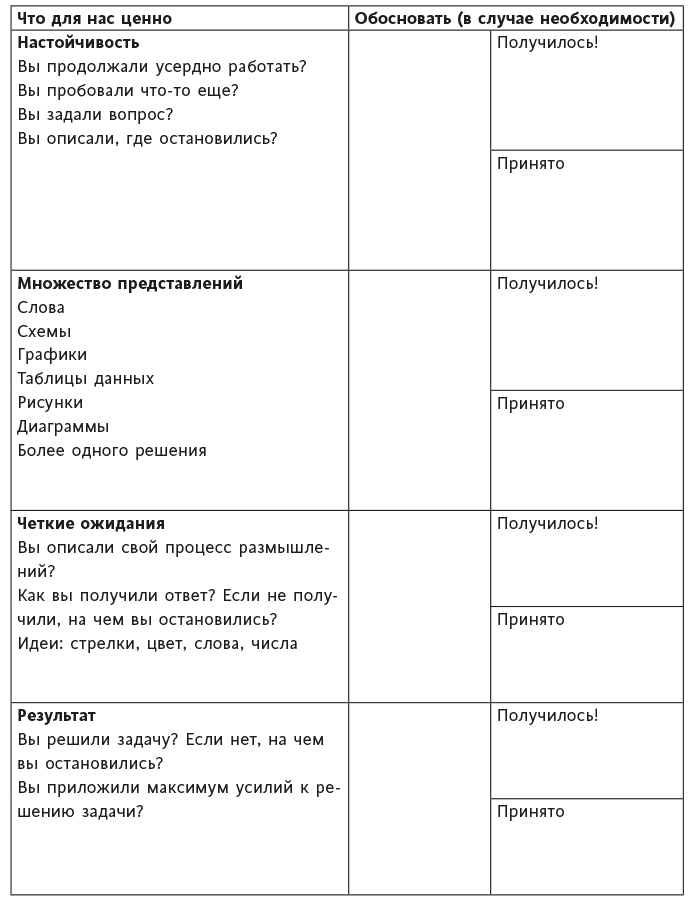
Источник: предоставлено Эллен Круз.

Когда эта группа учителей прекратила ставить оценки, используя вместо них комментарии, ученики начали читать и интерпретировать эту обратную связь и время от времени задавать вопросы. Эллен ставила оценки только тогда, когда ученики просили ее об этом. Она сказала мне, что поначалу ей приходилось тратить слишком много времени на обратную связь, которую она регулярно предоставляла всем своим 110 ученикам, и она научилась писать комментарии тогда, когда это приносило максимальную пользу ученикам. Это идеальный подход к обратной связи. Он отнимает не больше времени, чем проверка заданий или выставление оценок, но приносит гораздо больше пользы ученикам. Периодическая обратная связь, предоставляемая в профессионально рассчитанные важные моменты, — бесценный дар, но его не следует применять слишком часто.

Эллен рассказала мне, что сейчас гораздо больше учеников старательно занимаются математикой и она видит, как они стремятся работать с полной отдачей. Идеальный результат. Эллен рассказала также об усовершенствованиях в ее методах преподавания, проистекающих из полезной информации, которая получена благодаря новым формам оценки и которую она использует для планирования обучения. За годы, прошедшие после того, как Эллен внесла изменения в свой подход к преподаванию и оценке, отметки учеников, которые переходят в старшие классы, существенно улучшились, а количество неудач с изучением алгебры в старшей школе сократилось вдвое.

Рекомендации по выставлению оценок

К сожалению, многие учителя вынуждены ставить оценки, поскольку того требует школьный округ или руководство школы. Теоретически они должны ставить оценки только в конце курса, а не во время его прохождения, когда школьникам нужна информация о том, как учиться лучше, которую необходимо предоставлять в рамках формативного оценивания. Ниже представлен список рекомендаций, как справедливо ставить оценки и при этом подавать ученикам позитивные сигналы о мышлении роста.

1. Всегда давайте ученикам возможность повторно представить любую работу или сдать тест, чтобы получить более высокую оценку. Это сильнейший сигнал о мышлении роста, который говорит ученикам, что вас заботит обучение, а не одни только результаты. Некоторые учителя говорят мне, что это несправедливо: ученики могут самостоятельно изучить то, что им необходимо, чтобы улучшить свою оценку. Но мы должны ценить такие усилия, ведь они направлены на обучение.

2. Сообщайте об оценках руководству школы, а не ученикам. Если в вашей школе надо ставить оценки до завершения курса, не обязательно сообщать о них ученикам. Предоставьте им вербальную или диагностическую обратную связь о способах улучшения результатов.

3. Используйте многоплановую систему выставления оценок. Учителя могут считать математику обширной дисциплиной и ценить многоплановый подход к ее изучению на уроках, но при этом оценивать работу учеников только по тому, дают ли они правильные ответы на процедурные вопросы. Лучшие учителя, с которыми я работала и которые ставили оценки, рассматривали скорее работу учеников, а не результаты тестов — записывая, например, задают ли они вопросы, представляют задачи разными способами, рассуждают и обосновывают свой выбор и опираются на размышления друг друга. Иными словами, такие учителя оценивают многоплановость математики. В случае оценки разных способов выполнения работы гораздо больше учеников успешно справляются с заданиями.

4. Не применяйте 100-балльную шкалу. Один из самых несправедливых и бессмысленных с математической точки зрения методов выставления оценок — когда учителя используют несколько заданий в качестве основы для оценки, исходя из того, что каждое из них оценивается в 100 баллов, и присваивая 0 баллов за любое незаконченное, отсутствующее или неправильно выполненное задание. Дуглас Ривз (Reeves, 2006) доказал, что такая практика противоречит логике: разрыв между оценками A, B, C и D составляет 10%, а между D и F — 60%. Следовательно, отсутствие какого-либо задания может означать, что ученик получит вместо оценки A оценку D. Ривз рекомендует использовать четырехбалльную шкалу (A = 4, B = 3, C = 2, D = 1, F = 0), в которой все интервалы равны, вместо шкалы, которая не имеет смысла с математической точки зрения:

A = 91+

B = 81–90

C = 71–80

D = 61–70

F = 0

5. Не включайте задания, выполненные в начале урока, в оценку, которая выставляется в конце урока. Когда учителя делают это, они, по сути, ставят ученикам оценку за работу на предыдущем уроке. Но ведь оценки должны отражать то, что ученики освоили на текущем уроке.

6. Не включайте домашние задания (если они есть) в систему оценки. Как сказано в главе 6, домашние задания — одна из самых несправедливых практик в сфере образования. Их включение в систему оценок повышает уровень стресса учеников, а также вероятность несправедливых результатов.

Резюме

Когда учителя оценивают работу учеников, у них появляется замечательная возможность: дать школьникам информацию об их обучении (а не успеваемости), что ускоряет путь к успеху и подает сильные сигналы в отношении мышления роста в связи с математикой и обучением. Есть немало результатов научных исследований, свидетельствующих, что переход от выставления отметок и тестирования к методам оценки для обучения оказывает огромное положительное влияние на успеваемость, уверенность в себе, мотивацию и будущее учеников. В данной главе идет речь о работе преданных делу и вдумчивых учителей, которые совершили такой переход. В заключительной главе приведен краткий обзор разных способов проведения уроков математики, ориентированных на мышление роста.