Задачи и упражнения.

1. Любая матрица является прямоугольной таблицей. Справедливо ли обратное утверждение, т.е. можно ли считать всякую прямоугольную таблицу матрицей? Если нет,то какие дополнительные требования выдвигаются с позиций матричной алгебры?

2. Какие из приведенных ниже совокупностей объектов представляют собой матрицы:

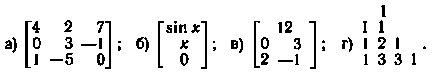
3. Укажите, какие из приведенных ниже матриц являются равными между собой (при x=2)%

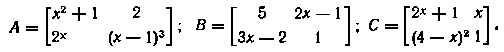
4. При каком значении x матрицы А и В равны:

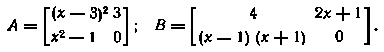
5. Найти сумму А + В и разность А — В матриц:

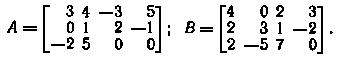
6. Найти произведения АВ и ВА и сравнить полученные результаты для матриц:

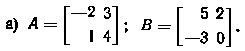
- 42 -

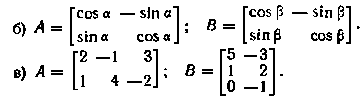
7. Проверить дистрибутивность умножения слева А(В + С) = АВ + АС и справа (А + В)С = АС + ВС относительно сложения для следующих матриц:

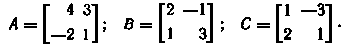
8. Найти все матрицы, перестановочные с матрицей

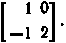
9. Каким условиям в общем случае должны удовлетворять элементы квадратных матиц А и В второго порядка, чтобы они были перестановочными (АВ = ВА)? Как выглядят эти условия для случая, когда А симметричная матрица?

10. При каких условиях справедливы матричные соотношения:

(A + B)² = A² + 2AB +B²; (A-B)(A+B) = A² — B²?

11. Каким условиям должны удовлетворять элементы ненулевых квадратных матриц А и В, чтобы АВ = 0?

12. К каким типам относятся матрицы:

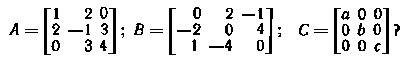
13. Построить транспонированную A^t, комплексно-сопряженную A̅ и сопряженную А* для матрицы

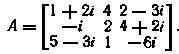
14. Показать, что матрица

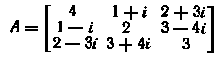
является эрмитовой. Что можно сказать о диагональных элементах любой эрмитовой матрицы?

15. Какого типа должна быть квадратная матрица А, чтобы она была перестановочной с диагональной матрицей D того же порядка, т.е. чтобы AD = DA?

16. К какому типу относятся треугольные матрицы, если они кроме того: а) симметричные, б) кососимметричные?

17. Показать, что (A̅B̅) = A̅ B̅ и (AB)* = B* A*.

18. Проверить соотношение (AB)* = B*A* для матриц задачи 6в.

19. Показать, что произведение AA^t существует для любой матрицы А и является симметричной матрицей.

- 43 -

20. Для заданных матриц найти обратные и проверить соотношение AA^-1 = 1:

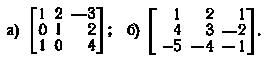
21. Найти матрицы, обратные заданным, и проверить соотношение (AB)^-1 = B^-1A^-1:

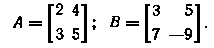
22. Дана система уравнений:

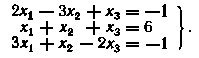
Записать эту систему в матричной форме Ax = q, вычислить обратную матрицу А^-1 и записать решение системы.

23. Зависимости между токами и напряжениями четырехполюсника (рис. 6, а) можно представить одной из систем уравнений:

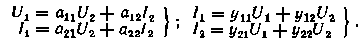
Рис. 6. Соединение четырехполюсника: а — четырехполюсник; б — последовательное соединение; в — параллельное соединение.

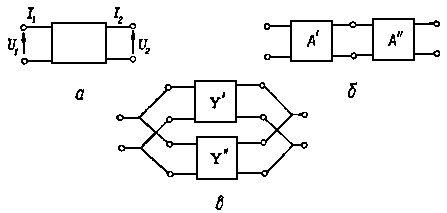
а) Записать эти уравнения в матричной форме и установить зависимости между элементами матриц:

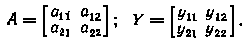
б) Показать, что матрица А последовательного соединения четырехполюсников (рис 6. б) равна произведению их матриц A' и A'', т.е. A = A' A'' (в порядке следования).

в) Показать, что матрица Y параллельного соединения четырехполюсников (рис. 6, в) равна сумме их матриц Y' и Y'', т.е. Y = Y' + Y''.

- 44 -

24. Выполнить умножение матриц, воспользовавшись разбиением их на блоки:

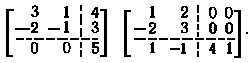
Проверить результат непосредственным умножением матриц.