1. Логические функции

1. Логические функции как отображения. Отличительная особенность логических функций состоит в том, что они принимают значения в конечных множествах. Иначе говоря, область значений логической функции всегда представляет собой конечную совокупность чисел, символов, понятий, свойств и, вообще, любых объектов. Если область значений функции содержит k различных элементов, то она называется k-значной функцией.

Чтобы различать элементы области значений функции, их необходимо как-то отметить. Удобнее всего элементы перенумеровать числами от 1 до k или обозначить какими-нибудь символами (например, буквами). Перечень всех символов, соответствующих области значений, называют алфавитом, а сами символы — буквами этого алфавита (буквами могут служить как собственно буквы латинского, русского или другого алфавита, так и порядковые числа или любые другие символы).

- 504 -

Логические функции могут зависеть от одной, двух и, вообще, любого числа переменных (аргументов) x₁, x₂, ..., x_n. В отличие от самой функции, аргументы могут принимать значения из элементов как конечных, так и бесконечных множеств.

В теоретико-множественном смысле логическая функция n переменных y = f(x₁, x₂, ..., x_n) представляет собой отображение множества наборов (n-мерных векторов, кортежей, последовательностей) вида (x₁, x₂, ..., x_n), являющегося областью ее определения, на множестве ее значений N = {α₁, α₂, ..., α_n}. Логическую функцию можно также рассматривать как операцию, заданную законом композиции X₁, X₂, ..., X_n где - множества, на которых определены аргументы x₁ ∈ X₁, x₂ ∈ X₂, ..., x_n ∈ X_n.

2. Однородные функции. Если аргументы принимают значения из того же множества, что и сама функция, то ее называют однородной функцией. В этом случае X₁ = Х₂ = ... = Х_n = N и однородная функция, рассматриваемая как закон композиции Nⁿ → N определяет некоторую п-местную операцию на конечном множестве N.

Областью определения однородной функции у = f(х₁, х₂, ..., x_n) служит множество наборов (х₁, х₂, ..., x_n), называемых словами, где каждый из аргументов х₁, х₂, ..., x_n замещается буквами k-ичного алфавита {0, 1, ..., k -1}. Количество n букв в данном слове определяет его длину.

Очевидно, число всевозможных слов длины n в k-ичном алфавите равно kⁿ. Так как каждому такому слову имеется возможность предписать одно из k значений множества N, то общее количество однородных функций от n переменных выражается числом k^(kn).

Если буквами алфавита служат числа от 0 до k - 1, то каждое слово (х₁, х₂, ..., x_n) символически представляется упорядоченной последовательностью n таких чисел и рассматривается как запись n-разрядного числа в позиционной системе счисления с основанием k, т. е. x₁k^{n -1} + x₂k^{n –2} + … + x_{n -1}k¹ + x_nk⁰ = q. Числа q = 0, 1, ..., kⁿ - 1 служат номерами слов и тем самым на множестве всех слов вводится естественная упорядоченность (отношение строгого порядка). Аналогично номерами функций можно считать kⁿ -разрядные числа в той же системе счисления.

Различные слова длины n в данном алфавите образуются как n-перестановки с повторениями (2. 10. 1). Так, в трехзначном алфавите {0, 1, 2} словами длины 4 будут все четырехразрядные числа с основанием k = 3, т. е. 0000, 0001, 0002, 0010, 0011, ..., 2221, 2222, которые соответствуют десятичным числам от 0 до 80 = 2 · З³+ 2 · З²+ 2 · З¹ + 2 · 3⁰. Поставив каждому такому четырехразрядному числу в соответствие одну из букв алфавита {0, 1, 2}, получим некоторую функцию четырех переменных

- 505 -

f_i(х₁, х₂, x₃, x₄), причем количество таких функций выражается огромным числом 3⁸¹.

Пусть алфавит состоит из трех букв русского алфавита {о, п, т}. Множество пятибуквенных слов в этом алфавите состоит из 3⁵ = 243 элементов. Наряду с такими имеющими прямой смысл словами, как «топот» и «потоп», оно также включает все другие 5-перестановки, например: «ооппт», «поппп», «тттоп» и др.

Примерами однородных логических функций двух переменных могут служить операции сложения и умножения одноразрядных m-значных чисел по модулю т (2. 8. 7), внутренние операции поля Галуа (2. 8. 9) с четырехзначным алфавитом {0, 1, А, В} и т. п.

3. Табличное задание функций. Как и бинарный закон композиции (2. 7. 2), однородная функция двух переменных может быть задана таблицей соответствия (матрицей), строки и столбцы которой соответствуют буквам алфавита. Таким способом представлялись функции одной и двух переменных в (1. 5. 2),(1. 5. 8) и (1. 5. 10). Для представления функций трех и большего числа переменных потребовались бы трехмерные и, вообще, n-мерные таблицы. Этого можно избежать, если столбцы матрицы поставить в соответствие не буквам алфавита, а словам, т. е. образовать kⁿ столбцов. Для каждой функции отводится строка, клетки которой заполняются буквами из данного алфавита. Матрица всех функций n переменных в k-значном алфавите содержит k^kn строк и называется общей таблицей соответствия. Например, для k = 3 и n = 2 такая матрица имеет вид:

Номера столбцов определяются расположенными над ними n-разрядными числами с основанием k, каждое из которых читается сверху вниз. Номера функций отождествляются с kⁿ-разрядными числами, которые соответствуют строкам матрицы в той же системе счисления.

4. Двузначные однородные функции. Наиболее простым и в то же время важнейшим классом однородных функций являются двузначные (булевы) функции, частично рассмотренные в (1.5. 2) и последующих пунктах.

- 506 -

Областью определения булевых функций от n переменных служит множество слов длины n. Они представляют собой всевозможные наборы из n двоичных цифр и их общее количество равно 2ⁿ.

Число всевозможных булевых функций n переменных v = 2ⁿ быстро возрастает с увеличением n (при n = 3 оно равно 256, а при n = 5 превышает 4 миллиарда). Но функции одной и двух переменных еще можно перечислить и подробно исследовать, так как их количество сравнительно невелико (v = 4 при п = 1 и v = 16 при n = 2).

5. Булевы функции одной переменной. Общая таблица соответствия для булевых функций одной переменной имеет вид (справа указаны обозначения функций):

x

0

1

y₀ = 0

0

0

y₁ = x

0

1

y₂ = x̅

1

0

y₃ = 1

1

1

Две функции у₀ = 0 и у₃ = 1 представляют собой функции-константы (тождественный нуль и тождественная единица), таккакони не изменяют своих значений при изменении аргумента. Функция y₁ = х повторяет значения переменной х и потому просто совпадает с ней.

Единственной нетривиальной функцией является у₂ = x̅ , называемая отрицанием или инверсией ( x̅ читается «не х»). Она равна 1, когда аргумент принимает значение 0, и равна 0 при аргументе 1.

6. Булевы функции двух переменных. Все 16 функций двух переменных приведены в табл. 6, где указаны условные обозначения, названия и чтения функций (в скобках даны встречающиеся в литературе варианты).

Шесть из приведенных функций не зависят от x₁ или x₂ (или от обоих вместе). Это две константы (y₀ = 0 и y₁₅ = 1), повторения (y₃ = х₁ и y₅ = х₂) и отрицания (y₁₀ = x̅₂, и y₁₂ = x̅₁), являющиеся функциями одной переменной (х₁ или x₂). Из остальных десяти функций две (y₄ и y₁₁) отличаются от соответствующих им (y₂ и y₁₃) лишь порядком расположения аргументов и поэтому не являются самостоятельными. Поэтому из 16 булевых функций двух переменных только восемь являются оригинальными (y₁, y₂, y₆, y₇, y₈, y₉, y₁₃, y₁₄).

Рассмотрение булевых функций одной, двух и большего числа переменных показывает, что всякая функция от меньшего числа переменных содержится среди функций большего числа переменных. Функции, которые сводятся к зависимости от меньшего числа переменных, называют вырожденными, а функции, существенно

- 507 -

Таблица 6

Булевые функции двух переменных

x₁ x₂

0011

0101

Обозначения

Названия

Чтение

y₀

0000

Константа 0 (тождественный нуль, всегда ложно)

Любое 0

y₁

0001

x₁x₂; x₁ ∧ x₂ ( x₁ & x₂ ; x₁ ∩ x₂ )

Конъюнкция (совпадение, произведение, пересечение, логическое «и»)

x₁ и x₂ (и x₁ и x₂)

y₂

0010

x₁←x₂

( x₁⊃x₂ ; x₁x₂ )

Отрицание импликации (совпадение с запретом, антисовпадение, запрет)

x₁, но не x₂

y₃

0011

x₁

Повторение (утверждение, доминация) первого аргумента

Как x₁

y₄

0100

x₂⊃x₁ ( x₂ ⊄ x₁ ; x₂ x₁ )

Отрицание обратной импликации (обратное антисовпадение)

Не x₁, но x₂

y₅

0101

x₂

Повторение (утверждение, доминация) второго аргумента

Как x₂

y₆

0110

x₁ + x₂ ( x₂ ⊕ x₁ )

Сумма по модулю 2 (неравнозначность, антиэквивалентность)

x₁ не как x₂ (или x₂ или x₁)

y₇

0111

x₁ ∨ x₂ (x₁ + x₂; x₁ ∪ x₂ )

Дизъюнкция (разделение, логическая сумма, сборка, логическое «или»)

x₁ или x₂ (x₁ или хотя бы x₂)

y₈

1000

x₁ ↓ x₂ ( x₁ ∨̅ x₂ ; x₁ ○ x₂ )

Стрелка Пирса (функция Вебба, отрицание дизъюнкции, логическое «не – или»)

Ни x₁,ни x₂

- 508 -

Продолжение табл. 6

x₁ x₂

0011

0101

Обозначения

Названия

Чтение

y₉

1001

x₁ ~ x₂ ( x₁ ≡ x₂ ; x₁ ↔ x₂)

Эквиваленция (равнозначность, эквивалентность, взаимозависимость)

x₁ как x₂ (x₁, если и только если x₂)

y₁₀

1010

x̅₂ (x'₂; ~x₂; ¬ x₂)

Отрицание (инверсия) второго аргумента (дополнение к первой переменной)

Не x₂

y₁₁

1011

x₂ → x₁ ( x₁ ⊂ x₂ ; x₁ < x₂ )

Обратная импликация (обратное разделение с запретом, обратная селекция)

Если x₂, то x₁ (x₁ или не x₂)

y₁₂

1100

x̅₁ (x₁; ~x₁; ¬ x₁)

Отрицание (инверсия) первого аргумента (дополнение к первой переменной)

Не x₁

y₁₃

1101

x₁→x₂ ( x₁⊃x₂ ; x₁ > x₂ )

Импликация (разделение с запретом, следование, селекция)

Если x₁, то x₁ (не x₁ или x₂)

y₁₄

1110

x₁ / x₂ ( x₁ ∧̅ x₂ ; x₁ &̅ x₂ )

Штрих Шеффера (отрицание конъюнкции, несовместность, логическое «не – и»)

Не x₁ или не x₂

y₁₅

1111

1

Константа 1 (тождественная единица, всегда истино)

Любое 1

зависящиеот всех переменных, являются невырожденными. Так, среди функций одной переменной имеются две вырожденные (константы 0 и 1, которые можно рассматривать как функции от нуля переменных), функции двух переменных содержат те же константы и четыре функции одной переменной и т. д.

7. Зависимость между булевыми функциями.Из табл. 6 видно, что между функциями имеются зависимости y_i = y̅_15-i (i = 0, 1, ... ..., 15), на основании которых можно записать соотношения для констант 0=1̅ и 1=0̅, для функции одной переменной х = x̿ и для функций двух переменных:

x₁x₂ = ¬(x₁ / x₂) ; x₁←x₂ = ¬(x₁ → x₂) ; x₁ + x₂ = ¬(x₁ ~ x₂) ; x₁ ∨ x₂ = ¬(x₁ ↓ x₂) ,

или

x₁/x₂ = ¬(x₁x₂) ; x₁→x₂ = ¬(x₁←x₂) ; x₁ ~ x₂ = ¬(x₁ + x₂) ; x₁ ↓ x₂ = ¬(x₁ ∨ x₂) .

- 509 -

Из этих зависимостей следует, что любая функция двух переменных (включая константы) выражается в аналитической форме через совокупность шести функций, содержащей отрицание x̅ и любую из каждой пары функций {y₀, y₁₅},{y₁, y₁₄},{y₂, y₁₃}, {y₆, y₉}, {y₇, y₈}. Например, такой совокупностью могут служить функции: константа 0, отрицание`х, конъюнкция х₁x₂, дизъюнкция x₁ ∨ x₂ ,эквиваленция х₁ ~ x₂ и импликация x₁→x₂ . Как уже упоминалось в (1. 5. 8), они используются в исчислении высказываний.

Выбранная таким способом совокупность шести функций является избыточной. Можно показать, что импликация и эквиваленция выражаются через остальные функции этой совокупности:

x₁ → x₂ = x̅₁ ∨ x₂

x₁ ~ x₂ = (x₁ ∨ x̅₂)(x̅₁ ∨ x₂).

Для этого достаточно построить таблицу соответствия и сравнить ее с табл. 6:

x₁

0

0

1

1

x₂

0

1

0

1

x̅₁

1

1

0

0

x̅₂

1

0

1

0

(x̅₁ ∨ x₂)

1

1

0

1

x₁→x₂

(x₁ ∨ x̅₂)

1

0

1

1

(x₁ ∨ x̅₂)(x̅₁ ∨ x₂)

1

0

0

1

x₁ ~ x₂

Таким образом, комплект элементарных функций сокращается до четырех: константа 0, отрицание x̅ , конъюнкция x₁x₂ и дизъюнкция x₁ ∨ x₂ . Этот комплект обладает существенными удобствами и часто применяется на практике, но и он может быть сокращен. Так, из законов де Моргана и свойства двойного отрицания вытекают тождества:

x₁ ∨ x₂ = ¬(x̅₁x̅₂); x₁x₂ = ¬(x̅₁ ∨ x̅₂).

Отсюда следует, что булевы функции выражаются через отрицание и конъюнкцию или через отрицание и дизъюнкцию.

Более того, для записи любой булевой функции достаточно только одной из двух элементарных функций — стрелки Пирса или штриха Шеффера. Это вытекает из соотношений (их доказательство приводится аналогично с помощью таблиц соответствия):

x̅ = x ↓ x = x/x;

x₁x₂ = (x₁/x₂)/(x₁/x₂); (x₁ ↓ x₂).

8. Булевы функции многих переменных. С помощью суперпозиции функций, т. е. подстановки в логические формулы вместо переменных некоторых булевых функций, можно получить более сложные

- 510 -

функции от любого числа переменных. Например, подставляя в выражение аb формулы a = x₁ ∨ x₂ и b = x₂ → c, а также c=x̅₃, получаем (x₁ ∨ x₂)(x₂ → x̅₃) . Таблица соответствия для сложных формул записывается на основании общей таблицы для элементарных функций. Для данного примера она имеет вид:

x₁

0 0 0 0 1 1 1 1

x₂

0 0 1 1 0 0 1 1

x₃

0 1 0 1 0 1 0 1

x₁ ∨ x₂

0 0 1 1 1 1 1 1

x̅₃

1 0 1 0 1 0 1 0

x₂ → x̅₃

1 1 1 0 1 1 1 0

(x₁ ∨ x₂)(x₂ → x̅₃)

0 0 1 0 1 1 1 0

Если на всех наборах значений переменных функция принимает значение 0 или 1, то она вырождается в соответствующую константу и называется тождественным нулем или тождественной единицей.

Например, x ∨ x̅ = 1; xx̅ = 0; xx̅ ∨ xx̅y =0; ((xy ∨y̅z → z̅) ∨ (x∨y̅)z = 1; x(x → y) → y = 1 и т. п.

9. Геометрическое представление. Область определения булевых функций от п переменных y = f(х₁, x₂, ...,x_n) можно рассматривать как совокупность n-мерных векторов (слов длины n), компонентами которых являются буквы 0 и 1 двоичного алфавита. При п = 3 каждый вектор представляется вершиной единичного куба в трехмерном пространстве (рис. 188).

В общем случае совокупность векторов (х₁, x₂, ...,x_n) отображается на множество вершин n-мерного куба.Всетакие вершины образуют логическое пространство.

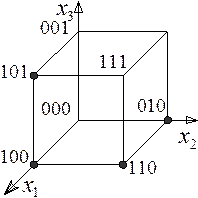
Рис. 188. Отображение булевой функции y = (х₁ ∨ х₂) × (х₂ → х̅₃) на трехмерном кубе.

Булева функция отображается на n-мерном кубе путем выделения вершин, соответствующих векторам (х₁, x₂, ...,x_n) на которых булева функция y = f(х₁, x₂, ...,x_n) принимает значения 1. Обычно такие вершины отмечают жирными точками. Так, на рис. 188 отображена функция (х₁ ∨ х₂)(х₂ → х̅₃) в соответствии с таблицей из (8).

10. Неоднородные функции. Аргументы неоднородных функций в отличие от однородных, могут принимать значения из любых конечных или бесконечных множеств, но область определения значений самих функций ограничена конечными множествами.

- 511 -

Важным примером неоднородных функций являются двузначные n-местные предикаты (1.5.9). Предикат Р (x₁, x₂, ..., x_n) принимает одно из двух значений - «истинно» (1) или «ложно» (0) в зависимости от конкретных значений, приписываемых переменным x₁, x₂, ..., x_n. Если значения переменных выбираются из некоторого множества М (универсума), то n-местный предикат можно рассматривать как n-местное отношение, определенное на этом множестве.

Одноместный предикат P(x) задает некоторое свойство элементов множества М и вполне определяется подмножеством P ⊂ M тех объектов x ∈ M, на которых он принимает значение «истинно».

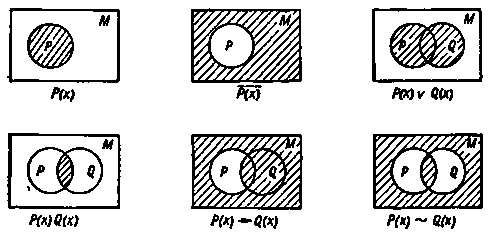
Рис. 189. Характеристические подмножества, соответствующие операциям над предикатами (область истинных значений заштрихована).

Множество объектов, на которых предикат P(x) принимает значение «ложно», соответствует дополнению множества P, т.е. P̅. Очевидно, если P(x) истинно, то P̅(x) — ложно и наоборот. Например, если на множестве натуральных чисел определен предикат P(x) = «x — четное число», то P̅(x) - «x — нечетное число». Таким образом, одноместный предикат, определенный на множестве М разбивает это множество на два подмножества P и P̅. Подмножество P ⊂ M, на котором предикат P(x) принимает значение «истинно», называется характеристическим подмножеством.

Пусть на М определены два предиката P(x) и Q(x), характеристическими подмножествами которых являются соответственно P и Q. Рассматривая предикаты как двузначные функции, можно с помощью операций алгебры логики строит новые одноместные предикаты на множестве М. Конъюнкция P(x) и Q(x) — это предикат R(x) = P(x) ∧ Q(x), который истинен для тех и только тех объектов из М, для которых оба предиката P(x) и Q(x) истинны.

- 512 -

Характеристическим множеством предиката R(x) является пересечение P ∩ Q. Подобным образом вводятся и операции дизъюнкции P(x) ∨ Q(x), импликации P(x) → Q(x), эквиваленции P(x) ~ Q(x) и др. На рис. 189 показаны соответствующие этим операциям характеристические подмножества (область истинных значений заштрихована). Их легко получить из таблиц соответствия для функций двух переменных. Имеют место также соответствия между различными операциями, вытекающие из зависимостей между булевыми функциями: P(x) → Q(x) соответствует P̅(x) ∨ Q(x), P̅(x) ~ Q(x) соответствует (P(x) ∨ Q̅(x)) (P̅(x) ∧ Q̅(x)) или P(x)Q(x) ∨ P̅(x)Q̅(x) и т.п.