5 Немного о методе

Для греческих математиков возможность доказать теорему становится ключевым моментом. Ни одна теорема не может считаться состоятельной, если ее не сопровождает доказательство, иными словами, логичное и точное подтверждение. Крайне важным было суметь предметно продемонстрировать доказательство, т. к. в противном случае оставалось сомнение в совершенстве теоремы и были бы возможны неожиданные сюрпризы. Некоторые методы, несмотря на то что широко известны и повсеместно используются, не всегда хорошо работают.

Вот пример. Помните, в папирусе Ахмеса описывалось, как начертить квадрат и круг с одинаковой площадью? В этих рассуждениях, без сомнения, есть ошибка. Отклонения незначительные, тем не менее они есть. При измерении площадей фигур оказывается, что разница составляет приблизительно 0,5 %! Ну что же, для землемеров такая точность достаточна, однако для теоретиков математики недопустима.

Даже среди гипотез Пифагора были ошибочные суждения. Одно из таких заблуждений касалось соизмеримости длин. Пифагор полагал, что в геометрии любые величины соизмеримы, т. е. всегда можно найти достаточно малую величину для измерения любых двух длин. Представьте два отрезка длиной 9 и 13,7 см соответственно. В Древней Греции еще не использовались десятичные значения для измерений, и, таким образом, второй отрезок нельзя было измерить в сантиметрах. Разумеется, нет ничего сложного в том, чтобы определить длину отрезка единицами в десять раз меньшими, чем сантиметры, соответственно, длины отрезков составят 90 и 137 мм. Пифагор был убежден, что любые два отрезка соизмеримы, и их длины можно определить в соответствующих единицах.

Это утверждение опроверг древнегреческий философ-пифагореец Гиппас из Метапонта. Ученому приписывают открытие существования несоизмеримых отрезков, а именно стороны и диагонали квадрата! Какую бы вы ни выбрали единицу измерения, сторона квадрата и его диагональ не будут соизмеримы в целых выбранных единицах. Гиппас привел логическое обоснование этой гипотезы и не оставил никакого сомнения в ее справедливости. Пифагор и его последователи были настолько сильно оскорблены этим, что исключили Гиппаса из школы. В некоторых источниках даже говорится о том, что ученого сбросили с обрыва в море его ученики!

Математикам эти истории могут показаться ужасающими. Можно ли когда-либо чувствовать себя полностью уверенным? Каково это, жить в постоянном страхе того, что в один прекрасный день математическое открытие оборвет вашу жизнь? И треугольник со сторонами 3–4–5 – в самом ли деле он прямоугольный? Нет ли вероятности, что в один из дней выяснится, что, казавшийся абсолютно прямым, он все же не идеален?

Даже сегодня нередки случаи, когда математики становятся жертвами ошибочных догадок. Именно поэтому, продолжая традиции своих древнегреческих предков, современные математики четко разграничивают суждения, которые могут быть однозначно доказаны, так называемые теоремы, и те из них, которые еще не доказаны, получившие название «гипотезы».

Одной из самых известных гипотез нашего времени является гипотеза Римана. Многие математики опираются на ее справедливость и основывают на ней свои исследования. Если когда-нибудь эта теорема будет доказана, их работа также окажется подтвержденной. Но если ее опровергнут, то и все их труды будут напрасны. Ученые XXI в. намного более благоразумны, чем их предшественники из Древней Греции, тем не менее можно предположить: если кому-то удастся опровергнуть гипотезу Римана, даже в текущих условиях на этого человека вполне предсказуемо обрушится гнев некоторых коллег.

Чтобы избежать этого постоянного страха ожидания опровержения, математикам требуется приводить доказательства. Нет, мы никогда не узнаем о том, что треугольник со сторонами 3–4–5 не является прямоугольным. Это точно. И эта уверенность проистекает из теоремы Пифагора, которая подтверждает это. Любой треугольник, сумма квадратов катетов которого равна квадрату гипотенузы, является прямоугольным. Это суждение было для математиков Месопотамии гипотезой, но благодаря древним грекам оно стало теоремой. Уф!

Так в чем же заключается доказательство? Теорема Пифагора – не только одна из самых известных теорем, она также имеет множество различных доказательств. Их насчитывается несколько десятков. Некоторые из них сделаны представителями цивилизаций, которые даже не слышали о Евклиде или Пифагоре – например, подтверждение встречается в китайском произведении «Математика в девяти книгах». Иные доказательства сформулированы уже после Пифагора – с той лишь целью, чтобы остаться в истории и поупражняться в рассуждениях. Так, среди тех, кто сформулировал собственные доказательства теоремы Пифагора, – знаменитый итальянский изобретатель Леонардо да Винчи, а также двадцатый президент США Джеймс Абрам Гарфилд.

Один из наиболее распространенных принципов доказывания – принцип мозаики: если две геометрические фигуры могут быть сложены из равных элементов, то их площади равны. Обратимся к примеру такого доказательства, которое привел в III в. н. э. ученый из Китая Лю Хуэй.

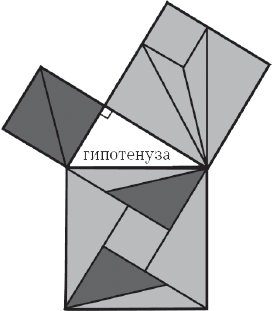
Два квадрата, стороны которых соответствуют катетам, состоят из двух и пяти частей соответственно. Из этих же самых семи частей состоит квадрат со стороной, равной гипотенузе. Площадь квадрата со стороной, равной гипотенузе, таким образом, равна сумме площадей двух других квадратов. И так как значение площади квадрата равно числовому значению квадрата стороны, теорема Пифагора верна.

Для того чтобы доказательство было убедительным, необходимо гарантировать, что все составляющие абсолютно равны по размерам и что это будет верно для любых прямоугольных треугольников.

Попробуем коротко изложить последовательность рассуждений. Почему треугольник со сторонами 3–4–5 прямоугольный? Потому что он подтверждает теорему Пифагора. А почему теорема Пифагора верна? Потому что доказательство Лю Хуэйя подтверждает, что квадрат со стороной, равной гипотенузе, может быть составлен из тех же элементов, что и два квадрата, стороны которых равны катетам. Это все очень напоминает детскую игру в «почему». Проблема этой игры в том, что вопросы никогда не заканчиваются. Каков бы ни был ответ, следом возникает еще один вопрос, начинающийся со слова «почему». Почему? Да, действительно, почему?

Вернемся к нашему примеру: мы утверждаем, что если из одних фигур можно составить другую, то их площади равны. Но как можно убедиться в том, что это действительно так? Что если в зависимости от того, как будут сложены элементы, площади станут отличаться? Такое предположение может показаться абсурдным, не так ли? Настолько абсурдным, что даже странно было бы пытаться это доказывать…

Ситуация непростая. Осложняется она еще и тем, что, даже если нам удастся объяснить, почему принцип мозаики правильный, после этого необходимо будет доказывать справедливость самих аргументов, используемых в целях доказывания!

Математики Древней Греции отдавали себе отчет в существовании этой проблемы. Для того чтобы доказать что-либо, необходимо было от чего-то отталкиваться. Так, первая фраза любого доказывания не может быть доказана как минимум потому, что она первая. Любая математическая конструкция должна начинаться с определенного количества предпосылок, на которых и будут основываться последующие рассуждения.

Такие истины в математике получили название «аксиомы». Как и теоремы и гипотезы, они являются плодами наблюдения математиков, но, в отличие от других двух типов, не требуют приведения доказательств и принимаются как истинные.

«Начала», написанные Евклидом в III в. до н. э., описывают в тринадцати книгах принципы геометрии и арифметики.

О жизни Евклида не сохранилось такого большого количества информации, как о Фалесе или Пифагоре. По одним данным, он жил где-то в районе Александрии. По другим – по аналогии с Пифагором, некоторые историки предполагают, что это вымышленное имя, под которым скрывается наследие нескольких ученых. Наверняка это нельзя определить.

В отсутствии информации о самом ученом человечество получило огромное наследие в виде «Начал», теоретической работы, которая единогласно признается одним из наиболее значительных произведений математики, т. к. именно в нем впервые появилось понятие аксиоматики. Форма написания «Начал» максимально приближена к тому формату, который используется современными математиками. В конце XV в. н. э. «Начала» были среди первых произведений, которые перепечатывались на только что появившемся прессе Гуттенберга. Сегодня произведение Евклида занимает второе по количеству отпечатанных копий место, уступая по этому показателю только Библии.

В первой книге «Начал» Евклида, посвященной, прежде всего, геометрии, была дана следующая система аксиом.

1. От всякой точки до всякой точки можно провести прямую.

2. Ограниченную прямую можно непрерывно продолжать по прямой.

3. Из всякого центра всяким радиусом может быть описан круг.

4. Все прямые углы равны между собой.

5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых углов, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых углов.[7]

Далее приводятся безукоризненные доказательства многочисленных теорем, и для каждого Евклид использует только эти пять аксиом либо результаты, полученные с их применением. Последняя из описанных в первой книге теорем есть не что иное, как теорема Пифагора.

После Евклида многие математики задумывались над вопросом выбора аксиом. Многие из них особенно долго рассуждали над пятой аксиомой. Она куда менее очевидна, чем четыре другие. Часто ее заменяют другой аксиомой, которая позволяет прийти к аналогичным выводам: через точку можно провести единственную прямую, параллельную данной прямой. Дебаты по поводу выбора пятой аксиомы продолжались вплоть до XIX в., когда появились новые геометрические модели, для которых эта аксиома неверна.

Открытие аксиом приводит к еще одной проблеме: проблеме определений. Все эти используемые слова: точки, части, углы, различные круги, – что они обозначают? Так как для приведения доказательств вопрос формулирования определений бесконечен, самое первое определение будет дано с использованием определенных терминов впервые.

В «Началах» определения появляются раньше, чем аксиомы. Первая фраза первой книги – определение точки.

Точка есть то, что не имеет частей.

Как же с этим быть! Этим определением Евклид хотел сказать, что точка – это наименьшая из геометрических фигур. Невозможно разделить на части точку, т. к. она неделима и не имеет частей. В 1632 г. в первом французском издании «Начал» Дени Энрион (Denis Henrion) немного расширил определение, уточнив, что у точки нет ни длины, ни ширины, ни толщины.

Отрицательные определения оставляют возможности для скепсиса. Сказать, чем точка не является, это не то же самое, что сказать, чем она является! И это настолько хитро, что лучше и не придумаешь. В некоторых школьных учебниках начала XX в. можно найти следующее определение: точка – это оттиск, оставленный на листке бумаги абсолютно острым карандашом. Абсолютно острым! В этот раз определение конкретное. От такого определения у Евклида, Пифагора и Фалеса волосы на голове встали бы дыбом, ведь они приложили много сил для того, чтобы сделать из геометрических фигур абстрактные идеальные объекты. Ни один карандаш, как бы хорошо он ни был заточен, не сможет оставить такой оттиск, который не имеет ни длины, ни ширины, ни толщины.

Коротко говоря, никто наверняка не может сказать, что же такое точка, но все согласны с тем, что сама ее природа настолько очевидна, что применение определений может привести к еще большей двусмысленности. Мы в той или иной степени уверены, что говорим об одном и том же, когда используем термин «точка».

Это допущение будет использоваться во всех первых определениях и аксиомах, которые станут базовыми для самой геометрии. И, за неимением лучшего, этот принцип используется во всех математических моделях.

Определения, аксиомы, теоремы, доказательства – путь, проложенный Евклидом, определил принципы работы будущих математиков. Однако, несмотря на то что теории структурировались и становились проще, математики столкнулись с новыми явлениями, которые, подобно песчинкам в ботинке, стали мешать стройности рассуждений: они получили название «парадоксы».

Парадокс – это пример того, что должно работать, но по какой-то причине не работает. И это противоречие необъяснимо. Объяснение, которое кажется абсолютно верным, тем не менее приводит к совершенно невероятному и абсурдному заключению. Представьте себе перечень аксиом, кажущихся вам бесспорными. Однажды вы столкнетесь с теоремой, которая докажет их ошибочность. Кошмар!

Один из самых известных парадоксов связывают с именем Евбулида Милетского и словами поэта Эпименида. Последний заявил однажды, что «все жители Крита – лгуны». Проблема заключается в том, что Эпименид и сам был критянином. Таким образом, если то, что он сказал, верно, то это утверждение ложно… и, следовательно, его слова ложь. А если, напротив, утверждение ошибочно, то он солгал и утверждение верно! Впоследствии появились многочисленные варианты данного парадокса, среди которых один из наиболее простых может быть сформулирован как «я лгу».

Парадокс лжеца ставит под сомнение мысль о том, что любое утверждение не может быть одновременно и верным, и неверным. Третьего не дано. В математике этот принцип получил название «закон исключенного третьего». На первый взгляд, можно было бы принять этот принцип в качестве аксиомы. Однако парадокс лжеца дает нам понять, что ситуация может оказаться не такой очевидной. Если сформулированная закономерность подтверждает свою собственную неверность, с логической точки зрения нельзя признать ее ни верной, ни неверной.

Несмотря на это многие математики и по сей день придерживаются закона исключенного третьего и считают его верным. В конце концов, парадокс лжеца на самом деле не столько математическое наблюдение, сколько лингвистическое несоответствие. Более чем через две тысячи лет после Евбулида логики заметили, что парадоксы такого рода могут также возникать в контексте самых строгих теорий, что, безусловно, заставляло волноваться математиков.

Зенон Элейский, живший в Древней Греции в V в. до н. э., также прославился своими парадоксами. Ему приписывается авторство десятка парадоксов. Один из самых известных – это парадокс Ахиллеса и черепахи.

Представьте забег, в котором участвуют знаменитый своими физическими способностями Ахиллес и черепаха. Чтобы уравнять их шансы, предоставим черепахе фору, скажем, в 100 м. Несмотря на это кажется, что Ахиллес, скорость которого в разы превышает скорость черепахи, рано или поздно обгонит ее. Зенон, однако, убеждает нас в обратном.

Рассмотрим забег в несколько этапов – говорит нам Зенон. Для того чтобы обогнать черепаху, Ахиллес должен для начала преодолеть хотя бы расстояние, отделяющее его от черепахи. Когда Ахиллес пробежит эти сто метров, черепаха уже будет чуть дальше, и, таким образом, Ахиллесу нужно будет пробежать еще и этот интервал, чтобы ее догнать. Но когда он преодолеет этот участок, черепаха окажется еще чуть дальше. Так можно продолжать и продолжать, но черепаха все равно окажется чуть дальше, чем атлет.

Коротко говоря, каждый раз, когда Ахиллес достигает точки, в которой изначально была черепаха, она продвигается чуть дальше. И это остается верным, сколько бы раз ни повторялось! Так, расстояние между ними будет сокращаться, но Ахиллес никогда не догонит черепаху.

Абсурд, не так ли? Достаточно на практике убедиться в том, что бегун без труда обгонит черепаху. Однако с точки зрения теоретической логики ошибки в рассуждениях нет.

Математикам потребуется немало времени, прежде чем будет сделан вывод о том, что этот парадокс есть не что иное, как ловкая игра в бесконечность. Если бы бегуны преодолевали дистанцию, которую Евклид называл отрезком, т. е. ограниченную часть прямой, которая обладает длиной, в то время как он состоит из бесконечного количества точек, не обладающих длиной. Таким образом, мы можем говорить о сочетании бесконечного и конечного. Парадокс Зенона заключается в том, что временные интервалы, за которые Ахиллес преодолевает все новые и новые расстояния, могут быть бесконечно разделены на более мелкие. Если же заменить бесконечность на ограниченное количество времени, то Ахиллес без труда догонит черепаху, когда истечет время.

Понятие бесконечного в математике привело не только к появлению многочисленных парадоксов, но и к формированию самых невероятных теорий.

На протяжении всей истории у математиков было неоднозначное отношение к парадоксам. С одной стороны, они представляют большую опасность. Как только однажды в теории возникает парадокс, все умозаключения ее сторонников и построенные на ее принципах теоремы теряют свой смысл. Но, с другой стороны, какой вызов! Парадоксы – это неиссякаемый источник для новых вопросов и знаний. Наличие парадокса говорит о том, что есть еще что-то, до конца не изученное. Это значит, что мы не до конца поняли явление, плохо сформулировали определение, неверно выбрали аксиому. Это подтверждение того, что вещи устроены иначе, чем мы думали ранее. Парадокс – это приглашение в увлекательное путешествие, повод для обдумывания сущностных идей. Как много новых идей и теорий мы обошли бы стороной, если бы парадоксы не подтолкнули нас к их открытию?

Парадоксы Зенона способствовали тому, что ученые описали концепции бесконечного и измеримого. Парадокс лжеца дал толчок для дальнейших поисков логиками возможностей более наглядного подтверждения своих идей. Даже сегодня многие ученые изучают определенные направления математики, которые зарождались еще в парадоксах древнегреческих ученых.

В 1924 г. математики Стефан Банах и Альфред Тарски явили свету парадокс, впоследствии названный в их честь. Он ставит под сомнение сам принцип мозаики, каким бы очевидным тот ни казался. Банах и Тарски смогли описать разделение мозаики в трехмерном пространстве, в результате чего объем отличался в зависимости от того, каким образом складывались отдельные элементы! Так, выбранные элементы были настолько странными и несуразными, что не имели ничего общего с геометрическими фигурами, которые выбирали древние греки. Можно быть уверенными в том, что принцип мозаики работает в случае с фигурами в форме треугольников, квадратов и иных классических фигур. Доказательство теоремы Пифагора, данное Лю Хуэйем, остается верным.

Но пусть это будет уроком! Не стоит безрассудно брать за основу кажущееся очевидным. Сохраним же интерес к тайнам математического мира, который греческие ученые когда-то открыли для нас.