Глава 3 0,99999999999…

Безусловно, простейший способ записать число один – это цифра 1. Но вы можете столкнуться с тем фактом, что уходящая в бесконечность десятичная дробь 0,999999… представляет собой другой способ записи того же числа. В главе 3 мы присмотримся к этому обстоятельству повнимательнее.

Что означают десятичные числа?

Привычная нам десятичная система счисления удобна и работает отменно, почти без перебоев. Она хорошо подходит для записи целых чисел. 235 – это компактный способ сказать «две сотни, три десятка и пять единиц». Или, на языке математики:

235 = 2 ? 100 + 3 ? 10 + 5 ? 1.

Для некоторых дробных величин десятичная система счисления также чрезвычайно эффективна. Возьмем число 3/4. В десятичной системе его можно записать так: 0,75. Эта запись означает:

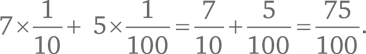
Десятичная дробь 0,75 в точности равна 3/4.

Тем не менее если мы предпримем попытку записать 2/7 в виде десятичной дроби, то потерпим фиаско. Если мы попробуем разделить два на семь с помощью калькулятора, то получим неприглядное 0,28571429, причем это будет лишь приближенное значение, не равное в точности 2/7.

Такие числа, как 3/8, могут быть представлены в виде десятичной дроби, потому что знаменатель в них легко представить в виде одной из степеней десятки: 3/8 = 375/1000. Но нельзя найти целое число A, для которого выполнялось бы условие:

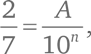
так как это подразумевает 2 ? 10? = 7 ? A. Ни одно целое число A не подходит в качестве решения уравнения, потому что левая сторона не делится на 7, а правая сторона делится. Представить 2/7 в качестве десятичной дроби невозможно. Если только не…

Десятичные дроби с бесконечным числом символов

Идея десятичной дроби с бесконечным числом символов содержит в себе один подвох, и сейчас мы выясним, какой именно. Вернемся к началу главы: что означает 0,99999… и почему оно равно 1?

Для начала давайте представим 0,999999… не как одно число, а как ряд чисел, где каждое следующее – это предыдущее с приделанной справа цифрой 9. Вот как выглядит такой ряд:

0,9 0,99 0,999 0,9999 … (*)

и так далее ad infinitum[38]. Ясно, что элементы ряда (*) постоянно возрастают. Каждый следующий элемент пусть ненамного, но больше предыдущего.

Докажем два факта:

1. Все элементы возрастающего ряда (*) меньше 1.

2. Тем не менее для любого числа x, которое меньше 1, рано или поздно отыщется элемент ряда (*), превышающий x.

Представим элементы ряда (*) в виде обыкновенных дробей:

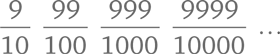
Есть компактный способ записать эти дроби. Знаменатели представляют собой степени десяти: 10¹, 10?, 10? и т. д. Каждый числитель на единицу меньше соответствующего ему знаменателя. Перепишем ряд снова:

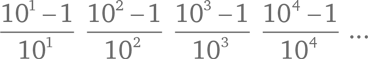
Очевидно, что n-ный элемент ряда будет выглядеть так:

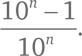
Легко убедиться, что все члены ряда (*) меньше 1, потому что числитель всякий раз оказывается меньше знаменателя.

Теперь докажем второе утверждение: если число x меньше 1, рано или поздно найдется элемент ряда (*), превышающий x.

Так как x меньше 1, разность (1 – x) положительна. Даже если x невероятно близок к единице, разница между ними будет мизерная, но положительная. Умножим (1 – x) на одну из степеней десяти:

10? ? (1 – x).

Так как разность (1 – x) положительна, это произведение будет больше 1, если 10? достаточно велико[39]:

10? ? (1 – x) > 1.

Раскроем скобки:

10? – 10?x > 1,

перенесем 1 в левую часть, а 10?x в правую:

10? – 1 > 10?x,

поделим обе части на 10?:

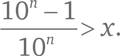
Что мы выяснили? С одной стороны, все элементы интересующего нас возрастающего ряда меньше 1. С другой стороны, какое бы число x меньше единицы мы ни взяли, рано или поздно возникнет элемент ряда, превышающий x (а последующие будут нарастать и все больше удаляться от x).

Наш ряд неуклонно приближается к 1. Математики говорят, что этот ряд стремится к 1. Или, что то же самое, 1 представляет собой предел ряда.

Значение десятичной дроби с конечным числом символов – это сумма определенного количества десятых, сотых, тысячных и т. д. Например:

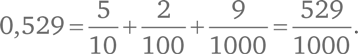
К сожалению, язык десятичных дробей с конечным числом символов слишком скуден, чтобы выразить, например, 2/7. Поэтому нам необходимо расширить лексикон.

Значение десятичной дроби с бесконечным числом символов равно пределу ряда, где на каждой ступени элемент прирастает на одну цифру. Это сложно, однако дает нам возможность выражать все числа, используя десятичную систему счисления.

Уходим в беспредел!

Нужно приложить определенные усилия, чтобы увидеть в бесконечной десятичной дроби предел ряда. Попробуем посмотреть проще.

Вернемся к знакомому нам 0,999999… Пусть:

X = 0,999999… (A)

Умножим обе части равенства на 10:

10X = 9,999999… (B)

Вычтем (A) из (B):

9X = 9,000000…

Теперь поделим обе части на 9 и убедимся, что X = 1. Готово! Все оказалось просто.

Этот фокус можно повторить для любой периодической десятичной дроби. Например:

Y = 0,27272727… (C)

Умножим обе части на 100 (чтобы цифры встали в строй):

100Y = 27,27272727… – (D)

и вычтем (C) из (D):

99Y = 27,000000…

Таким образом, Y = 27/99 = 3/11.

Вот видите[40]! Зачем утруждать себя «сходимостями» и «пределами»? Но с бесконечными последовательностями нужно быть осторожнее. Представим себе сумму:

Z = 1 + 2 + 4 + 8 + 16 + 32 + … (E)

Умножим обе части равенства на 2:

2Z = 2 + 4 + 8 + 16 + 32 + … – (F)

и привычно вычтем (E) из (F):

– Z = 1.

Стало быть, Z = –1? Что за абсурд?

Где мы допустили оплошность? Мы ушли в беспредел. Алгоритм, позволяющий установить значение 0,9999999… и 0,2727272727…, дал сбой, когда мы взялись за ряд 1 + 2 + 4 + 8 + 16… Во всех трех случаях речь шла о бесконечной последовательности. В чем разница? Ответ: в сходимости. Не понимая толком, что такое сходимость ряда, мы запросто придем к выводу, что сумма положительных чисел может быть отрицательным числом. Операции с выражениями (A) и (B), а также (C) и (D) математически корректны, потому что мы имеем дело со сходящимися последовательностями.