Где железнодорожные рельсы пересекаются…

Параллельные линии не пересекаются. Это и делает их параллельными.

Но иногда параллельные линии выглядят так, будто пересекаются. Вспомните о паре железнодорожных рельсов в пустынной местности, которые как будто сходятся в одной точке, по мере того как ваш взгляд перемещается по ним все ближе к горизонту. (По моему мнению, мысленный образ встречающихся друг с другом двух рельсов станет еще ярче, если включить музыку в стиле кантри.) Здесь имеет место феномен перспективы; когда вы пытаетесь отобразить трехмерный мир в двумерном поле зрения, чем-то придется пожертвовать.

Первыми, кто разобрался с этим явлением, оказались люди, которым было необходимо постичь: во-первых, суть объектов; во-вторых, как они выглядят; в-третьих, разницу между реальным объектом и его визуальным образом. Речь идет о художниках. Когда в начале эпохи итальянского Возрождения художники поняли феномен перспективы, визуальное представление изменилось навсегда: с этого момента картины европейских художников перестали напоминать рисунки ваших детей на дверце холодильника (в том случае, если ваши дети рисуют в основном распятого на кресте Иисуса) и стали похожими на то, что на них изображено[215].

Вопрос, как именно флорентийские художники, например Филиппо Брунеллески, пришли к пониманию современной теории перспективы, стал предметом множества дискуссий среди искусствоведов. Мы не будем вдаваться в детали их споров. Но мы наверняка знаем: этот прорыв стал возможен благодаря соединению эстетических соображений с новыми идеями в области математики и оптики. Отправной точкой стало понимание, что изображения, которые мы видим, формируются лучами света, отражающимися от объектов и попадающими в наши глаза. Современному человеку это кажется очевидным, но в те времена, поверьте, было далеко не так. Многие ученые древности – самый известный из них Платон – утверждали, что одним из элементов зрительного восприятия должен быть некий огонь, который испускают глаза. Эта точка зрения восходит как минимум к Алкмеону Кротонскому; считается, что на его мировоззрение повлияло учение Пифагора и пифагорейской школы (о взглядах пифагорейцев шла речь во второй главе). Алкмеон утверждал, что глаза должны испускать огонь, иначе из какого еще источника могут появляться фосфены – звезды, которые вы видите, когда закрываете глаза и надавливаете пальцем на глазное яблоко{187}? Теорию зрительного восприятия посредством отраженных лучей разработал на довольно подробном уровне каирский математик XI столетия Абу Али аль-Хасан ибн аль-Хасан ибн аль-Хайсам аль-Басри (но давайте называть его Альхазеном, как делают большинство западных авторов). Трактат Альхазена об оптике Kitab al-Manazir («Книга оптики») был переведен на латинский язык и с воодушевлением принят философами и художниками, искавшими более систематическую трактовку связи между взглядом и тем, на что он направлен. Основная мысль сводится к следующему: точка Р на вашем холсте представляет прямую линию в трехмерном пространстве. Благодаря Евклиду мы знаем, что существует только одна прямая линия, которая проходит между двумя заданными точками. В данном случае это линия, которая проходит через точку Р и ваш глаз. Любой объект, расположенный на этой линии, необходимо рисовать в точке Р.

А теперь представьте себя Филиппом Брунеллески, стоящим в степи; перед вами холст на мольберте, и вы рисуете железнодорожный путь[216]. Этот путь состоит из двух рельсов, которые мы обозначим R₁ и R₂. Каждый из этих рельсов, нарисованный на холсте, должен представлять собой прямую линию. А подобно тому как точка на холсте соответствует прямой в пространстве, прямая линия на холсте соответствует плоскости. Плоскость P₁, соответствующая рельсу R₁, – это и есть та плоскость, которая образована прямыми, соединяющими каждую точку на этом рельсе с вашим глазом. Точно так же плоскость P₂, соответствующая рельсу R₂, – это плоскость, на которой находится ваш глаз и рельс R₂. Пересечение каждой из этих плоскостей с холстом представляет собой прямую линию; обозначим эти прямые L₁ и L₂.

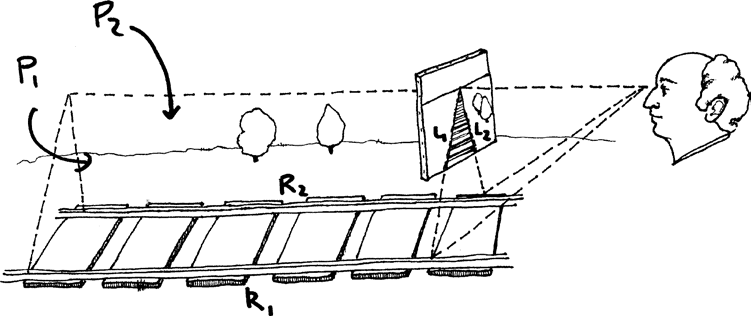
Эти два рельса параллельны друг другу. Однако две плоскости не параллельны. Как они могут быть параллельными? Они ведь пересекаются в вашем глазу, а параллельные плоскости не пересекаются. Плоскости, которые не являются параллельными, должны иметь пересечение в виде прямой линии. В данном случае это горизонтальная линия, которая исходит из вашего глаза и проходит дальше параллельно рельсам. Эта линия, будучи горизонтальной, не пересекается со степью: она стремится к горизонту, не касаясь поверхности земли. Однако (и в этом весь смысл происходящего) она пересекается с холстом в точке V. Поскольку точка V находится на плоскости R₁, она должна быть на линии L₁, вдоль которой рельс R₁ пересекается с холстом. А поскольку точка V находится также на плоскости R₂, она должна быть на линии L₂. Другими словами, V – это точка на холсте, в которой пересекаются нарисованные рельсы. На самом деле любой путь в степи, пролегающий параллельно рельсам, будет выглядеть на холсте как линия, которая проходит через точку V. Точка V – так называемая точка схода, то есть точка, через которую проходят все нарисованные линии, параллельные рельсам. В действительности каждая пара параллельных рельсов образует определенную точку схода на холсте, а положение этой точки зависит от направления параллельных линий. (Исключение составляют только пары прямых линий, параллельных самому холсту, как шпалы между рельсами – на картине они по-прежнему выглядят как параллельные.)

Концептуальный сдвиг, который совершил Филиппо Брунеллески, лежит в основе того, что математики называют проективной геометрией. Вместо точек на местности мы анализируем прямые линии, проходящие через наш глаз. На первый взгляд различие может показаться сугубо семантическим: каждая точка на поверхности земли определяет одну и только одну линию между этой точкой и нашим глазом, так не все ли равно, о чем мы думаем – о точке или о прямой? Разница вот в чем: количество линий, которые проходят через наш глаз, больше количества точек на поверхности, поскольку среди них есть еще и горизонтальные линии, вообще не пересекающиеся с поверхностью земли. Эти прямые соответствуют точкам схода на нашем холсте, то есть тем местам, в которых пересекаются рельсы. Вы можете представить такую линию как точку на поверхности, которая расположена «бесконечно далеко» в направлении рельсов. Математики обычно называют их бесконечно удаленными точками. Если взять плоскость, известную Евклиду, и изобразить на ней бесконечно удаленные точки, получится проективная плоскость. Вот рисунок такой плоскости.

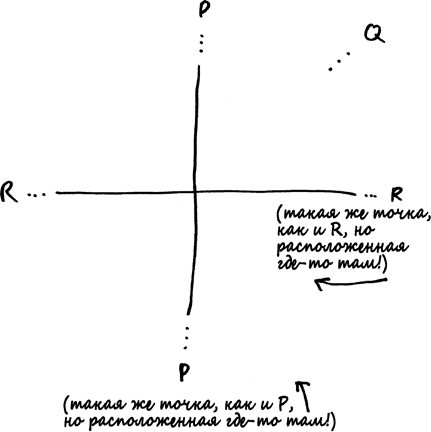
Большая часть проективной плоскости выглядит точно так же, как и обычная плоскость, к которой вы привыкли. Однако на проективной плоскости больше точек: на ней есть так называемые бесконечно удаленные точки – по одной на каждое возможное направление, в котором прямая может быть ориентирована на плоскости. Вы должны представлять себе точку Р, соответствующую вертикальному направлению, как расположенную бесконечно высоко по вертикальной оси, но также и как расположенную бесконечно низко по вертикальной оси. На проективной плоскости два конца оси Y сходятся в бесконечно удаленной точке, поэтому данная ось на самом деле представляет собой не прямую линию, а окружность. Аналогичным образом Q – это точка, расположенная бесконечно далеко на северо-восток (или на юго-запад), а R – точка, которая находится в конце горизонтальной оси. Или, скорее, на обоих концах. Если вы будете перемещаться бесконечно далеко вправо, до тех пор пока не окажетесь в точке R, а затем продолжите идти дальше, то обнаружите, что по-прежнему двигаетесь вправо, но теперь возвращаетесь в центр от левого края рисунка.

Ситуация «отправился по одному пути, вернулся по другому» поразила молодого Уинстона Черчилля, который дал яркое описание одного математического откровения, произошедшего в его жизни:

Однажды я прочувствовал математику, словно обозрел ее всю, все ее глубины раскрылись передо мной, вся ее бездонность. Подобно тому как многие наблюдают за прохождением Венеры или шествием лорда-мэра, я наблюдал за полетом величины через бесконечность и сменой ее знака с плюса на минус. Я понял, почему это происходит и как один шаг влечет за собой все другие. Похоже на политику. Но озарение пришло после плотного ужина – и мне было не до него![217]

По существу, точка R – не просто конечная точка горизонтальной оси, а конечная точка любой горизонтальной линии. Если есть две линии и они обе горизонтальные, значит, это параллельные линии. Тем не менее в проективной геометрии они пересекаются в бесконечно удаленной точке. Дэвиду Фостеру Уоллесу в 1996 году в одном из интервью задали вопрос о концовке романа Infinite Jest («Бесконечная шутка»), который многие считали незавершенным. Журналист поинтересовался у Уоллеса, не уклоняется ли тот от написания заключительной части романа, потому что ему «надоело его писать». Уоллес довольно раздраженно ответил:

Концовка есть, как мне кажется. Считается, что определенные типы параллельных линий начинают сходиться таким образом, что читатель может спроецировать «конец» куда-то за пределы правильной системы координат. Если вы не увидели такого схождения или проекции, значит, книга для вас потеряна{188}.

* * *

У проективной плоскости есть недостаток: ее трудно нарисовать. Но есть у нее и преимущество, делающее правила геометрии более согласованными. На евклидовой плоскости две различные точки определяют одну прямую, а две различные прямые определяют одну точку пересечения, если только они не параллельные – в таком случае они вообще не пересекаются. В математике мы любим правила, но не любим исключений. С проективной плоскостью вам не придется делать никаких исключений в правиле, говорящем, что две прямые пересекаются в одной точке, поскольку параллельные прямые также пересекаются. Например, любые две вертикальные линии пересекаются в точке Р, а две линии, указывающие с северо-восточного направления в юго-западном, пересекаются в точке Q. Две точки определяют одну линию, две линии пересекаются в одной точке, вот и все[218]. Здесь имеет место идеальная симметрия, простота и изысканность, не свойственные классической планиметрии. Совсем не случайно, что проективная геометрия возникла естественным образом в результате попыток решить практическую задачу отображения трехмерного мира на плоском холсте. Как раз за разом показывает история науки, математическая элегантность и практическая полезность идут рука об руку. Порой ученые открывают теорию и предоставляют математикам искать объяснение ее элегантности; в других случаях математики разрабатывают элегантную теорию и оставляют ученым искать области ее применения.

Реалистическая живопись – та область деятельности, в которой применяется проективная плоскость. Еще одна такая область – выбор лотерейных номеров.