Решения задач 1-10

Решения задач 1-10

1. Сторож рассчитал совершенно правильно: ему действительно причиталось даже более трех тысяч возов яблок, как это ни невероятно.

В самом деле. Проследим, как возрастало вознаграждение сторожа с каждым часом.

За 1-й час сторож должен был получить яблоко, за 2-й час – 2 яблока, за 3-й час -4 яблока, за 4-й – 8, за 5-й – 16, за 6-й – 32, за 7-й – 64, за 8-й – 128, за 9-й – 256, за 10-й -512.

Пока еще вознаграждение как будто не грозит арендатору разорением: за первые 10 часов сторожу причиталось всего около по л у тысячи яблок.

Но продолжим исчисление.

За 11-й час сторожу следовало 1024 яблока, за 12-й – 2048, за 13-й – 4096, за 14-й -8192, за 15-й – 16 384.

Накапливается внушительное число яблок, но все же до трех тысяч возов еще далеко.

Далее.

За 16-й час следовало 32 768 яблок.

За 17-й – "– "– 65 536 – "-

За 18-й – "– "– 131 072 – "-

За 19-й – "– "– 262 144 – "-

За 20-й – "– "– 524 288 – "-

Арендатор уже должен сторожу свыше полумиллиона яблок. Но сутки не кончены – остается еще 4 часа.

За 21-й надо было уплатить 1 048 576 яблок

За 22-й – "– "– "– 2 097 152 – "-

За 23-й – "– "– "– 4 194 304 – "-

За 24-й – "– "– "– 8 388 608 – "-

Теперь нужно сложить все эти числа от 1 до 8 388 608. Получаем 16 777 215 яблок. Итак, сторожу за одни сутки следовало согласно уговору почти 17 миллионов яблок! Чтобы только пересчитать такое количество яблок по одному в секунду, понадобилось бы полгода непрерывного счета! Полагая по 10 яблок на килограмм, узнаем, что все причитающиеся сторожу яблоки должны были весить 1 677 721 кг, или 1678 тонн.

Это составило бы вагонов 80, груженных яблоками, или, считая по полтонны на воз, свыше 3000 возов. Не правда ли, можно было найти сторожа и подешевле?

2. Крестьянка не дала поезду отправиться в путь тем, что смазала маслом рельсы впереди паровоза. По скользким рельсам не могут катиться колеса паровоза; они вертятся на одном месте, но не катятся вперед, так как нет трения, благодаря которому колеса словно цепляются за рельсы. Вспомните, как трудно ходить по гладкому льду: ноги скользят, не находя опоры, и мы не можем сдвинуться с места. По той же причине не мог сдвинуться и паровоз.

Когда же машинист уплатил долг, крестьянка «сняла колдовство», посыпав смазанные рельсы песком.

История эта, конечно, могла произойти только в давнее время; на современных паровозах имеются специальные песочницы, из которых машинист с помощью особого приспособления высыпает песок на рельсы, когда они становятся скользкими, например, от дождя.

3. Задача решалась бы очень просто, если бы было известно, сколько времени понадобилось шмелю на перелет из сада в родное гнездо. Этого в задаче не сказано, но геометрия поможет нам самим узнать необходимые данные.

Начертим путь шмеля. Мы знаем, что шмель летел сначала «прямо на юг» в течение 60 мин. Затем он летел 45 мин «на запад», т. е. под прямым углом к прежнему пути. Оттуда «кратчайшей дорогой», т. е. по прямой линии – обратно к гнезду. У нас получился прямоугольный треугольник ABC, в котором известны оба «катета», AB и ВС, и надо определить третью сторону, – «гипотенузу» АС.

Рис. 4. Маршрут шмеля

Геометрия учит, что если какая-нибудь величина содержится в одном катете 3 раза, а в другом – 4 раза, то в третьей стороне – гипотенузе – та же величина должна содержаться ровно 5 раз.

Например, если катеты треугольника равны 3 и 4 м, то гипотенуза равна 5 м; если катеты равны 9 и 12 км, то третья сторона равна 15 км и т. п. В нашем случае один катет равен 3 х 15 мин пути, другой -4 ? 15 мин пути; значит, гипотенуза АС равна 5 ? 15 мин пути. Итак, мы узнали, что из сада к гнезду шмель летел 75 мин, то есть 1¹/₄ часа.

Теперь легко уже подсчитать, сколько времени шмель отсутствовал. На перелеты он потратил:

1 час + ³/₄ часа + 1¹/₄ часа = 3 часа.

На остановки у него ушло времени:

¹/₂ часа + 1¹/₂ часа = 2 часа.

Итого: 3 часа + 2 часа = 5 часов.

4. Поверхность крышки равна произведению длины ящика и его ширины; поверхность боковой стенки равна высоте ? ширину; поверхность передней стенки – высоте ? длину. Таким образом,

длина ? ширина = 120;

высота ? ширина = 80;

высота ? длина = 96.

Перемножим первые два равенства. Получим:

длина ? высота ? ширина ? ширина = 120 ? 80.

Разделим это новое равенство на 3-е:

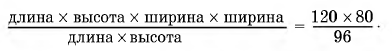
Сократив дробь и произведя действия, имеем:

ширина ? ширина =100.

И, следовательно, ширина ящика равна 10 см. Зная это, легко определить, что высота ящика равна:

80/10 = 8 см,

а его длина = 96/8 = 12 см.

5. Вы не решите этой простой задачи, если не уясните себе сначала, из чего складывается длина цепи. Всмотритесь в рис. 5.

Рис. 5. Звенья цепи

Вы видите, что длина натянутой цепи складывается из полной ширины первого звена, к которой с присоединением каждого нового звена прибавляется не полная ширина звена, а ширина звена без его двойной толщины.

Теперь перейдем к нашей задаче.

Мы знаем, что одна цепь длиннее другой на 14 см и имеет на 6 звеньев больше. Разделив 14 на 6, получаем 2¹/₃. Это и есть ширина одного звена, уменьшенная на двойную его толщину. Так как толщина кольца известна – полсантиметра, то полная ширина каждого звена равна 2¹/₃ + ¹/₂ + ¹/₂ + З¹/₃ сантиметра.

Теперь легко определить, из скольких звеньев состояла каждая цепь. Из рисунка видно, что если мы отнимем от 36-сантиметро-вой цепи двойную толщину первого звена, т. е. 1 см, а разность разделим на 2¹/₃, то получим число звеньев в этой цепи:

35: 2¹/₃ = 15.

Точно так же узнаем число звеньев в 22-дюймовой цепи:

21: 2¹/₃ = 9.

6. Мельник начал с того, что сложил все 10 чисел. Полученная сумма, 1156 кг – не что иное, как учетверенный вес мешков: ведь в нее вес каждого мешка входит 4 раза. Разделив эту величину на 4, узнаем, что пять мешков вместе весят 289 кг.

Для удобства обозначим мешки в соответствии с их весом номерами. Самый легкий мешок получит номер 1, второй по тяжести – 2 и т. д.; самый тяжелый мешок – номер 5. Нетрудно сообразить, что в ряду чисел: 110 кг, 112 кг, 113 кг, 114 кг, 115 кг, 116 кг, 117 кг, 118 кг, 120 кг, 121 кг – первое число составилось из веса двух самых легких мешков, 1 и 2, второе число – из веса мешков 1 и 3. Последнее число есть не что иное как вес двух самых тяжелых мешков, 4 и 5, а предпоследнее – 3-го и 5-го. Итак,

1 и 2 вместе весят 110 кг

1 и 3 – "– "– 112 – "-

3 и 5 – "– "– 120 – "-

4 и 5 – "– "– 121 – "-

Теперь легко узнать сумму весов мешков 1,

2, 4 и 5: она равна 110 кг + 121 кг = 231 кг. Вычтя это число из общей суммы веса всех мешков (289 кг), получаем вес мешка 3, именно 58 кг.

Далее, из суммы веса мешков 1 и 3, т. е. из 112, вычитаем известный уже нам вес мешка 3; получается вес мешка 1: 112 кг – 58 кг = 54 кг.

Точно так же узнаем вес мешка 2, вычтя 54 кг из 110 кг, т. е. из суммы веса мешков 1 и 2. Получаем: вес мешка 2 равен 110 кг – 54 кг = 56 кг.

Из суммы веса мешков 3 и 5, т. е. из 120, вычитаем вес мешка 3, который равен 58 кг; узнаем, что мешок 5 весит 120 кг – 58 кг = 62 кг.

Остается определить вес мешка 4 из суммы весов мешков 4 и 5, т. е. из 121 кг. Вычтя 62 из 121, узнаем, что мешок 4 весит 59 кг.

Итак, вот вес мешков:

54 кг, 56 кг, 58 кг, 59 кг, 62 кг.

7. Мы знаем, что Володя вдвое старше Жени, а Надя и Женя вместе вдвое старше Володи. Значит, годы Нади и Жени, сложенные вместе, вчетверо больше, чем возраст Жени. Отсюда прямо следует, что Надя старше Жени в 3 раза.

Далее, мы знаем, что сумма лет Алеши и Володи вдвое больше суммы лет Нади и Жени. Но возраст Володи есть удвоенный возраст Жени, а годы Нади и Жени, сложенные вместе, есть учетверенный возраст Жени. Следовательно,

годы Алеши + удвоенный возраст Жени = 8-кратному возрасту Жени,

т. е.:

Алеша старше Жени в 6 раз.

Наконец, нам известно, что сумма возрастов Лиды, Нади и Жени равна удвоенной сумме возрастов Володи и Алеши.

Имея перед глазами табличку:

Лиде – 21 год.

Надя – в 3 раза старше Жени,

Володя – в 2 раза старше Жени,

Алеша – в 6 раз старше Жени,

мы можем сказать, что

21 год + утроенный возраст Жени + возраст Жени = 4-кратному возрасту Жени + 12-кратному возрасту Жени,

или:

21 год + 4-кратный возраст Жени = 16-кратному возрасту Жени.

Значит, 21 год равен 12-кратному возрасту Жени и, следовательно, Жене 21: 12 = 1³/₄ года.

Теперь уже легко определить, что Володе 3¹/₂ года, Наде – 5¹/₄ и Алеше – 10¹/₂ лет.

8. Для ясности нарисуем рядом две свечи – толстую, которая сгорает за 5 часов, и тонкую, которая сгорает за 4 часа. Заштрихуем сгоревшие части обеих свечей. Легко сообразить, что длина сгоревшей части тонкой свечи должна составлять ⁵/₄ длины сгоревшей части толстой; другими словами, заштрихованный избыток тонкой свечи составляет по длине ¹/₄ сгоревшей части толстой. Но в то же время длина этого избытка равна ¹/₄ длины толстого огарка. Другими словами, мы узнали, что ³/₄ длины толстого огарка равны ¹/₄ длины сгоревшей части толстой свечи. Значит, ⁴/₄ толстого огарка, т. е. весь огарок, составляет ¹/₄ ? ⁴/₃ ^{= 1}/₃ толстой свечи.

Итак, огарок толстой свечи равен ¹/₃ сгоревшей части или 1/₄ всей длины свечи. Сгорело, следовательно, ³/₄ толстой свечи. А так

Рис. 6. Две свечи – толстая и тонкая как вся свеча могла сгореть за 5 часов, то ³/₄ ее горело в течение

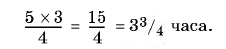
Ответ: свечи горели 3³/₄ часа.

9. Каждый ученик и ученица ежедневно раскланивались со всеми остальными школьниками и с заведующим. С самими собою, конечно, не раскланивались, зато делали поклон заведующему, так что каждый школьник и школьница ежедневно делали столько поклонов, сколько было детей в школе. Значит, все дети вместе ежедневно делали столько поклонов, сколько будет, если умножить их общее число само на себя.

Итак, мы знаем, что 900 – это число детей, умноженное само на себя. Какое же число, умноженное на себя, составит 900? Очевидно, 30. А так как девочек было вдвое больше, чем мальчиков, то из 30 детей было 20 девочек и 10 мальчиков.

Проверим это. Девочки делают 19 ? 20 = = 380 поклонов подругам и 20 ? 10 = 200 поклонов мальчикам. Мальчики мальчикам делают 9 ? 10 = 90 и девочкам – 10 ? 20 = = 200 поклонов. Итого: 380 + 200 + 90 + 200 = 870 поклонов. Присоединив еще 30 поклонов заведующему, имеем ровно 900.

10. Задачу надо решать с конца. Самый младший сын получил столько брильянтов, сколько было сыновей, и еще ¹/₇ остальных; но так как остатка никакого не было, то младший сын получил столько брильянтов, сколько было всех сыновей. Далее, предыдущий сын получил брильянтов на один меньше, чем было сыновей, да еще ¹/7 остальных брильянтов. Значит, то, что получил самый младший, есть ⁶/₇ этого «остального» (а все «остальное» есть ⁷/₇).

Отсюда вытекает, что число брильянтов самого младшего сына должно делиться на 6 без остатка. Попробуем допустить, что их было 6, и испытаем, подходит ли это число.

Если младший сын получил 6 брильянтов, то значит, он был шестой сын, и всех сыновей было 6. Пятый сын получил 5 брильянтов плюс ¹/₇ от 7, т. е. 5 + 1 = 6. Далее, 12 камней есть ⁶/₇, оставшегося после четвертого сына, полный остаток – 14 камней, и четвертый сын получил 4 + ¹/₇ от 14 = 6.

Вычисляем то, что осталось после третьего сына: 18 есть ⁶/₇ этого остатка; значит, полный остаток – 21. Третий сын получил 3 +!/₇ от 21 = 6 брильянтов.

Точно так же узнаем, что на долю второго и первого сына пришлось тоже по 6 камней.

Итак, у раджи было 36 брильянтов и 6 сыновей.

Мы проверили число 6 и нашли, что оно удовлетворяет условиям задачи. Испытав 12, 18 и 24, убедимся, что эти числа не годятся, а больше двух дюжин детей у раджи едва ли могло быть.

Данный текст является ознакомительным фрагментом.