Глава 5 Измерение метра

Глава 5

Измерение метра

В этой главе мы совершим краткий экскурс в историю метра. Сначала мы расскажем, как производились измерения в XVIII веке, с какими трудностями было сопряжено использование множества единиц измерения, а также в каких исторических обстоятельствах появилась универсальная система мер. Мы укажем, какими свойствами должна была обладать новая единица длины, перечислим высказанные предложения и объясним, почему в конечном итоге было принято решение определить новую единицу длины по результатам измерений дуги меридиана. Вы узнаете о математических методах (триангуляции) и измерительных инструментах (повторительном круге Борда), которые использовались при реализации этого проекта, а также о его руководителях (Жан-Батист-Жозефе Деламбре и Пьере Мешене). Кроме того, мы расскажем о приключениях и злоключениях, которые пришлось пережить участникам геодезических экспедиций. В конце главы мы опишем, как проходило распространение метрической системы, а также упомянем некоторые конфликты, связанные с ней.

Потребность в универсальной мере длины

Мы привыкли, что расстояния на указателях автомобильных дорог приводятся в километрах, растительное масло мы отмеряем в литрах, а картофель — в килограммах, но в XVIII веке этих единиц измерения не существовало. Одни и те же величины измерялись разными единицами в зависимости от страны, региона и даже населенного пункта, поэтому при въезде в некоторые города указывались принятые в них официальные единицы измерения.

Приведем несколько примеров единиц длины: вара в Валенсии равнялась примерно 0,906 м, в Теруэле — 0,768 м. Купив несколько вар ткани в Валенсии и продав ее по той же цене в Теруэле, можно было получить прибыль в 18 %. Испанская лига равнялась 5572 м, французская — 3898 м (между прочим, лига упоминается в романе «Дон Кихот» 64 раза). Футы также заметно отличались: испанский равнялся 0,278 м, французский — 0,324 м. Фут — особая единица длины, так как он имеет отношение к испанской железной дороге: согласно королевскому указу от 1844 года, ширина колеи железной дороги равняется 6 испанским футам (6 x 0,278 = 1,67 м). Ширина колеи современных железных дорог в Европе, установленная по образцу английской колеи, равняется 4 английским футам и 8,5 дюймам (1,43 м). Фунт также существовал во множестве вариантов: до учреждения метрической системы в Европе эта единица измерения существовала в 391 варианте.

* * *

КАК ЖЕ МНОГО ЭТИХ ФУТОВ!

Чтобы продемонстрировать, насколько могли отличаться одни и те же единицы измерения, приведем пример антропоморфной меры — фута, который использовался во многих странах, и его соотношение с метром.

Испанский фут: 0,278 м

Французский фут: 0,324 м

Рейнский фут: 0,314 м

Римский фут: 0,297 м

Амстердамский фут: 0,283 м

Швейцарский фут: 0,300 м

Английский фут: 0,304 м

Русский фут: 0,305 м

Египетский фут: 0,225 м

Австрийский фут: 0,316 м

* * *

Обилие единиц измерения и различия между ними в разных регионах затрудняли торговлю и вызывали огромные проблемы при перевозке грузов. Их унификация стала одной из целей Великой французской революции. 9 февраля 1790 года Клод-Антуан Приёр-Дювернуа (1763–1832) по прозвищу Приёр из Кот-д’Ор, военный инженер, отвечавший за реквизирование оружия и боеприпасов на нужды революции, подал по этому поводу петицию в Национальное собрание Франции.

Проект по определению универсальных единиц измерения способствовал не только социальному прогрессу — научное сообщество также видело необходимость определения универсальных мер, и Французская академия наук сыграла в реализации проекта немалую роль. Единицы измерения должны были использоваться для измерения различных величин, которые с точки зрения физики определялись как общие характеристики различных объектов и веществ, например вина и масла. Если требовалось измерить количество вина и масла, то не имело смысла использовать две разные единицы измерения, так как оба этих вещества являются жидкостями — достаточно одной, общей единицы. Спустя несколько лет была введена такая единица измерения — литр.

Одна из основных физических величин — это длина, которая является общей характеристикой для множества объектов и позволяет определить их размеры. Существовало множество мер длины, и казалось логичным начать с определения общей единицы измерения длины. Кроме того, требовались точные инструменты — как для измерения эталона длины, так и для изготовления необходимого числа его копий. Для реализации проекта были все условия: совершенные ранее открытия позволяли изготовить очень точные измерительные инструменты.

При определении требований к новым универсальным единицам измерения решающую роль сыграли идеи равенства, провозглашенные французской революцией. Этих требований было три: во-первых, новые единицы измерения были обязательными к применению во всех странах, во-вторых, они должны были быть неизменными, в-третьих, они не должны были быть антропоморфными.

Выбор меридиана

Какими свойствами должна была обладать новая мера длины? Какие предложения звучали и как было принято окончательное решение? Наконец, почему было решено измерить длину дуги меридиана и какую именно? Ответы на эти вопросы были получены по результатам трех экспедиций, организованных с целью установления метра как универсальной единицы измерения расстояния.

Свойства новой меры длины

Согласно постановлению Французской академии наук, требовалось найти меру длины, которая бы определялась на основе некоего явления природы, так как природа считалась неизменной и принадлежащей всему человечеству. Таким образом удалось бы обеспечить стабильность новой меры и ее неизменность с течением времени.

Но какое явление природы могло стать основой для такой единицы измерения при соблюдении вышеуказанных условий? Было рассмотрено три варианта: первый — длина маятника, второй — длина дуги экватора, третий — длина дуги меридиана.

Какие размеры должна была иметь новая мера длины, чтобы ее было удобно использовать в обычной жизни? В качестве отправной точки была выбрана мера, равная половине туаза. Таким образом, три приведенных выше варианта уже можно было рассмотреть подробнее. Этим занялась комиссия Французской академии наук по просьбе Национального собрания.

Три предложения

8 мая 1790 года, спустя три месяца после того, как Приёр из Кот-д’Ор предложил определить универсальную меру длины, Национальное собрание на своем специальном заседании обсудило различные варианты. Прозвучало два важных доклада, в которых обосновывалась необходимость проведения метрической реформы и определения новой меры длины на основе длины маятника. Шарль Морис де Талейран, председатель собрания и епископ Отёна, предложил считать эталоном длины маятник, отсчитывавший секунды на широте 45°. Во втором докладе, прочитанном самим Приёром из Кот-д’Ор, указывалось, что новая система мер должна быть десятичной. Приёр разделил маятник на три равные части длиной в один фут и описал следующую десятичную систему: фут равнялся 10 дюймам, дюйм — 10 линиям.

Заслушав все доклады, собрание поручило Академии наук изучить высказанные предложения и определить, как следует провести реформу системы мер. Академия, в свою очередь, организовала комиссию, куда вошли самые известные ученые того времени: Пьер-Симон Лаплас, Жозеф Луи Лагранж, Жан-Шарль де Борда, Гаспар Монж и Никола де Кондорсе. 19 марта 1791 года комиссия опубликовала доклад, где были представлены три варианта меры длины, пригодной во все времена и для всех народов:

— длина маятника, половина периода колебаний которого равна одной секунде на 45° широты;

— четвертая часть экватора;

— четвертая часть меридиана.

* * *

ЕДИНИЦЫ ИЗМЕРЕНИЯ В ДЕСЯТИЧНОЙ И ДРУГИХ СИСТЕМАХ СЧИСЛЕНИЯ

Эффективность десятичной системы счисления по сравнению с другими четко проявляется при выполнении расчетов. Так, чтобы найти сумму двух длин, к примеру 3 м + 7 см = 3,07 м или 307 см, в десятичной системе, достаточно перевести одну единицу измерения в другую, умножив или разделив ее на 10 нужное число раз (отсюда и название). Сумму 1 ч 35 мин + 42 мин, напротив, нельзя записать в виде 1 ч 77 мин — правильным ответом будет 2 ч 17 мин, поскольку соотношение между часами и минутами равно не 10 в какой-либо степени, а 60.

В системах счисления, отличных от десятичной, также сложнее выполнять действия с дробями. Рассмотрим 1/4 + 1/2 = 3/4. В десятичной системе

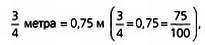
или 75 см, а 3/4 часа = 45 мин. что уже нельзя выразить ни как 75 мин, ни как 7,5, ни какой-либо еще дробью со знаменателем 10, 100 и так далее, так как в этом случае 3/4 = 45/60.

Хотя соотношения между часами, минутами и секундами описываются не десятичной, а шестидесятеричной системой счисления, использовать ее сравнительно просто, поэтому она и сохранилась до наших дней. Пересчет других единиц измерения в иных системах счисления былнамного сложнее, так что с введением метра эти единицы измерения ушли в прошлое.

* * *

Окончательное решение

Французская академия наук поддержала десятичную систему, предложенную Приёром, и склонилась к тому, чтобы из трех предложенных вариантов выбрать в качестве новой единицы измерения длину меридиана. После публикации доклада Академии наук окончательное решение оставалось за Национальным собранием.

26 марта 1791 года Национальное собрание утвердило решение Академии наук и выбрало третий вариант из предложенных. Собрание постановило: «Единицей измерения длины станет четвертая часть земного меридиана, а общеупотребительной мерой длины — десятимиллионная ее часть». На том же заседании было утверждено название новой единицы измерения — «метр» (от древнегреческого 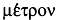 — «мера»).

Почему Академия наук определила метр на основе длины земного меридиана?

К тому времени уже было получено несколько достаточно точных оценок его длины, однако требовалось реализовать намного более масштабный проект, который позволил бы добиться высокой точности измерений, необходимой для определения новой меры. Зачем нужно было начинать намного более дорогостоящий проект, чем тот, в котором метр определялся на основе маятника? Решение комиссии вызвало возмущение некоторых государственных деятелей, в числе которых был и Жан-Поль Марат. Академия наук к тому моменту неоднократно отвергла его научные труды, большинство из которых было посвящено физике.

Комиссия отказалась от измерения экватора, так как производить измерения в малоизвестных областях было затруднительно. Ученые еще помнили, с какими трудностями столкнулась экспедиция в вице-королевство Перу. И все же: почему не маятник — сравнительно удобный и дешевый вариант? Комиссия указала, что единица измерения длины не может зависеть от единицы измерения времени и силы тяготения. Является ли время более «базовой» физической величиной, чем длина? Со временем эти противоречия оказались забыты: в последующих определениях метра, которые точнее соответствовали новым требованиям науки и техники, эти две величины оказались связаны воедино, о чем мы еще расскажем.

По мнению некоторых историков, причина заключалась в том, что один из членов комиссии, Борда, создал очень точный инструмент для измерения углов. Измерение меридиана в конечном счете доказало бы эффективность этого инструмента, и его можно было бы использовать для топографических и астрономических расчетов.

Выбор дуги меридиана

Так как измерить длину четверти меридиана от Северного полюса до экватора невозможно, была предпринята попытка измерить максимально возможную дугу меридиана по суше и экстраполировать результаты. Чтобы компенсировать воздействие рельефа и неидеальной формы Земли, следовало выбрать дугу меридиана вблизи 45-й параллели, такую, что ее концы находились бы на уровне моря, а в середине не было бы высоких гор. Таким образом, требовалось обойти два крупнейших горных хребта Европы — Альпы и Карпаты.

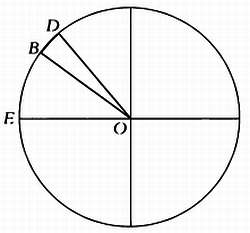
На иллюстрации изображена дуга меридиана, на основе которой был определен метр. Буквой Е обозначен экватор, В — Барселона, D — Дюнкерк.

Были рассмотрены три варианта: Амстердам — Марсель, Шербург — Мурсия и Дюнкерк — Барселона.

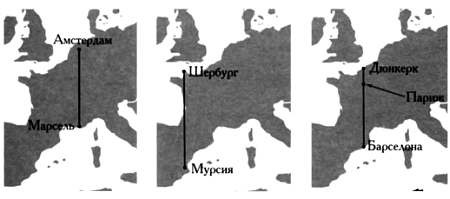
В итоге был выбран третий вариант, так как ранее, в 1739 году, на этом меридиане уже были проведены частичные измерения — так, было измерено расстояние от Дюнкерка до Перпиньяна. Возможно, на решение повлияло и то, что на этом меридиане находился Париж, и именно по этой причине от участия в проекте в 1791 году отказались англичане, которые ранее были готовы сотрудничать.

В апреле 1791 года комиссия Французской академии наук поручила реализацию проекта Жан-Батист-Жозефу Деламбру, Жану Доминику Кассини, Адриен-Мари Лежандру и Пьеру Мешену. Преданный королю Кассини отказался сотрудничать с революционным правительством, заключившим под стражу короля Людовика XVI. 15 февраля 1792 года Деламбр был единогласно избран членом Академии наук. В мае 1792 года, после того как Кассини окончательно отказался участвовать в проекте, Деламбру было поручено возглавить экспедицию на север, из Родеза в Дюнкерк, Мешену — экспедицию на юг, из Родеза в Барселону.

В январе 1806 года, уже после смерти Мешена, Деламбр закончил работу над трехтомным трудом, где были изложены все полученные им данные, условия наблюдений и расчеты, выполненные в ходе триангуляции. Труд носил название «Основы метрической десятичной системы, или Измерение дуги меридиана, заключенной между параллелями Дюнкерка и Барселоны. Выполнено в 1792 и следующих годах Мешеном и Деламбром».

Обложка книги Мешена и Деламбра.

Триангуляция — математическая основа измерения

Два столетия назад измерение дуги меридиана по суше было непростым делом. Измерения производились косвенно и по частям, для этого строилась сеть смежных треугольников, которая покрывала требуемый участок. После построения этой сети треугольников достаточно измерить длину одной стороны треугольника и величины двух прилежащих к ней углов, после чего посредством вычислений можно будет найти стороны всех треугольников в сети. Затем на основе построений в результате новых вычислений определяется длина дуги искомого меридиана. Этот метод называется триангуляцией и используется для измерения площади поверхностей неправильной формы, которые разбиваются на треугольники. Мы подробно описывали его в разделе «Измерение дуг меридианов посредством триангуляции» предыдущей главы.

Сначала отрезок, называемый основанием, измеряется по суше с максимально возможной точностью. Затем строится воображаемый треугольник. Двумя его вершинами будут концы основания, третьей — точка, как правило, находящаяся на возвышении. Она выбирается так, чтобы из каждой вершины треугольника были видны две другие и можно было измерить все три угла треугольника. Зная сторону и углы треугольника, можно вычислить две оставшиеся его стороны, которые, в свою очередь, станут основаниями двух других треугольников. Зная длины этих сторон и измерив углы новых треугольников, можно будет вычислить их стороны, которые станут основаниями новых треугольников. Таким образом, получается последовательность треугольников с известными сторонами. Вершины этих треугольников, называемые геодезическими пунктами, обычно располагаются на возвышениях (на горных вершинах, колокольнях и так далее).

Построенная таким образом последовательность треугольников обладает двумя недостатками: треугольники не располагаются в одной плоскости, а их стороны не сонаправлены с меридианом (мы уже отмечали, что сеть треугольников всего лишь покрывает рассматриваемую дугу меридиана). Следовательно, необходимо построить проекции двух видов, что несколько усложняет расчеты.

Во-первых, стороны треугольников необходимо спроецировать на общую плоскость отсчета. Для этого используется зенитный угол — угол между вертикалью в точке и стороной треугольника, проекцию которого необходимо построить (см. следующий рисунок).

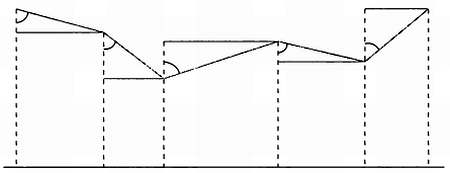
Проекция сторон треугольника на общую горизонтальную плоскость.

Во-вторых, некоторые стороны необходимо спроецировать на меридиан так, чтобы в сумме они покрыли его полностью. Для этого используется так называемый азимутальный угол — между меридианом и стороной треугольника, проекцию которой мы хотим построить.

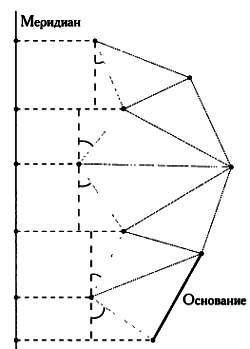
Проекция сторон, покрывающих меридиан.

На суше необходимо определить геодезические пункты — вершины треугольников, которые должны быть видны как минимум из трех других пунктов. Из геодезических пунктов составляется последовательность треугольников, покрывающих меридиан. При триангуляции необходимо последовательно переходить от одного геодезического пункта к другому и измерять горизонтальные углы между соседними пунктами. Далее требуется определить длину стороны одного из треугольников (основание) посредством измерений по суше. Длина основания используется для вычисления длин всех сторон смежных треугольников. Так определяется расстояние вдоль дуги меридиана от самого северного до самого южного геодезического пункта.

Так как измерение угловых расстояний производится с возвышений, необходимо привести все значения к некоторому общему треугольнику, расположенному на плоскости отсчета, как показано на иллюстрации на предыдущей странице.

Измерительные инструменты и точность измерений

Триангуляция требует максимальной точности при измерении основания (длины начального отрезка, на основе которой вычисляются длины сторон всех остальных треугольников) и величин углов смежных треугольников. Чтобы гарантировать точность измерений и избежать накопления ошибок при дальнейших расчетах, важно иметь точные измерительные инструменты и гарантировать, что геодезические пункты четко видны.

Для измерения основания Мешен и Деламбр использовали четыре линейки длиной в два туаза каждая (один туаз равен 1,949 м). Каждая линейка была покрыта слоем платины и меди — так можно было проконтролировать изменение размеров материалов в зависимости от температуры при каждом измерении. Чтобы обеспечить точность измерений, использовалась типографская линейка, показания с которой считывались при помощи лупы. Кроме того, применялись особые устройства, позволявшие укладывать несколько линеек точно в линию и на одном уровне.

Капитан военного корабля и физик-экспериментатор Жан-Шарль де Борда (1733–1799) изобрел оптический прибор для измерения углов — повторительный круг Борда. Этот прибор изготовил Этьен Ленуар, который в то время считался лучшим конструктором измерительных приборов во всей Франции. Повторительный круг Борда позволял измерять один и тот же угол несколько раз без необходимости перемещать прибор. Для измерения углов между геодезическими пунктами требовалось обеспечить оптимальную видимость, что в значительной мере зависело от погодных условий. В некоторых случаях для улучшения видимости применялись лампы, наполненные китовым жиром.

Естественным образом возникает вопрос: какой точности измерений удалось добиться? Были измерены два основания: одно, между Льёэном и Мелёном, — непосредственно для расчетов, второе, между городами Верне и Салз на юге Франции, возле побережья — для проверки результатов. Длина первого основания составила 6075,90 туаза (11,8 км), длина второго — 6006,249 туаза (11,7 км). Длина второго основания, вычисленная на основе первого с использованием сети из 53 треугольников общей протяженностью в 640 км, составила 6006,089 туаза. Ошибка оказалась равной всего 0,16 туаза, то есть 30 см.

Повторительный круг Борда.

Измерение дуги меридиана Дюнкерк — Барселона

Первая экспедиция

Первую и самую известную экспедицию (1792–1799) возглавляли астрономы Жан-Батист-Жозеф Деламбр и Пьер Мешен — ученики Жозефа Жерома Лаланда. Деламбр и Мешен отправились в путь в июне 1792 года. Деламбр, отвечавший за измерение северной части меридиана, выбрал в помощники астронома по имени Мишель Лефранфе, племянника Лаланда, изготовителя инструментов Бенджамита Белле (он был учеником Этьена Ленуара) и слугу по имени Мишель.

* * *

ЖАН-БАТИСТ-ЖОЗЕФ ДЕЛАМБР (1749, АМЬЕН — 1822, ПАРИЖ)

Жан-Батист-Жозеф Деламбр был одним из десяти первых членов комиссии, ответственной за определение метра, созданной 7 Мессидора III года по революционному календарю (25 июня 1795 года по современному календарю).

В состав комиссии также входили Лагранж, Лаплас, Лаланд, Мешен, Кассини, Бугенвиль, Борда, Бюаш и Кароше. После смерти Мешена в 1804 году Деламбр был назначен главой Парижской обсерватории, эту должность он занимал до самой смерти в 1822 году. В 1809 году работа Деламбра об измерении меридиана была удостоена премии Французской академии наук за лучшую научную публикацию десятилетия.

Его перу принадлежат несколько трудов по истории астрономии, в которых особое внимание уделено математическим расчетам: «История астрономии»(1817), «История астрономии в Средние века» (1819) и «Современная история астрономии в 6 томах» (1821). Последний том «Современной истории…» под названием «История астрономии в XVIII веке» был опубликован уже после смерти Деламбра его учеником Клодом Матьё.

* * *

Крайне скрупулезный Мешен отвечал за измерение южной части меридиана (Каркасон — Пиренеи — Кампродон — Пуигсакальм — Матагаллс — Барселона). С ним в путь отправились военный инженер и картограф Жан Жозеф Траншо, изготовитель инструментов Эстевени, учившийся вместе с Ленуаром, и слуга по имени Лебрен. В начале июля 1792 года участники экспедиции достигли Пиренеев, а в октябре добрались до Барселоны. Вся сеть триангуляции изображена в первом томе книги, написанной Деламбром несколько лет спустя.

К чисто геодезическим проблемам прибавились и другие трудности. 1 мая 1793 года Мешен с каталонским ученым Франсеском Сальвой отправился в пригород Барселоны, чтобы понаблюдать за установкой водяного насоса. В результате несчастного случая рычаг длиной почти в два с половиной метра ударил Мешена в грудь и отбросил его к стене; бездыханный Мешен свалился на землю. Доктор Франсеск Сантпонф, лучший хирург города, установил: у ученого раздавлена правая сторона груди, расплющены ребра, в нескольких местах сломана ключица. Даже полгода спустя он по-прежнему не мог пошевелить правой рукой, но, к счастью, позже полностью оправился.

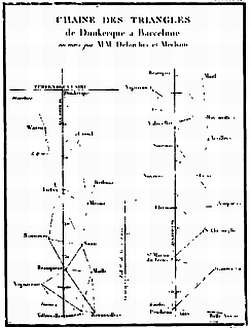
Фрагмент сети триангуляции между Дюнкерком и Родезом, куда входит Париж. Иллюстрация из книги Мешена и Деламбра.

* * *

ПЬЕР ФРАНСУА АНДРЕ МЕШЕН (1744–1804)

Пьер Франсуа Андре Мешен начал обучаться математике в Париже, но из-за финансовых трудностей ему пришлось оставить учебу и давать частные уроки. С ранних лет он занялся исследованиями в области астрономии и географии. Мешен посвятил жизнь тщательным астрономическим наблюдениям. Именно благодаря этому кропотливому труду он был назначен ответственным за измерение южной части дуги меридиана, от Родеза до Барселоны. С 1771 по 1774 год он вместе с Шарлем Мессье (1730–1817) занимался астрономическими наблюдениями и составлением каталогов небесных тел.

Целью наблюдений Мессье были кометы. Чтобы отличить их от других небесных тел, он начал составлять длинный перечень астрономических объектов, часть из которых была открыта Мешеном. Сперва перечень содержал около 40 объектов, но позднее, при содействии других астрономов, разросся до сотни. Этот каталог сегодня известен как каталог Мессье. К удовольствию любителей астрономии, все перечисленные в нем объекты видны на небе в бинокль или небольшой телескоп. В каталоге, разумеется, приведены только объекты, видимые в Северном полушарии, начиная от Северного полюса и заканчивая примерно 35-й параллелью.

* * *

В 1793 году казнь Людовика XVI привела к войне между Францией и Испанией, что также задержало экспедицию.

После завершения триангуляции на территории Испании Мешен попытался вернуться во Францию, но военное командование запретило ему покидать страну. Закрытым для него оказался и замок Монжуик, откуда он ранее производил наблюдения. Мешен провел новые наблюдения из пансионата на улице Эскуделлерс, в котором он остановился, и обнаружил в результатах наблюдений, произведенных с Монжуика, возможную ошибку в 3,24". Эта ошибка не давала ему покоя до самой смерти. Ученый задержался в Барселоне с июня по ноябрь 1794 года, когда ему наконец разрешили вернуться во Францию.

Как и Мешен, Деламбр во Франции также столкнулся с рядом трудностей. Как правило, жители городов и деревень, где проходила сеть триангуляции, не понимали, что задумали эти господа, которые среди ночи подавали с колоколен или горных вершин видимые издалека сигналы. Эти сигналы подавались для того, чтобы избежать некоторых погрешностей измерения, возникавших днем, однако местные крестьяне принимали ученых за шпионов и порой разрушали их конструкции и даже забрасывали исследователей камнями.

Триангуляция в Каталонии. Иллюстрация из книги Мешена и Деламбра.

Вторая экспедиция

Целью второй экспедиции (1803–1804) было продолжение измерений меридиана вплоть до Балеарских островов, в частности до острова Форментера. Решение об организации экспедиции было принято на заседании Бюро долгот 31 августа 1802 года. Вызвано оно было несколькими причинами. Во-первых, чем больше длина дуги меридиана, тем точнее измерения. Во-вторых, при продолжении дуги ее центр оказался бы примерно на 43-й параллели, таким образом, уменьшалась возможная погрешность, вызванная сплюснутой формой Земли. Мешен, который в то время возглавлял Парижскую обсерваторию, настоял на том, чтобы возглавить экспедицию — возможно, ему не давала покоя ошибка, допущенная во время измерений в Барселоне.

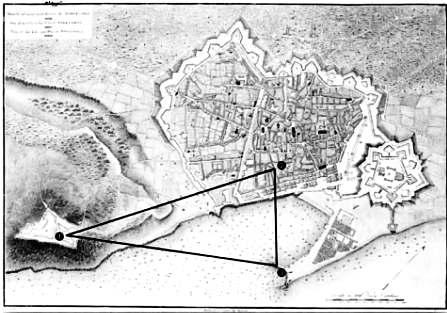
Последняя триангуляция, выполненная Мешеном в Барселоне.

1. Башня клятвы вассалов замка Монжуик. 2. Старинный пансион «Золотой фонтан» (улица Эскуделлерс). 3. Часовая башня в порту.

Часовая башня в порту Барселоны — один из геодезических пунктов последней триангуляции, выполненной Мешеном.

И он действительно возглавил эту экспедицию в Испанию, которая стала для него уже второй. Сопровождали Мешена военный инженер Дезош, бывший ученик Жан-Батист Ле Шевалье, который до этого прожил год в Мадриде, и 18-летний сын Огюстен. Отряд прибыл в Барселону 5 мая 1803 года. В Барселоне к экспедиции присоединились капитан фрегата «La РruеЬа» Энриле, а также заместитель главы Мадридской обсерватории Жозе Каиш. Мешен долго ждал разрешения отправиться на острова, но безуспешно. Тогда он решил подобрать новые геодезические пункты на побережье к югу от Барселоны до района Монсия и осенью провел триангуляцию из Барселоны до различных точек в соседних районах, в частности Гарраф и Монсеррат. На побережье он измерил пять треугольников.

В начале ноября ученый вновь оказался в Барселоне, где наконец смог получить паспорт, но когда фрегат «La РruеЬа», который должен был доставить его к островам, вошел в порт Барселоны, оказалось, что половина команды больна желтой лихорадкой, и судно должно пройти карантин. Рискуя заразиться, капитан Энриле решил вернуться на корабль. В это время Ле Шевалье отправился на юг Испании в поисках древностей, а Каиш убыл в Мадрид. Они оба боялись эпидемии желтой лихорадки, а кроме того, Мешен всячески ограничивал их помощь и не позволял им работать с повторительным кругом.

Чтобы заменить отсутствующих помощников, Мешен обратился за помощью к монаху-тринитарию по имени Агусти Канельес, который представился астрононом. Канельес был уверен в своих знаниях и очень хотел принять участие в исторической экспедиции, так что испанские власти официально назначили его помощником французского астронома.

8 января 1804 года Мешен отплыл на остров Ивиса. Он посетил Ивису и Мальорку, после чего вернулся на Пиренейский полуостров. В августе 1804 года ученый провел измерения на горе Пуиг близ Беникасима и в городе Кастельон-де-лаПлана. Однако Канельес случайно допустил несколько ошибок в записях, и в результате один из сигналов оказался расположен неверно. Чтобы исправить неточность, потребовалось две недели. Скорее всего, именно в это время Мешен подхватил «перемежающуюся лихорадку» (малярию), от которой 20 сентября умер в Кастельоне. Тогда же заболел и Канельес.

Вид города Беникасим с горы Пуиг в провинции Кастельон.

Третья экспедиция

Наконец, состоялась и третья экспедиция (1806–1808), в которой участвовали Био и Араго. В 1805 году математик Пьер-Симон Лаплас предложил Бюро долгот продолжить измерение дуги меридиана до Балеарских островов. Астроному Жан-Батисту Био и юному Франсуа Араго, который был секретарем Парижской обсерватории, было поручено продолжить триангуляцию, начатую Мешеном и не завершенную по причине его безвременной кончины.

В сентябре 1806 года Био и Араго отправились в путешествие в королевство Валенсия. Испанские власти поручили Жозе Каишу (валенсийский астроном и математик, который стал заместителем главы Мадридской обсерватории), участвовавшему в прошлой экспедиции Мешена, и Хосе Родригесу Гонсалесу (галисийский математик, профессор университета Сантьяго) сопровождать членов экспедиции и участвовать в геодезических измерениях. Также в экспедиции участвовал лейтенант флота Манель Вакаро — капитан корабля, который испанские власти предоставили в распоряжение ученых.

Когда участники экспедиции производили измерения в пустыне Лас-Пальмас, как раз в том месте, где заразился лихорадкой Мешен, Жан-Батист Био также заболел и попросил помощи у Антони Марти Франкеса, ученого из Альтафульи (провинция Таррагона), который приютил Био у себя дома, пока тот не выздоровел. В январе 1808 года Био вернулся во Францию, привезя с собой результаты измерений 11 треугольников. Араго принял у него эстафету.

Последний проект Араго заключался в построении сети внутренней триангуляции между Мальоркой и Питиусскими островами, которая должна была охватить острова Мальорка, Ивиса и Форментера. Построение этой сети помогло ученым измерить длину дуги меридиана величиной в три градуса и получить более точные сведения о форме Земли. В апреле 1808 года Араго прибыл на Мальорку и в мае разбил лагерь на горе Мола-де-с’Эсклоп для проведения последних измерений.

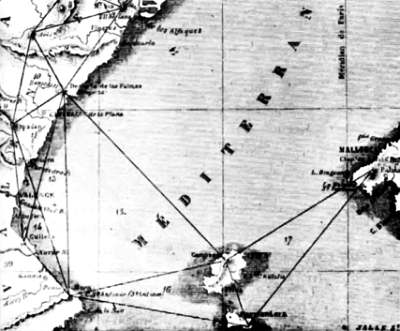
Триангуляция Балеарских островов.

27 мая, в тот самый день, когда Араго проводил последние измерения, на Мальорку прибыли известия о начале Пиренейской войны, что весьма осложнило дело. Как писал сам Араго в автобиографии под названием «История моей юности», благодаря отваге и знанию каталанского языка ему удалось избежать неприятностей.

* * *

ПАМЯТНИК НА ПЛОЩАДИ ГЛОРИАС В БАРСЕЛОНЕ

В честь 200-летней годовщины измерения дуги меридиана Дюнкерк — Барселона прошли различные культурные мероприятия. К примеру, на барселонской площади Глориас был установлен памятник на средства, пожертвованные властями Дюнкерка — города, который по ходу проекта стал побратимом Барселоны. Памятник представляет собой стальную стену длиной 50 метров и высотой 2 метра в наивысшей точке. Он воспроизводит в масштабе воображаемую линию, соединяющую Дюнкерк и Барселону. На ее концах установлены две мраморные таблички, обозначающие Атлантический океан и Средиземное море соответственно. В памятной надписи объясняется смысл памятника на трех языках: каталанском, испанском и французском.

Памятник, установленный в честь измерения дуги меридиана между Дюнкерком и Барселоной.

* * *

Узнав о начале войны, некоторые жители острова сочли, что этот француз, подававший ночью сигналы с вершины Мола-де-с’Эсклоп, был шпионом, они решили схватить его и передать властям. К счастью, Араго помог некий моряк, который заранее предупредил ученого. Араго, переодетый моряком, смог незаметно спуститься с горы, разминувшись с группой вооруженных людей, которые уже шли, чтобы его арестовать. Когда Араго прибыл на корабль, Хосе Родригес Гонсалес, один из его спутников, назначенных испанскими властями, попросил помощи у капитан-генерала, и тот поместил исследователя в замок Бельвер до получения указаний. Спустя несколько дней Араго сбежал из замка и добрался до города Алжира, где сел на корабль, отплывавший в Марсель. Корабль был задержан в море, Араго был отконвоирован в порт Паламос, затем его перевели в Росас, где ученый провел некоторое время. Наконец, 30 августа 1809 года Араго представил Французской академии наук научный труд, в котором были изложены результаты всех проведенных измерений.

Как вводился метр

Появление эталона

Результатом геодезических, астрономических и математических исследований, проведенных под руководством Деламбра и Мешена, стало определение метра как универсальной единицы измерения длины. Пока они проводили измерения, 1 августа 1793 года была введена десятичная метрическая система, а вместе с ней — временный метр, определенный по результатам более ранних измерений.

22 июня 1799 года Национальному собранию был представлен окончательный эталон метра, изготовленный Ленуаром из платины, который пришел на смену временному метру, а также эталон килограмма, определенного как масса кубического дециметра дистиллированной воды при давлении в одну атмосферу и температуре 3,98 °C. Эталоны были помещены на хранение в архивы Республики.

30 августа 1809 года на заседании Бюро долгот, где Араго представил свои расчеты и результаты измерений дуги меридиана от Барселоны до острова Форментера, было проведено сравнение старого и нового метра. Метр, определенный на основе новых данных, менее чем на 5 десятитысячных долей миллиметра отличался от платинового эталона, утвержденного в 1799 году. Ошибка была слишком мала, поэтому платиновый эталон остался неизменным. Лишь спустя 90 лет после его изготовления он был заменен эталоном из платино-иридиевого сплава (90 % платины, 10 % иридия), который был в меньшей степени подвержен деформациям и имел крестообразную форму. Новый эталон был помещен на хранение в Международное бюро мер и весов в городе Севр близ Парижа.

С определением метра родилась метрическая система мер, которую ждал долгий и трудный путь к популярности. Бельгия и Голландия перешли к ее использованию в 1816 году, Испания и Греция — в 1849-м, Португалия — в 1832-м, Германия — в 1870-м, Австрия — в 1873-м, Швейцария — в 1873-м.

Две системы, существующие одновременно

Постепенно новую метрическую систему приняли почти все европейские страны, кроме Великобритании и США.

Когда мы летим в самолете, на небольших экранах на спинках кресел нам указывают траекторию и высоту полета. Высота указывается в футах и (если повезет) — в километрах. В футах (англ, feet) всегда указывается круглое число, в километрах — нет. По какой таинственной причине командир выбирает именно такую высоту? Ответ прост: в самолетах используется английская система мер, где высота измеряется в футах, а скорость — в милях в час.

Если вы поедете в Великобританию на машине, то попадете в похожую ситуацию: на знаках ограничения скорости на автомагистралях будет указано число 70, на обычных дорогах — 50. Если ваш автомобиль родом из континентальной Европы, его руль расположен слева, что очень неудобно при левостороннем движении и обгонах. Вопрос с ограничением скорости прояснится, когда станет понятно, что 70 обозначает мили в час. Если мы произведем пересчет (1 миля = 1609,34 м), то получим, что ограничение составляет 112,6538 км/ч, что куда больше похоже на ограничение в 110 км/ч на наших автомагистралях. Число «50» на знаке, в свою очередь, будет означать 80,467 км/ч.

Фатальная ошибка

23 сентября 1999 года спутник NASA Mars Climate Orbiter должен был закончить полет продолжительностью в 286 дней и приземлиться на поверхности Марса. Однако спутник был потерян из-за несогласованности использованных единиц измерения. Mars Climate Orbiter был разрушен в результате ошибки, которая заключалась в том, что в центре управления на Земле использовалась английская система мер и все данные отправлялись спутнику именно в этой системе, а на самом спутнике расчеты проводились в метрической системе.

Минимальное расстояние, на которое спутник мог приблизиться к поверхности планеты, прежде чем начать заход на посадку, составляло 53 мили — в противном случае он мог быть поврежден под действием высоких температур. Спутник снизился на высоту в 59,54 мили, и казалось, что все идет по плану. Однако на самом деле высота была указана в километрах, и произошла катастрофа: 59,54 больше, чем 53, но 59,54 километра — это всего 37 миль, что намного меньше предела в 53 мили, за которым следовало разрушение спутника.

Mars Climate Orbiter приземляется на Марс 23 сентября 1999 года. Операция завершилась неудачей, так как в программе использовались две разных системы измерения, что привело к разрушению аппарата.

_{(источник: NASA)}