Примечание редактора. Время как четвертое измерение

Примечание редактора. Время как четвертое измерение

Полезно остановиться подробнее на высказанном Уэллсом своеобразном понимании времени как четвертого измерения пространства.

Чтобы уяснить себе это, перенесемся мысленно из знакомого нам мира трех измерений в мир двух измерений. Таким двухмерным миром, имеющим длину и ширину, но вовсе не имеющим толщины, является плоскость. Вообразим же себе, что весь пространственный мир сплющился в одну плоскость и что в таком мире обитают разумные существа, — конечно, также двухмерные. Для двухмерных обитателей существуют только двухмерные вещи. Всякая линия, пересекающая их плоский мир, должна представляться им в виде точки, так как они могут из всей линии воспринять только одну точку — именно ту, в которой эта линия встречает плоскость. Двухмерные существа могли бы исследовать всю эту линию только в том случае, если бы их плоский мир двигался в третьем измерении — например, по перпендикулярному направлению. Наделим этот мир таким движением. Следя тогда за тем, как изменяется положение точки встречи линии с их плоскостью, двухмерные мыслители могли бы составить себе некоторое понятие обо всей трехмерной линии. Но, конечно, они не могли бы так наглядно, как мы, представить себе, какое положение занимает в трехмерном мире эта линия: все трехмерное не укладывается в сознании существа двухмерного. Двухмерный мыслитель высказался бы об этом в других выражениях: он сказал бы, что исследуемая им точка изменяет свое положение во «времени». То, что для нас является движением двухмерного мира (плоскости) в трехмерном пространстве, то для обитателя двухмерного мира представлялось бы как «течение времени». То, что для нас существует одновременно в пространстве трех измерений, — для них появляется последовательно в пространстве двух измерений.

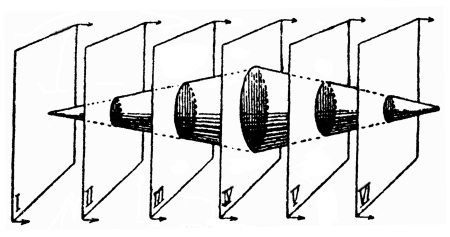
Рассмотрим еще пример. Двухмерный мир (плоскость), двигаясь в трехмерном пространстве, наткнулся на тело в форме двойного конуса (см. рис.). Двухмерный обитатель плоскости, конечно, не может воспринять этот конус как тело; не может даже и вообразить его себе. Что же будет он видеть и думать, когда мир его наткнется на подобное трехмерное тело, и оно пройдет сквозь плоский мир? Проследим за этим. Сначала в двухмерном мире появится точка — вершина конуса. Затем, по мере дальнейшего продвижения плоского мира в направлении третьего измерения (т. е. «с течением времени», как сказал бы двухмерный мыслитель), точка превратится в небольшой кружок или эллипс — сечение конуса плоскостью двухмерного мира. Кружок будет расти, расширяться и, достигнув наибольшего размера, станет сокращаться, постепенно превратится в точку и вновь исчезнет. Двухмерный исследователь наблюдал историю зарождения, развития, увядания и исчезновения «кружка», между тем как мы, существа трехмерные, воспринимаем ту же вещь сразу, одновременно в трех измерениях. Для них он существовал в ряде последовательно воспринимаемых плоских сечений, для нас — весь целиком, как трехмерное тело. Движение плоскости в третьем измерении знакомого нам пространства переживается двухмерным существом как течение времени. Для него «прошедшее» конуса — это те его части, которые лежат по одну сторону его плоского мира (по ту, откуда плоскость движется); «будущее» конуса — те его части, которые расположены по другую сторону, а «настоящее» — пересечение конуса с двухмерным миром.

Приложим теперь те же рассуждения к миру трехмерному. Когда мы описываем историю изменений какой-нибудь вещи в нашем трехмерном пространстве, не даем ли мы последовательные изображения этой вещи во времени? Если так, то можно рассматривать время как четвертое измерение мира, измерение, в котором движется наш трехмерный мир; каждое явление, наблюдаемое в трехмерном мире, есть одно из последовательных «пересечений» нашего трехмерного мира с четырехмерною вещью. Существо четырех измерений могло бы сразу охватить всю историю вещи, всю ее «жизнь» в виде некоторого четырехмерного объекта, недоступного нашему воображению.

Само собою разумеется, что фантастическая мысль Уэллса — придумать механизм для произвольного движения в четвертом измерении — не свободна от внутренних противоречий и должна быть принимаема не иначе как чисто художественный прием, удобный для успешного развития интриги фантастической повести.