Решения задач 31-40
Решения задач 31-40
31. Зрачки на рисунке кажутся движущимися по той же причине, по которой оживают картины кинематографа. Когда мы смотрим на правый рисунок и затем быстро переводим взгляд на левый, то первое зрительное впечатление исчезает не сразу, а еще сохраняется на мгновение; в тот момент, когда оно исчезнет и заменится новым, нам, естественно, должно показаться, что зрачки на рисунке передвинулись от одного края глаза к другому.
32. Все четыре фигуры одинаковой величины, хотя нам и кажется, что они уменьшаются слева направо. В каждой паре правая фигура представляется меньше оттого, что левая расширяется по направлению к правой и словно охватывает ее.
33. Ваше решение, вероятно, было приблизительно таким (рис. 40).
Рис. 40. Кажущееся (неправильное) решение задачи с тремя монетами.
Оно как будто вполне верно удовлетворяет условию задачи, не правда ли? Но попробуйте измерить расстояние циркулем — окажется, что вы ошиблись чуть ли не в полтора раза! А вот правильное расположение монет, хотя на глаз оно кажется совсем неправильным (рис. 41).
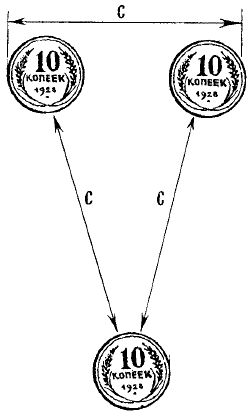
Рис. 41. Правильное решение задачи с тремя монетами.
Чем крупнее кружки, тем обман зрения поразительнее. Опыт хорошо удается и в том случае, если взять неодинаковые кружки.
34. Это интересный обман зрения: фигура человека, идущего впереди, имеет совершенно такую же длину, как и фигура последнего из идущих. Передний человек кажется нам великаном по сравнению с задним только потому, что изображен вдалеке. Мы привыкли к тому, что предметы с удалением уменьшаются; поэтому, видя вдали неуменьшенную человеческую фигуру, мы невольно заключаем (раз она кажется крупной даже на большом расстоянии), что это — человек исполинских размеров.
35. У этих людей ноги вовсе не кривые! Вы можете проверить их прямизну по линейке — все 8 линий идут совершенно прямо и параллельны между собой.
Проверку можно выполнить и без линейки: держите книгу на уровне глаз и смотрите вдоль линий ног, и вы ясно увидите, что ноги прямые.
Кажущаяся кривизна представляет собой любопытный обман зрения, который особенно усиливается, если смотреть на рисунок сбоку.
36. Результат проверки смутит вас потому, что обнаружит грубую ошибочность ответа. Вы, наверное, думали, что окружность пальца раз в 5–6 меньше окружности запястья. Между тем нетрудно убедиться, что окружность запястья всего лишь… в три раза больше пальца! Отчего происходит такой обман зрения — трудно объяснить.
37. Неожиданное явление состоит в том, что через 10–15 сек нижняя белая полоса совершенно пропадает — на ее месте будет сплошной черный фон!
Спустя 1–2 сек полоса снова появится, затем вновь исчезнет, чтобы появиться опять, и т. д.
Это загадочное явление объясняется, вероятно, утомляемостью нашего глаза.
38. Рисунок сделан совершенно правильно. Приложите линейку к канату, и вы убедитесь, что вопреки очевидности его части составляют продолжение одна другой.
39. Линии нисколько не изогнуты ни внутрь, ни наружу, а кажутся вогнутыми внутрь оттого, что их пересекают насквозь несколько дуг.
40. Как ни странно, АС = АВ.
Данный текст является ознакомительным фрагментом.