Решения задач 51-60

Решения задач 51-60

51. Нужно разрезать флаг по ступенчатой линии, обозначенной на рис. 57а.

Теперь остается только передвинуть нижнюю часть флага вверх на одну ступеньку и сшить. Получается флаг уже не с 12 полосами, а с 10, рис. 57б. Он стал более продолговатым, но ни одного клочка материи не пропало.

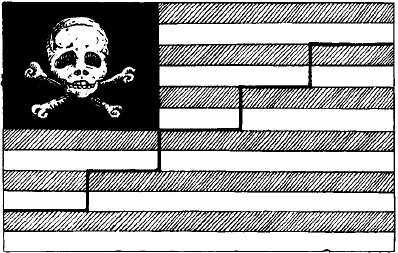
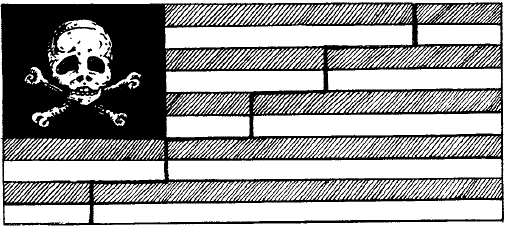
Рис. 57 а, б. Как разрезать и перекроить пиратский флаг.

52. Сестра разрезала квадратный кусок материи на 4 части так, как показано на рис. 58а. Пунктиром обозначены линии разреза от вершин квадрата к середине его сторон.

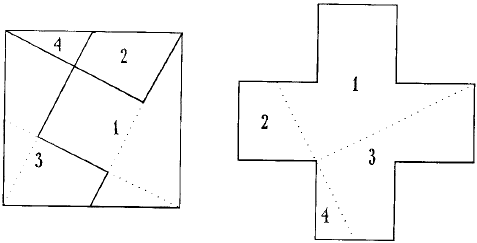
Рис. 58 а, б. Как раскроить квадрат, чтобы из него можно было сшить крест.

Из этих четырех кусков сестра сшила крест (рис. 58 б). Как видите, в нем всего два шва.

53. Вот как сестра сшила крест из обрезков:

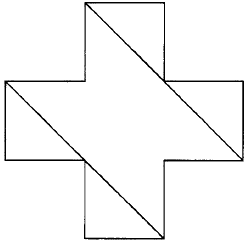
Рис. 59. Как сшить крест из обрезков.

54. Способ, каким сестра вырезала малый крест из большого и составила еще один крест из обрезков, показан на рис. 60.

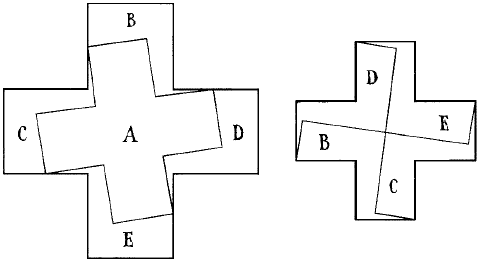
Рис. 60. Как выкроить два малых креста из одного большого.

55. Сделать надо так, как показано на рис. 61. Получаются 6 частей, которые для наглядности пронумерованы.

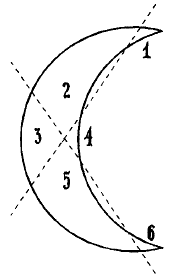
Рис. 61. Как разделить полумесяц (лунный серп).

56. Решение видно из прилагаемого рис. 62. Обе части разделенной «запятой» равны между собой, потому что составлены из одинаковых частей.

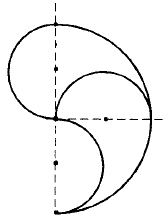
Рис. 62. Как разделить «запятую» на две равные (по площади) части.

Рис. 63 показывает, как составить круг из двух «запятых» — белой и черной.

Рис. 63. Как составить круг из двух «запятых» — белой и черной.

57. Вот все различные развертки куба. Их 12:

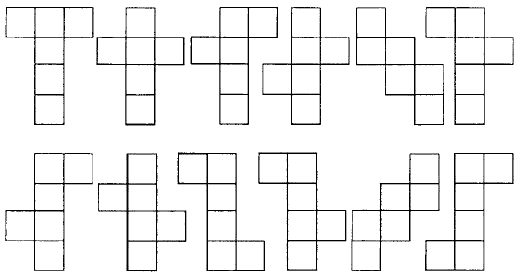
Рис. 64. Развертки куба.

58. Решение первой задачи видно из рис. 65.

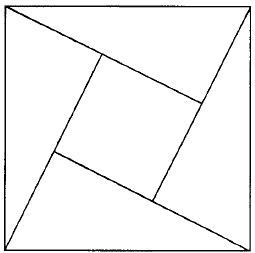
Рис. 65. Квадрат, составленный из четырех треугольников и одного малого квадрата.

А вот как составляется квадрат из 5 треугольников (рис. 66). Один треугольник предварительно разрезают, как показано на рис. 66 б.

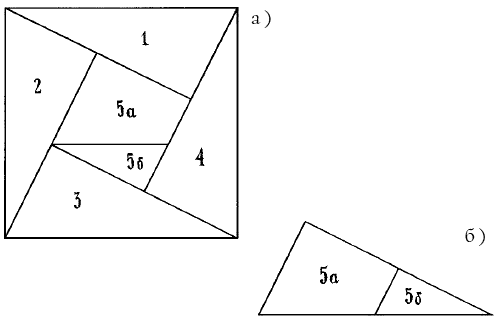
Рис. 66 а, б. Квадрат, составленный из пяти треугольников.

59. Способ раздела земли между четырьмя арендаторами обозначен сплошными линиями на рис. 67.

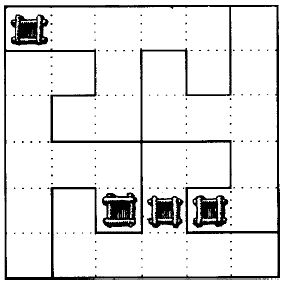
Рис. 67. Раздел земли и колодцев.

Участки получаются довольно причудливой формы, но зато у всех четырех арендаторов они совершенно одинаковы, и у каждого есть колодец.

60. Секрет непонятного исчезновения 64-го квадратика открывается сразу, стоит только тщательнее исполнить рисунок.

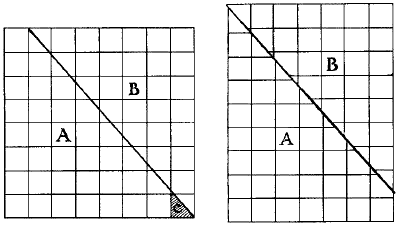
Рис. 68. Тайна исчезнувшего квадратика.

Вглядитесь пристально в приложенный здесь чертеж — вы заметите, что прямоугольник вовсе не составлен из 64 квадратов, как кажется при неотчетливо исполненном чертеже. Те «квадраты», которые расположены вдоль косой линии разреза, совсем не квадраты: каждая из этих фигур по площади немного больше соответствующего квадратика, из суммы этих избытков и слагается недостающая площадь будто бы исчезнувшего квадратика.

Подтасовка выступит яснее, если разграфить фигуру не на 64 квадратика, а всего на 4 х 4 = 16 квадратиков. Наоборот, чем на большее число частей разграфлена фигура, тем труднее уловить ошибку.

Данный текст является ознакомительным фрагментом.