Решения задач 81-90

Решения задач 81-90

81. Удваивая или утраивая четное число, вы всегда получаете в результате четное число. Другое дело с числом нечетным: при удвоении оно становится четным, но при утроении остается нечетным. Гривенник, следовательно, дает четное число и при удвоении, и при утроении; напротив, 3 копейки дают четное только при удвоении; утроенные они дают число нечетное. Мы знаем также, что, складывая четное число с четным, получим четное, а складывая четное и нечетное, получим нечетное число.

Отсюда прямо вытекает, что если в нашем фокусе сумма оказалась четной, значит, три копейки были удвоены, а не утроены, т. е. находились в правой руке.

Если бы сумма была нечетной, это означало бы, что три копейки подверглись утроению и, следовательно, находились в левой руке.

82. Секрет фокуса кроется в том, что второй гость, приписывая к задуманному трехзначному числу то же число, умножил его, сам того не подозревая, на 1001. Действительно, если, например, первый гость задумал число

873,

то у второго гостя получилось число

873873.

Но ведь это не что иное, как

873000 + 873, т. е. 873 ? 1001.

А число 1001 — замечательное число: оно получается от умножения 7,11 и 13. Не удивительно поэтому, что хозяин уверенно предлагал делить такое шестизначное число сначала на 13, потом на 11 и на 7. Делить же последовательно на 13,11 и на 7 все равно, что делить на 13 ? 11 ? 7, т. е. на 1001. Итак, второй гость умножил задуманное число на 1001, а три следующих гостя совместно разделили полученное им число на 1001. Вот почему в результате снова получилось задуманное число.

83. Этот курьезный фокус, в сущности, прост до смешного. Его разгадка ясна, например, уже из того, что если на последний вопрос вам ответит не туз, а валет, успех отгадывания будет не менее блестящим. Вообще, весь секрет фокуса вот в чем: сообразно с тем, что вам нужно, вы сосредоточиваете внимание собеседника либо на тех картах, которые им названы, либо же на тех, которые не названы. А так как задуманная карта непременно должна оказаться либо среди названных, либо среди не названных, то нисколько не удивительно, что собеседник ваш всегда «отгадывает» безошибочно.

Разумеется, когда вы проделаете этот фокус несколько раз подряд, уловка будет раскрыта. Но если не злоупотреблять недогадливостью партнера, то можно поставить в тупик самого находчивого человека.

84. Получаются два кольца, но продетые одно в другое, как звенья цепи (рис. 83). Если каждое из этих колец вы снова разрежете вдоль, то опять получите два кольца, продетые одно в другое.

Рис. 83. Кольцо, разрезанное вдоль средней линии.

85. При разрезании этого кольца вдоль получится, вопреки всем ожиданиям, не два кольца, а… одно, вдвое большее (рис. 84).

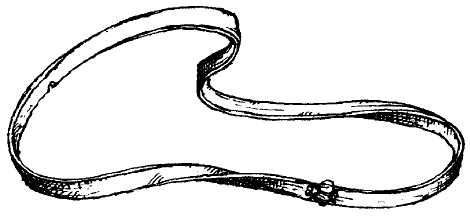
Рис. 84. Другое кольцо, разрезанное вдоль средней линии.

Наша изогнутая лента, обладающая столь удивительным свойством не разъединяться при разрезании, называется в геометрии поверхностью Мебиуса, по имени знаменитого математика прошлого века.

Другая замечательная особенность нашего кольца состоит в том, что у него нет «лицевой стороны» и «изнанки»: «лицо» ленты постепенно переходит в «изнанку», так что невозможно указать, где кончается одна сторона и начинается другая. Если вы пожелали, например, покрасить одну сторону нашей бумажной ленты, скажем, в красный цвет, а другую оставить некрашенной, то не смогли бы выполнить этого: у нашей ленты нет двух сторон, она односторонняя[8].

Но вернемся к разрезанию нашей ленты. Если, разрезав ее вдоль и получив одно кольцо, вы разрежете новое кольцо, у вас получится на этот раз два кольца (рис. 85). Однако разнять их вы не сможете: они запутаны одно в другом сложным гордиевым узлом, который можно рассечь только ножницами.

Рис. 85. Кольцо после двукратного разрезания.

86. Нехитрый секрет беспроигрышной игры найти довольно легко, если попробовать сыграть партию с конца. Нетрудно видеть, что если предпоследним вашим ходом вы оставите партнеру на столе 5 спичек, то выигрыш обеспечен: партнер не может взять больше 4 спичек, и, следовательно, вы возьмете после него все остальные. Но как устроить, чтобы вы наверняка могли в предыдущий ход оставить на столе 5 спичек? Для этого необходимо, делая этот ход, оставить противнику ровно 10 спичек: тогда, сколько бы он ни взял, он не оставит вам меньше 6 — и вы всегда сможете оставить ему 5. Далее, как сделать так, чтобы партнеру пришлось брать из 10 спичек? Для этого надо в предыдущий ход оставить на столе 15 спичек.

Так, последовательно вычитая по 5, мы узнаем, что на столе надо оставить 20 спичек, а еще ранее 25 спичек и, наконец, в первый раз 30 спичек, т. е., начиная игру, взять 2 спички.

Итак, вот секрет беспроигрышной игры: сначала берите 2 спички; затем, после того как партнер взял несколько спичек, берите столько, чтобы на столе осталось 25; в следующий раз оставьте на столе 20, потом 15, потом 10 и, наконец, 5. Последняя спичка всегда будет вашей.

87. Если условие игры обратное, т. е. взявший последнюю спичку считается проигравшим, то вам надо в предпоследний ваш ход оставить на столе 6 спичек: тогда, сколько бы ни взял ваш партнер, он не оставит вам меньше 2 и больше 5, т. е. вы в любом случае сможете последующим ходом последнюю спичку оставить ему. Но как сделать так, чтобы оставить на столе 6 спичек? Для этого нужно в предыдущий ход оставить на столе 11 спичек, а еще в более ранние ходы 16, 21, 26 и 31 спичку.

Итак, вы начинаете с того, что берете всего 1 спичку, а дальнейшими ходами оставляете нашему партнеру 26, 21, 16, 11 и 6 спичек; последняя спичка неизбежно достанется противнику.

88. Здесь разыскать способ беспроигрышной игры несколько труднее, чем при игре в «32». Надо исходить из следующих соображений.

1. Если у вас перед концом партии нечетное число спичек, вы должны оставить противнику 5 спичек, и ваш выигрыш обеспечен. В самом деле: в следующий ход противник оставит вам 4, 3, 2 или 1 спичку. Если он оставит 4 — вы берете три спички и выигрываете, если 3 — берете все три и выигрываете; если 2 — берете одну и также выигрываете.

2. Если же перед концом игры у вас оказывается четное число спичек, то вы должны оставить противнику 6 или 7 спичек. В самом деле, последим, как пойдет дальше игра. Если противник следующим ходом оставляет вам 6 спичек, вы берете одну и, обладая теперь уже нечетным числом спичек, спокойно оставляете противнику 5 спичек, с которыми он должен неизбежно проиграть. Если он оставит вам не 6, а 5 спичек, берете 4 и выигрываете. Если оставит 4 — берете все четыре и выигрываете. Если оставит 3 — берете две и выигрываете. И наконец, если оставит 2 — вы тоже выигрываете. Меньше двух он оставить не может.

Теперь уже не трудно найти способ беспроигрышной игры. Он состоит в том, чтобы имея нечетное число спичек, оставлять противнику на столе такое, которое на 1 меньше кратного 6, т. е. 5, 11, 17, 23; имея же четное число спичек, оставлять противнику на столе число спичек, кратное 6, или на 1 больше, т. е. 6 или 7, 12 или 13, 18 или 19, 24 или 25. Нуль можно считать четным числом; поэтому, начиная игру, вы должны взять из 27 спичек 2 или 3, а в дальнейшем следовать описанной схеме. Ведя так игру, вы неизбежно выиграете. Не давайте только противнику перехватить у вас инициативу.

89. Если условие игры обратное и выигравшим считается обладатель нечетного числа, вы должны поступать при игре следующим образом: имея четное число спичек, оставляйте противнику на 1 меньше, чем кратное 6, имея же нечетное число, оставляйте ему кратное 6 или на 1 больше. Такая тактика обязательно приведет вас к выигрышу. Начиная игру, вы имеете 0 спичек (т. е. как бы четное число), поэтому первым ходом берете 4 спички, оставляя противнику 23.

90. Вы, вероятно, пытались составить шесть треугольников, располагая спички в одной плоскости. И, конечно, безуспешно, потому что так задачу решить невозможно. Но ведь такого ограничения в задаче нет: вы можете располагать треугольники и не в одной плоскости, т. е. размещать их в пространстве. И тогда она решается очень просто — нужно лишь построить из 6 спичек пирамиду с треугольным основанием и треугольными боками (рис. 86). У вас получится 4 равносторонних треугольника из 6 спичек.

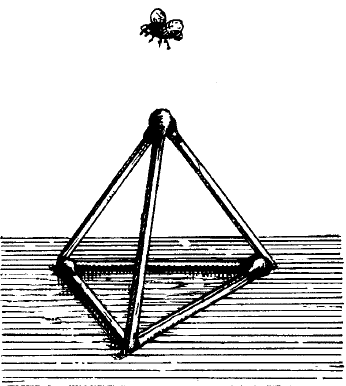
Рис. 86. Четыре равносторонних треугольника из шести спичек (треугольники — грани пирамиды).

Данный текст является ознакомительным фрагментом.