1. Вероятность потери связи в мини-сети

Рассмотрим мини-сеть как в примере, приведенном в главе: три компьютера – 1, 2, 3 и три канала связи: 1–2, 1–3, 2–3. Допустим, что канал связи доступен с вероятностью р и недоступен с вероятностью 1 ? p, где 0 < p < 1. Предположим, что каналы независимы друг от друга. Связь между всеми тремя компьютерами сохраняется в двух случаях.

Случай 1. Все три канала связи доступны. Соответствующая вероятность равна

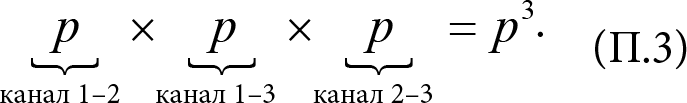
Вероятности перемножаются потому, что каналы независимы друг от друга. Допустим, у нас тысяча мини-сетей и p = 0,6. Тогда примерно в 600 из них будет доступен канал 1–2. Поскольку доступность канала 1–2 никак не влияет на канал 1–3, из нашей 1000 сетей оба канала 1–2 и 1–3 будут доступны в среднем 600 ? 0,6 = 360 случаев. Чтобы вычислить среднее количество сетей, в которых доступны все три канала, надо взять долю 0,6 от 360, получаем 360 ? 0,6 = 216. В результате вероятность доступности всех трех каналов равна

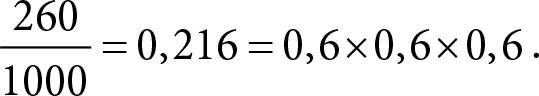
Случай 2. Два канала связи доступны и один недоступен. Недоступным может быть любой из трех каналов связи, поэтому случай 2 можно получить тремя разными способами. В результате соответствующая вероятность равна

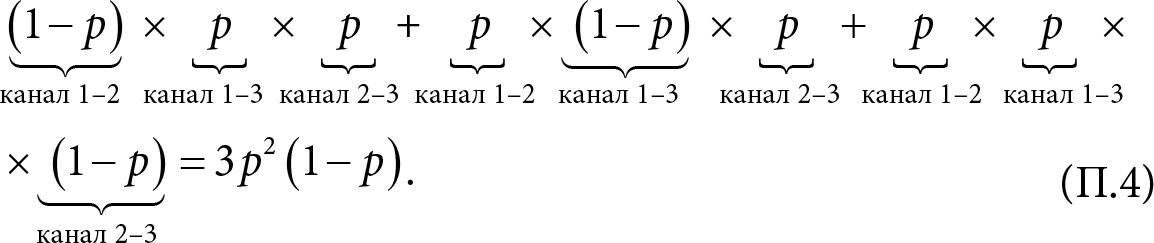
Общая вероятность сохранения связи в сети теперь равна

(П.3) + (П.4) = p? + 3p? (1 ? p) = 3p? ?2p?.

Потеря связи хотя бы с одним из компьютеров тоже происходит в двух случаях, которые мы назовем случай 3 и случай 4.

Случай 3. Два канала связи недоступны и один доступен. Заметьте, что этот случай совершенно аналогичен случаю 2, только р и (1 ? p) поменялись местами. Соответствующая вероятность равна

3 (p ? 1)? p. (П.5)

Случай 4. Все три канала связи недоступны. Этот случай опять же аналогичен случаю 1, если поменять местами р и (1 ? p). Соответствующая вероятность равна

(1 ? p)?. (П.6)

Вероятность, что хотя бы один компьютер окажется отрезанным от сети, равна

(П.5) + (П.6) = 3(1 ? p)? ? 2(1 ? p)?. (П.7)

Естественно, если просуммировать все вероятности, то получится единица. Это очень красиво следует из бинома Ньютона третьей степени:

(П.3) + (П.4) + (П.5) + (П.6) = p? + 3p? (1 ? p) + 3(p ? 1)? p + (1 ? p)? = (p + (1 ? p))? = 1? = 1

Если провести еще немножко алгебраических манипуляций, то можно переписать вероятность (П.7) по-другому:

3(1 ? p)? ? 2(1 ? p)? = (1 ? p)? (3 ? 2(1 ? p)) = (1 ? p)? (1 + 2p) = (1 ? p) ((1 ? p) (1 + 2p)) = (1 ? p) (1 + p ? 2p?)

Легко проверить, что если p > ?, то вторая скобка меньше единицы. Получается, что если p > ?, то вероятность потери связи в мини-сети меньше, чем вероятность потери связи в отдельно взятом канале, которая равна (1 ? p).

Кроме того, выражение (П.7) всегда меньше, чем 3 (1 ? p)?. Поэтому если вероятность неисправности канала (1 ? p) уменьшается, то вероятность потери связи в сети уменьшается еще быстрее. Когда вероятность (1 ? p) очень мала, то термином ?2 (1 ? p)? можно пренебречь. Тогда вероятность потери связи в сети приблизительно равна 3 (1 ? p)?. Если (1 ? p) = 0,01 (то есть 1 %), то эта формула верна до третьего знака после запятой, что мы и видим в последней строчке табл. 4.1.