2. Дискретное логарифмирование

Вспомним, что логарифм числа у по основанию g – это такое число х, для которого выполняется

g^x = y.

Легко заметить, что очень похожая операция лежит в основе схемы Диффи – Хеллмана.

После возведения в степень мы берем остаток от деления на р. Как мы уже упоминали выше, в математике такая операция обозначается g^x (mod p) (читается «g в степени х по модулю р»). При этом, естественно, g и х натуральные числа и у g нет общих делителей с р.

Одна нетривиальная теорема из теории чисел (см., например,{35}) утверждает, что для каждого простого р существует такое число g, что все числа

разные, то есть служат перестановкой множества 1, 2, …, p ? 1 (среди них нет нуля, поскольку g < p и, значит, g^х не делится на р). Например,

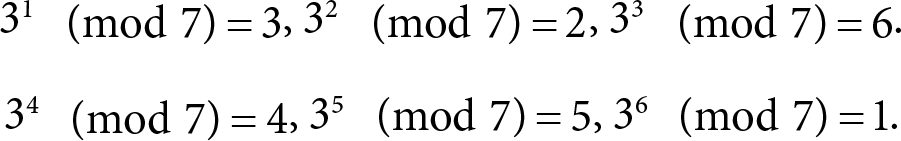
Из этого следует возможность корректного определения дискретного логарифма, который еще называется индексом. А именно: «логарифм» произвольного числа y ? {1, 2, …, p ? 1} по основанию g – это тот самый, уникальный, x ? {1, 2, …, p ? 1}, при котором выполняется g^x (mod p) = y. Поскольку для всех x < p остатки разные, то х определяется однозначно. Операция нахождения такого х называется операцией дискретного логарифмирования. Она очень сложная, и никто не знает, можно ли придумать способ ее быстрой реализации.

Как определить такое число g, чтобы все остатки в выражении (П.15) были разные? Число g обладает этим свойством, если оно является первообразным корнем числа р. Мы позволим себе рассказать об этом понятии немножко подробнее.