1. Схема Диффи – Хеллмана

Для начала введем обозначения. Пусть р – заданное простое число, g – заданное натуральное число, g < p. На самом деле g это так называемый первообразный корень числа р. Об этом мы расскажем ниже, в приложении 2 и приложении 3 к главе 6. Цель данного раздела – доказать, что в схеме Диффи – Хеллмана Алиса и Боб действительно получают один и тот же ключ.

Для любых натуральных чисел n и р мы воспользуемся стандартным обозначением для остатка от деления n на р:

n(mod p) = [остаток от деления n на p].

(Читается «n по модулю p».)

Итак, Алиса задумала число х, а Боб число у. Схема Диффи – Хеллмана состоит из двух шагов.

Шаг 1. Алиса передает Бобу

a = (g^x) (mod p).

Боб передает Алисе

b = (g^y) (mod p).

Шаг 2. Алиса вычисляет ключ

K_A = (b^x) (mod p).

Боб вычисляет ключ

K_B = (a^y) (mod p).

Утверждение. Боб и Алиса получили один и тот же ключ K = K_A = K_B.

Доказательство. Нам нужно доказать, что K_A = K_B. Поскольку а и b – это остатки от деления на р, то существуют такие целые числа k и l, при которых

a = g^x ? kp, b = g^y ? lp.

Подставив эти выражения в формулы для ключей, получаем:

K_A = (g^y ? lp)^x (mod p),

K_B = (g^x ? kp)^y (mod p).

Заметим, что в выражении для K_A можно расписать (g^y ? lp)^x следующим образом:

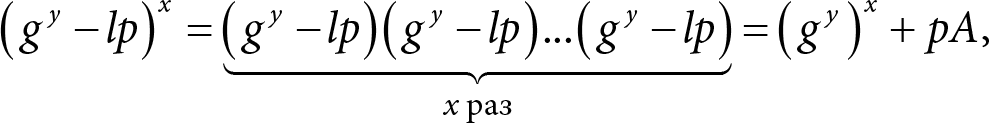
где А – это целое число, то есть рА делится на р. Таким образом получаем

K_A = ((g^y ? lp)^x) (mod p) = ((g^y)^x + pA) (mod p) = (g^y)^x (mod p).

Совершенно аналогично для какого-то целого числа B получаем

K_B = ((g^x ? kp)^y) (mod p) = ((g^x)^y + pB) (mod p) = (g^x)^y (mod p).

Результат теперь очевиден, поскольку

(g^y)^x = g^yx = g^xy = (g^x)^y.