Глава 7 Неевклидова геометрия. Решение
Глава 7
Неевклидова геометрия. Решение
На 1911 год библиография по неевклидовой геометрии составляла список в 4200 работ. Сейчас это число, можно думать, приближается к 20–25 тысячам.
Из них не меньше тысячи трудов историко-биографического характера.
К сожалению, я не нашел точных цифр, но оценки, приведенные выше, основаны на столь жестких гипотезах, что реальные цифры должны быть существенно выше.
Примем за основу тысячу.
Вероятно, не менее двухсот книг и статей посвящены исключительно Лобачевскому.
Спрашивается: зачем же еще?
И автор должен признаться, что трагический вопрос этот не раз и не два возникал во всем своем грозном величии до начала работы, в ее процессе и после ее окончания.
Можно, конечно, утешаться тем, что проблемы подобного сорта неизменно возникают, о чем бы ты ни взялся писать.
И они не слишком оригинальны.
Примерно в 1968 году до н. э. неведомый древнеегипетский пессимист и скептик уныло сетовал: «О если бы я мог сказать нечто такое, что уже многократно не говорилось бы до меня!»
Но утешение это малое. Тем более что за четыре тысячи лет поток печатных строк почти затопил человечество, хотя, если верить классикам, истинно великая книга создается раз в столетие. Однако подобными категориями разумному человеку средних лет (примерно таким представляет себя автор) мыслить не приходится.
И тогда волей-неволей нужно ответить самому себе: «Зачем?»
Что могу добавить я — автор этой книги — ко многим и многим томам, посвященным истории геометрии вообще, неевклидовой геометрии и общей теории относительности в частности?
Во-первых, поставим довольно неприятную точку над «и». Эта книга поверхностна. Предельно поверхностна. Она и не может быть иной.
Даже отбросив чисто специальные вопросы, нужно было бы затратить года два напряженного каждодневного труда, чтобы перерыть и просмотреть главнейшие биографические источники. Но этого, безусловно, недостаточно. Добросовестный и серьезный биограф должен внимательно изучить все работы тех людей, о которых идет разговор, должен кропотливо исследовать реакцию их научных собратьев, должен… бог его знает, что он еще должен.
Кстати, у Лобачевского такой биограф есть.
Академик В. Ф. Каган написал великолепную и серьезную биографию Лобачевского. Правда, быть может, слишком серьезную. Она написана не очень доступно.
Как дилетант в математике (а также по многим другим причинам), я понимал, что не смогу конкурировать в смысле серьезности и квалификации с В. Ф. Каганом. А также с многими другими биографами и исследователями как Лобачевского, так и других ученых, о которых идет здесь речь.
Так зачем все же я пишу?
Знать это было совершенно необходимо. Иначе все эти листы не были бы написаны. (Возможно, это и был наилучший вариант.)
Но я утешил себя тем, что никто еще не писал обо всех героях этой истории как о людях. Не как о величайших, гениальнейших… и т. п. математиках, а как о нормальных (точнее — почти нормальных) людях.
И конечно, я пытался написать так… чтобы передать все… что… Короче, как вы видите, от полноты чувств автор не в состоянии продолжать.
Вот обо всем этом «он» и пытался написать здесь.
И о работе.
О настоящей работе настоящих мужчин.
Как автор-популяризатор, я не могу упустить возможность использовать заслуженную и проверенную (особенно для молодежной литературы) терминологию.
Сильные мужчины уверенно идут по экранам и страницам.
Сильные мужчины бьют морды нехорошим негодяям и покоряют очаровательных девушек с тонкими спортивными фигурками и неспортивным интеллектом.
Сильные мужчины приезжают из глухих деревень в столицу и покоряют ее, как и девушек.
Сильные мужчины уезжают из столицы в провинцию и покоряют ее так же, как… (см. выше).
Сильные мужчины скрывают сильные чувства под маской незначительных внешне слов.
Сильные мужчины порой сильно выпивают в крайне тяжелую минуту; это обязательно, но нехарактерно.
Сильные мужчины покорили всех и вся, и посему автор тоже обуреваем стремлением писать о настоящих мужчинах.
Настоящих. А не о героях, скажем, Эриха Марии Ремарка, которого, да простится мне, я недолюбливаю и полагаю несколько дамским писателем. Пишет, впрочем, он свободно и увлекательно, а «На Западном фронте без перемен» — просто прекрасная книга.
Я еще раз прошу прощения, что отдаю дань моде и ввязываюсь в литературные дискуссии, но, честно признаюсь, довольно утомительны сильные разочарованные герои, кочующие по искусству уже несколько тысяч лет.
Действительно, прародитель этой когорты, пожалуй, вавилонский Гильгамеш.
Итак, о работе.
И о людях. Все это уже я вроде бы объяснял раньше. Но ничего, можно повториться. Именно о людях, а не о гениях.
«Гениев» я тоже не слишком люблю.
Но существует закоренелая, неистребимая традиция. Когда начинают писать о Лобачевском, Эйнштейне, Гауссе, то со страниц так и светит тот самый голубой, преданный блеск глаз, что вспыхивал в глазах Кисы Воробьянинова при общении с Остапом Бендером.
Преклонение это в общем продиктовано хорошими чувствами, и, бесспорно, люди эти, как правило, заслужили его.
Наконец — спешу оправдаться — я и не думаю сопоставлять О. Бендера с Гауссом, например.
Тем не менее подобный стиль унижает и автора, и читателя, и ученых.
А если эти ученые (вспомним старика Пифагора) нуждаются в подобных биографиях, то пусть их пишет кто-нибудь еще. У меня нет к ним ни уважения, ни симпатии.
Я рискну высказать предельно оригинальную мысль.
В первую очередь человек должен быть человеком. И даже такая мелочь, как тяжелый и вздорный характер ученого, может погубить всю симпатию к нему.
Так я сам не могу понять, какие чувства вызывает у меня Янош Бояи[4]. Поэтому начнем с него.
Дарование его поразительно. Необъяснимо. Оно блещет во всем. Один только стиль его работы показывает — это математик «милостью божией». В начале XX века примерно так будут писать работы по математической логике. Ни одного лишнего слова. Предельная сжатость. Безукоризненная логика. Исключительная ясность мысли. В центральном для всей проблемы вопросе, в вопросе о непротиворечивости неевклидовой геометрии, он ушел дальше и Гаусса и Лобачевского. По существу, он очень близок к основной идее доказательства. Он не нашел его, но зато ясно понимает, как, на каком пути надо искать.
Здесь он превосходит всех.
Вполне возможно, что для себя идеи неевклидовой геометрии он сформулировал раньше, чем Лобачевский. Примерно в 1823 году.
Правда, в печати его работа появилась на два года позже, чем первая работа Лобачевского (1831 г.).
Но, вообще говоря, подобные изыскания можно предоставить любителям приоритетных споров.
В конце концов еще раньше немецкий юрист (одно время профессор права Харьковского университета) Фердинанд Швейкарт владел основными элементарными представлениями неевклидовой геометрии. Он, правда, вообще ничего не публиковал, но его племянник Тауринус, которого он соблазнил этой проблемой, даже напечатал брошюру.
Тауринус, хотя и был несравненно более слабый математик, чем главные персонажи этой пьесы, очень близко подошел к решению. Он развил неевклидову геометрию довольно подробно, решил много тонких задач, но ясного понимания у него все же не было. Под конец он приходит к обычному итогу для исследователей пятого постулата — пытается доказать его, а значит, и справедливость евклидовой геометрии.
Это удивительно, потому что одновременно он как будто отлично понимает непротиворечивость своих неевклидовых построений, но…
Раньше мы уже говорили, что, по сути, для создания неевклидовой геометрии нужна была единственная идея, только одна мысль. А к теоремам неевклидовой геометрии неизбежно приходил всякий, кто начинал доказывать пятый постулат «от противного». Например, сам Лобачевский писал о Лежандре:
«Нахожу, что Лежандр несколько раз попадал на ту дорогу, которую я выбрал столь удачно».
Но как раз основной идеи у Лежандра не было. Этой единственной мысли у математиков вообще не было более двух тысяч лет.
Она впервые как неосознанное еще сомнение проскальзывает у Ламберта, она смутно звучит у Швейкарта и Тауринуса, к ней давно уже молча склоняется Гаусс… но только у Бояи и Лобачевского она формулируется ясно и четко.
И по строгости и глубине первая (и единственная) работа Бояи превосходит всех.
Позже, напряженно работая, Лобачевский исследует неевклидову геометрию несравненно более широко и подробно, но, если сравнивать первые работы, более яркое впечатление оставляет Бояи.
Блеск дарования виден во всем.
Он не только гениальный математик. Он исключительно одаренный музыкант. В десять лет он уже автор собственных композиций. Позже — великолепный скрипач высокого профессионального уровня.
Но таланты Бояи еще не исчерпаны. Он был, видимо, один из лучших фехтовальщиков страны. Это далеко не просто в любой стране, а в Венгрии особенно.
Наконец, по своим общественным взглядам Бояи несравненно ближе нам, чем остальные действующие лица.
Враг всякого национализма, горячий сторонник венгерской революции 1848 года, много и напряженно размышляющий над проблемами общественного устройства. Он был очень близок к идеям утопического коммунизма. К концу жизни он задумал построить математическую теорию идеального государства, рассчитывая, что найдет безошибочный рецепт всеобщего счастья.
«Теория» так и называлась: «Учение о всеобщем благе».
А в математике он сочетал холодный расчет фехтовальщика с поэзией и вдохновением музыканта.
Но одно бесповоротно портит этот пленительный образ.
Видимо, основное личное качество Бояи — тяжелое, ревнивое, болезненное, эгоистичное честолюбие. Оно определяет все в его жизни. И оно в конце концов губит его.
Я, правда, боюсь судить безапелляционно в подобных случаях, а для оценки его работы это, естественно, вообще не имеет никакого значения, но для отношения к человеку все это важно. А Бояи, как мне кажется, был из тех людей, что подходят к себе и к остальному миру с существенно разными мерками. И потому он не очень приятен мне.
Но мне очень хотелось бы узнать, что в своей оценке я ошибаюсь.
А в истории математики место Бояи ясно. Вместе с Лобачевским он с полным правом считается творцом неевклидовой геометрии.
Правда, был еще и третий.
И здесь мы оказываемся на подступах к давней приоритетной тяжбе. Хотя подобные вопросы, на мой взгляд, не заслуживают и сотой доли того внимания, что им обычно уделяют, но история с неевклидовой геометрией исключительно интересна с чисто человеческой стороны. Только поэтому о ней стоит говорить.
Раньше всех к идеям неевклидовой геометрии пришел «геттингенский гений», «король математиков», «колосс», «титан», «первый математик мира» — Карл Фридрих Гаусс (1777–1855).
Я перечислил здесь лишь часть тех титулов, что он получил при жизни, и — ничего не скажешь — все они заслуженны.
Гаусс — личность уникального таланта. Как математик он, бесспорно, несравненно выше и Бояи и Лобачевского. Он ученый другого ранга.
Так вот Гаусс неоднократно писал, что основные идеи неевклидовой геометрии были ясны для него уже в конце XVIII столетия.
И — уверен — писал он чистую правду. Но не опубликовал своих результатов ни тогда, ни позже.
Результаты, полученные Гауссом, можно угадывать только из его писем и дневников, опубликованных после его смерти.
Почему он не публиковал эти исследования? Причина как будто известна. Он сам ее неоднократно приводит.
Вот, например, отрывок из письма к крупному немецкому математику Бесселю. Это написано уже после того, как Лобачевский напечатал свою работу. Правда, Гаусс еще не знает о ней.
«Вероятно, я еще не скоро смогу обработать свои пространные исследования по этому вопросу, чтобы их можно было опубликовать. Возможно даже, что я не решусь на это, ибо боюсь крика беотийцев, который поднимется, когда я выскажу свои воззрения».
Итак, Карл Фридрих Гаусс боялся «крика беотийцев».
Классицизмы в наше время требуют расшифровки.
Не знаю, справедливо ли, нет ли, но жители Беотии считались в древней Греции наиболее тупыми и ограниченными, а в век Гаусса и Лобачевского, век увлечения классицизмом, цитаты из античности были весьма модны.
Меня всегда не очень удовлетворяло объяснение Гаусса.
Несомненно, он называл одну из причин. Допустим даже, одну из основных. Но, бесспорно, были и другие.
Не таков был Гаусс, чтобы только из боязни рискнуть своим авторством, он умолчал бы об открытии исключительного, неповторимого значения. Тем более что он-то как раз рисковал немногим. Авторитет его в мире математиков был столь велик, что, появись мемуар Лобачевского за его подписью, все «беотийцы» признали бы и воспели неевклидову геометрию, почтительно склонившись еще раз перед гением Гаусса.
Кстати, нечто подобное и произошло. На работы Лобачевского обратили внимание только тогда, когда после смерти Гаусса выяснилось его отношение к неевклидовой геометрии. Ее идеи мгновенно стали понятны и популярны. И появись работа за подписью Гаусса — никаких сомнений бы не было.
Гаусс же, судя по всему, отнюдь не страдал непониманием или недооценкой своего положения в мире математиков. И смею думать, он понимал и то, что сможет, как истый законный король, призвать к порядку своих вассалов, коль скоро они посмеют роптать. Так что пресловутый «крик беотийцев» сам по себе вряд ли так уж безумно страшил Гаусса.
Дело в другом.
Хорош ли был Карл Фридрих Гаусс как человек или плох (биографы уже доброе столетие спорят на сей предмет), но одно бесспорно. Всю свою жизнь Гаусс отдал математике.
Математика была всем.
Решать задачи ему было столь же необходимо, как дышать, есть, пить. Это было инстинктом. Для него не существовало непривлекательных проблем.
Он мог тратить месяцы на скучнейшую, монотонную вычислительную работу, неделями заниматься составлением таблиц, с наслаждением выполнять работу, которую в наш просвещенный век поручают лаборантам; выписывать унылые столбцы цифр, которые жили, вероятно, для него своей неповторимой пленительной жизнью.
Нет, такого раздела математики, где ему не принадлежали бы крупнейшие основополагающие результаты. Простое перечисление заняло бы несколько страниц.
По складу, типу характера, по образу жизни он поразительно напоминает Исаака Ньютона, и не случайно Ньютон был любимый его герой.
И так же, как Ньютон, Гаусс исключительно честолюбив. Но это не совсем то честолюбие, что сжигало (и сожгло в конце концов) Яноша Бояи.
Прежде всего он должен сам оценить свой труд. Он сам должен быть уверен. Сам должен сказать себе: «Это хорошо, Гаусс».
И многие работы десятки лет ждут опубликования, ждут, потому что они не закончены, а дела много. Из жизни выключено всё, что может отвлечь, рассеять. Гаусс молится в храме жестокого бога, верит фанатично, и, как всякий фанатик, он ограничен.
Он жесток и суров к людям, хотя со своих позиций он справедлив. Но эта ледяная снисходительность вполне обоснованно воспринимается как безразличие, граничащее с грубостью. Он принадлежит к сложному и тяжелому типу людей. Они могут вызывать восхищение, поклонение, но любви они не вызывают никогда.
Абель, Якоби, Бояи — список блестящих математиков, жестоко обиженных Гауссом, можно значительно увеличить.
Но он вовсе не стремится обидеть. И зря пишут, что он законченный эгоист, что он страдает, когда другой получает великолепные результаты. Это неверно. Это злая клевета. Он всегда отдает дань гению собратьев. Но не его вина, что их результаты часто, очень часто совпадают с тем, что сделал он сам, но еще не опубликовал. Не опубликовал, потому что он-то знает, что еще многое надо бы сделать, что работа не завершена.
Его упрекают, зло упрекают за отзыв на работы Абеля. Почему?
Он написал: «Работы Абеля выше моих похвал, потому что они выше моих работ».
Что же, в мире думают, что он, Карл Фридрих Гаусс, просто лжет? Что он не занимался никогда сходными проблемами и не получал сходных результатов? Или «они» хотят, чтобы он разыгрывал роль благородного отца семейства? Разве мало того, что несколько десятков важнейших теорем, которые он, Гаусс, доказал, но не печатал по тем или иным причинам, опубликованы другими и славу открытия приходится делить!
И Гаусс не читает работ, присылаемых ему на отзыв, и запрещает друзьям давать ему чужие мемуары.
Он хочет так служить своему божеству, чтобы никто (а в первую очередь он сам) не мог заподозрить, что в его проповедях есть чужие фразы.
Его любовь к математике неразделима с ревностью. Это любовь мужчины. Более того — любовь мусульманина. И он жестоко переживает, если одна из его многочисленных наложниц улыбнется кому-либо другому.
Но он знает: в его гарем проникают лишь достойные. Это утешает его отчасти. И он всегда готов первый признать достоинства соперников. Но радости… Радости он не испытывает.
Так и живет внешне размеренно, покойно и однообразно этот человек. А в мозгу его непрерывно возникают и гибнут удивительные вселенные, неизмеримо более прекрасные на его вкус, чем та, где он существует.
Можно повторить: Гаусс заслуживает преклонения, но полюбить его трудно. Впрочем, не будь Архимеда и Эйнштейна, можно было бы поверить, что гениальный математик не может быть иным.
Лет сто назад, кажется, Эмерсон сказал очень любопытные слова, ставшие теперь пословицей: «Пусть каждый возьмет то, что ему хочется, и заплатит за это полной ценой».
Цена Гаусса и Ньютона была весьма высока. Эйнштейн и, насколько мы можем судить, Архимед получили все, что имели эти двое, и ухитрились избежать платы.
Человеком того же склада, что они, был и Николай Иванович Лобачевский, и хотя при всем своем блестящем таланте он ученый другого класса, чем эта четверка, он несравненно ближе и приятней мне, чем Гаусс.
Но, повторяю, я поверил бы, что Гаусс высшее существо, человек будущего или потомок мудрых марсиан, если бы не было Эйнштейна.
Одна из возлюбленных Гаусса (как трудно отвязаться от полюбившегося сравнения!) — неевклидова геометрия.
Что же не удовлетворяло Гаусса, почему он не печатал своих работ?
Мы опять вступаем на весьма скользкую стезю психологическо-детективных изысканий, но отступать уже поздно. Прежде всего, как и положено детективам, посмотрим факты.
1. Гаусс писал в частных письмах, и, безусловно, писал правду, что основные идеи неевклидовой геометрии были ясны ему еще в конце XVIII столетия. Лобачевский в это время еще не поступил в гимназию, а Бояи вообще еще не родился.
2. Исключительное значение самой проблемы очевидно. Немыслимо, чтобы Гаусс ее недооценивал.
3. Известно, мы еще вспомним об этом, что Гаусс предпринимал попытки измерить сумму углов треугольника, образованного вершинами трех гор. Следовательно, он допускал возможность, что в природе осуществляется неевклидова геометрия.
4. В архиве Гаусса после его смерти нашли лишь довольно скудные наброски; никакого сколько-нибудь систематического рассмотрения неевклидовой геометрии не было.
5. Гаусс, прочитав работы Лобачевского и Бояи, в обоих случаях подчеркивал, что, по существу, ничего нового для себя не нашел.
Здесь, правда, некоторая сложность. Дело в том, что Лобачевский несравненно шире рассматривает возможные следствия неевклидовой геометрии, чем это сделал Бояи. В этом смысле их работы несравнимы.
Лобачевский, например, довел свои исследования до стадии, когда необходимо привлечение аппарата математического анализа. Одна из его работ специально посвящена применению «воображаемой геометрии к вычислению определенных интегралов».
Во фрагментах, оставшихся после Гаусса, нет и намеков, что он добрался до подобных вопросов. Тем не менее можно думать, что Гаусс был совершенно искренен в своих письмах. Если он и не развил неевклидову геометрию столь подробно, как Лобачевский, то, вне всяких сомнений, мог бы очень легко сделать это… если бы захотел.
В принципе все «выходы» неевклидовой геометрии в анализ он, конечно, предвидел. И вероятно, без особого труда он развил бы схему неевклидовой геометрии куда глубже и подробней, потому что по гению и математической культуре равных ему не было.
Последний тезис вне сомнений.
6. Гаусс, однако, так и не придал своим идеям сколько-нибудь законченную форму и не опубликовал свои работы. Только по письмам видно, что он владел довольно многим.
Попытаемся же понять — почему?
Объяснение самого Гаусса мы отбросим. Оно примерно так же убедительно, как заявление командира линейного корабля, что он не выполнил важнейшего боевого задания, испугавшись возможной недоброжелательной реакции нескольких рыбацких лодочек, которые могли оказаться за горизонтом.
Правда, я несколько увлекаюсь. Один призрак действительно мог мерещиться Гауссу. Обвинить его в безграмотности, в бездарности, как это выпало на долю Лобачевского, не посмел бы, конечно, никто. Но вот подозрение, что Гаусс, попросту говоря, помешался, такое подозрение могло кое у кого появиться. Ибо консервативность математиков (как и вообще ученых) недооценивать нельзя.
История с неевклидовой геометрией — лучший тому пример.
Еще в семидесятые годы XIX столетия, когда уже все было ясно, когда была доказана непротиворечивость неевклидовой геометрии, когда ее идеи получили блестящее развитие, когда эти идеи были поддержаны и укреплены авторитетом всех крупнейших математиков мира, еще в эти годы многие математики-профессионалы, математики с рангом академиков предлагали все новые и новые доказательства пятого постулата и даже не желали серьезно и объективно задуматься над геометрией Лобачевского.
Кстати, одним из самых последовательных и непримиримых врагов новых идей был тот самый Буняковский, что в 1853 году совершенно игнорировал работы Лобачевского.
Но консерватизм математиков не нужно и преувеличивать.
Гаусс великолепно понимал, что передовая группа ученых, и в первую очередь молодежь, поймет и оценит новые идеи.
Да и не таков был его характер, чтобы отступать перед возможными неприятностями.
Во-первых, пожалуй, основная черта его характера — суровая, требовательная гордость, едва ли не гордыня.
А во-вторых, математику он не предавал. Ей он поклонялся с ледяной страстностью пуританина и для нее пошел бы на все. Так что никакие призраки не остановили бы его.
Второе предположение: «Гаусс не считал проблему столь уж существенной, и у него попросту «не доходили руки» до неевклидовой геометрии» — столь же нелепо.
Это означало бы, что Гаусс не более чем весьма ограниченный математик без настоящей математической культуры.
К тому же в многочисленных письмах Гаусса, где он пишет о неевклидовой геометрии, непрестанно слышишь — это проблема первого ранга; проблема центральная для математики.
Снова остро необходимы риторические вопросы.
Какова же истинная причина?
Почему же Гаусс не обратил к этой теме всю силу и энергию своего поразительного, беспрецедентного таланта? Почему он не исчерпал проблему? Почему он молчал многие годы и в итоге позволил и Лобачевскому и Бояи опередить себя?
Полагаю: доза детектива вполне достаточна, и читатели заинтригованы. Поэтому без лишних слов рассмотрим единственное мыслимое объяснение.
Начнем с некоторого напоминания. Чтобы оно было убедительно, нам необходимо четко представлять постановку всей проблемы неевклидовой геометрии.
Как помните, говоря об аксиомах, аксиоматике, мы условились, что к аксиомам любой математической теории предъявляются лишь два требования — полнота и независимость. Полнота аксиом означает, что любое мыслимое утверждение относительно первичных понятий может быть доказано с их помощью.
Аксиомы позволяют исследовать всё. Чтобы не слишком увлекаться абстрактной логикой, перейдем к конкретным примерам.
Представьте, что двое шахматистов научились игре по учебнику, где по случайности ничего не сказано о ситуации, когда один из игроков при своей очереди хода не может сделать ход, не нарушив правил. При этом его король не атакован вражеской фигурой («королю нет шаха»).
Как видите, понадобилось много слов, чтобы строго определить понятие, известное любому начинающему, — «пат».
Наши игроки окажутся в затруднении. Игру продолжить невозможно. Но чем она закончилась — неизвестно. И они просто будут обязаны ввести какое-то добавочное правило — какую-то аксиому. Если они играли до этого в шашки или «Волки и овцы», то, возможно, рассуждая по аналогии, они условятся, что в этом случае необходимо засчитывать поражение шахматисту, которому поставлен пат[5].
Но какую-то аксиому они обязаны выбрать.
Их система оказалась неполной.
Она не предусматривала все возможные ситуации.
В другой популярной игре основные понятия (объекты) — футболисты и мяч. Строго говоря, десять полевых игроков, вратарь, судья, боковые судьи, ворота, футбольное поле со всеми его линиями и мяч.
И опять же аксиомы (правила игры) должны быть составлены так, чтобы можно было однозначно судить о любой возможной ситуации для элементарных объектов.
То, что в дворовых матчах обычно не очень ясно представляют полный свод футбольного кодекса, порождает неисчислимое множество драк, что, в свою очередь, убедительно демонстрирует опасность забвения аксиоматики. Хотя, как правило, команды и договариваются перед началом игры о необходимой модификации правил применительно к условиям двора, но полная аксиоматика, даже в такой простой игре, как футбол, — дело довольно хитрое. Отсюда все трагедии.
Наконец, любой уголовный кодекс в принципе должен быть полной системой аксиом, предусматривающей все возможные опасные для общества ситуации.
Как будто намечен ясный путь проверки системы аксиом на «требование полноты».
О, если бы все было так просто, как я только что рассказывал! Математики были бы счастливы.
Позволим себе на мгновение роскошь говорить наивно.
Итак:
Система аксиом для данной группы основных (первичных) понятий полна, если для любого общего суждения А (любой теоремы), относящегося к данным первичным понятиям, мы на основе этих аксиом можем разрешить вопрос: «Истинно А или ложно?»
Теперь подумайте, что сейчас сказано. Для проверки полноты аксиом мы должны ни много ни мало как доказать или опровергнуть любую мыслимую теорему. Если это проделать, то любая математическая дисциплина будет исчерпана до конца. Исчерпана так же, как игра в «крестики-нолики».
Очевидно, наше требование нереально.
Даже в такой сравнительно простой системе, как шашки, мы не можем точно исследовать основную теорему и ответить на вопрос: каков должен быть результат партии при идеальной игре партнеров?
Тем более мы не знаем, как обстоит дело в шахматах.
И тем более мы не можем предусмотреть и проанализировать все теоремы геометрии, арифметики или вообще любой математической дисциплины.
Посему всю проблему полноты аксиом необходимо формулировать совершенно иначе.
Здесь мы не в состоянии погружаться в глубины высшей математической логики, и поэтому о проблеме полноты «во всей ее полноте» мы ничего не скажем.
Я могу лишь привести красивую и непонятную фразу: система аксиом полна, если любые две ее интерпретации, имеющие реальное содержание, изоморфны.
Причем в порядке рекламы можно добавить, что за красивыми звуками скрыт еще более красивый смысл.
Идея изоморфизма, введенная Гильбертом, одна из самых изящных находок начала XX столетия.
Но что-либо говорить об изоморфизме мы не будем.
Простой же пример, когда было ясно видно, что система аксиом неполна, уже был приведен, и вероятно, читатели без труда смогут придумать еще несколько аналогичных примеров.
Яснее на первый взгляд положение с требованием независимости (или непротиворечивости)[6].
Снова сформулируем требования независимости совершенно строго.
Пусть у нас есть какая-то группа аксиом — ? (эта буква обычно используется для обозначения суммы).
Пусть есть какое-то утверждение А.
И противоположное утверждение ?[7].
Тогда А независимо от группы аксиом ?, если ни само А, ни противоположное утверждение ? им не противоречит.
Иначе говоря, с группой аксиом ? совместимо как суждение А, так и противоположное суждение ?.
Все это очень элементарная логика. Но она, вероятно, непривычна. И потому может показаться очень сложной.
Поэтому поясним все на примере с пятым постулатом.
Мы хотим доказать его независимость от остальных аксиом геометрии Евклида («пятый постулат» сейчас — пример нашего суждения А). Мы высказываем утверждение, противоположное пятому постулату («суждение ?»). Например, мы утверждаем: через данную точку к данной прямой можно провести по крайней мере две параллельные прямые. (Для «популярности» постулат, противоположный пятому, будем записывать вверх ногами «
».)
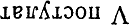Далее мы доказываем, что «
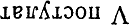» не противоречит остальным аксиомам геометрии.
Это значит, что как бы далеко и широко мы ни развили возможные следствия, мы никогда не придем к логическому противоречию.
Теперь — внимание! До сих пор все очень ясно.
Но, спрашивается, как убедиться, что мы никогда не сможем прийти к противоречию?
Пусть мы доказали двадцать непротиворечивых теорем.
Это не гарантирует нам, что противоречие не выскочит в двадцать первой.
Доказав сто, можно ожидать подвоха в сто первой…
Доказав тысячу… Короче: ясно, что на этом пути никакого строгого доказательства непротиворечивости получить нельзя. Получить же его необходимо. Без этого задача не решена. Но как будто это абсолютно безнадежная задача. Не видно даже других мыслимых путей, кроме того, что мы описывали. А наш путь заведомо и абсолютно безнадежен.
И здесь остановимся и еще раз потребуем внимания.
Во второй половине XIX века, примерно через 20 лет после смерти Лобачевского и Гаусса, был предложен строгий путь доказательства непротиворечивости неевклидовой геометрии. Путь неожиданный и невероятный.
Мы расскажем о нем позже.
Но ни Лобачевский, ни Гаусс не подозревали о возможностях такого сорта. Запомним: сама возможность принципиально новых идей, с помощью которых можно доказать непротиворечивость неевклидовой геометрии, в то время почти столь же невероятна, как возможность определения химического состава звезд.
Столь же немыслима, как опровержение механики Ньютона.
Столь же непредставляема, как термоядерная реакция.
Еще нет ясного представления об аксиоматике. Еще во всех определениях и аксиомах геометрии полный беспорядок, оставшийся в наследство от Евклида.
Почти все из того, что было написано выше, математики еще не сформулировали для себя.
Лишь гениальный Бояи нащупывает правильный путь. Но, боюсь, даже Гаусс не воспринимает полностью его идей.
Есть только полуинтуитивное представление о понятиях независимости и непротиворечивости.
Но тогда…
Тогда ясно, что логически доказать «независимость пятого постулата» вообще невозможно. Как далеко ни протянется непротиворечивая цепочка теорем, полученных при помощи «
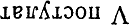», всегда останется возможность, что противоречие скрыто глубже. Останется ощущение, что мы не добрались до него.
Можно, конечно, «с отчаяния» прибегнуть к «чуждому» для математики пути — подглядеть, что дает эксперимент. Окажись, что во вселенной осуществляется «неевклидова геометрия», — вопрос о непротиворечивости отпал бы сам по себе.
Как помните, Гаусс пытался проверить, чему равна сумма углов треугольника. Независимо от него Лобачевский попросил провести подобные же измерения. У Лобачевского объект был выбран даже более удачно. По его просьбе в Казанской обсерватория измерили углы треугольника, вершинами которого были взяты три звезды. Но в обоих случаях сумма углов оказалась равной ? в пределах ошибок эксперимента.
Этот результат ничего не опровергал потому, что даже если евклидова геометрия не осуществлялась в нашем мире, отклонение от ? могло быть очень мало.
Но уж тем более он ничего не доказывал.
Итак? Итак, рассуждая строго логически, оставалось одно. Заключить, что вопрос открыт. И вероятно, останется таким навечно. В этом духе и высказался однажды Гаусс. (Разумеется, снова в частном письме.) «Я все более склоняюсь к убеждению, что необходимость нашей геометрии не может быть строго доказана. По крайней мере человеческим умом для человеческого ума».
Эту фразу можно прочесть и так. Я не представляю никакой мыслимой возможности доказать, что постулат, обратный пятому («
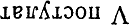»), не противоречит прочим аксиомам геометрии. И хотя интуиция, конечно, подсказывает Гауссу правильный ответ: неевклидова геометрия столь же непротиворечива, как евклидова, но доказательства нет.
Задача не решена.
Но если так, то совершенно в духе Гаусса не публиковать своих результатов. Он не может рисковать своей репутацией и печатать работу, в которой он не уверен на сто процентов. А идеи, позволяющей рассечь узел, идеи, решающей все, — такой идеи у него нет. А дальше? Дальше вступают в игру факторы, не связанные с чистой наукой непосредственно.
То один, то другой корреспондент (Швейкарт, Тауринус, Бояи) присылает ему письма, в которых более или менее явно высказывает предположение: доказать пятый постулат нельзя и противоположный постулат не противоречит остальным аксиомам Евклида.
При этом по крайней мере для Швейкарта и Тауринуса эта идея куда более смутна, куда более неуклюже оформлена, чем видит все он — Карл Фридрих Гаусс.
Представьте себя на секунду Гауссом. Не так уж просто ответить совершенно прямо и честно. Не так просто подарить свои идеи какому-то Швейкарту, полностью отказаться от затаенной надежды решить когда-нибудь эту проклятую задачу до конца, объяснить положение, посоветовать — развивайте ваши соображения как можно тщательней, как можно полней, чем больше самых разнообразных следствий и теорем вы получите, опираясь на «
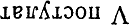», тем крепче будет внутренняя вера в его непротиворечивость. Рассмотрите неевклидову тригонометрию, попробуйте вычислять длины кривых в неевклидовой геометрии. Получите, например, выражение для длины окружности.
Гаусс-то знал, какова будет длина окружности в неевклидовой геометрии. Он приводит эту формулу в одном из своих писем.
Но наш «идеальный Гаусс», конечно, не напишет об этом своему корреспонденту.
Он вообще промолчит о своих собственных результатах. Он наметит обширную программу необходимых исследований, поддержит и ободрит младшего коллегу и заключит:
«Мне самому эта идея кажется очень привлекательной. Но, увы, сколько бы вы ни развивали ваши теоремы, в конечном счете вопрос о непротиворечивости неевклидовой геометрии — это вопрос веры. Строгое доказательство получить невозможно. Можно лишь довериться интуиции.
Вероятность ошибки всегда останется. Вы молоды. Ваше имя не канонизировано, вы можете позволить себе печатать глупости. Я настоятельно рекомендую вам посвятить все свои силы этой проблеме. Жду ваших писем».
Не правда ли, мы требуем довольно много от Гаусса?
Много. Но не слишком.
В науке были и подобные люди и подобные случаи. И фраза: «Вы достаточно молоды, чтобы позволить себе печатать глупости» — не придумана. Именно эти слова сказал замечательный человек, педагог и физик Эренфест двум молодым ребятам — Уленбеку и Гаудсмиту, когда те хотели забрать из журнала свою работу. Впоследствии эта работа и оказалась главным, что они сделали в науке. Кстати, им же совершенно бескорыстно отдал важнейшие соображения Эйнштейн, не очень заботясь о своем приоритете.
Но Гаусс не являл идеала научного бескорыстия. Хотя, и это необходимо сказать, он никогда не позволял себе некорректных поступков. Всегда был безукоризненно честен.
Впрочем, если уж судить совершенно придирчиво, — почти всегда.
Потому что в истории с неевклидовой геометрией он никогда не высказался до конца, не объяснил истинную причину, по которой не опубликовал свою работу.
И во всех письмах он настойчиво, по-детски настойчиво объясняет, как он боится несчастных шумливых «беотийцев».
Эти «беотийцы» так или иначе, как спасительные иконы, появляются почти в каждом его письме, где говорится о неевклидовой геометрии.
Я допускаю даже, что сам Гаусс в конце концов искренне поверил в собственный вымысел.
Но что это меняет? Ровно ничего.
Один из самых тонких, убедительных и распространенных видов лжи — ложь, в которую поверил сам.
Вера необходима автору, и именно она убеждает других.
Неевклидова геометрия — тоже порождение веры.
Бояи и Лобачевский поверили.
Строго говоря, в основном, решающем вопросе они мыслили как поэты, а не как поклонники строгой логики.
«Это правильно, потому что красиво» — по существу, это главный их довод.
Здесь автор испытывает настоятельную необходимость несколько порассуждать.
Только что были написаны слова «мыслили как поэты». Точнее, лучше и правильней было бы сказать: «как математики». А совсем точно: «как люди творческой мысли».
Природа творческого процесса в основных, решающих чертах едина.
Математики, физики, поэты, художники, инженеры, музыканты отличаются друг от друга значительно меньше, чем это почему-то принято считать в наш век.
Кстати, в этом вопросе древние греки думали точнее. Они почти не разграничивали природу самых разных видов творчества.
Возможно, они и впадали в некоторые преувеличения, считая, что для музыканта необходимо профессиональное изучение философии и математики. Но это преувеличение возникло на более здоровой основе, чем противоположная позиция.
Надо, правда, заметить, что резкое разграничение точных наук и искусства нельзя безоговорочно считать позицией нашего столетия. Это просто очень распространенный взгляд, причем в основном он популярен у тех, кто вообще не имеет и не имел отношения к любому виду творчества.
Объяснять этим людям природу творческого процесса, естественно, весьма трудно и тем трудней, чем солидней их официальное положение. Это столь же трудно, как объяснить поклоннику балета, что великолепный футболист не менее достоин восхищения, чем блестящая прима-балерина. Если же еще добавить, что в главном творчество нашего центра нападения и примы очень сходно, едино и по своей сути, и по цели, и по результатам, интеллигентный балетоман, вероятно, просто прекратит разговор. Впрочем, обратившись с подобными разговорами к иному футбольному болельщику, вы услышите в ответ: «Футбол не балет», плюс подтверждение этого тезиса вариациями из русского фольклора. И тем более необходимо истреблять эту унылую застывшую ограниченность, что она весьма распространена.
Успешно пофилософствовав, вернемся к геометрии. Один из главных критериев любого искусства, как известно, красота.
Через всю историю пятого постулата, начиная с Евклида и кончая Лобачевским, проходит единый стержень — стремление к красоте.
Уродливость евклидова постулата предопределила тщетные двухтысячелетние попытки доказать его.
Изящество построений неевклидовой геометрии покорило Ламберта, почти убедило Гаусса и заставило Бояи и Лобачевского сказать: это столь красиво, что имеет такое же право на жизнь, как геометрия Евклида.
В смысле веры и увлеченности первое место, вне сомнений, принадлежит Бояи. Его работа с весьма скромным названием
«Приложение,
Содержащее науку о пространстве,
Абсолютно истинную,
Не зависящую от истинности или ложности
XI аксиомы Евклида,
Что a priori никогда решено быть не может…»
написана наиболее безоговорочно.
Кстати, история забавно подшутила над Бояи с несколько пышным заглавием.
Свою работу он опубликовал как приложение к учебнику геометрии, составленному его отцом Фаркашем Бояи. Естественно, все было написано на классической латыни — языке ученых и философов. «Приложение» по-латыни — «Аппендикс». И при всем бесспорном и заслуженном уважении к Бояи, цитируя его работу, математики, как правило, сохраняют лишь первое слово заглавия «Аппендикс». Так этот труд и вошел в историю.
Чрезвычайно любопытно, быть может, даже символично, что, так сказать, «у колыбели» неевклидовой геометрии столкнулись три человеческих и научных темперамента. Три типа научного мышления.
На противоположных позициях Гаусс и Бояи.
Карл Фридрих Гаусс. Гаусс — осторожный реалист. Он, бесспорно, наиболее логичен из всех трех. Наиболее академичен. Для него задача не решена до конца, а позволить себе роскошь последовать интуиции — поверить, а не доказать — нет, этого он не может. Он все понимает и знает, при желании он, вероятно, превзошел бы и Бояи и Лобачевского. Он знает, но слишком мало верит. И он проигрывает.
Неважно, что потом будут говорить историки. Неважно, что во всех своих письмах он будет настойчиво повторять: «Я знаю это уже сорок лет». Наедине с собой Гаусс соглашается — его опередили. Более того, он достаточно честен и строг к себе, чтобы почти безоговорочно признать это. Он проиграл.
Янош Бояи. Бояи — романтик. Он покорен красотой, изяществом. Он увлечен и собственным талантом. Ведь все это сделал он, Янош Бояи. И его вера вознаграждается. Она движет его вперед. Сразу, в первой работе он понял и охватил проблему глубже всех. Впрочем, в дальнейшем он не продвинется в своих результатах. Возможно, отчасти потому, что для него все уже решено. Может быть, подсознательно, но решено.
Он добился своего. Он гений. Он доказал это.
Николай Иванович Лобачевский. Он в этой истории близок к идеалу ученого. Смешайте в равной доле научный энтузиазм Бояи и скептическую осторожность Гаусса, добавьте еще настойчивость, граничащую с упрямством, почти инстинктивную внутреннюю убежденность в безукоризненной справедливости своих идей… Потребуйте, чтобы эта научная цельность не поколебалась в результате двадцати лет полного непонимания коллег, непонимания, проявляющегося порой в прямом издевательстве, и вы получите приблизительное представление о позициях Лобачевского в деле создания неевклидовой геометрии.
Он и верил и проверял.
И вполне справедливо, что во всем мире ту неевклидову геометрию, о которой сейчас идет речь, называют геометрией Лобачевского. Ко всем этим мужам мы еще вернемся.
Снова начнем с Бояи.
Несколько раньше я написал, что Бояи не очень мне приятен, и не отказываюсь от своих слов. При этом за скобками остается тот тривиальный факт, что он математик блестящего дарования. Это он великолепно доказал, и тут говорить не о чем. Но, видимо, человек Бояи был весьма тяжелый.
Он из породы «гениев».
В каждой школе вы найдете двух-трех «ньютонов», очень способных, ярких, резко превосходящих по развитию своих сверстников, с острым и быстрым интеллектом.
И слишком часто сознание своего интеллектуального превосходства приводит юношей этого типа к некоему «ницшеанству».
Они капризны, нетерпимы, привыкают доверять лишь себе, считаться лишь со своими стремлениями, привыкают рассматривать окружающих как серую массу, толпу, удел которой вести героя на пьедестал.
Вне сомнений, порой из какого-то каприза они могут оказаться добры, отзывчивы, очень часто они одарены пленительным обаянием, но бессознательная (а позже и сознательная) их философия — философия «вождей» и «массы». Этот вариант развития одаренных ребят печален, но естествен, возможно, потому, что воспитание внутренней человеческой культуры — более длительный, сложный и тонкий процесс, чем даже раскрытие таланта. И конфликт этот между дарованием и культурой бывает тем острей и бескомпромиссней, чем раньше проявится их превосходство. Если позволено некоторое философствование, то можно думать, что, видимо, большая часть бед всего человечества связана с самодовольством — увы, почти неотъемлемой чертой подавляющего большинства людей. А если человек одарен и к его самомнению добавляется еще честолюбие, тогда либо тяжело жить ему, либо окружающим, либо, наконец, и ему и тем, кто с ним связан.
Для Бояи судьба уготовила третий вариант. Талант его проявился рано и проявился разносторонне. Он был предельно выразительным представителем того типа темперамента, который почему-то принято обозначать как «художественную», «поэтическую» натуру. Изящный, нервный, неожиданный.
Лучшая характеристика его математического таланта и интуиции то, что в 21–23 года он уже владел основами неевклидовой геометрии и, главное, видимо, твердо был убежден в полной правомочности своих идей. Узнав, что восемнадцатилетний мальчик увлекся теорией параллельных линий, его отец Фаркаш — крупный венгерский математик и, между прочим, друг по студенческим временам Гаусса — написал сыну отчаянное письмо, где патетически уговаривал его отказаться от безумной затеи.
Письмо это написано в столь экспансивном стиле, что у людей нашей эпохи может даже вызвать некоторое раздражение и сомнение в искренности автора. Примечательно оно, на мой взгляд, тем, что очень хорошо раскрывает стиль человеческих взаимоотношений в семье Бояи.
«Молю тебя, не делай только и ты попыток сделать теорию параллельных линий: ты затратишь на это все свое время, а предложения этого вы не докажете все вместе. Не пытайся одолеть теорию параллельных линий ни тем способом, который ты сообщаешь мне, ни каким-либо другим. Я изучил все пути до конца: я не встретил ни одной идеи, которой бы я не разрабатывал. Я прошел весь беспросветный мрак этой ночи, и всякий светоч, всякую радость жизни я в ней похоронил. Ради бога, молю тебя, оставь эту материю, страшись ее не меньше, нежели чувственных увлечений, потому что и она может лишить тебя всего твоего времени, здоровья, покоя, всего счастья твоей жизни. Этот беспросветный мрак может потопить тысячи ньютоновских башен. Он никогда не прояснится на земле, и никогда несчастный род человеческий не будет владеть чем-либо совершенным даже в геометрии. Эта большая и вечная рана в моей душе…»
Впрочем, Фаркаш действительно в молодости немного занимался теорией параллельных и даже пару раз посылал Гауссу «доказательства» пятого постулата. Безусловно, отец искренне беспокоился об Яноше. И странным образом при неверных предпосылках он верно предугадал конечный результат: теория параллельных действительно оказалась проклятием жизни Яноша Бояи, хотя и совсем по другим причинам, чем предполагал отец.
Когда есть дьявольское наваждение, должен присутствовать и злой дух.
Черным гением Яноша Бояи с юных лет и почти до конца дней был Гаусс.
Хотя субъективно Гаусс не виноват почти ни в чем.