Глава 3 Как предсказать непредсказуемое

Глава 3

Как предсказать непредсказуемое

Газ — это агрегатное состояние, представляющее собой тысячи миллионов молекул, которые движутся хаотично. Поскольку каждая молекула подчиняется законам Ньютона и, соответственно, уравнениям Гамильтона, можно было бы рассчитать траекторию каждой из них. Но на практике это не так. Более того, в таких вычислениях нет необходимости, потому что при наблюдении газа невозможно увидеть отдельные молекулы. Что действительно можно измерить, так это его давление, температуру и объем. Следовательно, математическая теория, описывающая изменение этих трех характеристик, смогла бы с достаточной степенью точности описать и поведение газа.

Такая теория была разработана австрийским физиком Людвигом Больцманом в конце XIX века, когда он доказал, что макроскопические характеристики газа можно вывести исходя из распределения скоростей его молекул. То есть достаточно знать процент молекул газа с каждой возможной скоростью, чтобы предсказать его поведение. Работа Больцмана была направлена на то, чтобы найти это распределение скоростей для газа в состоянии равновесия, то есть газов, макроскопические свойства которых ощутимым образом не изменяются. Ученый открыл, что скорости молекул в газе распределяются следующим образом.

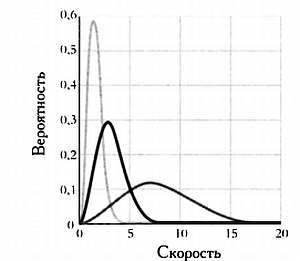
Газ с большим пиком слева соответствует большим температурам.

Чтобы сделать это, ему пришлось воспользоваться несколькими математическими теориями. Одни из них, такие как механика Гамильтона, были хорошо приняты в физическом сообществе, но другие, такие как вероятность и статистика, были совершенно новыми. Ниже мы опишем путь, который привел Больцмана к его закону и математическому обоснованию предыдущего графика.

Давление, объем и температура

Вспомним, что состояние системы в определенный момент времени может быть выражено лишь одной точкой в фазовом пространстве. Эта точка находится в пространстве из 6N измерений, где 3N используются для уточнения положения каждой из N частиц, а другие 3N — для импульсов. Если позволить системе развиваться, точка будет двигаться по фазовому пространству, описывая некоторую траекторию.

В случае с газом в самом начале мы сталкиваемся с проблемой: мы не знаем, в какой точке фазового пространства он находится. Мы знаем только его давление, объем и температуру, но не положение и не импульс его частиц. Часто мы даже не можем быть уверены в том, сколько их. Как же получить какой-либо прогноз поведения системы, о которой мы знаем так мало?

Для начала оценим наше незнание количественно: возьмем бутылку, наполненную кислородом. Если вместимость бутылки — один литр, то в ней содержится приблизительно 2,6·10²² молекул, что означает, что для того, чтобы полностью описать их состояние, нам потребуется это количество чисел, умноженное на шесть, то есть 1,6·10²³ (2,6·10²²·6 ~= 1,6·10²³). Предположим, что мы знаем температуру, объем и давление газа, то есть у нас есть три характеристики. Таким образом процент информации, которой мы владеем, в сравнении с информацией, теоретически нам необходимой, равен:

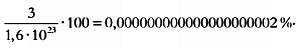
Неужели с этим смехотворным количеством информации мы можем прогнозировать состояние содержимого бутылки в каждый последующий момент? Хотя это и кажется невероятным, но это так.

Чтобы понять, каким образом мы это делаем, рассмотрим, какую информацию о внутреннем состоянии газа дают нам его давление, объем и температура.

Объем указывает нам, в какой области пространства находятся наши молекулы: нет ни одной молекулы кислорода вне бутылки, что помогает нам ограничить точки фазового пространства, в которых может находиться наш газ. Мы знаем, что возможные положения ограничены объемом сосуда. Понять роль, которую играет давление, несколько сложнее. Давление газа — это сила, которую он оказывает на сосуд, содержащий его, на единицу площади.

Представим себе, что газ — это джинн, заточенный в лампе. Чем меньше лампа и чем больше джинн борется за освобождение, тем большее давление он применяет. Чем больше давление, тем сложнее сдерживать газ; и если оно превысит определенные показатели, сосуд лопнет.

Но как связано давление с частицами, образующими газ? Если это вещество образовано огромным числом молекул, которые движутся хаотично, как объяснить эту силу, воздействующую на стенки сосуда? Давление — это результат совокупного действия миллионов молекул газа. Каждая молекула движется приблизительно по прямой до столкновения со стенкой; накопление этих столкновений и вызывает давление. Каждое столкновение воздействует на сосуд с определенной силой, и хотя удар одной молекулы не дает ощутимого эффекта, сотни миллионов молекул способны создать значительную силу.

Чем быстрее движутся молекулы, тем выше давление на стенки сосуда — по той же причине, что удар мячом по лицу тем болезненнее, чем быстрее летит мяч. Кроме того, чем больше молекул, тем большее давление они оказывают, поскольку в этом случае число ударов о стенки сосуда больше. Итак, давление дает нам информацию о движении частиц и об их числе, но в неполной форме: например, две частицы, сталкивающиеся со стенкой на одной и той же скорости, оказывают на нее такую же силу, как и две частицы на разных скоростях, если их средняя скорость равна скорости двух предыдущих частиц. Давление дает нам информацию о средней скорости частиц газа, но ничего не говорит о скорости каждой конкретной частицы.

Последняя часть информации, которой мы владеем, — это температура газа. Природа температуры была загадкой в течение веков, когда думали, что она связана с количеством флюида под названием теплород, содержащегося в веществе. Сегодня мы знаем, что температуры самой по себе не существует, то есть в фундаментальных законах Вселенной нет ничего, что было бы связано с температурой. Когда мы дотрагиваемся до очень горячего объекта, то на самом деле мы чувствуем движение частиц, его образующих. Повышенная температура соответствует быстрому движению, а низкая температура — более медленному движению. Понятие температуры можно будет определить точнее, как только мы раскроем математические инструменты, позволяющие изучать газ на основе его микроскопических характеристик. Мы можем утверждать, что температура показывает нам, как движутся молекулы. Если мы знаем температуру, объем и давление газа, то можем выяснить и сколько в нем примерно молекул и с какой средней скоростью они движутся.

* * *

ЗАКОН ИДЕАЛЬНОГО ГАЗА

Газ образован электрически заряженными молекулами разнообразных форм, и именно по этой причине так сложно предсказать их поведение. К счастью, при высоких температурах и низких давлениях эти молекулы ведут себя практически как идеально круглые мячи, которые взаимодействуют только при столкновении друг с другом. Газ, образованный таким типом частиц, называется идеальным газом, и его поведение можно описать простым уравнением.

Уже в XVII веке открыли, что произведение давления на объем газа остается постоянным при постоянной температуре. Также было известно, что повышение температуры влечет за собой повышение давления при постоянном объеме или увеличение объема при постоянном давлении. Количество газа также имеет значение: чем больше молекул, тем больше давление, так как число столкновений со стенками сосуда растет.

Все эти открытия можно свести воедино в известном законе идеального газа. В формуле ниже Р обозначает давление, V — объем, Т — температуру, R — газовую постоянную, а n — это величина, связанная с числом молекул:

PV = nRT.

С помощью этого простого уравнения можно объяснить большую часть свойств газов, которые мы наблюдаем.

* * *

Объемы в фазовом пространстве

Зная объем, температуру и давление газа, мы не можем знать, в какой части фазового пространства он находится, но можем ограничить область, в которой микроскопические свойства порождают макроскопические, которые мы и наблюдаем. Для этого сначала рассмотрим две частицы, чтобы затем расширить наш метод на сколь угодно большое их число. Также ограничимся только одним измерением, то есть предположим, что частицы движутся стихийно из стороны в сторону по прямой, что позволит увидеть их положения в фазовом пространстве.

Предположим, что наши частицы ограничены областью пространства длиной в один метр, то есть представим, что газ находится в коробке объемом в один кубический метр. Вне этой области частицы находиться не могут. Если мы обозначим через q₁ положение первой частицы и через q₂ — положение второй, их общее положение в фазовом пространстве будет ограничено квадратом со стороной в метр, как показано на рисунке.

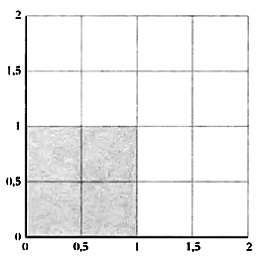
То есть ни частица 1, ни частица 2 не могут выйти за пределы области, их ограничивающей.

Поскольку мы знаем температуру и давление частиц, мы также знаем, чему равна их средняя скорость. Чтобы вычислить ее, сложим скорость обеих частиц и разделим ее на два. Выражаясь математически, если v? обозначает среднюю скорость, v₁ — скорость первой частицы, a v₂ — скорость второй, получается, что:

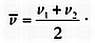
Для N частиц мы бы сложили скорости их всех и разделили на N, то есть

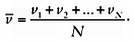
Мы считаем, что все скорости положительны и все частицы движутся в одном направлении. Теперь предположим, что средняя скорость обеих частиц — 2 м/с. Может быть так, что обе движутся со скоростью 2 м/с; что одна движется со скоростью 3 м/с, а другая — 1 м/с; что одна абсолютно неподвижна, а другая движется со скоростью 4 м/с. Единственный невозможный вариант — так это чтобы какая-либо из двух частиц двигалась со скоростью больше 4 м/с, поскольку тогда средняя скорость была бы больше 2.

Можно сделать вывод, что если известна средняя скорость, область в фазовом пространстве, в которой может двигаться система, снова ограничена. В этом случае скорость любой из частиц не может быть больше четырех; кроме того, скорость одной из частиц определяет скорость другой. Это можно представить следующим образом (скорость первой частицы представлена горизонтально, скорость второй — вертикально).

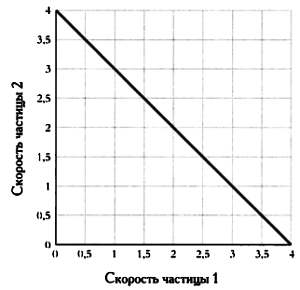
Как можно заметить, возможные точки ограничены прямой линией. Если мы совместим этот результат с полученным ранее, то увидим, что все возможные точки ограничены некоторой областью фазового пространства, которое в этом случае имеет четыре измерения, по два для каждой частицы.

Описанная ситуация справедлива для любого числа частиц. Объем, температура и давление определяют, в какой области фазового пространства находится газ. Любая из точек этой области порождает значения для характеристик газа — давления, объема и температуры. Итак, при изучении газа мы можем предположить, что наша система начинается в одной из этих точек, но не можем выяснить, в какой именно.

Что произойдет, если мы позволим системе меняться? Останутся ли температура, объем и давление теми же? И если нет, то как они будут меняться? На эти вопросы можно ответить не всегда. Порой попытка найти ответ заставляет обратиться к физике неравновесных систем, о которой мы расскажем в следующей главе.

Понятие совокупности

Поскольку мы не способны определить даже начальное положение нашего газа в фазовом пространстве, нам нужна стратегия, которая позволила бы нам описать его изменение на основании трех величин, которые мы можем измерить: давления, объема и температуры. Для этого мы можем задать вопрос, что происходит со всеми системами, которые находятся в ограниченной области фазового пространства с указанными характеристиками. Кажется нелогичным считать, что описать изменение тысяч миллионов систем легче, чем сделать это для одной. Но здесь в игру вступают теория вероятностей и статистика.

Возьмем груз, привязанный к пружине, как показано на рисунке.

Если мы знаем общую энергию частицы и область в пространстве, в которой она находится, можно выяснить, какие точки в фазовом пространстве совместимы с этими условиями. В нашем случае они распределяются таким образом.

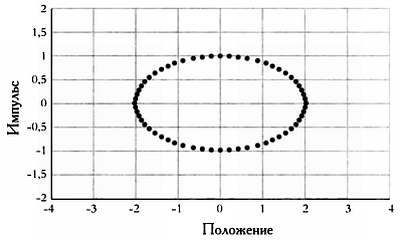
Точки фазового пространства для объекта, привязанного к пружине.

Результат вполне логичен, поскольку траектория частицы в фазовом пространстве — это именно эллипс, как мы видели в главе 2. Если мы позволим нашей системе меняться, она пройдет через все возможные точки в фазовом пространстве, совместимые с этой средней скоростью и энергией.

В целом множество точек в пространстве, совместимых с некоторой температурой, давлением и объемом, будет иметь подобный вид, хоть и в пространстве с большим количеством измерений.

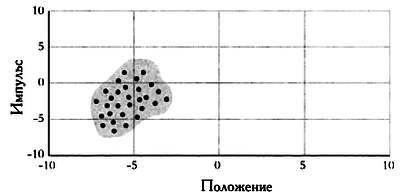
Возможные точки в фазовом пространстве. Любая из них может представлять газ.

Наша система могла бы быть представлена любой из этих точек. Возможно, что при изменении состояния газ пройдет через них, и мы этого не осознаем, поскольку способны измерить только макроскопические величины. Таким образом, имеет смысл изучать поведение каждой системы в рамках интересующей нас области.

Множество систем, совместимых с макроскопическими переменными, которые мы измерили, называется совокупностью. Следующие параграфы посвящены изучению изменения нашей совокупности, которая является не чем иным, как всеми системами, которые могли бы порождаться измеряемыми величинами.

Газ в состоянии равновесия

Мы увидели, что невозможно узнать положение и импульс каждой молекулы газа. Однако можно узнать распределение импульсов и скоростей. То есть мы можем знать, какая доля частиц находится в данном месте и движется с определенной скоростью.

Найти распределение импульсов и положений — довольно сложная задача. Однако ее можно облегчить, если мы сосредоточимся на равновесных системах. Равновесие, если речь идет о газах, немного отличается от равновесия в обычно понимаемом виде. Мы говорим, что частица пришла в равновесие, когда она перестает двигаться или движется с постоянной скоростью, и это означает, что на нее не воздействует какая-либо сила. В случае с газами их частицы продолжают двигаться под воздействием силы, которую на них оказывают стенки сосуда. Однако мы можем говорить о состоянии равновесия: если мы позволим нашей системе развиваться в течение бесконечного времени, наступит момент, когда макроскопические изменения больше не будут наблюдаться. Тогда мы скажем, что наступило равновесие. Газ придет в равновесие, когда прекратится обмен энергией и материей с внешним миром.

Заметьте: это не значит, что система не развивается. Поскольку молекулы движутся постоянно, частицы газа описывают траекторию в фазовом пространстве. Но эта траектория не приведет к макроскопическому состоянию, несовместимому с общей энергией, которой обладает газ, поскольку нет притока энергии извне.

Итак, траектория частиц ограничена некоторой областью в фазовом пространстве. Мы хотим увидеть, можно ли сделать какой-то вывод о движении газа в состоянии равновесия по области фазового пространства, которой он ограничен. Вначале мы должны убедиться в том, что как бы ни менялось состояние, газ никогда не выйдет за пределы этой области, поскольку это будет означать, что газ вышел из состояния равновесия.

Обратим внимание на точки границы нашей области в фазовом пространстве. Эти точки представляют собой границу нашей системы: если бы наш газ находился вне их, мы могли бы замерить изменение одной из макроскопических переменных, которые мы контролируем. Теперь возьмем точку из середины, как показано на рисунке.

Возможно ли развитие системы таким образом, чтобы эта точка оказалась вне нашей области?

Предположим, что точка внутри области может двигаться по траектории, которая вывела ее за границу. Это означало бы, что в какой-то момент траектория, пройденная точкой на границе, и наша система пересеклись бы. Но в предыдущей главе мы видели, что это невозможно: классическая физика основана на идее о том, что в каждый момент времени Вселенная меняется по определенным законам, и эти законы не предполагают больше одного варианта развития событий, иначе это привело бы к непредсказуемости мира. Значит, две одинаковые точки должны двигаться сходным образом. Следовательно, точка внутри никогда не сможет пересечь контур, и все точки внутри области останутся в ней. А поскольку никакая внешняя система не может войти в область и никакая внутренняя не может выйти, число систем нашей области должно оставаться постоянным.

Из этого рассуждения есть и другое следствие, которое автоматически применяется при рассмотрении газа в состоянии равновесия: область, которую занимает множество наших систем в пространстве, никогда не меняется. Пользуясь уравнениями Гамильтона, можно доказать, что это справедливо для любой совокупности, независимо от того, находится ли она в равновесии. То есть:

— количество систем в совокупности всегда одинаково;

— область, которую занимает совокупность в фазовом пространстве, всегда одинакова.

Если рассматривать точки нашей совокупности, как будто это частицы, движущиеся по пространству из многих измерений, это означает, что они ведут себя как несжимаемый флюид: траектории никогда не пересекаются, и невозможно сжать область, которую занимает одна из них. Этот вывод известен как теорема Лиувилля.

Теперь у нас есть почти все необходимые элементы, чтобы спрогнозировать распределение скоростей в газе. С одной стороны, мы знаем, что область, которую занимает наша совокупность в фазовом пространстве, не изменится; с другой стороны, если газ находится внутри границы, он останется внутри нее.

Нам не хватает только одной детали, которую необходимо ввести вручную, поскольку она не следует из уравнений Гамильтона. Вспомним, что состояние газа представлено точкой на фазовой диаграмме и что эта точка постепенно движется, описывая траекторию в рамках границы, которая очерчивает нашу совокупность.

Выдвинем гипотезу о том, что газ в конце концов пройдет по всем точкам фазового пространства, или, другими словами, что у всех этих точек одинаковая вероятность быть занятыми. Этот принцип называется принципом равновероятности начальных состояний. Теперь у нас действительно достаточно условий для вычисления распределения скоростей и положений газа. Осталось только изложить теорию вероятностей.

Теория вероятностей

Предположим, что мы хотим спрогнозировать, что будет делать какой-то человек в воскресенье вечером. Как бы хорошо мы его ни знали, нам сложно угадать: люди иногда меняют свое мнение внезапно, и это придает их поведению некоторую хаотичность. Даже человек, который привык ходить в кино каждое воскресенье, однажды может проснуться с болью в желудке и остаться дома.

Учитывая сложность, которая таится в прогнозировании поведения человека, резонно предположить, что предсказать поведение миллионов людей еще сложнее. Но в действительности оказывается наоборот: каждый человек непредсказуем, но миллион людей ведут себя известным образом. Мы не можем знать, пойдет ли наш друг смотреть фильм в это воскресенье, но можем быть уверены, что определенный процент населения это сделает. Если нас интересует прогноз, сколько заработает кинотеатр в течение года, у нас более чем достаточно информации.

То же самое происходит с переменными, еще более хаотичными, чем человек, такими как результат броска игрального кубика. Невозможно узнать, получим ли мы при следующем броске три, но мы можем быть почти уверены, что на каждый миллион бросков количество выпавших троек составит одну шестую. Если бы результат многочисленных бросков был таким же непредсказуемым, как и одного, казино давно разорились бы.

Идея о том, что миллион человек более предсказуем, чем три, делает возможным и изучение газов. Именно тот факт, что число его молекул огромно, превращает газ в крайне регулярный объект, и мы можем использовать для прогнозирования теорию вероятностей. Хотя мы и не можем знать, как поведет себя каждая отдельная молекула, в случаях когда речь идет об огромном их числе, неизвестность уступает место предсказуемому поведению.

Вероятность и газ

Прежде чем сосредоточиться на поведении газа в состоянии равновесия, рассмотрим наиболее простые примеры теории вероятностей для разработки необходимого математического аппарата. Начнем с классического подбрасывания монеты, чтобы затем расширить эту модель на газ с частицами, обладающими разной энергией.

Предположим, что мы подбрасываем монетку в воздух больше миллиона раз. Мы знаем, что, согласно теории вероятностей и здравому смыслу, мы получим в половине случаев орла и в половине — решку. Вероятность какого-то события измеряется отношением к единице, то есть вероятность в 50 % выражается как 0,5. Итак, вероятность получить орла — 0,5. Поскольку вероятность получить решку также 0,5, можно заметить, что вероятность получить либо орла, либо решку равна единице, то есть 100 %. Это общий закон вероятностей: если даны все возможные результаты, сумма вероятностей их получения должна быть равна единице.

Вероятность получения орла относительно легко вывести: это 50 %. Но как мы можем узнать вероятность получения за три броска двух орлов и одной решки?

Рациональная стратегия состоит в том, чтобы сосчитать все вероятности, возможные при этой комбинации, и поделить полученное число на общее количество возможных бросков. Если обозначить через 1 орла и через 0 решку, мы увидим, что возможны три сочетания, дающие два орла и решку:

110, 101, 011.

Для того чтобы вычислить вероятность, мы должны узнать общее количество возможных последовательностей, а именно:

111, 110, 101, 100, 011, 010, 001, 000,

то есть у нас есть восемь вариантов, три из которых соответствуют нужной последовательности. Вероятность получения двух орлов и одной решки равна 3/8.

Однако газ состоит не из трех, а из миллиардов частиц. Следуя аналогии с монетами, какова вероятность получить ровно 70 % орлов при двух миллионах бросков? В этом случае становится очевидным, что наш метод вычисления вероятностей не годится, и нам нужно разработать более мощный математический аппарат, который позволил бы нам легко рассчитать вероятность некоторого распределения результатов для любого количества бросков, то есть распределение вероятностей.

Как мы увидим, существуют различные варианты распределения вероятностей, и каждый из них имеет место в каждом отдельном случае. В данном случае нас интересует, что происходит с дискретной переменной — это означает, что мы имеем дело с отдельными результатами, такими как орел или решка. Существует другой тип переменных, называемых непрерывными, под которыми подразумевается любая величина в некотором диапазоне: например от 0 до 10, включая любое число с произвольным количеством знаков после запятой.

Для наших рассуждений важно знать факториальную функцию. Факториал 3 обозначается 3! и вычисляется следующим образом:

3! = 3·2·1.

5! = 5·4·3·2·1.

Факториал п вычисляется следующим образом:

n! = n·(n — 1)·(n — 2)·…·2·1.

Теперь мы можем начать выводить формулу, которая даст нам вероятность получения некоторой последовательности орлов и решек при любом количестве бросков.

Для начала посмотрим, сколько возможных комбинаций выпадения орла и решки существует для n бросков. Для первого броска возможны два варианта: орел или решка. Для второго — еще два, что в сумме дает четыре. Для следующего броска у нас есть по две возможности для каждого предыдущего, что в сумме дает восемь. Итак, общее число возможностей для n бросков равно 2ⁿ, то есть два, умноженное само на себя n раз.

Далее нам нужно вычислить количество комбинаций, при которых можно получить k орлов при n бросков. Подставляя различные числа, можно выяснить, что количество комбинаций задано биномиальным коэффициентом, который определяется по следующей формуле с использованием факториальной функции:

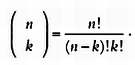
Вероятность выпадения k сторон, следовательно, равна 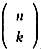разделенному на число комбинаций орлов и решек, которое, напомним, равно 2ⁿ. Поскольку в этом распределении вероятностей используется биномиальный коэффициент, оно известно как биномиальное распределение и может быть легко расширено на фальшивые монеты, где вероятность выпадения решки больше, чем орла, или наоборот.

Биномиальное распределение позволяет сделать прогнозы, которые, как кажется, противоречат здравому смыслу. Например, какова вероятность выпадения 50 орлов за 100 бросков? Применим нашу формулу, помня, что вероятность — это отношение к единице, а не к 100:

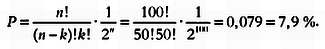
Этот результат может показаться удивительным, мы ведь ожидали 50 орлов на 100 бросков. Почему же вероятность получилась такой низкой? Ответ в том, что мы интересуемся вероятностью выпадения именно 50 орлов. Теперь найдем вероятность выпадения сорока девяти:

* * *

ПАРАДОКС МОНТИ ХОЛЛА

Парадокс Монти Холла — это применение теории вероятностей, противоречащее обычной интуиции. Представьте конкурс, когда игроку предлагается на выбор три двери, за одной из которых — ценный приз.

Конкурс состоит из двух частей: в первой части конкурсант выбирает дверь, но не открывает ее. При этом ведущий открывает одну из двух оставшихся дверей и показывает, что приза за ней нет. Во второй части конкурсант должен или сохранить свой первоначальный выбор, или изменить его на ту дверь, которую осталось открыть.

Большинство людей считают, что изменение выбора не имеет значения: вероятность того, что игрок выбрал правильную дверь, 50 %, поскольку есть две двери и приз. Однако это не так: лучшая стратегия — изменить выбор.

Объяснить это можно следующим образом: вероятность выбора правильной двери составляет одну треть. И после того, как ведущий убрал один из вариантов, вероятность того, что игрок выбрал правильную дверь, не изменилась: она по-прежнему равна одной трети. Но вероятность того, что приз за оставшейся дверью — 66 %.

Хотя люди считают эту проблему очень сложной, недавние эксперименты с голубями показали, что у этих птиц статистические способности выше, чем у нас, потому что после нескольких попыток они всегда выбирают смену двери.

* * *

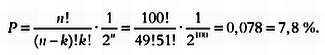
Полученное число несколько меньше, но относительно высоко. Получаем, что вероятность выпадения 48 орлов равна 7,3 %. Следовательно, вероятность выпадения числа орлов между 48 и 52 равна:

Р = Р₄₈ + Р₄₉ + Р₅₀ + Р₅₁ + Р₅₂ = Р₅₀ + 2Р₄₉ + 2Р₄₈ = 7,9 + 2·7,8 + 2·7,3 = 38,1 %.

Распределение вероятностей максимально для 50 орлов и уменьшается по мере того, как мы отдаляемся от центра, что и показано на графике.

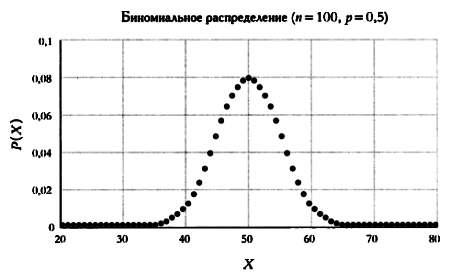
Биномиальное распределение для различного числа бросков (n) и вероятности получения орла (р).

Итак, хотя вероятность выпадения ровно 50 орлов невысока, мы можем быть достаточно уверены в том, что получим от 45 до 55 орлов. Этот способ рассуждения используется при проведении социальных опросов.

Предположим, что 50 % жителей страны проголосуют за определенного кандидата. Если мы проведем опрос тысячи людей, выбранных случайно, крайне маловероятно, что ровно 500 из них ответят, что проголосуют за этого кандидата. Однако гораздо более вероятно, что таким будет ответ от 450 до 550 опрошенных. Способ увериться в том, что опрос достоверный, — установить, между какими двумя величинами заключено 95 % вероятности получить необходимый результат.

Биномиальное распределение — это только одно из многочисленных дискретных распределений вероятностей. Кроме него, существует распределение вероятностей для непрерывных переменных, при котором нас интересует вероятность того, что какое-то значение находится в определенном диапазоне.

Самое известное непрерывное распределение вероятности — это распределение Гаусса, или нормальное распределение. Оно имеет форму колокола, как можно заметить на графике на стр. 74.

* * *

ДРУГИЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ

Другое широко используемое распределение — это геометрическое распределение. Как и в случае с биномиальным распределением, у нас есть случайное событие, такое как бросок кубика или монеты. Назовем успехом один из возможных вариантов, например выпадение орла. Какова вероятность того, что первый успех появится после к бросков, если его вероятность равна р?

Геометрическое распределение говорит, что эта вероятность вычисляется по

Р = (1 — р)^k-1р,

что можно представить следующим образом.

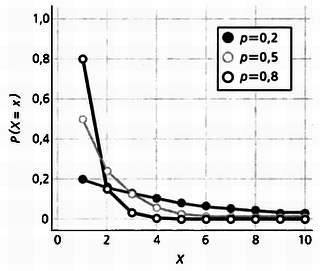
Среди распределений вероятности, где переменная может принимать любое значение в определенном диапазоне, самое простое — равномерное распределение, при котором каждому событию просто назначается одна и та же вероятность, так что получается фигура, подобная этой.

* * *

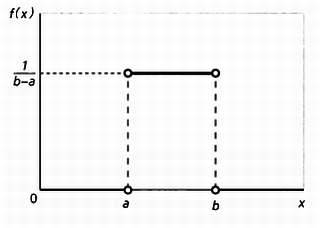
Различные формы нормального распределения, согласно разным параметрам.

Нормальное распределение имеет большое значение как в статистике, так и в естественных и социальных науках, благодаря центральной предельной теореме. В ней говорится, что в некоторых условиях любая случайная переменная имеет тенденцию следовать нормальному распределению. Например, если мы будем измерять такую физическую величину, как скорость, наши результаты будут иметь тенденцию распределяться согласно фигуре, изображенной на графике, вокруг среднего значения. Именно использование этого распределения позволяет физикам определить границы доверия своим экспериментам: измерив площадь под кривой Гаусса, можно получить вероятность того, что результат измерения случаен.

Нормальное распределение можно наблюдать практически во всех областях знания, и оно имеет очень широкое практическое применение. Например, результаты любого экзамена имеют тенденцию следовать нормальному распределению вокруг средней оценки. Этот фактор можно использовать при вычислении нормализованных оценок, то есть оценка каждого студента определяется в зависимости от положения на кривой. Распределение скоростей молекул газа также следует этому распределению, как будет показано далее.

Нормальное распределение связано с биномиальным распределением, о котором мы говорили ранее. При очень большом числе попыток биномиальное распределение описывает кривую Гаусса.

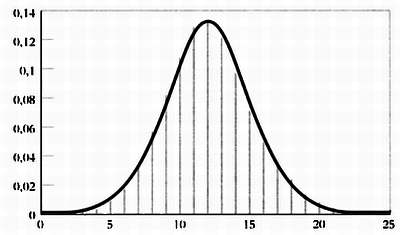
Связь между биномиальным и нормальным распределениями. Прямые показывают биномиальное распределение, вокруг которого проходит нормальное распределение.

Действительно, для получения знаменитого распределения вероятностей для газа Больцман начал рассматривать дискретные значения энергии как биномиальную функцию и затем перешел к бесконечно большому их числу, что привело его к распределению Гаусса.

Микро- и макросостояния

Познакомившись с теорией вероятностей, пора применить полученные знания к описанию газа. Для этого нам потребуются такие понятия, как микросостояния и макросостояния.

Предположим, что у нас есть газ, обладающий некоторым давлением, объемом и температурой. Нам известны макроскопические характеристики газа, но мы не знаем, под каким давлением находится каждая его молекула и с какой скоростью она движется. Итак, можно сказать, что мы знаем макроскопическое состояние газа, но не микроскопическое. Это макроскопическое состояние газа называется макросостоянием.

Макросостоянию могут соответствовать тысячи миллионов микроскопических состояний: например, поменяв положение и скорость любой пары частиц, мы получаем систему, на первый взгляд, с теми же свойствами. Поскольку у нас тысячи миллионов частиц, существует огромное количество микроскопических состояний, согласующихся с тем, что мы наблюдаем в лаборатории. Эти микроскопические состояния, которых невозможно добиться экспериментально, называются микросостояниями. Каждому макросостоянию в целом соответствуют тысячи миллионов микросостояний, которые порождают одно и то же поведение в крупном масштабе.

Теперь обратим внимание на газ, обладающий некоторым количеством возможных макросостояний, каждому из которых соответствуют некоторое давление, температура и объем. Мы хотим узнать, в каком из этих макросостояний находится газ. Поскольку макроскопические характеристики газа связаны с распределением скоростей его молекул, на самом деле мы хотим узнать это распределение.

Как мы видели, для этого мы не можем воспользоваться уравнениями Гамильтона, но зато мы можем использовать различные результаты, полученные ранее: например, то, что, перейдя в состояние равновесия, газ не выйдет из него и что все микроскопические конфигурации — или микросостояния — в нашей области фазового пространства равновероятны.

Поскольку все микросостояния равновероятны, разумно предположить, что макросостояние с наибольшим числом совместимых микросостояний будет наиболее вероятным. Если вероятность некоторого макросостояния намного выше, чем у любого другого, мы можем сделать вывод, что газ находится в нем. То есть наше макросостояние будет тем, для которого распределение скоростей наиболее вероятно.

Теперь нам осталось только выяснить, какое из возможных распределений скоростей имеет самую высокую вероятность.

Чтобы рассмотреть возможные состояния, нам нужно сделать небольшое упрощение: предположим, что все молекулы могут обладать только определенными значениями энергии, а не любыми в некотором диапазоне. Как только мы получим интересующее нас выражение, мы ослабим это условие. Энергии и скорости пропорциональны, так что, узнав распределение энергии, мы получим распределение скоростей.

Присвоим число каждому из этих значений энергии, от одного до k. У нас всего N частиц; число частиц с энергией i будет обозначаться N_i. То есть если у нас есть 50 частиц первого уровня энергии, то N₁ = 50. Теперь предположим, что у нас есть некоторое распределение энергии.

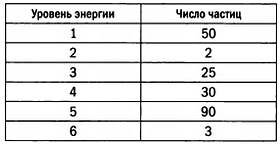
Мы хотим узнать, сколько комбинаций частиц дает нам именно это распределение. У нас всего 200 частиц, из которых 50 находятся на первом уровне энергии.

Пронумеруем наши частицы от одного до 200. Сколько существует возможных комбинаций, при которых на этом уровне находятся 20 частиц? Чтобы выяснить это, воспользуемся стратегией, очень похожей на ту, что мы применяли с биномиальным распределением.

Для первой частицы у нас есть 200 возможностей — столько, сколько у нас частиц. Для второй — 199, поскольку первая уже выбрана; для третьей — 198, и так далее. В итоге у нас получится:

200·199·198·197·…·151 возможностей.

Нам нужно разделить общее число возможных комбинаций между 50 частицами, которыми мы располагаем, так же как мы это делали с выпадением орла или решки. Так как у нас 50 частиц, получаем 50·49·…·1 возможностей. Число возможностей равно:

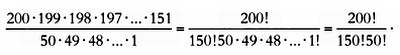
Если мы повторим эту операцию для каждого значения энергии, то получим число конфигураций, совместимых с нашим распределением. Больцман доказал, что это число можно вычислить, пользуясь факториальными функциями:

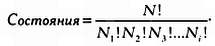
С этим уравнением очень сложно работать, так как оно содержит факториальные функции, которые, при больших значениях N, дают в результате огромные числа. Однако мы можем примерно понять возможные прогнозы.

У нашего газа есть заданная энергия. Так как она ограничена с внешней стороны, суммарная энергия не может измениться. Если бы у нас было много частиц с очень большой энергией, нам пришлось бы выбрать много частиц с небольшой энергией, чтобы компенсировать это. Поскольку количество энергии ограничено, число частиц с большой энергией также ограничено. Мы можем сделать вывод, что существует мало комбинаций, при которых у большого количества частиц очень большая энергия. Точно так же, если бы у большого количества частиц была очень небольшая энергия, нам пришлось бы выбрать много частиц с большой энергией, чтобы компенсировать это. Это означает, что сокращается число вариантов и, следовательно, существует мало комбинаций со значительным числом частиц с очень большой или очень небольшой энергией.

* * *

ВЫВЕДЕНИЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ БОЛЬЦМАНА

Распределение вероятности Больцмана можно получить после серии операций с факториалами. Предположим, что у нас есть N₁ частиц с энергией первого уровня, N₂ — с энергией второго уровня, и так далее. Нас интересует число возможных комбинаций для помещения N₁ частиц в N мест. Для первой частицы у нас есть N вариантов, для второй (N — 1), и так далее до (N — (N₁ — 1)). Это дает нам следующее количество состояний:

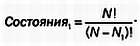
Поскольку нам не важен порядок, в котором мы расположим N₁ частиц, мы должны разделить это на все их возможные комбинации, а именно на N₁!. Получаем:

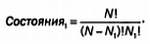
Если мы осуществим ту же операцию для второго уровня, то получим похожую формулу, хотя в этом конкретном случае вместо N начальных возможностей у нас будет только (N — N₁):

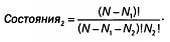
Мы можем применить это рассуждение ко всем энергетическим уровням. Общее число комбинаций будет результатом их умножения:

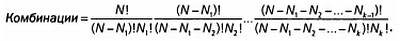
Далее видим, что большинство членов сокращается и остается выражение:

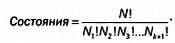
Это распределение вероятностей и вывел Больцман.

* * *

Зато если большинство частиц имеют энергию, приближенную к средней, у нас есть много вариантов для выбора. Следовательно, наиболее вероятная комбинация значений энергии — та, в которой большинство частиц имеет энергию, приближенную к средней, и только энергия некоторых сильно отличается от средней. Поскольку энергия и скорость частицы связаны, мы можем сделать тот же вывод о скоростях.

Из предыдущего рассуждения следует, что распределение скоростей молекул газа имеет форму, похожую на ту, что показана на графике на стр. 57.

Как видно из этого графика, пик скоростей находится вокруг наиболее вероятной скорости, и чем больше мы отдаляемся от него, тем сложнее найти частицу с такой скоростью. Результат совпадает с тем, что нам говорит здравый смысл. Представим себе, что у нас есть частица, которая движется очень быстро; рано или поздно она столкнется с другой и передаст ей часть своей энергии, после чего замедлится. Если частица движется очень медленно, рано или поздно она столкнется с другой, более быстрой, и ее скорость увеличится. А частица, движущаяся со средней скоростью, скорее столкнется с частицами, движущимися с той же скоростью, и, следовательно, она не приобретет и не потеряет энергию.

Хотя распределение скоростей, которое мы видели выше, было предложено Джеймсом Клерком Максвеллом (1831–1879), именно Больцман подвел под его идеи теоретическое обоснование, поэтому его называют распределением Максвелла — Больцмана. В его математическом выражении используется экспоненциальная функция у основанная на числе Эйлера, е. Число е — это иррациональное число, приблизительно равное 2,71828. Вычисляется оно сложением следующего бесконечного ряда:

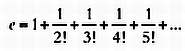
Точно так же как 2³ — это 2·2·2, е можно возвести в любую степень: е³  = = е·е·е. Распределение Максвелла — Больцмана выражается с помощью экспоненциальной функции следующим образом:

где m — масса молекул газа, k — постоянная Больцмана, Т — температура газа и v — скорость молекулы. Экспонента быстро растет при росте v — поскольку 2¹⁰ намного больше, чем 2². Это означает, что вероятность найти молекулы с очень высокими скоростями должна быть очень маленькой. С другой стороны, когда v равна нулю, вероятность равна ему же, и это означает, что невозможно найти молекулу, которая находилась бы в состоянии покоя.

* * *

ЧИСЛО ЭЙЛЕРА

Число Эйлера — одно из самых важных в математике. Кроме того, что это иррациональное число, у него есть ряд поистине волшебных свойств. Возможно, самое интересное из них то, что экспоненциальная функция, е^x равна своему угловому коэффициенту. Возьмем следующий график.

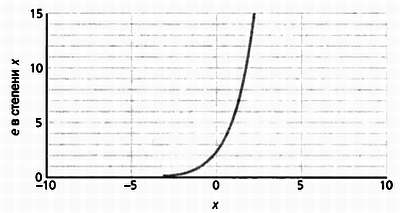
Угловой коэффициент функции — это точка, которая определяется как отношение между возрастанием функции по высоте и возрастанием по горизонтали. На этом графике мы можем вычислить угловой коэффициент в каждой точке. Итак, если мы представим угловой коэффициент функции х, то получим тот же график.

Число Эйлера связано и с другим известным числом, ?. Существует уравнение, связывающее е с ? и мнимой единицей i, которая определяется как квадратный корень из -1:

e^i? - 1 = 0

Многие математики считают это уравнение одним из самых элегантных в истории науки, поскольку в нем самые важные числа собраны в простом тождестве.

* * *

Другие виды статистики

До сих пор мы считали, что частицы газа подобны бильярдным шарам. Даже если они очень похожи, мы можем каким-то образом различить их. Например, мы можем снять их на видео и следить за их изменением или пометить их фломастером. Однако это предположение, которое, кажется, соответствует здравому смыслу, не работает для очень маленьких частиц, таких как атомы или молекулы. Не существует способа отличить два атома водорода, дело выглядит так, будто это одна и та же частица, которая одновременно находится в двух разных местах. Это справедливо для любой элементарной частицы — электрона, протона или фотона.

Указанная тонкость не имеет значения при анализе свойств газа комнатной температуры, но становится очень важной в изучении газовой динамики при низких температурах и высокой плотности. В этой ситуации распределение Максвелла — Больцмана дает ошибочный результат для распределения скоростей молекул.

Этот факт обязал физику полностью трансформировать математическую теорию, которая использовалась для описания объекта, образованного из нескольких частиц, благодаря чему были созданы новые типы статистики: статистика Бозе — Эйнштейна и статистика Ферми — Дирака, которые мы рассмотрим позже. Несмотря на то что основание этих дисциплин лежит в области физики, они могут считаться математическими инструментами.

Предположим, что у нас есть газ, состоящий из нескольких молекул. Возьмем две из них и заменим одну на другую. Изменилось ли при этом состояние газа?

Классическая физика утверждает, что изменилось: хотя обе частицы на практике неразличимы, им можно, например, дать имена — «Андрей» и «Филипп». В первом случае Андрей стоит слева, а Филипп справа, а во втором случае — наоборот. А поскольку микросостояние изменилось, то и целая вселенная, в которой Андрея и Филиппа поменяли местами, совсем не та же самая, что была до этой перемены.

Квантовая механика, то есть теория, описывающая микроскопический мир, дает другой ответ. Единственное, что нам важно во время изучения частицы, это ее степени свободы — числа, нужные для описания ее состояния. Например, состояние молекулы задано ее импульсом, положением и вращением вокруг своей оси. Если мы заменим ее на идентичную молекулу с тем же импульсом, положением и вращением, не существует способов различить эти частицы. Поскольку все получение информации о Вселенной сводится к замерам, обе частицы — на самом деле одна и та же. Даже в теории между ними невозможно найти различия.

Есть и еще одна важная тонкость. В квантовой механике известно два типа частиц: бозоны и фермионы, которые отличаются типом вращения вокруг своей оси. Оказывается, что эти частицы имеют совершенно разные статистические свойства: два бозона могут быть одновременно в одном и том же состоянии, в то время как два фермиона — нет. Из-за этого макроскопическое поведение субстанций, образованных бозонами либо фермионами, абсолютно различно.

Когда мы говорим, что два бозона могут находиться в одном и том же состоянии, мы имеем в виду, что, например, у нас может быть два фотона в одном и том же месте с одинаковой энергией. Это справедливо не только для фотонов, но и для твердых объектов. Примером этого является гелий-4 — атом гелия с двумя протонами и двумя нейтронами.

В газе комнатной температуры тот факт, что два бозона могут быть в одном и том же состоянии, не имеет значения: при высоких температурах и низких концентрациях существует большой диапазон доступной энергии и положений, так что очень редко две частицы газа находятся в одном и том же состоянии. Однако по мере увеличения плотности газа его частицы располагаются все ближе друг к другу, но пока не соприкасаются. Если температура очень низкая, молекулы также имеют довольно небольшую энергию, и это означает, что число доступных энергий также очень невелико. Именно здесь вступает в игру статистика Бозе — Эйнштейна.

Согласно статистике Бозе — Эйнштейна, два бозона могут быть в одном и том же состоянии. То есть если сильно охлаждать газ и одновременно сжимать его, наступит момент, когда молекулы газа окажутся очень близко друг к другу и будут иметь очень маленький диапазон доступной энергии. Это приведет к тому, что некоторые молекулы войдут в одно и то же состояние, то есть будут иметь одно и то же положение и энергию. Если мы достаточно охладим газ, мы сможем добиться того, что это сделают все молекулы, то есть все вещество газа будет вести себя как одна-единственная молекула, и это состояние материи отличается от газообразного, твердого или жидкого. Оно называется конденсатом Бозе — Эйнштейна. За последние десятилетия конденсат перестал быть теоретическим курьезом и может быть создан в лабораторных условиях.

На следующем графике показана вероятность нахождения бозона с некоторой энергией для низких температур в сравнении с той же вероятностью по распределению Максвелла — Больцмана. При высоких температурах оба распределения совпадают.

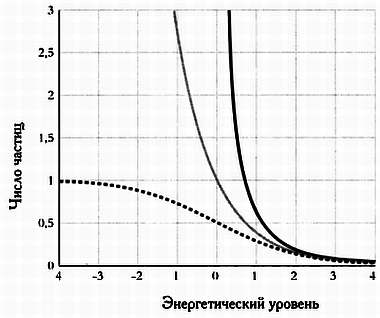
Число частиц на энергетический уровень для распределений Бозе — Эйнштейна (темно-серый) и Максвелла — Больцмана (светло-серый). Пунктиром показана статистика Ферми — Дирака.

Если же частицы, образующие газ, являются фермионами, их поведение при высокой плотности и низких температурах сильно отличается. Фермионы следуют другому типу статистики, называемой статистикой Ферми — Дирака. В этом случае два фермиона не могут быть в одном и том же состоянии. Пример фермиона — электрон, частица с отрицательным зарядом, которая вращается вокруг атомного ядра. Согласно статистике Ферми — Дирака, у двух электронов, вращающихся вокруг ядра, должны быть различные состояния, поэтому на каждый энергетический уровень может быть только два электрона: при одной и той же энергии у них будет разное внутреннее вращение. В результате не все электроны могут располагаться на орбите, ближайшей к атомному ядру, что, в свою очередь, порождает химические свойства вещества. То есть химия — это прямое следствие из статистики Ферми — Дирака.