Глава 2. Деньги и инфляция

Глава 2. Деньги и инфляция

Деньги — это прежде всего общепринятое средство платежа, используемое при купле-продаже товаров и услуг или финансовых операциях. Они используются как для обмена, так и для измерения стоимости товаров. Следовательно, деньги — это единица измерения ценности вещей, а также платежный инструмент. Физически деньги представляют собой металлические монеты или банковские билеты, но они могут быть и единицей измерения остатка на нашем банковском счете или карте — на ее чипе или магнитной полосе с использованием современных методов шифрования хранится информация о карте и ее держателе.

Краткая история денег: от товарных денег к фидуциарным

С течением времени деньги довольно сильно видоизменились. Изначально торговля основывалась на обмене товарами: люди обменивали излишки, накопленные одним сообществом, на излишки, накопленные другим. Вскоре некоторые товары, например скот, стали использоваться при обмене как базовые для оценки стоимости других товаров. Так, например, двадцать амфор оливок по стоимости равнялись одной овце, сто амфор вина — волу. Амфоры емкостью от 25 до 30 литров, наполненные водой, назывались талантами и выступали единицами веса, а позднее так стали называть денежные единицы.

Использование голов скота как платежной единицы привело к тому, что их изображения появились на камнях, глиняных табличках, а позднее — на металлических монетах. Впоследствии монеты стали чеканиться из драгоценных металлов, таким образом, стоимость монеты равнялась стоимости металла, из которого она была отчеканена (такие деньги называются товарными, или натуральными).

Следующим шагом стала чеканка монет из менее ценных металлов, и стоимость металла, из которого изготавливалась монета, была значительно меньше ее номинала. Такие деньги стали называться фидуциарными (от лат. fiducia — «доверие»)[1], или символическими, и этот этап их эволюции завершился с появлением бумажныхденег. Так как деньги чеканились из бронзы, серебра или золота, купцы позднего Средневековья обращались к ювелирам, чтобы те, взвесив наиболее ценные монеты, определили их реальную стоимость. Ювелиры и стали первыми банкирами: они принимали ценности на хранение, выдавая при этом свидетельства-расписки. Вскоре купцы стали считать эти свидетельства удобной и безопасной заменой самих монет.

Позднее на смену распискам пришли банковские билеты, и появились первые банки.

В древности ценность монет зависела от материала, из которого они были отчеканены. На фото — бронзовый римский сестерций.

В банках хранились вклады, за которыми владельцы обращались нечасто. Вскоре ювелиры и банкиры поняли, что достаточно хранить постоянно лишь небольшое количество ликвидных средств своих клиентов, а остальные вклады можно выдавать в виде займов при условии сохранения определенного коэффициента ликвидности, — так появились банковские деньги. Когда собственник клал деньги в банк, а банк выдавал их в виде займа третьему лицу, то эти деньги формально находились у трех разных людей: владельца вклада, банкира и заемщика, — отсюда следует определение денежной массы как суммы наличных денег на руках у населения и банковских вкладов.

Денежные стандарты, фидуциарные деньги и счетные денежные единицы

Денежный стандарт — это металл, для которого при предъявлении банку-эмитенту гарантирована конвертация в металлические монеты или банковские билеты. В основе каждой денежной системы лежит определенный металл: золото, серебро или их сплав.

Государство и банки — эмитенты бумажных денег гарантируют автоматический обмен драгоценного металла, лежащего в основе денежного стандарта, на банковские билеты. Фидуциарные деньги появились благодаря уверенности общества в банке-эмитенте, который гарантирует обратный автоматический обмен денег на драгоценный металл.

Семья Фуггеров стала одной из главных коммерческих и финансовых организаций XV–XVI веков. На иллюстрации Карл V слушает Якоба Фуггера, благодаря поддержке которого он взошел на трон.

Золотой стандарт использовался вплоть до Первой мировой войны. В 1944 году он был модифицирован в золотовалютный стандарт, основанный на двух твердых валютах, для которых гарантировался обмен на золото: американском долларе и британском фунте стерлингов. Так как все страны производили международные платежи в этих твердых валютах, они постепенно начали использовать эти же валюты для своих резервов, пока в 1971 году Соединенные Штаты Америки не объявили об отмене конвертируемости доллара в золото, что способствовало окончательному отказу от использования золотого стандарта. Ему на смену пришел фидуциарный стандарт, основанный на доверии к определенным твердым валютам, составляющим основу резервов центральных банков разных стран.

Отель «Маунт Вашингтон» на курорте Бреттон-Вудс, где в 1944 году прошла валютно-финансовая конференция Организации Объединенных Наций. На ней был подписан ряд соглашений взамен тех, что были заключены во время Первой мировой войны. Бреттон-Вудские соглашения утратили силу в 1971 году, когда Соединенные Штаты Америки объявили об отмене конвертируемости доллара в золото.

Валюты и виды обмена: почему одни деньги дороже других

Деньги, выпущенные центральными банками иностранных государств, называются валютой и являются средством платежа при международной торговле. Как правило, расчеты при этом ведутся в валюте страны-экспортера, однако часто предпочтение отдается твердым валютам, в частности американскому доллару или евро. Цена денежной единицы одной страны, выраженная в денежной единице другой страны, называется валютным курсом. Валюты являются конвертируемыми, если их можно обменивать на другие валюты по курсу, определяемому рынком, то есть по гибкому, свободному курсу.

Таким образом, на валютном рынке доллар ($) может котироваться по определенному курсу по отношению к евро (€): $1 = €0,69 (или, что аналогично, для покупки 1 евро требуется заплатить 1,449 доллара). В свою очередь, обменный курс фунта стерлингов (?) может равняться, например, €1,11 или $1,61, курс японской иены (?) — ?0,0067, €0,0075 или $0,0108. Это означает, что если мы покупаем в США автомобиль, который стоит 10000 долларов, а в нашем распоряжении есть только евро, сначала нужно купить доллары на сумму 6900 евро. Если же у нас на руках только фунты стерлингов, то потребуется заплатить 10000/1,61 = 6211,18 фунта стерлингов.

Если валютный курс фиксирован, это означает, что руководство страны установило для своей национальной валюты по отношению к валютам других государств определенный неизменный курс, который может колебаться лишь в строго заданных границах. Курс свободно конвертируемых валют колеблется в определенном интервале по отношению к другим валютам, причем желательно, чтобы колебания не превосходили 1 %, иначе это повлияет на стабильность валютного обмена.

Валютный курс государства оказывает огромное влияние на конкурентоспособность страны на мировом рынке. Если инфляция внутри страны высока, товары, произведенные на ее предприятиях, дорожают, что снижает возможности экспорта и, как следствие, уровень торговой активности со всеми возможными негативными последствиями для рынка труда. По этой причине страны с высоким уровнем инфляции вынуждены девальвировать свою валюту по отношению к остальным, чтобы повысить конкурентоспособность своих производителей на международном рынке.

Говорят, что первая валюта обесценивается по отношению ко второй, когда для ее приобретения требуется меньшее количество второй валюты. Так, если доллар обесценивается по отношению к евро, это означает, что для покупки 1 евро требуется, например, 1,60 доллара вместо прежних 1,449, то есть чтобы купить 1 евро, теперь требуется платить более высокую цену, так как доллар по отношению к евро обесценился.

Одна и та же валюта может обесцениваться по отношению к одним и одновременно расти в цене по отношению к другим валютам. Происходит это из-за того, что, в дополнение к валютным колебаниям, в этих странах меняются индексы цен.

Так, например, если в стране 1 зарегистрирован рост цен р₁ больший, чем рост цен р₂ в стране 2, обменный курс валют этих двух стран будет изменяться в зависимости от изменения индексов цен в этих двух странах. Если обменный курс валют этих стран равен E, он будет меняться в зависимости от относительного изменения роста цен р₁ и р₂, а именно:

Если цены в стране 1 увеличились больше, чем в стране 2, то обменный курс возрастет, то есть валюта страны 1 обесценится. И наоборот, если цены в стране 2 увеличатся больше, чем в стране 1, валюта страны 1 подорожает по отношению к валюте страны 2.

* * *

ПАРИТЕТ ПОКУПАТЕЛЬНОЙ СПОСОБНОСТИ И СТОИМОСТЬ ВАЛЮТ

Чтобы ответить на вопрос, почему одни валюты стоят больше, чем другие, введем еще одно понятие: паритет покупательной способности одной валюты по отношению к другой. На один доллар можно приобрести определенный набор продуктов, однако за эквивалент одного доллара в другой валюте по текущему обменному курсу можно приобрести больше или меньше продуктов.

Подумайте, можно ли купить за 69 евроцентов тот же набор продуктов, что и за один доллар?

Или за 69 евро — в сто раз больше продуктов, чем количество, купленное за один доллар, то есть столько же, сколько можно купить за 100 долларов? Очевидно, что если доллар обесценивается на 10,4 % по отношению к евро, то чтобы купить набор продуктов стоимостью в один доллар, потребуется всего 62,5 евроцента, а не 69 евроцентов, как раньше.

Например, если мы покупаем фотоаппарат, который в США стоит 150 долларов при обменном курсе $1- €0,69, то его стоимость составит €0,69/$ 1?$150 = 103,50 евро.

Если доллар обесценивается по отношению к евро на 10,4 % и обменный курс снижается до $1 = €0,625 (или €1 = $1,6), то в этом случае фотоаппарат станет для нас дешевле, если мы будем платить в евро: €0,625/$1?$150 = 93,75 евро.

Может случиться так, что евро обесценится по отношению к доллару (или, что аналогично, доллар повысится в цене по отношению к евро), и его курс станет равным $1,25 за €1 ($1 = €0,80).

В этом случае фотоаппарат обойдется нам дороже, чем европейским покупателям: €0,80/$1?$150 = 120 евро.

Поэтому когда страна обесценивает свою валюту по отношению к валюте другой страны, экспортируемые ею товары оказываются за границей дешевле, а товары, импортируемые этой страной, дорожают. В этом случае говорят, что покупательная способность валюты снижается.

* * *

С другой стороны, условия торговли определяются как отношение средних цен экспорта к средним ценам импорта, то есть:

Чем лучше условия торговли в стране, тем больше у нее преимуществ при международной торговле: хорошие условия торговли означают, что страна продает товары по высоким ценам, а взамен получает намного больше импортных товаров по более низким ценам. В международной торговле все страны стремятся получить сравнительное преимущество, то есть хотят экспортировать и импортировать определенные товары при благоприятных для себя условиях торговли.

Курсы различных валют являются следствием сделок, совершаемых на финансовых рынках и определяемых потребностями в международных платежах, которые испытывают различные учреждения: коммерческие и центральные банки, транснациональные корпорации, финансовые институты (инвестиционные фонды, пенсионные фонды, страховые компании и т. д.). Наибольшим спросом пользуются валюты, которые чаще всего применяются в международных расчетах. Как правило, это валюты стран с наиболее сильной экономикой.

Спрос на валюту также определяют базовые процентные ставки в странах с этой валютой, а также ожидания участников рынка относительно ее будущих котировок.

На курсы некоторых валют также влияют решения, принимаемые центральными банками государств для поддержания заниженного курса с целью стимулирования экспорта. Так, США, Китай и Япония поддерживают заниженные курсы своих валют по отношению к евро для стимулирования международной торговли.

Простые практические алгоритмы

Расскажем о простейших правилах арифметики в торговле, которые использовались начиная с эпохи Возрождения и до конца XX века. Первое из них — правило пропорции, позволяющее решать задачи, в которых две переменные прямо пропорциональны друг другу (с увеличением одной увеличивается и другая). Если, например, ростовщик зарабатывает три динара на займе в 50 динаров, сколько он заработает на займе в 120 динаров?

50 динаров ____ 3 динара

120 динаров ___ х динаров.

Как известно, эта задача решается так:

50/120 = 3/х

50х = 120-3

50х/50 = 120?3/50

х = 120?3/50 = 7,20 динара.

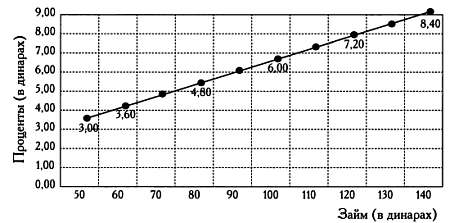
Правило пропорции.

Похожи на них задачи с обратной пропорциональностью. Два каменщика строят стену за 12 дней. Сколько дней понадобится на постройку стены пяти каменщикам?

2 человека ___ 12 дней

5 человек ____ х дней.

Задача решается следующим образом:

2/5 = х/12

2?12 = 5х

5х/5 = 2?12/5

х = 2?12/5 = 4,80 дня = 4 дня 19 часов 12 минут.

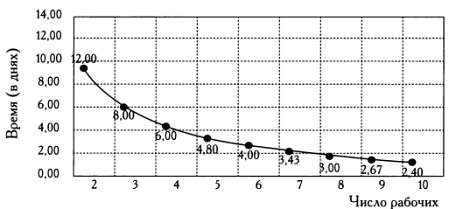
Второй вариант использования правила пропорции.

Наконец, правило пропорции применимо и для решения более сложных задач: если 40 маляров, работая по 8 часов в день, красят 320 метров забора за 10 дней, то за сколько дней 55 маляров покрасят 440 метров такого же забора, если будут работать по 6 часов в день?

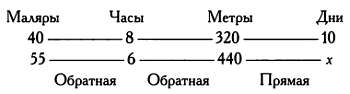
Задача решается следующим образом:

10/х = 55/40?6/8?320/440

х = 10?440/320?8/6?40/55 = 13,3 дня = 13 дней 8 часов.

Определенная сумма

Греческая буква ? (заглавная сигма) очень часто используется в математических формулах экономической теории и обозначает сумму слагаемых. Например, для обозначения суммы x₁  + х₂ + х₃  + х₄  можно использовать выражение ? ⁴_i=1 x_i

Знак ? перед х_i означает, что нужно сложить все значения х. Числа, указанные под буквой ? и над ней, обозначают границы суммы, то есть наибольшее и наименьшее значение индекса, которое используется при сложении.

Сумма ? ⁶_k=3 x_k означает х₃ + х₄ + х₅ + х₆,

Cумма ? ⁿ_j=m x_j означает х_m + х_m+1 … + х_n-1 + х_n.

Индексы могут принимать только целые значения, а нижний индекс может быть обозначен любой буквой.

Так, ? ^m_i=1 x_i = ? ^m_j=1 x_j = ? ^m_k=1 x_k

Член, следующий за буквой ?, называется слагаемым. В выражении ? ^m_k=1 x_k слагаемыми являются х_k.

* * *

УРАВНЕНИЯ И НЕРАВЕНСТВА

Уравнение — это математическое равенство с одной или несколькими неизвестными величинами.

Уравнение обращается в верное равенство лишь при определенных значениях этих неизвестных. Неизвестная в уравнениях может быть возведена в квадрат или в куб.

Например, х + 12 = 25 — Зх — уравнение первой степени, 12 + х² — 6х = 3 — уравнение второй степени, 9 — Зх² — 6х³ = -12 — уравнение третьей степени.

В XIII веке Леонардо Пизанский решал задачи, подобные следующей: у ювелира есть золото 975-й пробы и золото 750-й пробы, и он хочет получить слиток золота 900-й пробы весом в два килограмма.

Сколько золота каждой пробы потребуется для этого? Эта задача решается так:

х кг вес золота 975-й пробы

(2 — х) кг вес золота 750-й пробы

х?0,975 + (2 — х)?0,750 = 2?0,900

х?0,975 + 2 0,750 — 0,750?х = 1,800

х?0,975 — 0,750х = 1,800 — 2?0,750

х?0,225 = 1,800 — 1,500

х?0,225 = 0,300

х = 0,300/0,225 = 4/3 = 1 1/3 кг золота 975-й пробы

(2 — х) = 2 – 1 1/3 = 2/3 кг золота 750-й пробы.

Фибоначчи также сформулировал и решил задачи, описываемые уравнениями второй степени, подобные следующей: площадь прямоугольного поля равна 2400 м² Известно, что его длина на 20 м больше ширины. Вычислите размеры поля. Таким образом, произведение ширины (х) на длину (х + 20) равно 2400 м². Стандартное уравнение второй степени выглядит так: ах² + Ьх + с = 0. Значение неизвестной х можно вычислить по формуле:

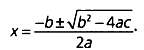
В этом случае:

х?(х + 20) = 2400; х² + 20х = 2400; х2 + 20х — 2400 = 0.

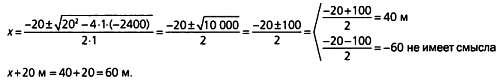
Таким образом, поле имеет размеры 40 х 60 м.

Неравенства похожи на уравнения, однако вместо знака равенства (-) содержат один из четырех возможных знаков неравенства:

<= «меньше либо равно»

< «меньше» (строго)

>= «больше либо равно»

> «больше» (строго).

Неравенству с одной переменной х — 7 > 13 удовлетворяют все числа, которые при уменьшении на 7 равняются 13 или более. Неравенства решаются по схожему алгоритму. Пример:

х — 7 >= 13; х — 7 + 7 >= 13 + 7; х >= 20.

Решением этого неравенства является множество всех чисел, больших или равных 20.

Иногда уравнения и неравенства ведут себя по-разному, как, например, в следующем случае.

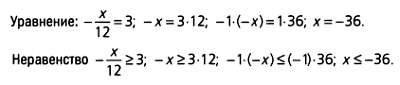
Здесь для решения неравенства нужно сменить его знак на противоположный.

Это можно показать так: 7 < 13, однако, напротив, — 7 > — 13.

* * *

Сумма первых восьми нечетных чисел записывается следующим образом:

? ⁿ_j=0 (1 + 2j) = (1 + 2?0) + (1 + 2?1) + (1 + 2?2) + (1 + 2?3) + (1 + 2?4) + (1 + 2?5) + (1 + 2?6) + (1 + 2?7) + (1+ 2?8) = 1 + 3 + 5 + 7 + 9 + 11+ 13 +15 + 17.

Сумма ? ⁵_j=2 2^j равняется 2² + 2³ + 2⁴ + 2⁵ = 4 + 8 +16 + 32.

Сумма ? ³_l=1 (l+1)?3^l = 2?З¹ + 3?З² + 4?3³ = 6 + 27 + 108.

* * *

ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ ПЕРЕМЕННЫЕ

Во многих областях современной математики переменная определяется как дискретное множество (это означает, что она может принимать только определенные значения, и между двумя соседними значениями не может находиться никакого другого). На языке математики это записывается так: {х₁, х₂, …,х_n}. Между значениями х₁ и х₂ нет никакого другого значения переменной х.

Существуют и другие переменные, используемые намного чаще, которые определены на непрерывных множествах (это означает, что такие переменные могут принимать целые, дробные и иррациональные значения). Примером такой переменной является {0 <= t <= }. Очень часто для решения различных задач, связанных с функциями, определенными на непрерывных множествах, требуется выполнить операцию интегрирования 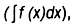 , как, например, в случае с функцией вероятности или нормальным распределением вероятности. Когда речь идет о дискретных переменных, операцией, аналогичной интегрированию, является сложение.

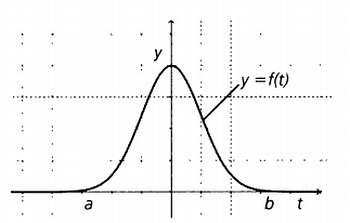
Функция f(t) непрерывной переменной t, определенная на множестве {a <= t <= b}.

Функция у(х) дискретной переменной х, определенная на множестве {х₁, х₂, х₃, x₄}.

Множество из четырех элементов можно обозначить буквами и цифрами, которые будут выступать в качестве индексов: х₁, х₂, х₃, x₄.Если мы хотим работать с множеством из n элементов (n может изменяться в зависимости от задачи), они будут обозначаться {х₁, х₂…. х_n-1, x_n}. Так, х_{n - 1} обозначает элемент, идущий перед х_n, последним элементом множества. Произвольный элемент ряда (занимающий в нем i-е место) обозначается х_i. Таким образом, например, цены четырех товаров можно обозначить p₁, р₂, р₃ и р₄, а запрошенные объемы каждого товара — q₁, q₂, q₃ и q₄.

* * *

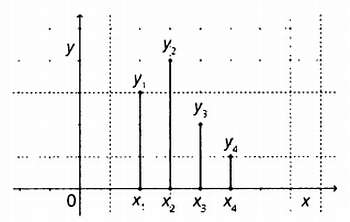
Определенная сумма применяется при записи математических рядов, например биномиального ряда. Биномиальное распределение вероятности используется при анализе результатов опросов, когда на вопрос возможны лишь два ответа (например, «да» и «нет»). Вероятность их появления равняется р и q. А поскольку сумма их вероятностей равна р + q = 1, следовательно, q = 1 — р.

Чтобы узнать вероятность того, что будет получено три или менее ответа «да», нужно вычислить вероятности следующих событий: ни одного ответа «да», один ответ «да», два ответа «да» или три ответа «да», то есть Р (0 < k < 3) = Р (0) + Р (1) + Р (2) + Р (3). Эту же формулу можно записать так:

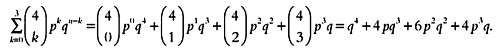
Функция, позволяющая вычислить вероятность того, что на п вопросов будет дано от 0 до k ответов «да», равна сумме вероятностей, последним слагаемым в которой будет Р(k). Эта же формула записывается в следующем виде:

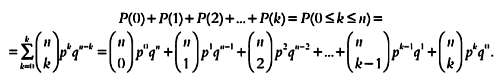
В похожем виде записываются статистические функции, к примеру:

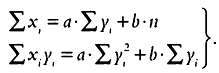
Эта же формула в виде ряда будет записываться так:

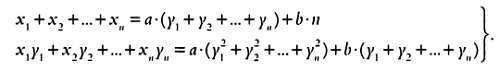
Аналогичный вид имеют статистические формулы:

Как измеряется инфляция. Виды индексов

Инфляция — это повышение цен на товары и услуги, при которой зарплаты или доходы потребителей не меняются и, таким образом, их покупательная способность снижается. Это означает, что на ту же сумму денег, что и раньше, можно купить меньше товаров. Чтобы измерить инфляцию, необходимо проанализировать изменения цен. Высокая инфляция негативно сказывается на экономике страны, так как уровень доходов потребителей и домохозяйств снижается, одновременно с этим ухудшается конкурентоспособность страны на мировом рынке. Следовательно, инфляцию необходимо контролировать. Стабильность цен — одна из необходимых характеристик здоровой экономики государства.

Колебания цен измеряются с помощью индексов. При расчете инфляции рассматриваются средние цены потребительской корзины товаров и услуг, в которой различным ценам присваиваются весовые коэффициенты. Выбранный год рассматривается в качестве исходного, и ему присваивается значение 100, на основе которого рассчитывается рост средневзвешенных цен в последующие годы.

Так, например, если в качестве базового выбран нулевой год с индексом 100, и в последующие годы зарегистрированы приведенные ниже показатели роста цен, индекс цен изменится так:

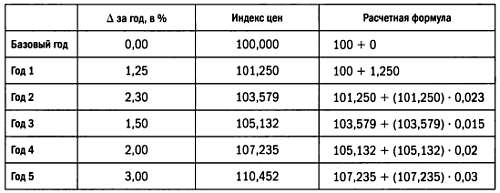
Расчет индекса цен.

Статистические организации государства разрабатывают различные индексы цен для разных продуктов. Самым известным является индекс потребительских цен, рассчитываемый на основе фиксированной корзины определенных продуктов и обязательных расходов потребителей (продукты питания, одежда, коммунальные услуги, образование, общественный транспорт ит.д.). Так же формируются индексы цен для других продуктов, например промышленных, сельскохозяйственных, строительных товаров, индекс цен на недвижимость и т. д.

Годовой уровень инфляции (в %) рассчитывается по следующей формуле:

Существует множество теорий, объясняющих рост цен. Некоторые из них записаны на языке алгебры, как, например, количественная теория денег Ирвинга Фишера. Согласно этой теории уровень цен (Р) в стране зависит от общего объема всех товаров и услуг (Q), количества денег в обращении (М) и скорости обращения денежной массы (V), показывающей, сколько раз деньги переходят из рук в руки:

Р?Q = М?V.

* * *

ИНДЕКСЫ ЦЕН

Для количественной оценки изменения цен, объемов производства или стоимости за определенный период времени используется огромное количество различных индексов. Если мы хотим рассчитать глобальные индикаторы изменения цен или объемов производства в стране, нужно рассмотреть соответствующие временные ряды. Цены сравниваются с ценами определенного года, выбранного в качестве базового. Индексы производства рассчитываются при неизменном уровне цен, индексы цен — при неизменных объемах производства.

Наиболее популярные индексы производства и цен — это индексы Ласпейреса (Q_L, P_L), Пааше (Q_p, P_р) и Фишера (Q_F, P_F).

где Р — цена, Q — объем производства, ?p₀q_t, обозначает общую стоимость всей продукции, выпущенной за год t при неизменных ценах р₀ года 0, а ?p₀q₀ стоимость всей продукции, произведенной в стране за год 0. Аналогично рассчитываются индексы при неизменных ценах.

Индекс Фишера является средним геометрическим индексов Ласпейреса и Пааше.

* * *

Американский экономист Ирвинг Фишер (1867–1947) совершил множество открытий в области экономической теории, в частности описал уравнения количественной теории денег.

Если выразить из этого равенства переменную Р, получим новое уравнение: Р = М?V/Q. Из него нетрудно понять, что цены возрастают с ростом М (денежной массы на руках у населения) при условии, что остальные две переменные, V и Q, остаются неизменными, либо если возрастает V — скорость обращения денег. Цены снижаются, когда уменьшается денежная масса или скорость обращения денег. Изменение цен обратно пропорционально изменению количества товаров и услуг: если предложение растет, а объем денежной массы и скорость обращения денег остаются неизменными, цены снижаются, если объем производства падает, цены растут.

Существуют другие теории и математические модели, объясняющие инфляцию, например кривая Филлипса. Олбан Филлипс связывал уровень инфляции с уровнем безработицы: он проанализировал статистические данные Великобритании и представил их на графике, на оси ординат которого откладывался уровень инфляции, на оси абсцисс — уровень безработицы. Кривая Филлипса является нисходящей и по своему поведению напоминает кривую спроса: при росте цен уровень спроса снижается. В итоге Филлипс получил обратную зависимость между уровнем безработицы и инфляцией, основной причиной которой являлся рост зарплат. Иными словами, с ростом инфляции уровень безработицы снижается и, напротив, политика сдерживания цен приводит к росту безработицы.

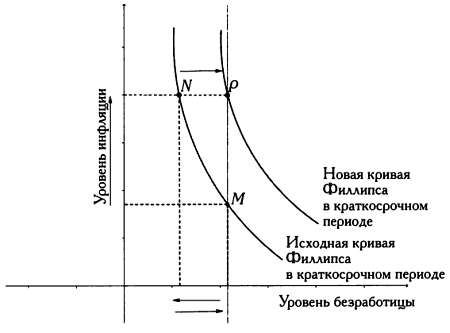
Кривая Филлипса.

Рост цен может быть вызван разными причинами: например, избыточным повышением спроса при неизменном уровне производства (предложения) — этот процесс известен как инфляция спроса. Причиной инфляции также могут стать рост зарплат как следствие снижения безработицы и увеличение цен на сырье. Цены растут, однако уровень безработицы остается неизменным, а в условиях экономического роста цены повышаются еще быстрее. В XX веке наблюдался неизменный рост цен, в том числе и во время рецессии. В периоды рецессии может возникать инфляция издержек, иными словами, цены увеличиваются несмотря на одновременный рост безработицы.

В условиях сильной экономической рецессии могут складываться ситуации, когда цены снижаются. В этом случае идет речь о дефляции — отрицательной инфляции.

Дефляция возникает, когда из-за снижения объема выданных кредитов сокращается денежная масса, безработица растет и в то же время наблюдается перепроизводство, в итоге компании вынуждены снижать цены, чтобы распродать излишки.

Еще одним предельным случаем является гиперинфляция, возникающая, когда власти страны выпускают в обращение большие массы денег (иными словами, включают печатный станок на полную мощность), чтобы покрыть расходы или стимулировать потребительский спрос, при этом структура производства в стране не меняется, а уровень производства находится на прежнем уровне или даже снижается. Гиперинфляция обычно выражается трехзначными числами и более и порой превышает 1000 %. Высокая инфляция, достигающая нескольких сотен процентов в год, называется галопирующей.

В периоды экономической рецессии, как, например, во время экономического спада в начале 1970-х, вызванного нефтяным кризисом, отмечается значительный рост цен вкупе с ростом безработицы. Такая ситуация называется стагфляцией.

В 1920-е годы, когда Германия страдала от гиперинфляции, не знавшей аналогов в истории, на смену банкнотам в тысячу марок пришли банкноты в миллиард марок.

Процентная ставка: стоимость денег

Номинальная стоимость денег, по сути, всегда неизменна: один доллар — это один доллар, один евро — это один евро, один фунт стерлингов — это один фунт стерлингов. Эта неизменность позволяет использовать деньги как единицу расчета стоимости товаров, услуг, недвижимости, земли, а также общепринятое средство платежа, имеющее конкретную физическую форму — металлических монет, банковских билетов и т. д. Однако стоимость товаров и услуг меняется и с течением времени за одну и ту же сумму денег — в случае если цены растут — можно купить все меньше товаров. Это означает, что покупательная способность денег снижается, или, другими словами, для приобретения прежнего количества товаров нужно больше денег.

Стоимость денег меняется в зависимости от того, сколько товаров можно на них купить. Во время инфляции стоимость денег снижается, при снижении цен (дефляции) происходит обратный процесс. Однако деньги обладают еще одним неотъемлемым качеством — ликвидностью, то есть возможностью использования в качестве средства платежа. Когда кому-либо не нужны ликвидные деньги, он может дать их взаймы третьему лицу, которому они необходимы для приобретения каких-либо товаров. Взамен третье лицо возвращает долг в размере, превышающем полученную сумму. Эта дополнительная сумма, которую готов платить должник за предоставленный займ, называется процентной ставкой. Таким образом, процентная ставка — это цена денег.

Процентная ставка определяется как количество процентов от заемного капитала, которые должны быть уплачены за пользование им. Так, если мы получили займ в 1000 евро на три года с процентной ставкой 5 % годовых, каждый год мы будем должны заплатить 50 евро процентов. К концу срока займа, когда мы вернем его полностью, мы заплатим всего 1150 евро.

Представим ситуацию: потребителю нужна определенная сумма денег для покупки товара, предпринимателю — для покупки оборудования, при этом ни у того, ни у другого недостаточно денег для удовлетворения своих потребностей. Они обращаются в банк и, получив нужную сумму, обязуются вернуть ее в указанный срок и заплатить определенную цену за возможность использовать эти деньги. Цена, которую они заплатят за деньги, полученные взаймы, называется процентной ставкой. С другой стороны, некий человек, у которого есть лишние деньги, согласен снизить их ликвидность и поместить их на банковский вклад за определенный процент от этой суммы. Следовательно, деньги имеют свою цену не только для заемщиков, которым нужно вернуть займы с процентами, но и для банка, которому, чтобы привлечь деньги клиентов, необходимо заплатить им.

Процентная ставка также является ценой, уплачиваемой за определенные финансовые активы. Так, если власти страны, стремясь привлечь средства населения, выпускают государственные облигации, казначейские векселя и другие ценные бумаги, то, помимо срока погашения, на них указывается и определенная процентная ставка. Например, государство может выпустить облигации под 3,5 % либо краткосрочные векселя на срок 3 или 6 месяцев под 1 % и 1,5 % соответственно. Частные компании также могут выпускать ценные бумаги с фиксированным доходом (например, облигации) с определенной процентной ставкой. Таким образом компании получают необходимые средства на рынке капитала, однако взамен им нужно будет уплатить определенную процентную ставку.

Процентные ставки центральных банков: EURIBOR, ставка ФРС и другие

Центральные банки разных стран устанавливают базовую (официальную) процентную ставку для контроля инфляции и денежной массы в обращении. Если процентная ставка снижается, количество денежной массы в обращении увеличивается, так как кредиты становятся дешевле. Чем больше денег находится в обращении, тем больше ликвидных платежных средств на руках у потребителей, в итоге растет спрос и, как следствие, цены. И наоборот, если экономический рост слишком высок и инфляция растет, центральные банки (Федеральная резервная система, Европейский центральный банк и другие) стремятся поднять процентные ставки, чтобы замедлить потребление и рост цен.

Базовые процентные ставки в разных странах и денежных зонах отличаются.

Так, в январе 2010 года процентная ставка, установленная Федеральной резервной системой США, находилась на уровне 0,25 %, ставка Европейского центрального банка — 1 %, ставка Банка Англии составляла 0,50 %, ставка Банка Японии — 0,10 %, Банка Канады — 0, 25 %, Резервного банка Австралии — 3,75 %, Национального банка Швейцарии — 0,25 % и т. д. Официальная базовая процентная ставка используется в качестве отправной точки при определении ставок межбанковских кредитов, то есть процентной ставки, под которую банки дают займы друг другу.

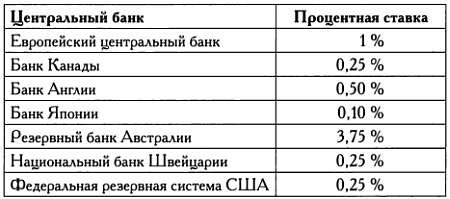
Официальные базовые процентные ставки (на январь 2010 года).

Эти межбанковские процентные ставки, как правило, немного выше, чем базовые процентные ставки. Так, EURIBOR — это межбанковская процентная ставка в еврозоне. Она рассчитывается на основе межбанковских ставок, используемых при сделках на открытом рынке ведущими европейскими банками, и является основой при расчете процентов по большинству кредитов. Выдавая любой потребительский или ипотечный кредит, банки обычно используют EURIBOR (или межбанковскую ставку Банка Англии или ФРС, если речь идет об Англии или США соответственно) в качестве базисной процентной ставки и увеличивают ее на несколько пунктов.

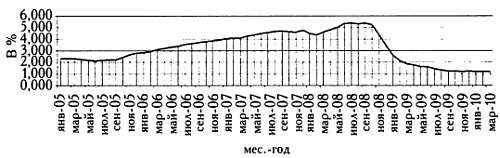
Колебания ставки EURIBOR в 2005–2010 годах.

По сути, для каждой кредитной операции существует отдельная ставка EURIBOR в зависимости от срока выдачи кредита: 1 месяц, 3 месяца, 6 месяцев, 12 месяцев и т. д. Межбанковские процентные ставки ФРС, Банка Англии и Банка Японии для займов сроком в 1 день, 3 месяца или 1 год также отличаются. Расчет EURIBOR выполняется ежедневно до И утра на основе ставок, используемых 64 основными европейскими банками, по следующей схеме: крайние значения (15 % самых высоких и 15 % самых низких ставок) отбрасываются, после чего рассчитывается среднее арифметическое. Дневная межбанковская ставка EONIA рассчитывается Европейским центральным банком на основе дневных межбанковских ставок, используемых 48 европейскими банками.