Глава 3 История групп
Глава 3 История групп
Математика — всего лишь история групп.
Анри Пуанкаре
ВЕЙЛЬ: Присаживайтесь, господин Леви-Стросс.
ЛЕВИ-СТРОСС: Вы объясните мне, что такое группа?
ВЕЙЛЬ: Постараюсь. Мне хотелось бы начать с одного примера — он очень прост, но в нем постепенно раскрывается большинство основных понятий теории групп. Представьте себе равносторонний треугольник — надеюсь, вы помните, что это треугольник, все стороны которого равны. Меня интересуют движения, которые не меняют положение треугольника, то есть такие, когда сторонний наблюдатель не сможет увидеть разницу между треугольниками «до» и «после». Говорят, что треугольник инвариантен относительно таких преобразований.
ЛЕВИ-СТРОСС: Простите, я перебью вас, господин Вейль. Я кое-что не понял: если фигура в результате этих преобразований не меняется, то как определить, выполнили мы это преобразование или нет? Ведь треугольники не имеют памяти!
ВЕЙЛЬ: Хороший вопрос. Я как раз собирался ответить на него. Нужно пронумеровать вершины треугольника. Он будет выглядеть так же, однако в результате преобразования положение вершин изменится, таким образом, преобразование оставит свой след. Вершины нумеруются исключительно из соображений удобства.
Первая разновидность движения, которую мы рассмотрим, — поворот на 120° против часовой стрелки относительно центра треугольника.
Обозначим это преобразование через R. Как я уже говорил, увидеть результат R нельзя, но если мы бы, к примеру, пронумеровали вершины треугольника, начиная с верхней, против часовой стрелки, то можно было бы сказать, что R переводит первую вершину в третью, вторую — в первую, третью — во вторую. Проще всего показать это на рисунке.
43
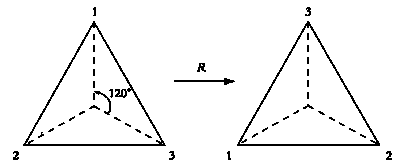
Результат поворота R.
Видите? Треугольник не изменился, но теперь его вершины пронумерованы 3—1—2, а не 1—2—3.
R не единственное преобразование, оставляющее треугольник неизменным.
Представьте себе осевую симметрию, ось которой пересекает треугольник. Чтобы в результате симметрии треугольник остался неизменным, нужно внимательно выбрать ось, так как при некоторых видах симметрии положение треугольника изменится.
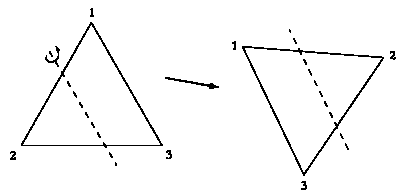
Симметрия, при которой треугольник меняется.
Треугольник останется неизменным, если ось симметрии проходит через его центр и одну из вершин. Поворот мы обозначили через R, симметрию — через S. Та же схема, которой мы проиллюстрировали поворот R, поможет показать, как изменится положение вершин при симметрии S. Первая вершина останется на месте, а вторая и третья поменяются местами. Теперь вершины пронумерованы не 1—2—3, а 1-3-2.
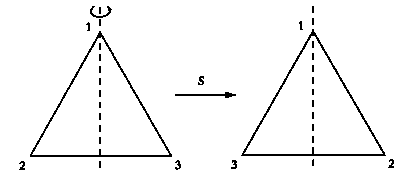
Результат симметрии S.
Теперь нам известны преобразования R и S. Что с ними можно сделать?
ЛЕВИ-СТРОСС: Выполнить сначала первое, а затем — второе?
ВЕЙЛЬ: Именно! Основное свойство этих преобразований заключается в том, что для двух таких преобразований можно определить их композицию. Применим поворот R, затем — симметрию S и обозначим полученный результат как SR. Мы привыкли читать слева направо, поэтому было бы логичнее записать RS, так как поворот R выполняется первым. Однако обозначение SR имеет свои преимущества.
Найдем композицию двух исходных преобразований.
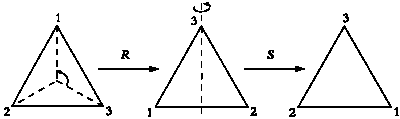
Композиция преобразований R и S.
На рисунке показано, что при движении SR вторая вершина остается неизменной, а две другие меняются местами. Следовательно, порядок следования вершин меняется с 1—2—3 на 3—2—1. Обратите внимание, что этот же результат можно
45
получить, применив к исходному треугольнику осевую симметрию, ось которой проходит через вторую вершину. Два этих преобразования совпадают.
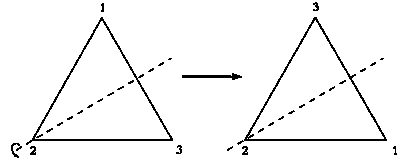
Композиция преобразований SR представляет собой симметрию.
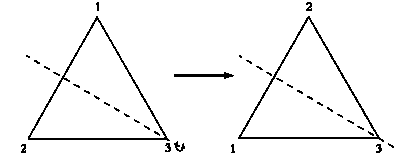
Теперь определим RS, то есть сначала применим S, а затем R, и посмотрим, как изменится порядок вершин.
ЛЕВИ-СТРОСС: Но от перемены мест множителей произведение не меняется.
ВЕЙЛЬ: Ах, эта юность, эта святая простота! Как же сложно по-новому посмотреть на то, что всем известно с детства. «От перемены мест множителей произведение не меняется» только при умножении чисел: трижды семь — то же, что и семью три. Однако нет никакой причины, по которой этот закон должен выполняться для других операций, например для сочетания движений, оставляющих исходную фигуру неизменной. Между прочим, это четко видно в нашем примере. Если сначала мы выполним S, а затем R, то получим...
Композиция преобразований S и R.
Вершины будут располагаться в порядке 2—1—3. Таким образом, результаты движений SR и RS отличаются.
46
ЛЕВИ-СТРОСС: Но RS — тоже симметрия.
Преобразование RS — симметрия.
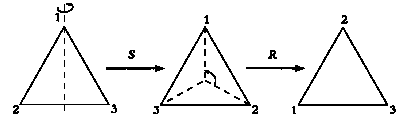
ВЕЙЛЬ: Да, и ее ось проходит через третью вершину. Для того чтобы при симметрии треугольник оставался неизменным, ось симметрии должна проходить через его центр и одну из вершин. На основе R и S можно определить все возможные разновидности такой симметрии. Если ось симметрии проходит через вторую вершину, это симметрия SR, если через третью — RS. Добавив к ним собственно симметрию S, ось которой проходит через первую вершину, получим полный перечень:
S, SR и RS — все возможные виды симметрии, оставляющие треугольник неизменным.
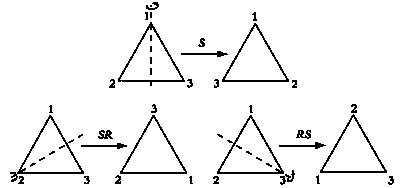
Виды симметрии, оставляющие треугольник неизменным.
ЛЕВИ-СТРОСС: Послушайте, господин Вейль, чтобы мы могли составить композицию двух преобразований, они обязательно должны отличаться?
47
ВЕЙЛЬ: Вовсе нет. Ничто не мешает применить одно и то же преобразование несколько раз подряд. Так как поворот фигуры два раза подряд на 120° равносилен повороту на 240°, движение RR также будет поворотом, при котором треугольник остается неизменным. Вместо RR будем записывать R2. Если мы повернем фигуру еще на 120°, она совпадет с исходной. Таким образом, R3 никак не изменяет треугольник. Мы не учли преобразование, которое оставляет порядок следования вершин неизменным — 1—2—3. Будем называть это преобразование тождественным и обозначим его через I. Обратите внимание, что композицией тождественного преобразования и любого другого движения будет это движение.
Мы доказали, что R3 = I, так как результатом трех поворотов является исходная фигура. Говорят, что порядок R равен трем. В общем случае порядок преобразования указывает, сколько раз его нужно применить, чтобы получить тождественное преобразование. S имеет порядок, равный двум — если мы повторим симметрию дважды, то получим исходный треугольник. Мы уже показали, что S, RS и SR — симметрии треугольника. Какие повороты оставляют фигуру неизменной? Обратите внимание, что поворот обладает этим свойством только тогда, когда угол поворота кратен 120°. Следовательно, все возможные повороты — это R, R2 и R3 = I.
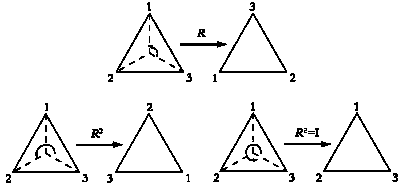
Повороты, оставляющие треугольник неизменным.
Мы описали все возможные виды симметрии (S, RS и SR) и все повороты (I, R, R2). Преобразования, оставляющие треугольник неизменным, определяются тем, как они меняют порядок его вершин. Так как поменять вершины треугольника местами можно всего шестью способами, мы описали все преобразования, обладающие этим свойством. Мы знаем, каковы результаты R и S, но не знаем, что получится, если мы применим сначала поворот R, а затем симметрию RS.
48
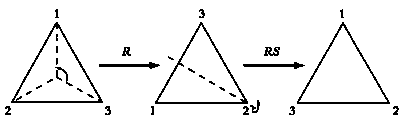
Преобразование (RS) R.
Как видите, при композиции этих преобразований порядок следования вершин меняется с 1—2—3 на 1—3—2. Таким же будет порядок вершин и при симметрии S, значит, (RS)R = S.
ЛЕВИ-СТРОСС: А что означают скобки?
ВЕЙЛЬ: Скобки указывают, в каком порядке выполняется композиция преобразований. Обратите внимание, что запись RSR априори неоднозначна: следует ли выполнить сначала преобразование R, а затем RS, как мы только что сделали, или же применить сначала SR, а затем R? В первом случае запишем (RS)R, во втором — R(SR). Результаты этих преобразований могут отличаться. Рассмотрим в качестве примера вычитание натуральных чисел. Результаты
7 - (5 - 3) = 7 - 2 = 5
и
(7 - 5) - 3 = 2 - 3 = -1
отличаются, и здесь крайне важно, как располагаются скобки. Впрочем, нам повезло: преобразования (RS)R и R(SR) совпадают.
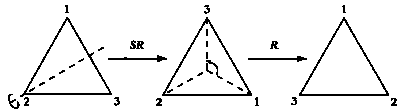
Преобразования R(SR) и (RS)R совпадают.
ЛЕВИ-СТРОСС: Столько информации! У меня голова идет кругом!
ВЕЙЛЬ: Неудивительно. Предлагаю вам представить результаты в «таблице умножения», подобной той, что мы учили в школе. В каждой клетке запишем композицию преобразований, указанных в соответствующей строке и столбце. Первой всегда будет преобразование, указанное в столбце, как показано стрелкой.
49
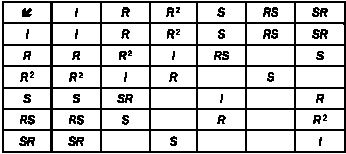
Пока что я записал в таблице только те преобразования, результат которых мы уже знаем: композицией любого преобразования и тождества будет исходное преобразование, RSR = S, a R3 = S2 = I. Эти результаты позволяют нам найти результат, например SRSR. Так как мы можем расставить скобки произвольным образом, получим: SRSR = S(RSR). Согласно приведенным выше равенствам, RSR = S, следовательно, SRSR= SS = S2 — это тождественное преобразование, так как порядок симметрии S равен двум. Следовательно, SRSR = I. Но таблица еще не закончена. Не хватает еще нескольких композиций, в частности SRS. Чтобы определить ее результат, напомню, что RSR = S. Если приписать в обе части равенства R2, получим R2RSR = R2S. Мы знаем, что R2R = R3 = I, следовательно, SR = R2S.
Мы получили еще одну композицию, результат которой известен. Мы по-прежнему можем приписать S в обе части равенства, на этот раз — справа. Получим SRS = R2S2, но так как S2 = I, имеем SRS = R2. Добавим результаты в таблицу.
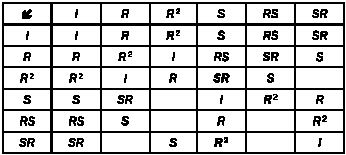
Но таблица все еще не закончена: не хватает композиций R2SR, SR2, RSR2, RSRS и SR2S. Их результаты можно получить на основе тех, что приведены выше — попробуйте сами! К примеру, R2SR совпадает с R(RSR). Но мы знаем, что RSR = S, следовательно, R2SR = RS. Аналогично:
SR2=(SR)R=(R2S)R=R(RSR)=RS,
50
ведь мы уже доказали, что SR = R2S. Я уже провел самые сложные вычисления, и все остальные расчеты вы можете выполнить самостоятельно. Попробуйте и поймете, удалось ли вам понять описанный метод. Как бы то ни было, важно, что эта таблица содержит всю информацию о множестве преобразований, оставляющих треугольник неизменным: что это за преобразования, каковы их композиции, какой порядок они имеют (то есть сколько раз их нужно выполнить последовательно, чтобы получить тождественное преобразование).
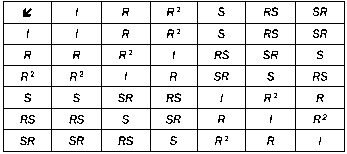
Таблица преобразований треугольника.
ЛЕВИ-СТРОСС: Господин Вейль, возможно, это прозвучит глупо, но пока вы заполняли таблицу, я вспомнил «Меланхолию I» Дюрера, одну из трех его «Мастерских гравюр», где изображена крылатая фигура, погруженная в раздумья о геометрии. Как вам известно, на гравюре можно видеть магический квадрат. Сумма чисел во всех его строках, столбцах, а также на диагоналях и некоторых других линиях одинакова и равна 34. Имеет ли этот магический квадрат что-то общее с вашими таблицами умножения?

51
ВЕЙЛЬ: Боюсь, что почти ничего. Важнейшее отличие между ними заключается в том, что в нашей «таблице умножения» все строки и столбцы содержат одни и те же элементы, а в магическом квадрате числа никогда не повторяются. В первой строке квадрата Дюрера записаны числа 16, 3, 2 и 13, во второй — 9, 10, 11 и 8: квадрат красив как раз тем, что все числа в нем различны. Наша таблица скорее напоминает латинский квадрат: символы содержатся в каждой строке и в каждом столбце ровно один раз. Пример:

Далее я объясню, что таблица умножения для группы с конечным числом элементов всегда будет латинским квадратом.
ЛЕВИ-СТРОСС: Прекрасно. Давайте вернемся к группам.
ВЕЙЛЬ: Я привел столь подробный пример с преобразованиями треугольника для того, чтобы теперь мы смогли вместе определить их внутреннюю структуру, то есть то общее, что остается, когда мы отбросим все частные случаи. Не будем откладывать дело в долгий ящик и начнем с того, что избавимся от треугольника.
Напомню, что предмет нашего изучения — не фигура сама по себе, а ряд ее преобразований, которые мы обозначили через R, S и так далее. Заменим их произвольным множеством элементов (конечным или бесконечным), которое будем обозначать буквой G. В примере с преобразованиями треугольника мы можем объединить два движения так, что получится третье, которое будет обладать теми же свойствами. Сохраним это условие: для каждой пары элементов G должна быть определена операция, результат которой также будет принадлежать G. Ранее мы обозначали эту операцию, просто записывая два члена рядом. Теперь введем для обозначения этой операции какой-нибудь новый символ, например *. Так, а * b будет обозначать результат умножения а на b согласно свойствам групповой операции.
На этом мы могли бы остановиться, но подобная структура не содержит достаточно ограничений, чтобы гарантировать наличие некоторых интересных свойств.
Если мы рассмотрим множество всего из трех букв, к примеру С = {х, y, z}, то найдется 19 683 разных способа определить на этом множестве операцию, которая сопоставит любым двум элементам третий. Это слишком много! Необходимо, чтобы операция * обладала некоторыми свойствами. Вернемся к примеру с преобразованиями треугольника. Напомню, что композиция любого преобразования с тождественным преобразованием I оставляла исходное преобразование неизменным.
52
Аналогично, нам нужен нейтральный элемент е такой, что равенства а*е = е*а = а будут верными для любого элемента а множества G. С учетом нейтрального элемента в примере с множеством {х, у, z} число возможных операций сократится до 81 — почувствуйте разницу! Крайне важную роль в расчетах сыграла возможность располагать скобки в произвольном порядке, поэтому мы введем новое требование: при операции над любыми тремя элементами результаты (а * b) * с и а * (b * с) должны быть равны. Это свойство называется ассоциативностью.
Можно было бы сказать, что группа — это множество с определенной на нем ассоциативной операцией, содержащее нейтральный элемент.
Между прочим, такая структура действительно существует и называется моноидом. Приведенное определение могло бы стать определением группы, но преобразования треугольника обладают еще одним свойством, которое будет интересно обобщить. Это свойство обратимости, согласно которому для любого преобразования всегда найдется другое, которое вернет треугольник в исходное положение. Допустим, мы применили поворот R. Если теперь мы применим R2, получим R2R = R3 = I. Таким образом, преобразование R2 обратно преобразованию R. В других случаях движение может быть обратно самому себе, как, например, симметрии S, RS и SR. Существование обратной операции означает, что для любого элемента а множества G всегда найдется другой элемент b такой, что а * b и b * а будут равны нейтральному элементу.
Часто вместо b записывают а-1. Так определяется группа. Чуть позже мы покажем, что определить группу на множестве {х, у, z) можно единственным способом.
Определение.
Группа — это множество G с определенной на нем операцией *, которая ставит в соответствие любым двум элементам множества G, а и b, третий элемент множества G, а * b такой, что выполняются следующие условия.
1. Операция * является ассоциативной, то есть равенство
(а * b) * с = а * (b * с)
верно для любых а, b и с множества G.
2. На множестве G существует нейтральный элемент е такой, что равенства а*е = е*а = а выполняются для любого элемента а на множестве G.
3. Для любого элемента а множества G можно найти элемент b множества G, который удовлетворяет соотношению a*b = b*a = e.
53
Первая групповая операция, которая приходит в голову, — сложение натуральных чисел. Эта операция обладает свойством ассоциативности, а 0 — ее нейтральный элемент. Но чтобы определить группу, необходимо, чтобы для каждого элемента существовал обратный элемент. Для этого добавим к группе отрицательные числа:
—1 будет обратным элементом для 1, так как 1 + (—1) = (—1) + 1 = 0, аналогично —2 будет обратным элементом для 2 и так далее.
Мы получили группу целых чисел, которая обозначается буквой ? и содержит бесконечно много элементов. Если мы рассмотрим не сложение, а вычитание, то не сможем определить группу: как мы уже показали, вычитание не обладает свойством ассоциативности.
ЛЕВИ-СТРОСС: Вернемся к определению группы. Верно ли, что для любых двух ее элементов а и b а*b и b*а будут совпадать?
ВЕЙЛЬ: Необязательно. Именно поэтому в свойствах 2) и 3) мы записали оба этих равенства. Указать, что а * е должно равняться е, недостаточно, так как е * а совершенно необязательно будет равняться а * е. Если мы укажем, что для двух любых элементов группы выполняется условие a*b = b*a, то исключим из рассмотрения несколько очень интересных примеров. Вы уже видели, что если поменять местами R и S, результат операции изменится. Таким образом, преобразования треугольника не удовлетворяют приведенному выше определению группы. Разумеется, тот факт, что а*b и b*а в общем случае не совпадают, вовсе не означает, что не могут существовать такие а и b, что будет выполняться равенство а * b = b * а.
Если это равенство выполняется всегда, то говорят, что операция обладает коммутативностью. Если групповая операция является коммутативной, то группа называется коммутативной, или абелевой.
ЛЕВИ-СТРОСС: Но почему абелева?
ВЕЙЛЬ: Группы называются абелевыми в честь норвежского математика Нильса Хенрика Абеля (1802—1829), который с помощью теории групп, только-только зарождавшейся в то время, показал, что почти никакое уравнение пятой степени нельзя решить элементарными методами.
Название «абелева группа» ввел Камиль Жордан в своем «Трактате о подстановках и алгебраических уравнениях», изданном в 1870 году. Жордану пришла в голову прекрасная идея — сделать из имени собственного прилагательное, которое можно использовать как полноценное определение.
Похожие названия ввели члены группы Бурбаки: мы говорили не о геометрии Римана или кольце Артина, а о римановой геометрии и артиновом кольце. Когда явное указание на имя автора исчезало, открывались новые смыслы.
ЛЕВИ-СТРОСС: Но разве не Эварист Галуа придумал группы? Кто-то рассказал мне о том, что произошло с Галуа в ночь перед дуэлью.
54
ВЕЙЛЬ: До чего же всем нравится эта история! Я не раз слышал, что Галуа, которому было суждено умереть на следующий день, в порыве вдохновения создал всю свою теорию всего за одну ночь. Галуа первым использовал понятие «группа» в ряде статей, которые можно назвать одними из прекраснейших в истории человечества. Сложно сказать, насколько велико на самом деле было влияние Галуа. Впрочем, группы, которые он изучал, отличались от тех, что рассматриваем мы. Галуа интересовали группы перестановок. Перестановкой на множестве из n элементов называется способ упорядочения элементов множества. На множестве перестановок можно определить групповую операцию. Допустим, мы выбрали перестановки
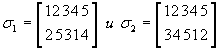
на множестве из пяти элементов {1, 2, 3, 4, 5}. Так мы указываем, что после перестановки ?1 множество примет вид {2, 5, 3, 1, 4}, после перестановки ?2 — {3, 4, 5, 1, 2}. Как видите, под каждым элементом исходного множества записан элемент, который приходит ему на смену после перестановки. Чтобы определить группу перестановок, необходимо описать композицию перестановок. Сейчас я покажу, как это можно сделать. Чтобы определить, чему равен результат ?1 * ?2, сначала посмотрим, какое число записано под элементом 1 в перестановке ?2. Это число 3. Затем посмотрим, какому числу соответствует 3 в перестановке ?1. Это вновь будет 3.
Тогда в композиции ?1 * ?2 числу 1 ставится в соответствие 3. Теперь посмотрим, что произойдет с числом 2: при перестановке ?2 ему на смену придет 4, при перестановке ?1 4 соответствует 1, следовательно, в композиции перестановок ?1 * ?2 числу 2 ставится в соответствие число 1. Продолжив рассуждения, получим
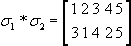
Эта композиция перестановок полностью удовлетворяет всем условиям, приведенным в определении группы. Таким образом, мы получили симметрическую группу Sn, где n — число элементов множества, к которому применяется перестановка.
ЛЕВИ-СТРОСС: А где используются эти группы?
ВЕЙЛЬ: Повсеместно! Между прочим, существует теорема, согласно которой любая конечная группа содержится в некоторой симметрической группе — достаточно верно выбрать число элементов группы. Более того, мы, сами того не осознавая,
55
уже работали с симметрической группой. Помните, как мы различали преобразования треугольника? Мы пронумеровали его вершины и рассмотрели, как они меняются местами при различных движениях. Получается, что преобразование треугольника — не более чем перестановка чисел 1, 2 и 3. К примеру, после поворота R первая вершина будет находиться там, где раньше располагалась вторая, следовательно, при этой перестановке 1 ставится в соответствие 2. Аналогично, вершины 2 и 3 будут находиться там, где раньше располагались 3 и 1 соответственно, таким образом, при этой перестановке 3 соответствует 2, 1—3. Следовательно, поворот R описывается той же информацией, что и
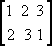
Повторим рассуждения для каждого преобразования и получим следующую таблицу соответствий.
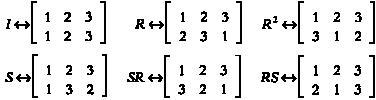
Обратите внимание, что если мы составим композицию перестановок
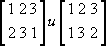
которые, как мы только что показали, обозначают R и S соответственно, то получим следующую перестановку:
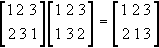
которая соответствует RS. Перестановки и преобразования треугольника в точности соответствуют друг другу! С точки зрения структуры группа преобразований, оставляющих треугольник неизменным, идентична симметрической группе S3 Говорят, что эти две группы изоморфны.
56
В общем случае группы G и Н называются изоморфными, если существует функция f, которая сопоставляет каждому элементу G некий элемент Н так, что выполняются три следующих условия:
1) различным элементам соответствуют различные отображения;
2) любой элемент Н является отображением некоторого элемента G;
3) функция f удовлетворяет определению групповой операции, а именно: если мы выполним операцию над элементами g1 и g2 множества G, после чего найдем отображение ее результата или же если мы сначала найдем отображения f(g1) и f(g2), после чего выполним операцию над ними, то полученные результаты будут одинаковы[5].
ЛЕВИ-СТРОСС: Прекрасно, что дальше?
ВЕЙЛЬ: Аксиомы, определяющие структуру группы, можно использовать при доказательстве теорем, которые будут верны для любых групп при соблюдении необходимых условий. В частности, эти теоремы будут верны для нашей группы преобразований треугольника! Пункт 2 определения группы гласит, что существует нейтральный элемент е такой, что равенство а*е = е*а = а верно для любого а, и в определении не указывается, сколько элементов группы обладают этим свойством. Но в пункте 3 определения подразумевается, что он единственный — в противном случае потребовалось бы уточнить, какому из нейтральных элементов равна композиция произвольного элемента и обратного ему. Докажем, что нейтральный элемент является единственным. Допустим, что существуют два нейтральных элемента, е1 и е2. Требуется доказать, что е1 = е2. Рассмотрим произведение е1 * е2.
С одной стороны, е1 — нейтральный элемент, поэтому он не изменяет значение элемента, записанного слева от него. Следовательно, е1 * е2 = е2. С другой стороны, е2 — также нейтральный элемент, следовательно, при умножении любого элемента на е2 этот элемент не изменится. Таким образом, е1 * е2 = е1 Мы доказали, что е1 * е2 одновременно равняется е1 и е2, следовательно, е1 и е2 должны быть равны.
Единственность нейтрального элемента. В любой группе существует только один элемент, для которого выполняется равенство а*е = е*а = а для любого а на множестве G.
ЛЕВИ-СТРОСС: Обратные элементы также будут единственными?
57
ВЕЙЛЬ: Конечно! Как и раньше, предположим, что существует два элемента b1 и b2 такие, что а*b1 = b1*а = е и а*b2 = b2*а = е. Получим, что а * b1 = а * b2 так как обе части равенства в свою очередь равны е. Это равенство по-прежнему будет корректным, если мы умножим обе его части на b1 Получим
b1 * а * b1 = b1 * а * b2
Напомню, что в произведении трех элементов скобки можно расставить как угодно. Так,
b1 * а * b1 = (b1 * а) * b1 = е * b1 = b1
поскольку b1* а = е, где е — нейтральный элемент. Аналогично,
b1 * а * b2 = (b1 * а) * b2 =e*b2 = b2
Так как оба выражения равны, имеем: b1 = b2 В силу этого свойства элемент b можно считать обратным а и записать b = а-1
Я очень рад, что вы задали этот вопрос, поскольку при ответе я упомянул одно утверждение, которое нам очень пригодится в будущем. Обратите внимание, что из равенства а * b1 = а * b2 мы вывели, что b1 = b2 Это свойство общее для всех групп: если результаты умножения двух элементов на третий элемент (в том же порядке) совпадают, то два исходных элемента равны.
Закон сокращения. Если в группе G выполняется одно из равенств
а * b = а * с или b * а = с * а, то b = с.
ЛЕВИ-СТРОСС: Но как это доказать?
ВЕЙЛЬ: Очень просто: достаточно повторить действия, которые мы уже выполнили. Допустим, дано равенство а * b = а * с. Согласно аксиоме теории групп под номером 3 для элемента а существует обратный элемент, который к тому же будет единственным. Обозначим его через a-1. Равенство по-прежнему будет верным, если мы припишем в каждую его часть слева a-1. Имеем:
a-1 * а * b = a-1 * а * с.
Теперь можно использовать свойство ассоциативности и сгруппировать элемент а и обратный ему. Так как a-1 * а равно е, то, с одной стороны,
а-1 * а * b = = (a-1 * а) * b = е * b = b,
с другой стороны,
a-1*а*с = (a-1*а)*с = е*с = с,
поэтому обязательно будет выполняться соотношение b = с. Если исходное равенство будет записано не в виде a*b = a*c, а в виде b * а = с * а, достаточно будет провести аналогичные рассуждения, но приписать обратный элемент не слева, а справа.
58
ЛЕВИ-СТРОСС: А для чего нужно это свойство?
ВЕЙЛЬ: Оно, в частности, позволяет доказать, что таблица умножения конечной группы — это латинский квадрат. Напомню: латинский квадрат — это таблица чисел, в каждой строке и в каждом столбце которой записаны все элементы группы.
Обозначим их через а1 а2... аn. Приведем доказательство для второго столбца таблицы; для любого другого столбца оно будет аналогичным. Какие элементы записаны во втором столбце? Те, что определяются умножением а2 на все элементы группы, то есть а2 * а1, а2 * a2, а2 * а3 ... и так далее до а2 * аn. Допустим, что два выражения из этого списка равны, то есть существуют два индекса j и k такие, что а2 * аj = а2 * ak. Так как а2 приводится в обеих частях выражения, по закону сокращения имеем аj = ak. Таким образом, в этом столбце нет двух одинаковых элементов!
Но так как группа состоит из n элементов, а в столбце таблицы нужно записать n неповторяющихся элементов, то в этом столбце будут записаны все элементы группы! Понимаете?
ЛЕВИ-СТРОСС: Для строк это свойство доказывается аналогично — достаточно поменять множители местами.
ВЕЙЛЬ: Вы определенно делаете успехи, господин Леви-Стросс. Мне кажется, вы готовы ко встрече с новыми группами. Помните, совсем недавно я говорил, что групповая операция на множестве из трех элементов определяется единственным образом? Теперь я объясню, почему это так, но прежде чем изучить случай с тремя элементами, рассмотрим группы порядка 1 и 2. Я уже объяснял, что такое порядок группы? По-моему, нет. Для конечных групп порядком называется число элементов группы.
ЛЕВИ-СТРОСС: Но мы уже дали порядку другое определение, не так ли?
ВЕЙЛЬ: И да, и нет. В примере с преобразованиями треугольника я говорил, что R имеет порядок, равный трем, так как три поворота фигуры на 120°, выполненные последовательно, не изменяют ее. В общем случае порядок элемента равен n, если, выполнив операцию над этим элементом n раз (или возведя его в степень n), мы получим тождество. Вам может показаться, что это определение не имеет ничего общего с предыдущим, но сейчас я продемонстрирую, что это не так.
Рассмотрим произвольный элемент группы, например а. Мы можем составить группу степеней а, то есть <а> = {а, а2, а3...}, где а2 — сокращенное обозначение а * а, а3 обозначает а * а * а и так далее. Допустим, что а имеет порядок n в соответствии с первым определением, то есть аn — нейтральный элемент группы. Тогда перечень степеней остановится на аn = е и затем начнется сначала, так как
аn+1 = аn * а = е*а = а, аn+2 = а2
и так далее. На самом деле множество будет содержать
59
всего n элементов: <а> = {а, а2 ... аn = е}. И это непростое множество: <а>, в свою очередь, является группой: оно содержит нейтральный элемент, результат операции над двумя степенями а всегда равен степени а, и элемент аn-i является обратным для аi. Следовательно, порядок элемента — это порядок множества, состоящего из его степеней. Это новое определение носит более общий характер, чем первое.
Впрочем, интереснее другое. Я предлагаю вам поупражняться в различных действиях над группами и посмотреть, как выглядят группы наименьшего порядка.
В определении группы мы указали, что она обязательно должна содержать нейтральный элемент, поэтому группа не может быть пустой — она всегда будет содержать как минимум нейтральный элемент. Если порядок группы равен единице, она не может содержать других элементов, поэтому будет выглядеть так: G = {е}. Посмотрим, как выглядят группы из двух элементов. Они должны иметь вид G = {е, а}, где е — нейтральный элемент, а — другой элемент, отличный от е. По определению, а*е = е*а = а, а также е * е = е. Следовательно, чтобы полностью определить эту группу, достаточно найти значение а2 = а * а. Этот элемент также должен принадлежать группе, поэтому у нас есть всего два варианта: либо а2 = е, либо а2 = а.
Последний вариант можно сразу же исключить из рассмотрения: применив закон сокращения к равенству а2 = а, получим, что а = е, но мы уже отмечали, что а и е отличаются. Следовательно, существует всего одна группа второго порядка.

Группа второго порядка.
ЛЕВИ-СТРОСС: Я кое-что не понял: почему существует всего одна группа второго порядка? Ведь я могу заменить элемент а чем угодно.
ВЕЙЛЬ: Но таблица умножения не изменится. Важно не то, как выглядят элементы множества, а то, как они связаны между собой. Вспомните вашу историю с одуванчиком. Перестановки множества {1, 2, 3} не имеют ничего общего с преобразованиями, которые оставляют треугольник неизменным, но, как мы уже говорили, элементы обоих множеств можно объединить в пары так, что групповая операция будет корректной. С точки зрения структуры две эти группы будут неразличимы, изоморфны. Они подобны двум различным воплощениям одной и той же идеи
60
Платона — группы шестого порядка, отношения между элементами которой приведены в таблице. Понимаете?
ЛЕВИ-СТРОСС: Следовательно, существует всего одна «идея Платона» о группе третьего порядка?
ВЕЙЛЬ: Да, всего одна.
ЛЕВИ-СТРОСС: Дайте мне попробовать. Группа третьего порядка содержит е и два других элемента а и b, все ее элементы различны: G = {е, а, b}. Нам известно, что элементы группы связаны следующими отношениями: е * е = е, е*а = а*е = а и е*b = b*е = b. Попробуем вычислить значение а2. Так как это элемент группы, допустимы всего три варианта: a2 = е, a2 = а и a2 = b. Тем не менее мы вновь можем исключить из рассмотрения а2 = а — в этом случае по закону сокращения элемент а будет равен нейтральному элементу. Остается два варианта: а2 = е и а2 = b. Но это означает, что существуют две разновидности групп третьего порядка!
ВЕЙЛЬ: Ваши рассуждения следует немного уточнить. Допустим, что а2 = е.
Тогда таблица, описывающая эту группу, будет начинаться так:

Мы уже доказали, что таблица умножения группы — это латинский квадрат, поэтому в каждом столбце и каждой строке таблицы должны быть записаны все элементы группы. Во второй строке уже записаны а и е, следовательно, в третьей ячейке этой строки может находиться только b, но тогда в третьем столбце b будет записано дважды. Эту таблицу нельзя дополнить так, чтобы в каждой строке и в каждом столбце были записаны все элементы группы. Следовательно, таблица не может описывать группу, и вариант a2 = е исключен.
ЛЕВИ-СТРОСС: Таким образом, остается всего один вариант: a2 = b. Очень интересно! Следовательно, мы можем записать группу так: G = {е, а, a2}. Верно?
ВЕЙЛЬ: Осталось указать, каким будет результат операции над а и a2, то есть каким будет значение a3. Найти его очень просто: так как элемент a3 принадлежит группе, он может равняться только е, а или a2. Тем не менее, если бы a3 был равен одному из двух последних элементов, то, применив закон сокращения один или два
61
раза, мы получили бы, что a3 — нейтральный элемент. Поскольку это не так, у нас остается единственный вариант: а3 = е. Все группы третьего порядка изоморфны.

Эту группу мы уже видели в нашем примере с преобразованиями треугольника. Если вы внимательно посмотрите на составленную нами таблицу умножения, то увидите, что ее часть полностью совпадает с группой третьего порядка. Иногда внутри групп содержатся другие, более мелкие группы, образованные частью элементов исходной группы. Они называются подгруппами.
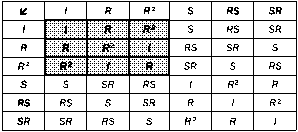
Подгруппа третьего порядка.
Такие группы, образованные степенями одного и того же элемента, называются циклическими, а сам элемент называется порождающим. Для произвольной группы G семейство порождающих элементов — это конечное множество элементов группы, на основе которых можно получить все остальные ее элементы. К примеру, поворот R и симметрия S — порождающие элементы группы преобразований треугольника. Чтобы лучше понять, что такое циклические группы, представьте себе циферблат часов. Каждые 12 часов стрелка вновь возвращается в исходное положение, поэтому при взгляде на часы нельзя определить, прошло какое-то время или нет.
Если выборы заканчиваются в 9 часов вечера, а подсчет голосов длится четыре часа, то никому не придет в голову сказать, что результаты будут известны в 21 + 4 = 25 часов.
Вместо этого по достижении 24 часов нужно начать отсчет снова и добавить оставшийся час. Таким образом, итоги голосования будут известны в час ночи.
62
Существуют часы с циферблатами, разделенными на 12 и 24 деления, но ничто не мешает изготовить часы с произвольным числом делений, например n. Базовым множеством группы будет множество натуральных чисел, меньших n. Мы запишем эти числа в квадратных скобках, чтобы указать, что каждое из них в действительности обозначает несколько «часов» одновременно: [0], [1], [2] ... [n - 1].
Мне хотелось бы сказать, что операцией, определенной над двумя элементами множества, будет привычная нам операция сложения без квадратных скобок, однако в этом случае мы столкнемся с серьезной проблемой. Представьте, что n равно, например, 5. Тогда представленное выше множество будет иметь вид: [0], [1], [2], [3], [4]. Сумма элементов 3 и 4 будет равна 3 + 4 = 7, а это число не принадлежит множеству. Необходимо видоизменить операцию сложения. Будем обнулять счетчик всякий раз, достигая 5. В нашем примере с числами 3 + 2 = 5, после чего наступает следующий «день», и к полученному результату нужно добавить еще две единицы. Таким образом, [3] + [4] = [2]. Изменять некоторые другие суммы не потребуется: к примеру, 1 + 2 = 3, 3 меньше 5, следовательно, [1] + [2] = [3]. Тем не менее [2] + [3] = [0], а [2] + [4] = [1], так как из результата нужно вычесть 5.
Получим следующую таблицу.
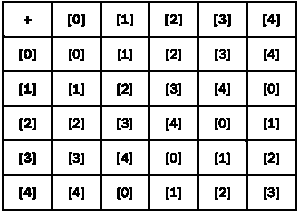
Для любого числа n можно доказать, что эта видоизмененная операция сложения будет групповой операцией на множестве {[0], [1], [2] ...[n — 1]}. Это циклическая группа порядка n, или группа целых чисел со сложением по модулю n. Она обозначается Z/n.
ЛЕВИ-СТРОСС: Достаточно, господин Вейль. Настало время поговорить о браке!
63
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
Пока алгебра не разлучит нас Теория групп и ее применение
Пока алгебра не разлучит нас Теория групп и ее применение Хавьер ФресанМир МАТЕМАТИКИ 35Москва - 2014 О, сколько всего я говорил ему, не боясь наказанья судьбы, любви, времени и смерти! Франсиско де Альдана Она читает Вергилия, Папу Римского и алгебру так, как читают
История вопроса
История вопроса Хорошо известно, что от начала «нашей эры» («новой эры») не велось непрерывного счета лет — от первого года до, скажем, 2002 года. Первый год «новой эры» был вычислен гораздо позже как год Рождества Христа. Считается, что впервые этот год вычислил римский
§ 1. История
§ 1. История Теория чисел — это ветвь математики, имеющая дело с целыми положительными числами1, 2, 3…,которые также называют натуральными числами.Археология и история учат нас, что человек рано начал считать. Сначала он научился складывать числа, потом, много позже,
1. История первая
1. История первая Дорогая, напекла бы ты нам своих вкусных пирожков, — обратился Червонный Король к Королеве в один погожий летний денек. — Что толку печь пирожки без повидла?! — с неожиданной яростью завопила Королева. — Ведь самое вкусное в пирожках — это повидло!!— Так
2. История вторая
2. История вторая — Что ж, украденное повидло мы отыскали, — сказал Король, — теперь ты можешь испечь пирожков.— А как, по-твоему, я должна печь пирожки без муки? — спросила Королева.— Постой, уж не хочешь ли ты сказать, что и муку украли?! — вскричал Король.— Вот именно! —
3. История третья
3. История третья — Вот твоя мука, — с удовлетворением произнес Король, — теперь-то ничто не помешает тебе испечь пирожки.— Испечь пирожки? Без перца? — спросила Королева.— Без перца? — недоуменно переспросил Король. — Ты что же, печешь пирожки с перцем?— А как же, —
7. История четвертая
7. История четвертая — Ну и пришлось же мне попотеть, разыскивая твой дурацкий перец, — сердито бурчал Король, — и главное, что в нем проку, в этом перце! Как будто без него пирожков не настряпать! И ведь дался тебе этот перец! — продолжал ворчать он. — Ты бы еще промокашку в
8. История пятая
8. История пятая — Отлично, — обрадовался Король, — вот твой сахар, так что теперь ничто не помешает тебе настряпать мне пирожков.— Как, без соли? — спросила Королева.Нет, вы только подумайте! Соль тоже украли! На этот раз преступника искали среди троих подозреваемых:
9. История шестая
9. История шестая — Вот тебе еще немного соли, теперь-то ты можешь приступить к стряпне, — сказал Король.— А вот и не могу, — возразила Королева. — Кто-то украл мой противень.— Как, и противень! — расстроился Король. — Как ни крути, а нам придется его отыскать!В результате
10. История седьмая
10. История седьмая — Получи свой противень в целости и сохранности, — сказал Король, — и напеки же, наконец, пирожков.— Без рецепта не могу, — сказала Королева.— Воспользуйся своим обычным рецептом, — вскричал Король, теряя остатки терпения. — В прошлый раз твои пирожки
12. История восьмая
12. История восьмая — Послушай, теперь поваренная книга снова у тебя, — сказал Король, — а значит, и рецепт на месте. Испеки же, наконец, пирожки!— Без молока, масла и яиц?— О нет! — застонал Король. — Мне этого уже не вынести!— Зато теперь я точно знаю, что это дело рук
13. Последняя история
13. Последняя история — Итак, вот масло, яйца и молоко, — сказал Король. — Повидло, мука, сахар, соль, противень и поваренная книга у тебя тоже есть, и даже перец, будь он неладен. Уж теперь-то ничто не мешает тебе испечь пирожков!И вправду, Королева настряпала пирожков, и