Глава 5 Под знаком Диофанта
Глава 5 Под знаком Диофанта
Фурье считал, что главная цель математики есть принесение пользы обществу и объяснение явлений природы; тем не менее такой философ, как вы, должен знать, что единственной целью науки является честь человеческого разума, и с этой точки зрения вопрос о числе так же важен, как и вопрос о системе мира.
Карл Густав Якоб Якоби в письме к Адриену Мари Лежандру
ЛЕВИ-СТРОСС: Помните, как в одной из наших бесед вы пообещали мне подробнее рассказать о задаче из вашей докторской диссертации?
ВЕЙЛЬ: Как я мог забыть об этом! Но в этот раз, если вы позволите, мы применим иной метод. Я написал несколько достаточно подробных заметок; прочитайте их, а затем спросите меня о том, что показалось вам непонятным. Вперед!
О жизни математика Диофанта Александрийского достоверно практически ничего не известно. Мы точно знаем лишь возраст мудреца из эпиграммы-задачи, записанной на его надгробии и приведенной в Палатинской антологии:
«Прах Диофанта гробница покоит; дивись ей и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком.
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругой он обручился.
С нею, пять лет проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей».
Если мы обозначим через х число лет, прожитых Диофантом, то получим следующее уравнение первой степени:
х = x/6+ x/12+x/7+5+x/2+4.
87
Выполнив несколько элементарных преобразований, получим, что Диофант прожил 84 года. Это уравнение намного проще, чем те, что обеспечили александрийскому мудрецу место в истории математики. В «Арифметике» Диофант впервые рассмотрел целые корни полиномиальных уравнений, которые сегодня в его честь называются диофантовыми. К диофантовым относится, например, уравнение
хn + уn = zn.
Если показатель степени равен 2, это уравнение имеет бесконечно много положительных решений, но если n больше либо равно 3, уравнение решений не имеет. Первым на это обратил внимание француз Пьер Ферма, когда изучал «Арифметику» Диофанта.
На страницах книги Ферма написал: «Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него». Первое доказательство этой теоремы, названной великой теоремой Ферма, было получено лишь три с половиной столетия спустя. В этом доказательстве использовались намного более сложные методы, чем те, что были известны французскому математику. Несмотря на кажущуюся простоту, диофантовы уравнения принадлежат к числу труднейших задач математики, поэтому мы рассмотрим лишь простейшие из них: линейные уравнения, уравнение Пелля — Ферма и уравнения эллиптических кривых.
Введение
Прежде чем приступить к изучению диофантовых уравнений, проясним некоторые понятия. Так как в моих заметках упоминаются различные классы чисел, скажем о них несколько слов. С одной стороны, существуют натуральные числа, которые используются при счете: 1, 2, 3... (к ним также иногда относят ноль). Для двух любых натуральных чисел определена операция сложения, однако она не может быть групповой: чтобы существовали обратные элементы, необходимо также рассмотреть отрицательные числа. Добавив отрицательные числа к натуральным, получим абелеву группу целых чисел: 0, 1,-1, 2,-2, 3,-3. В действительности на этой структуре определена не одна, а сразу две операции: мы можем не только складывать целые числа, но и перемножать их. Операция умножения ненулевых целых чисел также не является групповой. Так, чтобы, к примеру, элемент 2 имел обратный, необходимо рассмотреть число 1/2. Чтобы устранить этот недостаток, необходимо рассмотреть все дроби вида а/b (где а и b целые числа, b отлично от нуля), которые образуют множество рациональных чисел. Каждому из них мы можем поставить в соответствие периодическую десятичную дробь: к примеру, для 1/3 такой дробью будет 0,3333..., для 2/11 — 0,181818... Если мы будем рассматривать только периодические дроби, то такие простые уравнения, как х2 = 2, не будут иметь решения, поскольку десятичная запись квадратного корня из 2 — непериодическая дробь.
88
Такие числа называются иррациональными. Чтобы получить еще больше решений, мы можем рассмотреть все десятичные дроби, в записи которых отсутствуют какиелибо закономерности. Такие числа называются вещественными.
Но вернемся к натуральным числам, которые Кронекер называл божьим творением. Для двух натуральных чисел m и n, m называется делителем n, если результат деления n на m — натуральное число. К примеру, 2 — делитель 10, так как 10 при делении на 2 дает 5 — натуральное число; 2 не является делителем 15, так как 15 при делении на 2 дает 7,5 — «некруглое» число. Если n делится на m, то существует натуральное число k такое, что n будет произведением m и k: n = m · k. Обратите внимание, что делители числа всегда меньше либо равны ему, и любое число делится на единицу и само себя. В некоторых случаях число делится только на единицу и само себя — такие числа называются простыми. Так, 5 — простое число, так как ни 2, ни 3, ни 4 не являются его делителями, а 6 не является простым, так как делится на 2 и на 3. Первые простые числа — 2, 3, 5, 7, 11, 13, 17, 19, 23... Можно доказать, что простых чисел бесконечно много.
Простые числа составляют основу всей арифметики: через них определяются все остальные числа. В самом деле, если n не является простым, то на интервале от 1 до n найдется натуральное число, которое будет его делителем. Таким образом, n можно представить в виде n = а · b. К примеру, если исходное число равно 30, имеем 30 = 2 · 15. Мы получили два числа а и b, для которых можем повторить описанные действия еще раз. Если оба этих числа простые, процесс заканчивается.
Если же какое-то из этих чисел не является простым, мы вновь запишем его в виде произведения двух множителей. В нашем примере 2 является простым, а 15 можно представить как произведение 3 и 5. Имеем 30 = 2 · 3 * 5. Так как 2, 3 и 5 — простые числа, процесс завершен. В общем случае на каждом шаге мы либо находим простой сомножитель, либо представляем число как произведение двух меньших чисел, поэтому описанный нами процесс рано или поздно обязательно завершится.
Основная теорема арифметики: любое натуральное число можно представить в виде произведения простых множителей.
Хотя доказать основную теорему арифметики нетрудно, задача о разложении числа на простые множители на практике может оказаться неразрешимой.
89
К примеру, если n представляет собой произведение двух простых чисел р и q приблизительно из 400 знаков каждое, то для разложения n на простые множители даже самым мощным компьютерам потребуется время, сравнимое с возрастом Вселенной. Как вы увидите далее, это один из основных принципов криптографического алгоритма RSA, обеспечивающего безопасность всех наших компьютерных транзакций.
Введем новое понятие: для двух натуральных чисел m и n будем называть наибольшим общим делителем наибольшее натуральное число, на которое делятся одновременно m и n. Обозначим его НОД (m, n). Если нам известны разложения m и n на простые множители, найти НОД очень просто: нужно взять простые числа, которые содержатся в обоих разложениях, возведенные в наименьшую степень. Допустим, что мы хотим найти НОД 50 = 2 · 5? и 120 = 23 · 3 · 5. Общие делители этих чисел — 2 и 5. В первом случае они возведены в степени 3 и 1, во втором — в степени 1 и 2.
Таким образом, НОД будет равен 21 · 51 = 10. Задача о разложении числа на простые множители на практике оказывается неразрешимой, поэтому для очень больших m и n описанный метод неприменим. К счастью, существует еще один метод расчета наибольшего общего делителя, который называется алгоритмом Евклида. Допустим, что m больше n. На первом шаге разделим m на n. Возможны два случая: если остаток от деления равен 0, то n — делитель m, следовательно, n — искомый НОД. В противном случае повторим деление, заменив m на n, а n — на остаток от деления r. Можно доказать, что наибольший общий делитель m и n совпадает с наибольшим общим делителем n и r[8].
Вернемся к нашему примеру: остаток от деления 120 на 50 равен 20, следовательно, на следующем шаге алгоритм нужно повторить для 50 и 20. Остаток от деления 50 на 20 равен 10, поэтому на следующем шаге рассмотрим 20 и 10. На этот раз первое число делится на второе без остатка, таким образом, НОД равен 10. Более того, алгоритм Евклида позволяет получить некоторую дополнительную информацию: если мы рассмотрим последний ненулевой остаток от деления, то сможем записать 10 = 50 — 2·20. Сделаем еще один шаг назад и получим, что 20 = 120 — 2 · 50. Если теперь мы подставим это выражение в первое равенство, то получим отношение с целыми коэффициентами, связывающее
10 = 50-2-(120-2·50) = 5·50-2·120.
90
В общем случае алгоритм Евклида позволяет не только эффективно вычислить наибольший общий делитель чисел, но также показать следующее:
Предложение. Пусть m и n — два натуральных числа. Обозначим их наибольший общий делитель через d. Тогда существуют два целых числа u и v такие, что d = mu + nv.
Особенно интересен случай, когда m и n не имеют общих делителей. Тогда их наибольший общий делитель равен 1, а m и n называются взаимно простыми. Согласно приведенному выше предложению, существуют два целых числа u и v такие, что mu + nv = 1. Это соотношение называется соотношением Безу.
Еще одно фундаментальное свойство делимости чисел звучит так: если число а — делитель произведения bс, и нам известно, что а и b — взаимно простые, то а обязательно будет делителем с. В самом деле, в противном случае один из простых делителей а также будет делителем b, и эти числа не будут взаимно простыми.
С другой стороны, если d — наибольший общий делитель а и b, то существуют два целых числа р и q такие, что а = dp, b = dq. Это утверждение выполняется для любых общих делителей, но так как d — НОД, можно утверждать, что р и q взаимно простые — в противном случае а и b имели бы общий делитель, больший d.
Линейные уравнения
Теперь мы знаем все, что нужно для решения диофантовых уравнений вида ах + by = с,
где а, b и c — произвольные целые числа. Чтобы решить это уравнение, нужно найти все пары целых чисел (х, у), которые удовлетворяют соотношению ах + by = с.
Посмотрим, как это сделать. Обозначим через d наибольший общий делитель а и b. По определению а и b делятся на d, следовательно, выражение ах + by также будет делиться на d. Так как согласно исходному уравнению ах + by = с, число d также должно быть делителем с. Следовательно, если с не делится на d, то уравнение не имеет решений. Так, решений не имеет уравнение 50х + 120у = 7. Мы уже показали, что наибольший общий делитель 50 и 120 равен 10, а 7 не делится на 10.
Далее будем предполагать, что с делится на d.
Тогда мы можем записать а = dp, b = dq и с = dr, где р и q — взаимно простые.
Сначала рассмотрим случай с = 0, то есть однородное уравнение ах + by = 0.
91
Разделив на d первый член уравнения, получим следующее: достаточно решить уравнение рх + qy = 0, или, что аналогично, рх = —qy. Будем рассуждать следующим образом: так как рх равно — qy, qy должно делиться на р. Однако р и q взаимно простые, следовательно, остается единственный вариант: у делится на р, то есть существует целое число ? такое, что у = ?р. Аналогично доказывается, что х делится на q, поэтому существует другое целое число ? такое, что х = ?q. Подставив значения х и у в уравнение, получим: ?pq = —?pq, то есть ? = —?, так как pq отлично от нуля. Следовательно, решениями уравнения ах + by = 0 будет пара чисел (q, —р) и всех кратных им чисел (?q, —?р).
Теперь предположим, что с отлично от нуля. Если известно два решения (x0, у0) и (х1 y1) уравнения ах + by = с, то:
а(х0 - х1) + b(у0 - у1) = (ах0 + by1-(ax1+by1) = с-с = О,
откуда следует, что (x0 — x1, у0 — y1) — решение однородного уравнения ах + by = 0.
Так как все решения этого уравнения имеют вид (?q, —?р), найдется целое число ? такое, что x0 — x1 = ?q и у0 — у1 = —?р, или, что аналогично, х = x0 — ?q и y1 = y0 +?р. Иными словами, уравнение имеет бесконечно много решений, но все они выводятся из частного решения (x0, у0). Напомню, что р и q — результат деления а и b на наибольший общий делитель. Следовательно, мы доказали, что все решения выглядят так:
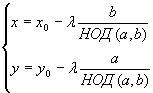
где (x0, у0) — частное решение, ? — любое целое число. Теперь всего лишь осталось найти метод, позволяющий получить (x0, у0). Найти эти решения нетрудно, если р и q — взаимно простые, так как по соотношению Безу существуют два целых числа u и v такие, что рu + qv— 1. Умножив u и v на r, получим два числа x0 = ur и у0 = vr такие, что ax0 + by0 = с.
Рассмотрим пример. Допустим, мы хотим решить диофантово уравнение 50х + 120у = 20.
Мы уже знаем, что наибольший общий делитель 50 и 120 равен 10.
Так как 20 делится на 10, уравнение имеет решение.
92
В этом случае в упрощенном виде уравнение выглядит так: 5х + 12у = 2. Найдем числа, которые мы обозначили через u и v. Так как 1 = 5 — 2 ·2 и 2 = 12 — 2·5, имеем
1 = 5 - 2 · (12 - 2 · 5) = 5 · 5 - 2 · 12,
то есть u = 5, v = —2. Умножив эти значения на 2, получим частное решение (10, —4), на основе которого можно найти общее решение:
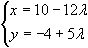
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
Глава 7 Запоминающаяся глава для запоминания чисел[9]
Глава 7 Запоминающаяся глава для запоминания чисел[9] Наиболее часто мне задают вопрос о моей памяти. Нет, сразу скажу я вам, она у меня не феноменальная. Скорее, я применяю систему мнемотехники, которая может быть изучена любым человеком и описана на следующих страницах.
Глава 1
Глава 1 Кто Джон? Для того чтобы узнать, кого из двух братьев-близнецов зовут Джон, нужно спросить одного из них: «Джон говорит правду?». Если в ответ на этот вопрос последует «да», то независимо от того, лжет ли спрошенный близнец или говорит всегда только правду, он должен
Глава 2
Глава 2 1. История первая. По существу, Болванщик заявил, что варенье украли либо Мартовский Заяц, либо Соня. Если Болванщик солгал, то ни Мартовский Заяц, ни Соня не украли варенье. Но тогда Мартовский Заяц, поскольку он не украл варенье, дал правдивые показания.
Глава 3
Глава 3 14. Гусеница и Ящерка Билль. Гусеница считает, что и она, и Ящерка Билль не в своем уме. Если бы Гусеница была в здравом уме, то мнение о том, что и она, и Ящерка Билль не в своем уме, было бы ложно. Следовательно, Гусеница (будучи в здравом уме) не могла бы придерживаться
Глава 4
Глава 4 26. Сколько кренделей у каждого? Назовем одной порцией все крендельки, которые достались Соне, сколько бы их ни было. Тогда Соне досталась 1 порция. Мартовскому Зайцу досталось вдвое больше крендельков, чем Соне (потому что Соню Болванщик посадил на такое место, где
Глава 5
Глава 5 42. Появление первого шпиона. С заведомо не может быть рыцарем, так как ни один рыцарь не стал бы лгать и утверждать, будто он шпион. Следовательно, С либо лжец, либо шпион. Предположим, что С шпион. Тогда показание А ложно, значит, А шпион (А не может быть шпионом, так
Глава 6
Глава 6 52. Первый вопрос. Алиса ошиблась, записав одиннадцать тысяч одиннадцать сотен и одиннадцать как 11111, что неверно! Число 11111 – это одиннадцать тысяч одна сотня и одиннадцать! Для того чтобы понять, как правильно записать делимое, сложим одиннадцать тысяч,
Глава 7
Глава 7 64. Первый раунд (Красное н черное). Если внезапно заговоривший братец сказал правду, то его звали бы Траляля и в кармане у него была бы черная карта. Но тот, у кого в кармане карта черной масти, не может говорить правду. Следовательно, он лжет. Значит, в кармане у него
Глава 9
Глава 9 Во всех решениях этой главы А означает первого подсудимого, В – второго и С – третьего.78. Кто виновен? Из условий задачи известно, что виновный дал ложные показания. Если бы В был виновен, то он сказал бы правду, когда признал виновным себя. Следовательно, В не может
Глава 11
Глава 11 88. Всего лишь один вопрос. Действительно следуют. Рассмотрим сначала утверждение 1. Предположим, некто убежден, что он бодрствует. В действительности он либо бодрствует, либо не бодрствует. Предположим, что он бодрствует. Тогда его убеждение правильно, но всякий,
Глава 1
Глава 1 graphics46 Кто Джон?Чтобы узнать, кто из двух братьев Джон, спросите одного из них: «Джон правдив?» Если он ответит «да», это должен быть Джон, независимо от того, солгал он или сказал правду. Если же он ответит «нет», значит, он не Джон. И вот как это подтверждается.Ответив
Глава 2
Глава 2 graphics48 1. История перваяШляпник заявил, по существу, что повидло украл либо Мартовский Заяц, либо Соня. Если Шляпник солгал, значит ни Мартовский Заяц, ни Соня повидла не крали. Раз Мартовский Заяц кражи не совершал, то он, следовательно, сказал на суде правду.
Глава 3
Глава 3 graphics50 14. Гусеница и Ящерка БилльГусеница убеждена в том, что и она, и Ящерка Билль оба не в своем уме. Если бы Гусеница была в своем уме, то ее суждение о том, что оба они из ума выжили, было бы ложным. Раз так, то Гусеница (будучи в своем уме) вряд ли всерьез могла быть
Глава 4
Глава 4 26. Сколько пирожков?Сколько бы пирожков ни оказалось у Сони, назовем это количество одна порция. Итак, у Сони одна порция пирожков. У Мартовского Зайца вдвое больше пирожков, чем у Сони (в условиях задачи говорится, что Соня получила лишь половину того, что досталось