Глава 2. Поиск

Глава 2. Поиск

Как создаются новые лекарства? Еще совсем недавно фармацевты готовили медикаменты вручную, а их единственными помощниками были бумага и карандаш.

Они создавали и оптимизировали химическую структуру лекарства и в специальных лабораториях синтезировали и испытывали все новые и новые их версии, чтобы подтвердить, действительно ли возросла эффективность таблеток. Этот метод проб и ошибок отчасти объясняет, почему стоимость разработки нового лекарства в среднем составляет 1 млрд долларов.

При создании нового средства, как правило, синтезируется новая молекула, взаимодействующая с неким белком и в конечном итоге нейтрализующая его действие.

В живых организмах белки участвуют в метаболическом каскаде — последовательности реакций. Следовательно, если молекула нейтрализует действие одного из белков, участвующих в интересующей нас последовательности реакций, каскад будет нарушен, а молекула станет хорошим лекарством.

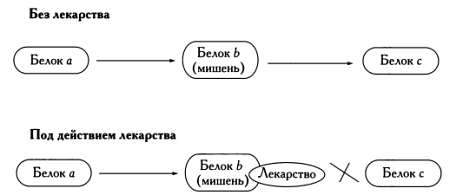
В этом упрощенном сценарии лекарство препятствует взаимодействию белка-мишени с белком с и нарушает метаболический каскад.

Чтобы нейтрализовать один из этих белков, необходимо, чтобы молекулы лекарства соединялись с ним определенным образом. Следовательно, большая часть усилий при создании нового медикамента направлена на то, чтобы новая молекула присоединялась к активному центру нужного белка — мишени.

Чтобы определить, действительно ли молекула лекарства соединяется с молекулой белка, необходимо измерить энергию их взаимодействия. Энергия взаимодействия между молекулой-кандидатом и белком-мишенью — это энергия, которую необходимо приложить для сохранения связи в системе. К примеру, если мы хотим, чтобы магнит держался на двери холодильника, нам не нужно постоянно прикладывать какую-то силу. Достаточно мощный магнит, только поднеси его к дверце, сам по себе притянется к ней с определенной силой. В этом случае говорят: для того чтобы магнит оставался прикрепленным к дверце холодильника, требуется приложить отрицательную энергию.

Разумеется, молекула лекарства, которая не образует связи с молекулой белка-мишени, не окажет лечебного воздействия: такая молекула будет свободно перемещаться по кровеносной системе или тканям, никак не решая задачу нейтрализации белка. А хорошим лекарством будет соединение, для которого энергия взаимодействия будет отрицательной и минимально возможной, — это говорит нам о том, насколько сильно притягиваются молекулы лекарства и белка. Следовательно, основной параметр, значение которого следует оптимизировать при разработке нового лекарства, это энергия взаимодействия.

Подобные задачи, решение которых заключается в определении ряда оптимальных параметров (например, какой шахматной фигурой нужно сделать ход, чтобы выиграть партию, или какими должны быть положение и размеры балок моста, чтобы снизить стоимость строительства и повысить прочность конструкции), объединяются в категорию задач поиска. При этом часто требуется найти параметры, обеспечивающие максимальное значение некой математической функции. В этом случае поиск называется оптимизацией.

Об этом говорил еще Дарвин

Чаще других для решения задач поиска применяется метод эволюционных вычислений. При этом происходит оптимизация значений функций различной сложности, подобно тому как живые организмы эволюционируют, чтобы повысить выживаемость в окружающей среде.

Идею эволюционных вычислений предложил исследователь Джон Холланд в 1975 году в своей книге «Адаптация в естественных и искусственных системах» (Adaptation in Natural and Artificial Systems). Позднее западные ученые обнаружили, что немецкие инженеры уже использовали подобные стратегии для оптимизации формы сопл первых реактивных двигателей самолетов во время Второй мировой войны. Эволюционные вычисления охватывают широкий спектр методов и алгоритмов, целиком основанных на законах естественной эволюции, предложенных Дарвином. Согласно его законам, лучше всего к жизни в определенной среде подготовлены особи, которые демонстрируют более высокую выживаемость и, как следствие, оставляют больше потомства.

В этой аналогии с законами естественной эволюции особям соответствуют возможные решения задачи. Эволюционные алгоритмы сначала оценивают пригодность каждой «особи», а затем определяют, каким будет их «потомство» — второе поколение решений. В ходе итеративного процесса особи из последующих поколений оцениваются, отбираются и скрещиваются между собой, формируя новые поколения особей. Этот процесс заканчивается после выполнения установленных для задачи критериев останова. Таким образом, любой эволюционный алгоритм состоит из пяти основных этапов: инициализации, оценки, отбора, размножения и замещения, как показано на следующей схеме.

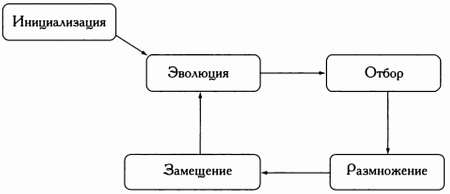
Различия между эволюционными алгоритмами определяются тем, как именно реализован каждый из этих основных этапов.

* * *

ДАРВИН И ЛАМАРК: ДВА РАЗНЫХ ВЗГЛЯДА НА ЭВОЛЮЦИЮ

Жан Батист Пьер Антуан де Моне Ламарк (1744–1829) — французский натуралист, который совершил революцию в биологии, предложив классификацию живых организмов в зависимости от их сложности, а также четко разделив органический и неорганический мир. Еще одним его вкладом в науку стало создание первой биологической теории эволюции, изложенной в книге «Философия зоологии», которая была опубликована в 1809 году, за 50 лет до того, как свою теорию эволюции предложил Дарвин.

Теория Ламарка, в отличие от дарвиновской, основывается на наследовании приобретенных признаков, то есть на способности отдельных особей передавать потомкам приобретенные на протяжении жизни полезные признаки, которые способствуют адаптации к окружающей среде. Различия между теориями эволюции Ламарка и Дарвина прекрасно демонстрирует их объяснение длинной шеи жирафа. Согласно Ламарку, жирафы, которые выше всех вытягивали шею и развивали мышцы, чтобы дотянуться до съедобных листьев на высоких ветках деревьев, передавали этот признак своему потомству, которое продолжало развивать эти мышцы, и в конце концов шеи жирафов достигли нынешних размеров. Согласно теории Дарвина, напротив, жираф, родившийся с самой длинной шеей или с более мощными мышцами, передаст эти признаки потомству независимо оттого, какие усилия он предпринимал при жизни.

Хотя гипотезы Ламарка были отвергнуты в пользу теории Дарвина, не так давно их правильность была подтверждена для некоторых частных случаев. К примеру, известно, что мать, организм которой после пережитой болезни выработал особые антитела, может передать их детям, которые получат иммунитет к этой болезни. Таким образом, здесь мы имеем дело с наследованием признаков, приобретенных при жизни в результате адаптации к окружающей среде.

Карикатура на Ламарка, изображенного в виде жирафа.

Инициализация

Инициализация популяции — отдельный этап, достаточно независимый от используемого эволюционного алгоритма. Инициализация определяется скорее особенностями рассматриваемой задачи — присутствием в ней ограничений, которые следует учитывать, или, напротив, полным отсутствием представления о том, как должно выглядеть «хорошее» решение, в результате чего инициализация выполняется абсолютно случайным образом. Существуют задачи, в которых случайная инициализация предпочтительнее, однако особи первого поколения должны обладать определенными различиями, чтобы охватить все возможные решения.

На этом этапе особенно важно представление знаний об особи, так как оно в значительной степени определит оставшуюся часть эволюционного алгоритма.

Чаще всего особи представляются в виде хромосом. Это новое понятие заимствовано у природы: хромосома представляет собой последовательность генов, а каждый ген — число, обозначающее часть решения.

Рассмотрим в качестве примера алгоритм, цель которого — увеличение емкости картонной коробки при наименьшем расходе картона на ее изготовление. Если мы используем эволюционный алгоритм, то хромосомы, посредством которых мы представим решение, будут иметь три гена: длину, ширину и высоту. При инициализации будет создана популяция коробок произвольных размеров, представленных в виде троек чисел, заключенных в допустимых интервалах. В ходе работы алгоритма популяции коробок будут эволюционировать до тех пор, пока не будет найдена оптимальная коробка в соответствии с установленными критериями.

Оценка

Следующий этап после инициализации — оценка. Обычно считается, что это важнейшая часть эволюционного алгоритма, так как именно она определяет задачу, которую требуется решить. На первом шаге оценки воссоздается решение: информация из хромосомы (генотипа) каждой особи используется для моделирования решения (фенотипа), представленного особью. Целью оценки может быть как простое вычисление объема картонной коробки по известным размерам, как в нашем примере, так и чрезвычайно сложные и дорогостоящие расчеты, к примеру моделирование жесткости конструкции при проектировании моста.

После воссоздания фенотипа необходимо оценить полученное решение. Каждой особи присваивается свое значение приспособленности, которое на последующих этапах эволюционного алгоритма поможет отличить хорошие решения от плохих.

Оценка фенотипов может быть сложной, дорогостоящей и даже зашумленной.

Иными словами, при решении некоторых сложных задач приспособленность одного и того же фенотипа при разных оценках будет различаться. Шум, который также можно назвать ошибкой, неизменно присутствует в задачах, в которых оценка приспособленности используется для численного моделирования. К примеру, при моделировании сопротивления усталости металлов, из которых изготавливаются детали двигателей внутреннего сгорания, решение математических уравнений, описывающих усталость металла, оказывается столь дорогостоящим, что моделирование более выгодно. При этом вполне возможно, что результаты повторного моделирования для каждой детали будут отличаться.

Использование генетических алгоритмов для проектирования деталей двигателей внутреннего сгорания, осуществленное компанией Honda в 2004 году, показало: процесс оценки отличался высоким уровнем шума и неточностью, а также был весьма длительным — расчет приспособленности для каждой особи в популяции занимал восемь часов.

* * *

УПИТАННЫЕ ПТИЦЫ С ОСТРОВА МАВРИКИЙ И ДАВЛЕНИЕ ОТБОРА

Когда исследователи в XVII веке впервые прибыли на остров Маврикий, они обнаружили неожиданный дар небес — упитанных птиц с вкусным мясом, которых стали называть додо. Крылья этих птиц были слишком маленькими, а лапы — слишком короткими, поэтому они не могли ни улететь, ни убежать от охотников. Исследователи безжалостно охотились на додо, а кошки, собаки, крысы и другие животные, завезенные человеком на остров, разоряли гнезда птиц и питались их яйцами.

Додо полностью вымерли менее чем за сто лет, и сегодня эти милые и безобидные птицы известны нам только по рисункам и гравюрам. Додо никогда не испытывали необходимости эволюционировать, а когда они столкнулись с давлением отбора, птицам попросту не хватило времени на то, чтобы справиться с ним. Давление отбора — движущая сила эволюции. Без него живые существа не имеют достаточно стимулов для того, чтобы приспособиться к среде, они не испытывают необходимости развивать оптимальное поведение или другие признаки. В разные годы естествоиспытатели документально описали различные виды, которые, очевидно, находились в похожей ситуации: они обитали в среде, изобиловавшей пропитанием, где отсутствовали хищники, а межвидовая конкуренция была слабой.

Все эти факторы препятствовали появлению признаков, которые были присущи похожим видам, обитавшим в более конкурентных средах.

В отсутствие хищников и при избытке пропитания в изолированной экосистеме острова додо не нужны были сильные крылья и мощные лапы. Кстати, в дословном переводе с португальского «додо» означает «глупый». Кто знает, возможно, додо стали «глупыми» именно из-за того, что отсутствовало давление отбора?

Додо на гравюре XVII века.

Отбор

Следующий этап эволюционного алгоритма, выполняемый после оценки особей текущего поколения, — это отбор. Его цель — выделить лучших особей, которые оставят потомство. Процесс отбора лучших особей является основой естественной эволюции. Интенсивность этого процесса называется давлением отбора. Давление отбора тем больше, чем меньше доля особей, переходящих в следующее поколение.

Однако можно доказать, что если мы применим столь простую стратегию, как прямой отбор лучших особей, то давление отбора будет слишком велико. При значительном давлении отбора эволюционные алгоритмы обычно работают не слишком хорошо, так как завершают работу на локальных, а не глобальных оптимумах.

Главное преимущество эволюционных алгоритмов — возможность получить хорошие решения на больших областях поиска, или, говоря математическим языком, возможность найти оптимумы функций, как правило, многомерных и имеющих несколько локальных или глобальных максимумов. Если давление отбора при эволюционной оптимизации слишком велико, то есть если мы хотим найти решение слишком быстро, для чего выберем лучших особей и ограничимся поверхностным рассмотрением, то алгоритм завершит работу слишком рано, а его результатами будут локальные, а не глобальные оптимумы.

Этап отбора идеально подходит для моделирования давления отбора в эволюционных алгоритмах. В пределе, когда давление отбора будет наибольшим, производится единичный отбор — иными словами, из текущего поколения выбирается только одна особь, на основе которой образуется следующее поколение. Другим предельным случаем будет полностью случайный отбор, при котором приспособленность особей не учитывается. Логично, что следует выбрать некую промежуточную стратегию, при которой производится отбор лучших особей для размножения и вместе с тем присутствует некоторая степень случайности, позволяющая рассмотреть альтернативные варианты. При такой стратегии с определенной вероятностью может быть выбрана любая, даже самая неприспособленная особь. Сегодня применяются три стратегии отбора, обладающие этими свойствами: рулетка, ранговая селекция и турнирная селекция.

Метод селекции, основанный на принципе колеса рулетки, достаточно прост. Он заключается в том, что каждая особь может быть выбрана с вероятностью, пропорциональной ее приспособленности по отношению к приспособленности остальных особей. Следовательно, если нужно отобрать 10 особей, колесо рулетки потребуется вращать 10 раз.

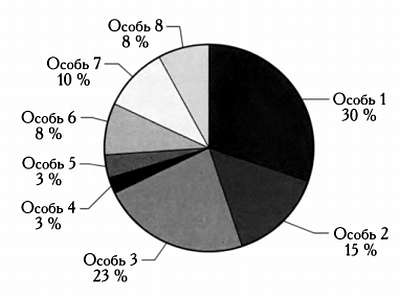
В примере на рисунке представлено восемь особей и значения их функции приспособленности в процентах от целого. Как вы можете догадаться, при каждом вращении рулетки вероятность выбора определенной особи будет пропорциональной отношению ее значения функции приспособленности к целому. Метод рулетки не исключает возможность выбора менее приспособленных особей — они всего лишь будут выбираться с меньшей вероятностью. Если мы будем вращать колесо рулетки 10 раз, то несколько раз обязательно выберем приспособленных особей, но также вероятно, что несколько раз выбранные особи будут не самыми конкурентоспособными. Именно возможность выбора неконкурентоспособных особей делает генетические алгоритмы столь мощными: это позволяет следовать несколькими путями одновременно, открывать другие варианты, выявлять множество различных максимумов, а в долгосрочной перспективе — находить хорошее локальное решение, а в лучшем случае — глобальный максимум.

Еще одна стратегия отбора, пригодная для решения сложных задач, — это ранговая селекция. При ее использовании отбирается n копий наиболее приспособленной особи, n — 1 — второй по порядку и так далее до n = 0. Эта стратегия исключает вероятность того, что некая «сверхособь» снизит вероятность отбора прочих особей.

(«Сверхособью» называется особь, далекая от оптимальной, но намного превышающая по своим параметрам прочих особей из своего поколения.) Наличие сверхособей приводит к тому, что популяция оказывается скученной возле нее, и улучшить результаты становится невозможно.

Третья стратегия, турнирная селекция, заняла монопольное положение среди стратегий отбора, используемых при решении реальных задач, благодаря выгодным математическим свойствам и высокой гибкости при моделировании давления отбора. При турнирной селекции используется тот же принцип, что и при объединении спортивных команд в пары при игре на выбывание. Особи отбираются попарно случайным образом, и оптимальной считается та особь, которая побеждает в этом воображаемом турнире. Следовательно, при турнирной селекции необходимо отобрать столько пар, сколько особей необходимо выбрать. Почему эта стратегия считается очень гибкой при моделировании давления отбора? Что произойдет, если мы будем организовывать «турниры» не между двумя, а между n особями? Что если в турнире будет одерживать верх не одна, а m особей? В таком случае говорят, что проводится турнир n: m. С увеличением n давление отбора будет повышаться, с увеличением m — понижаться.

Чтобы лучше понять схему проведения турнира, представьте себе начальные этапы футбольной Лиги чемпионов. Они проводятся по схеме 4:2 — футбольные команды объединяются произвольным образом в группы по четыре, а две лучшие переходят в следующий этап. Конечно, в примере с Лигой чемпионов нельзя говорить о действительно случайном турнире, так как при формировании групп учитываются определенные критерии — так, в одну группу не могут попасть две команды из одной страны. Однако мы тоже можем вводить свои правила при использовании эволюционных алгоритмов, что будет определять тот или иной тип эволюции.

Часто используется правило, согласно которому в одном турнире соперничают максимально похожие особи. Алгоритм способен находить оптимальные значения функции со множеством оптимумов.

Эти роботы-крабы определяют участки с максимальной освещенностью. У одного из этих роботов нет ног, у другого их сразу четыре. Создатель роботов, Джош Бонгард из Вермонтского университета, описал их поведение с помощью эволюционного генетического алгоритма и смог показать, что они действовали лучше, чем классические роботы, созданные с той же целью.

Размножение

После отбора особей, которые оставят потомство, наступает этап размножения.

Существует несколько систем размножения, которые необязательно являются важнейшими составляющими эволюционных алгоритмов, но на самом деле конкретный эволюционный алгоритм получает свое название в зависимости от того, какая система размножения в нем используется. К примеру, генетические алгоритмы, о которых мы поговорим чуть позже, представляют собой эволюционные алгоритмы, в которых для размножения особей применяется скрещивание с мутациями.

Генетические алгоритмы — самые популярные среди всех эволюционных алгоритмов благодаря тому, что они оптимально сочетают сравнительно невысокую сложность программирования и хорошие результаты. Размножение путем скрещивания с мутациями тесно связано с основными понятиями генетики. В генетическом алгоритме каждая особь представлена хромосомой, а каждая хромосома представляет собой последовательность генов. При скрещивании хромосом двух особей сначала случайным образом определяется точка, которая делит хромосомы на две половины.

Далее эти четыре половины (две для каждой из родительских особей) скрещиваются между собой, и образуется два потомка. Первый потомок содержит первую половину хромосомы первой родительской особи (назовем ее отцом) и вторую половину хромосомы второго родителя (матери). Второй потомок будет содержать первую половину хромосомы матери (до точки пересечения) и вторую половину хромосомы отца.

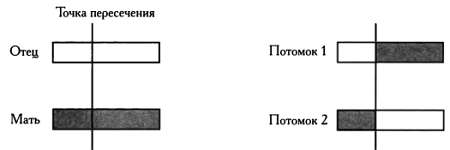
После получения потомства проводится мутация, при которой с очень маленькой вероятностью (как правило, около 5 %) несколько генов в новых хромосомах изменяются случайным образом. В теории и на практике можно показать, что без мутаций генетические алгоритмы не слишком способствуют оптимизации — результатами их работы обычно становятся субоптимумы функции, то есть локальные максимумы. Благодаря мутациям генетические алгоритмы совершают небольшие случайные прыжки в пространстве поиска. Если результаты этих прыжков окажутся не слишком многообещающими, то в ходе эволюции они будут отброшены, в противном случае — закрепятся в наиболее приспособленных особях следующих поколений.

* * *

ГРЕГОР МЕНДЕЛЬ И ГЕНЕТИКА

Австрийский монах Грегор Мендель (1822–1884) открыл и в 1866 году опубликовал первые законы наследования. Эти законы, открытые по результатам скрещивания нескольких видов гороха и известные сегодня как законы Менделя, описывают передачу определенных признаков от родителей к потомкам. С открытием этих законов в генетике и науке вообще появилось важное понятие — доминантные и рецессивные гены.

Мендель в ходе своих экспериментов зафиксировал окрас горошин у различных видов гороха. Первое поколение он получил путем скрещивания растений, приносивших желтые горошины, с растениями, приносившими зеленые горошины. Мендель заметил, что растения, полученные в результате скрещивания, имеют только желтые горошины. Но позднее он обнаружил, что при скрещивании этих растений между собой растения следующего поколения в большинстве своем имеют желтые горошины, однако, к удивлению ученого, у некоторых растений горошины вновь имели зеленый цвет. Соотношение растений с желтыми и зелеными горошинами равнялось 3:1. Проведя аналогичные эксперименты для других признаков, Мендель пришел к выводу: существуют гены, которые доминируют над другими и тем самым подавляют их проявление.

Существование доминантных и рецессивных генов объясняло, почему скрещивание особей с одним и тем же выраженным геном может давать потомство с другим выраженным геном — оба родителя являются носителями рецессивного гена, который подавляется доминантным. Несмотря на то что в свое время труды Менделя не получили широкой известности, в них были заложены основы генетики — науки, которая сыграла определяющую роль в развитии современной медицины.

Замещение

Завершающий этап эволюционного цикла — замещение. Его цель — выбрать, какие особи из предыдущего поколения будут замещены новыми, полученными на этапе размножения. Чаще всего заменяются все особи из предыдущего поколения, за исключением лучшей, которой дается возможность «прожить» еще одно поколение. Этот метод, известный как элитизм, несмотря на крайнюю простоту и некоторую неестественность, оказался удивительно эффективным.

Также было предложено множество других стратегий замещения особей. Обратите внимание, что вновь, как и на этапе отбора, можно смоделировать то или иное давление отбора в зависимости от того, как будут выбираться особи для замещения.

Если мы всегда будем выбирать всех особей популяции и замещать их новыми, давление отбора будет отсутствовать. А если мы будем отбирать только неприспособленных особей популяции для замещения, то давление отбора крайне возрастет.

С другой стороны, на этом этапе также эффективны политики видообразования, то есть методы, упрощающие определение различных решений для задач с несколькими оптимумами. Наиболее популярным среди таких методов является метод замещения посредством цитирования (niching). Суть его состоит в том, что для каждой новой полученной особи производится отбор особей предыдущего поколения, сильнее всего схожих с ней. В следующее поколение переходит только лучшая из этой группы схожих особей.

Мы рассказали о некоторых наиболее популярных методах, применяемых на каждом из этапов эволюционных алгоритмов. Следует понимать, что существует и множество других методов.

* * *

ЭВОЛЮЦИОННЫЕ АЛГОРИТМЫ ЛАМАРКА

Двойственность теорий Дарвина и теорий Ламарка проявляется и в эволюционных алгоритмах.

Отметим, что обе теории оказались крайне эффективными для решения задач оптимизации. Чаще всего используются дарвиновские эволюционные алгоритмы, описанные в этой главе, а алгоритмы, созданные согласно теориям Ламарка, содержат дополнительный этап между оценкой и отбором. Этот этап заключается в краткой локальной оптимизации, имитирующей обучение или адаптацию особи к окружающей среде перед достижением репродуктивного возраста.

Локальная оптимизация, как правило, представляет собой небольшие мутации, применяемые к каждой особи. После мутации оценивается изменение приспособленности. Если приспособленность повысилась, мутация подтверждается, и цикл «мутация-оценка» повторяется вновь.

Если же мутация привела к снижению приспособленности особи, она отвергается, после чего цикл «мутация-оценка» повторяется начиная с состояния, предшествовавшего мутации. Первые эволюционные алгоритмы, построенные согласно теории Ламарка, получили название эволюционных стратегий. Как мы уже упоминали, они использовались немецкими инженерами во время Второй мировой войны для оптимизации сопл двигателей первых реактивных самолетов.

Практический пример: поиск эффективного лекарства

Как вы уже увидели, используя методы оптимизации, основанные на природных процессах, ученые добились огромных успехов в области искусственного интеллекта. Не так давно эволюционные вычисления при изготовлении лекарств позволили добиться заметных успехов. Напомним, что при создании медикаментов целью исследователей является подбор соединения, для которого энергия связи с определенным белком будет отрицательной и минимально возможной. Искомое соединение должно сформировать внутри нашего организма неразрывную связь с белком-мишенью, чтобы их неодолимо тянуло друг к другу, как сладкоежек тянет к карамели.

Рассмотрим, как действует эволюционный алгоритм при оптимизации молекул во время разработки лекарств. Сначала требуется инициализировать популяцию молекул. На этом этапе молекулы обычно формируются случайным образом. Для простоты будем рассматривать поколения всего из трех молекул, хотя обычно их число в одном поколении достигает нескольких сотен.

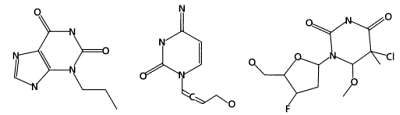
Далее произведем оценку молекул, рассчитав энергию взаимодействия каждой из них с белком-мишенью. Для этого используются различные вычислительные методы. Один из них (мы не будем подробно описывать принцип его действия) называется молекулярным докингом — это трехмерное моделирование, в ходе которого оценивается, сможет ли молекула образовать связь при встрече с мишенью и какой будет энергия этой связи. Возникает любопытная ситуация: при использовании эволюционного алгоритма для поиска идеальной молекулы на одном из его этапов мы вновь применяем эволюционный алгоритм, чтобы оценить качество молекулы по сравнению с остальными. Результатом докинга являются оцененные молекулы.

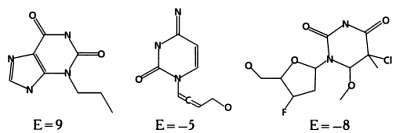
Следующий этап — отбор, который можно организовать, например, путем турнирной селекции. В ходе турнирной селекции случайным образом формируются пары молекул, после чего производится оценка их энергии взаимодействия и принимается решение о том, какие молекулы останутся, а какие — отсеются. Напомним, что энергия взаимодействия должна быть отрицательной и принимать минимально возможное значение.

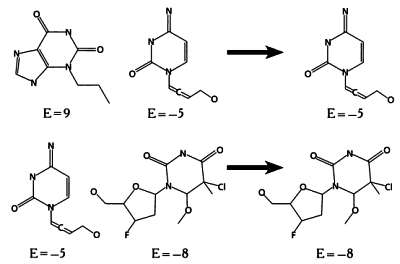
Следующий этап эволюционного алгоритма — размножение, в ходе которого на основе отобранных молекул создаются новые, сочетающие в себе свойства молекул предыдущего поколения. Так, путем скрещивания двух молекул, отобранных на предыдущем шаге, создаются две новые молекулы.

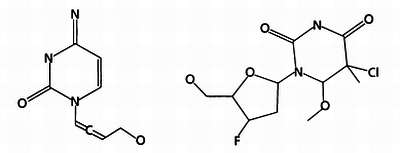
На следующей иллюстрации показано, как две молекулы делятся.

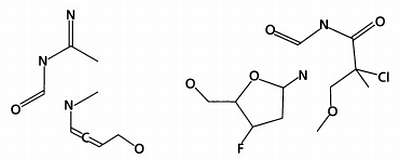
И, наконец, путем соединения частей этих молекул образуются две новые молекулы.

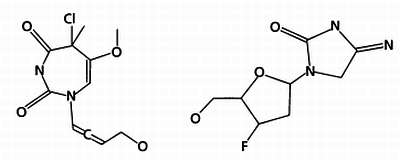
На этапе замещения особи первого поколения замещаются новыми, созданными на предыдущем этапе. Наиболее популярный и простой метод замещения — элитизм, при котором замещаются все молекулы предыдущего поколения за исключением одной, наиболее приспособленной. В нашем случае новое поколение будет состоять из двух молекул, полученных в результате скрещивания, и одной молекулы из предыдущего поколения с энергией взаимодействия, равной —8.

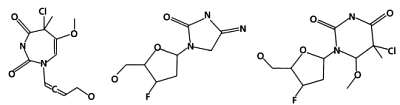
После замещения эволюционный цикл завершается и повторяется необходимое число раз. Иными словами, дальше производится оценка молекул второго поколения, затем среди них отбираются лучшие, и так далее, после чего формируется третье поколение молекул. Процесс повторяется, пока не будет достигнуто заранее определенное число поколений или популяция не сойдется, то есть 90 % особей не будут представлять собой одну и ту же молекулу.

Разумеется, мы приводим упрощенное описание процесса, а в действительности все обстоит намного сложнее. Но скажите, разве сам процесс не прекрасен?